油水砂多相流中固体颗粒对弯管及T型堵头管的冲蚀

彭文山,曹学文,吉俊毅,靳学堂,王 庆

(中国石油大学(华东) 储运与建筑工程学院,青岛 266580)



油水砂多相流中固体颗粒对弯管及T型堵头管的冲蚀

彭文山,曹学文,吉俊毅,靳学堂,王 庆

(中国石油大学(华东) 储运与建筑工程学院,青岛 266580)

摘要：采用计算流体动力学方法在欧拉坐标系下求解连续相运动方程，在拉格朗日坐标系下求解离散相颗粒轨道方程，并利用冲蚀方程研究了管内油、水、砂多相流中固体颗粒运动与管道冲蚀的相互关系，预测最大冲蚀发生位置。结果表明：弯管冲蚀最严重处位于下游直管段与弯头连接处外侧，T型堵头管冲蚀最严重处位于上下游直管段交接处内侧，T型堵头管的最大冲蚀速率远大于弯管的；T型堵头管中存在明显的颗粒相互碰撞区域以及颗粒滞留区域，在颗粒相互碰撞区域颗粒对管壁的碰撞能降低，在颗粒滞留区域颗粒的滞留减少了新来颗粒对堵头的碰撞，这两个区域都从一定程度上减小了颗粒对管道的冲蚀作用。

关键词：弯管；T型堵头管；油水砂；多相流；冲刷腐蚀；颗粒轨迹

在油气田开发过程中，随着开采深度增加以及开采时间的延长，油井出砂量以及原油含水量急剧增加，在油田生产过程中，固体颗粒虽然经过过滤，但是仍然会存在于油水中，砂粒随着油水混合液一起流动，严重磨损管道内壁，由于油气集输是一个连续的过程[1]，砂粒对于管道内壁的冲蚀也持续进行，直到管壁出现破损。弯管和T型堵头管是管道系统中改变流体流动方向的常用管件，当流体中含有的固体颗粒时，固体颗粒会随着流体流动与管件壁面发生碰撞，因此该处特别容易遭受冲蚀磨损。在实际工程中，特别是在易发生气固两相流冲蚀的工程中，在不允许使用大曲率弯管的情况下，T型堵头管常被用来替换大曲率弯管[2]，因此，研究弯管和T型堵头管的冲蚀行为对于保证管道完整性以及提高输运系统的经济性具有重要意义。

目前,关于油水两相流动方面的研究较多[3-6]，如油水两相流压降、流型及油水两相分布等规律。在弯管和T型堵头管冲蚀方面，部分学者对气固/液固两相的冲蚀进行了研究。Bourgoyne[7]建立了输送系统模型,并分析了固体颗粒对标准弯头、T型堵头管等不同管件的冲蚀作用，利用超声波测定管件的厚度损失，评价不同管件的抗冲蚀能力。Chen等[8]试验研究了标准弯头和T型堵头管不同部位的冲蚀情况，采用表面光度仪通过刻划基准面来标定试验前后的试件轮廓，以此来计算材料的厚度损失，评价冲蚀作用。但以上研究均针对气砂或者水砂两相，对油水砂多相流的冲蚀并未进行过分析。关于油水砂多相流冲刷腐蚀鲜有报道，且这些研究主要集中在油水混合液中管道腐蚀产物的测定[9]、电化学腐蚀与冲蚀交互作用[10]、油水乳状液的电化学腐蚀电位测量[11]方面。传统的油水两相流试验是在室内搭建试验环路，配制油水混合液，改变不同参数，用拍照方式观察管内流动;而对于含固体颗粒的管流冲刷试验则需搭建管流试验装置，改变不同冲刷参数，利用丝束电极技术来完成管件局部冲蚀的检测[12-13]。两者要进行结合比较复杂，不仅搭建设备费用高，而且运行周期长，操作也比较复杂。鉴于计算流体动力学(CFD)在处理冲蚀问题上具有准确高效的特点，已经被广泛应用于冲蚀预测，本工作采用计算流体动力学方法结合E/CRC冲蚀模型，计算了弯管及T型堵头管在油水砂多相流中固体颗粒影响下的冲蚀行为，得到管件内部油水两相分布、流场变化以及固体颗粒运动情况与冲蚀速率之间的关系，完成冲蚀预测，找出冲蚀最严重部位，为油气田开发过程中的管件冲蚀预测及管件优化提供参考。

1数学模型

1.1模型选择

管道内为油水砂多相流，连续相主要是油、水两相，由于mixture模型可以较完善地描述将连续相在流道内的分布规律，并且此模型用于模拟相间曳力规律不明显的两相流时更加准确，因此连续相计算选用mixture模型；由于颗粒相的体积分数足够小，可以采用离散相模型(DPM)进行研究；鉴于标准k-ε模型具有适用范围广、精度高的优点，故数值模拟采用标准k-ε湍流模型。

1.2连续相控制方程

(1) 连续方程

(1)

式中:αk为第k相的体积分数；ρk为第k相的密度,kg/m3；vk为第k相的平均速度,m/s。

(2) 动量方程

(2)

式中:p为压力，Pa；τk为分子动力，N/m2；τk′为紊动应力，N/m2；Mk为单位体积相间动量传递，N/m3；(Fint)k为内在力，N/m3；g为重力加速度，m/s2;SD为动量源项，N/m3。

(3) 湍流方程

(3)

其中:

(4)

式中：μt为湍动黏度，Pa·s；k为湍流动能，J；ε为湍流耗散率，W/m3；Gk为由于平均速度梯度引起的湍动能k的产生项；Gb为由于浮力引起的湍动能k的产生项；YM为可压湍流中脉动扩张的贡献；Sk，Sε为自定义参数，无因次；μi为时均速度，m/s；xi，xj为空间坐标，m，i≠j；σk为k方程的湍流Prandtl数，取为1.0；σε为ε方程的湍流Prandtl数，取为1.3；C1ε=1.44，C2ε=1.92，Cμ=0.09为经验常数。

1.3离散相控制方程

DPM模型通过积分Lagrangian坐标系下的离散颗粒的运动方程计算运动轨迹。固体颗粒在两相流中受到绕流阻力、重力、附加质量力、压力梯度力、Basset力、萨夫曼(Saffman)力、马格努斯(Magnus)力等作用力，由颗粒的惯性与受力平衡，分散相颗粒运动方程为：

(5)

式中:u为连续相速度;up为砂粒速度;ρp为砂粒密度;dp为砂粒直径;gy为y方向重力加速度，为-9.81 m/s2;Rep为相对雷诺数;CD为曳力系数;Fy为y方向的其他作用力:包括附加质量力、热泳力、布朗力和Saffman升力等；在一定雷诺数范围内，对于球形颗粒，a1,a2,a3是常数，取值参考文献[14]。

由于流场中固体颗粒的含量较小，连续相的流体速度较大，连续相和离散相之间具有较大的密度差，且固液流场的温度为常温，因此固体颗粒受到的绕流阻力、附加质量力、流场的压力梯度引发的附加力、Basset力、Saffman升力和Magnus升力等作用力都不予考虑[15]。

1.4冲刷腐蚀模型

液固两相流冲刷腐蚀的影响因素很多，包括流体力学因素、材料因素、固相颗粒因素以及液相因素等方面[16]，弯管及T型堵头管的冲蚀主要受到颗粒速度，颗粒流量、颗粒尺寸、冲刷角度、管道材料等因素影响，其中固体颗粒因素对冲蚀影响较为重要，鉴于E/CRC冲蚀模型[17-18]充分考虑了靶材硬度,颗粒碰撞角度与速度等因素以及较广泛的适用范围等优点，将此模型应用到CFD软件中完成冲蚀计算:

(6)

(7)

式中:vER为冲蚀速率，为单位质量颗粒所造成管壁材料质量的损失;C为常数，2.17×10-7;n为速度指数，2.41;HB为管壁材料的布氏硬度，MPa；FS为颗粒形状系数，尖锐颗粒取1.0，完全球形的颗粒取0.2，介于两者之间的取0.53;up为颗粒撞击管壁的速度，m/s;θ为颗粒撞击管壁的角度，rad。

2冲蚀数值模型

2.1弯管及T型堵头管参数

以西江某油田海底管道油水参数建立数值计算模型，弯管模型由3部分组成，分别是进口段、弯头段、出口段。弯管管径D=50 mm，为了使管内流动充分发展，上下游管路长度L1和L2均取18D，弯径比R/D=1.538。T型堵头管管径D=50 mm，上下游管路均为18D，堵头长度L3=1.538D。

管中主相为水，密度为998 kg/m3，动力黏度为1 mPa·s，第二相为中质油，密度为887.3 kg/m3，黏度为27.2 mPa·s，原油体积含水率为40%。离散相砂粒密度为2 650 kg/m3，粒径450 μm，砂粒的质量流速为0.235 kg/s，入口速度为4 m/s，从水平直管入口流入，从竖直向上直管流出。

2.2网格划分

经初步计算，模型内部为湍流流动，湍流流体质点的不规则运动造成质点在主运动之外还有附加的脉动，因此需要更精确地网格划分。普朗特等的研究发现在管道近壁处存在黏性底层，因此考虑黏性底层的影响，网格距离要小于黏性底层的厚度，网格划分时对边界层部分的网格进行了细化，以提高计算精度;另外由于T型堵头管结构不规则，采用非结构化网格处理。网格划分如图1所示。

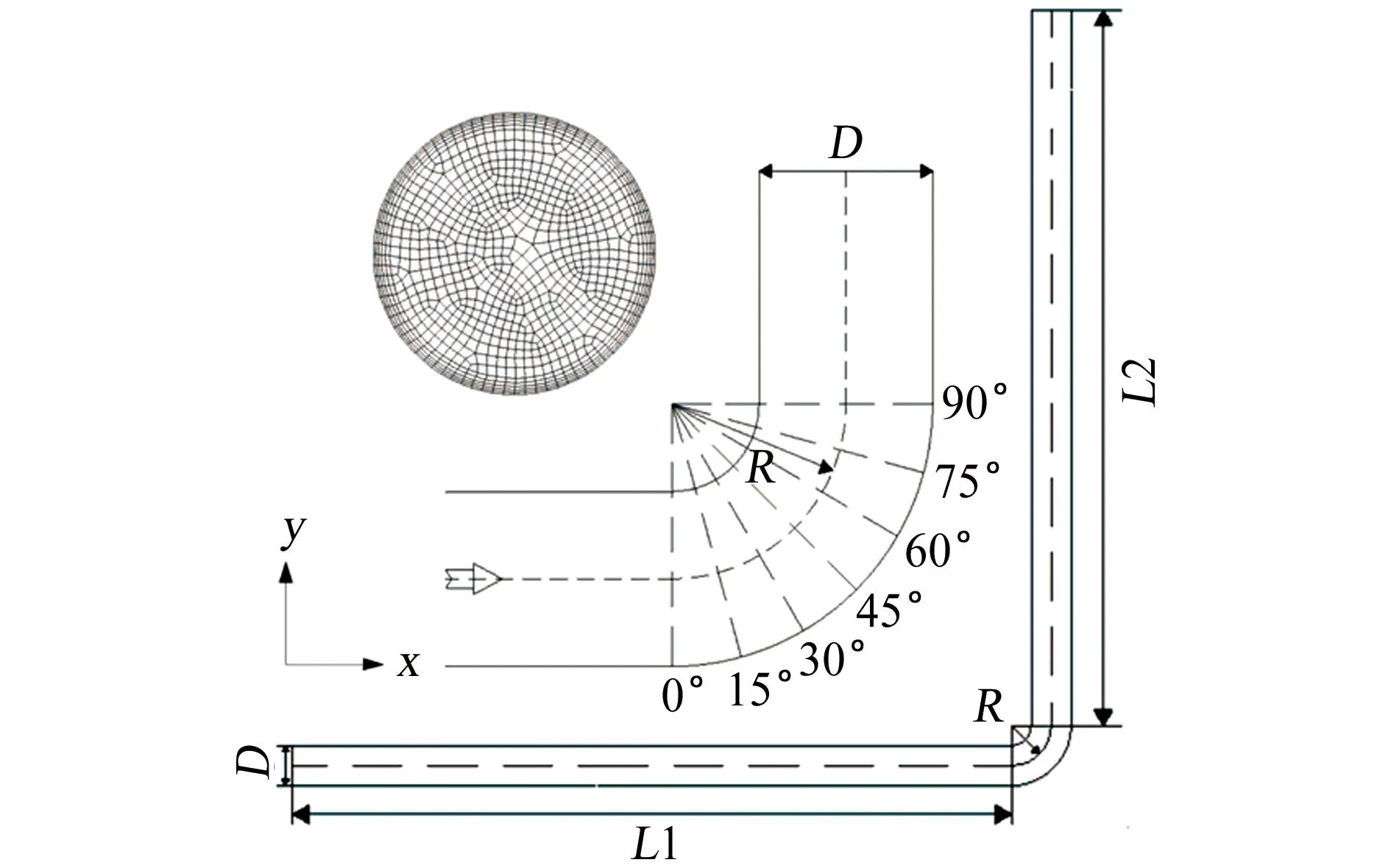
(a)　弯管

(b)　T型堵头管图1　弯管及T型堵头管计算区域几何模型及网格划分Fig. 1　Geometry and grid division of bend pipe (a) and plugged tee (b)

2.3边界条件

连续相：流体计算采用标准k-ε湍流模型，近壁区域采用标准壁面函数处理。入口采用速度进口边界条件，出口为自由出流边界。管壁为壁面边界，壁面粗糙度高度设为10 μm，粗糙度常数设为0.5，湍流描述中湍流强度设为3.5%；并设定壁面边界为静止壁面和无滑移壁面。

离散相：DPM模型中进口和出口处采用逃逸(Escape)条件，壁面采用反弹(Reflect)条件，假设入射的粒子是相互独立，均匀的球形，忽略颗粒之间相互碰撞导致的结合与破碎。需特别说明的是固体颗粒作无旋运动，忽略颗粒与颗粒之间的碰撞[19]，颗粒轨迹采用拉格朗日方程进行求解。颗粒相的射流采用面射流源，从进口边界面上抛撒惯性颗粒，颗粒的初始速度与流体进口速度相同。固体颗粒与壁面发生碰撞时存在能量的转移和损失，主要表现在碰撞前后速度分量的变化。通常以碰撞前后速度分量的比值衡量能量的损失情况，并将该比值定义为恢复系数。比较常用的恢复系数包括Forder[20]提出的Forder恢复系数以及Grant等[21]提出的stochastic 恢复系数。本研究采用在计算中具有较高准确性Forder恢复系数，方程形式为：

(8)

式中：εT,εN分别为切向和法向方向的Forder恢复系数。

2.4数值算法

动量、湍动能的离散均采用二阶迎风格式，体积分数离散采用一阶迎风格式，多相流模型采用mixture混合模型，固体颗粒采用DPM模型，压力速度耦合采用SIMPLE算法。

离散相采用双相耦合计算，计算开始前打开离散相模型加入离散相粒子，初始化流场，设置相间耦合、每5步连续相后进行离散相轨道计算，然后将更新后的离散相动量与能量加入下一步的连续相方程中计算，收敛稳定后，进行离散相后处理和观察连续相流场情况。

3数值计算结果

3.1水相分布

弯管及T型堵头管水相体积分数分布见图2，由图可知，在弯管弯头区域，弯头外侧水相体积分数较大，越靠近弯头内侧水相体积分数越小，且在弯头最内侧达到最小值。这主要是由于当油水混合液流经弯头部位时，离心力的作用使得密度较大的水相更容易流向弯头外侧，造成内侧油相比例较高。在T型堵头管流动方向发生变化的区域，堵头区域以及出口直管段与堵头连接处侧壁的水相体积分数较大，而在入口直管段与出口直管段连接处的内侧，水相体积分数最小。这主要是由于油水混合液由入口流到堵头区域时流动方向迅速发生变化，离心力使得密度较大的水相更容易流向堵头处，而油相在入

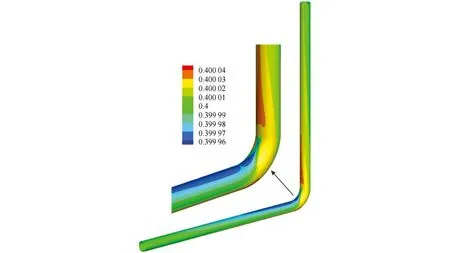
(a)　弯管

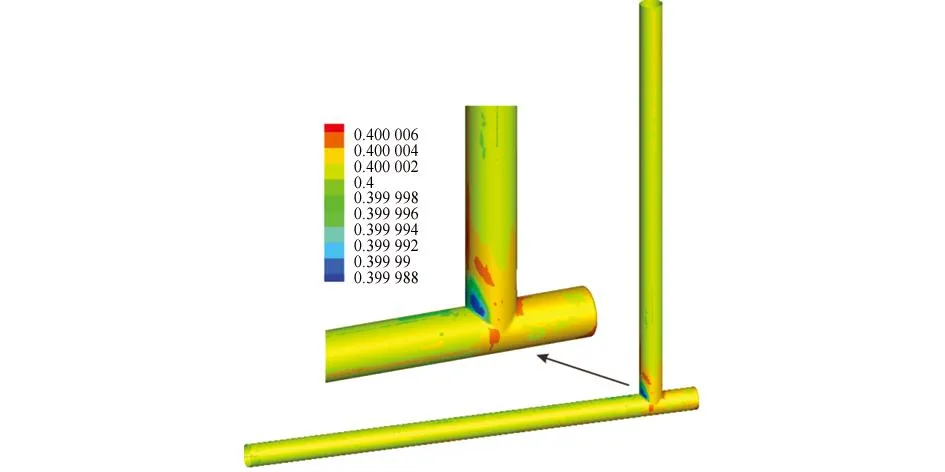
(b)　T型堵头管图2　弯管及T型堵头管水相分布图(体积分数)Fig. 2　The water phase distribution (volume fraction) in pipe bend (a) and plugged tee (b)

口直管段与出口直管段连接处内侧的比例较大。

3.2管内油水两相速度场分布

数值计算发现，在管道弯头处冲蚀速率最大，最易破坏，为深入分析弯管冲蚀速率与管道内部流场之间的关系，选取弯头0°~90°七个截面(见图1)进行分析，T型堵头管冲蚀最严重部位出现在流动方向改变处，因此选取流动方向改变处的P1、P2、P3三个截面(见图1)进行分析，弯管及T型堵头管不同截面处流场分布见图3。

由图3可知，对于弯管，随流动发展，流体在入口直管段流动一定距离后，流速达到最大值，在弯头处，流动方向发生突变，流速分配严重不均，在下游直管段与弯头连接处外侧流速较大，而在弯头内侧流速较小，在下游直管段由于受到弯头处流体运动方向变化的影响，流速在很长一段距离都表现得不均匀，有关文献表明，这种影响会持续50倍管径以上的距离[22]。在弯头处，随着截面角度的增加管中最大流速区域的面积越来越小，且在45°截面左右出现二次流，随角度增加二次流越来越明显。

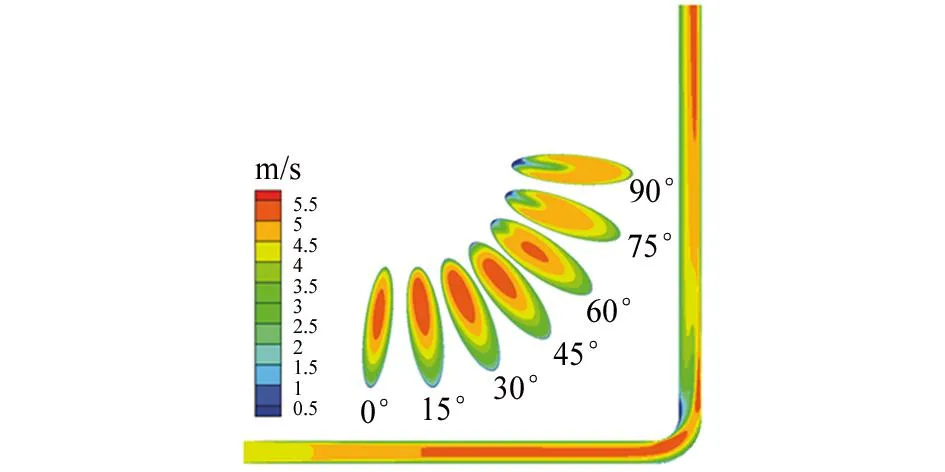
(a)　弯管

(b)　T型堵头管图3　弯管及T型堵头管不同截面处流场分布图Fig. 3Flow field distribution in different sections of pipe bend (a) and plugged tee (b)

对于T型堵头管，在入口直管段流速分布较均匀，在堵头区域由于并无出流条件，因此流速特别小，来流的冲击使得部分流体进入堵头，另有部分流体从堵头向出口直管段流出。在流动方向发生突变的T型交接处，流速产生剧烈变化，在下游直管段与上游直管段连接处外侧流速较大，而内侧流速较小，经过T型连接处后流体在下游直管段中流速逐渐变均匀。在T型连接处，P1截面处最内侧出现最大速度主要是由于在此处流动防线发生90°巨大变化，由于离心力作用使得内侧流速瞬间增大，P2截面处流速较大，区域面积较大，而在P3截面处由于无流动出口，因此整个截面流速很小。

3.3固体颗粒运动轨迹与冲蚀速率

(a)　弯管

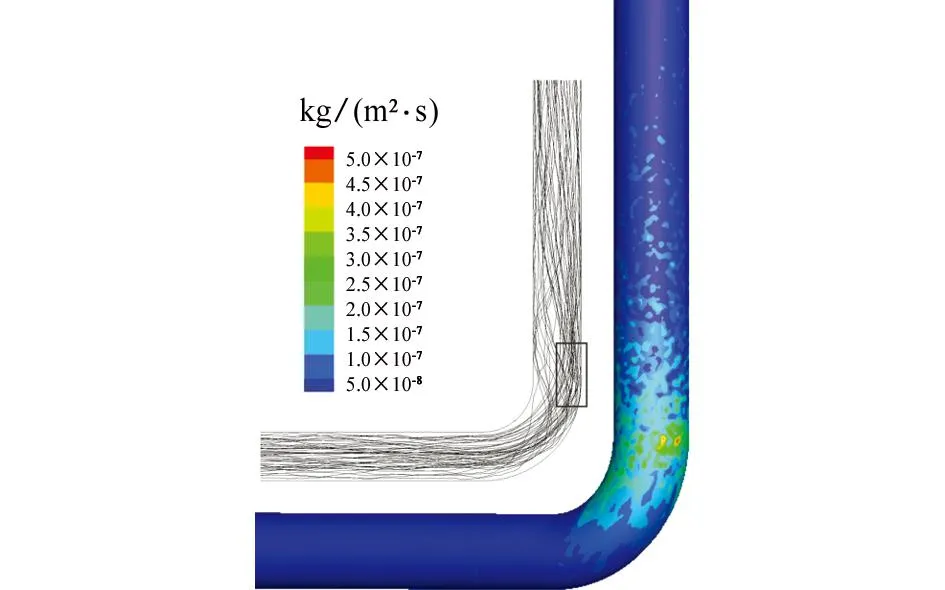
(b)　T型堵头管图4　弯管与T型堵头管颗粒轨迹与冲蚀速率示意图Fig. 4　Particle trajectories and erosion rate schematic diagram of pipe bend (a) and plugged tee (b)

采用拉格朗日方程对颗粒轨迹进行求解，弯管与T型堵头管颗粒轨迹与冲蚀速率见图4。由图4可知，弯管冲蚀严重区域主要出现在下游直管段与弯头连接处外侧，主要是由于固体颗粒斯托克斯数较大，惯性对颗粒的影响明显，颗粒沿着来流方向与下游直管段和弯头连接处碰撞次数较多，另外直管段与弯头连接处流速较大，且此处水相体积分数较大，流体黏度较小，使得颗粒的碰撞能增加，故冲蚀速率较大。对于T型堵头管，冲蚀最严重区域出现在上游直管段与下游直管段连接处内侧壁，从固体颗粒的运动轨迹来看，此处产生较大的冲蚀速率主要是由于此处产生二次流且二次流的合速度方向指向内侧壁，二次流携带固体颗粒对壁面的碰撞能较大，撞击壁面造成冲蚀较严重，另外由于入口直管段中部分颗粒随流体进入堵头区域，与堵头壁面碰撞反弹后撞击到内侧壁，加剧了该区域的冲蚀。

弯管的最大冲蚀速率为5.27×10-7kg/(m2·s)，而T型堵头管最大冲蚀速率达到6.08×10-6kg/(m2·s)，T型堵头管的冲蚀速率是弯管的十几倍，差别较大，这与Chen[2,7]等的研究结果一致。Chen等的研究发现，T型堵头管内部流体流动方向变化更加明显，更多的固体颗粒在惯性作用下冲击管壁，在相同管径和颗粒直径等计算参数条件下，T型堵头管的冲蚀速率几倍于弯头。而Bourgoyne通过试验也发现，液固两相流条件下，大曲率弯管比T型堵头管更耐冲蚀，T型堵头管的冲蚀速率较大。因此在含固体颗粒的油水混输工程中，要慎重选择T型堵头管替换大曲率弯管来改变流体流动方向。

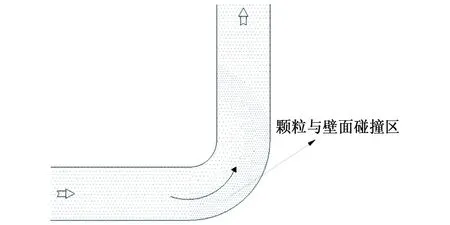
弯管及T型堵头管中颗粒碰撞区及滞留区见图5。由图5可知，在弯管弯头区域，由于流体流动方向的变化较T型堵头管平缓得多，因此颗粒仅在下游直管段与弯头连接处外侧对管壁碰撞次数较多，且该处的流速较大，因而在弯头外侧区域冲蚀速率较大。在T型管堵头区域，流场较为复杂;一部分颗粒将滞留在堵头区域，对堵头壁面形成了保护，而且在上下游直管交界处，另一部分颗粒从堵头区流出,与入口流入的颗粒发生对撞消能，颗粒撞击管壁的数目和速度均降低，因此该区域的冲蚀速率较小。

(a)　弯管

(b)　T型堵头管图5　弯管及T型堵头管中颗粒碰撞区及滞留区示意图Fig. 5　Schematic of particle collision area and particle retention area in pipe bend (a) and plugged tee (b)

4结论

(1) 弯管的最大冲蚀位置出现在下游直管段与弯头连接处，T型堵头管的最大冲蚀位置出现在上游直管段与下游直管段连接处内侧， 在相同的流动环境中，T型堵头管的最大冲蚀速率远大于弯管，在油水混输过程中进行T型管替换弯管时要特别重视。

(2) 固体颗粒在弯管的弯头外侧存在颗粒碰撞区，在此区域固体颗粒与管壁的碰撞次数较多且速度较大，固体颗粒在T型堵头管内存在颗粒相互碰撞区以及颗粒滞留区，在颗粒相互碰撞区由于固体颗粒相向运动造成颗粒碰撞，颗粒对管壁的碰撞能减小，而在颗粒滞留区由于颗粒聚集在堵头末端，减小了后来的颗粒对堵头的碰撞频率，一定程度上保护了堵头末端区域。

参考文献：

[1]王思邈，刘海笑，张日，等. 海底管道沙粒侵蚀的数值模拟及侵蚀公式评价[J]. 海洋工程，2014,32(1)：49-59.

[2]CHEN X H,MCLAURY B S,SHIRAZI S A. Numerical and experimental investigation of the relative erosion severity between plugged tees and elbows in dilute gas/solid two-phase flow[J]. Wear,2006,261:715-729.

[3]BUEL J R,SOLIMAN H M,SIMS G E. Two-phase pressure drop and phase distribution of a horizontal tee junction[J]. International Journal of Multiphase Flow，1998，24：775-792.

[4]PANDEY S，GUPTA A，CHAKRABARTI D P，et al. Liquid-liquid two phase flow through a horizontal T-junction[J]. Chemical Engineering Research & Design，2006，84(10)：895-904.

[5]吴铁军，郭烈锦，刘文红，等. 水平管内油水两相流流型及其转换规律研究[J]. 工程热物理学报，2002，23(4)：491-494.

[6]钟兴福，黄志尧，吕鹏举，等. 125 mm垂直圆管中油水两相流流型辨识研究[J]. 石油学报，2001，22(5)：89-94.

[7]BOURGOYNE A T． Experimental study of erosion in diverter systems due to sand production[C]//Proceedings of the SPE/IADC Drilling Conference. New Orleans:[s.n.],1989:807-816.

[8]CHEN X，MCLAURY B S，SHIRAZI S A． Application and experimental validation of a computational fluid dynamics (CFD)-based erosion prediction model in elbows and plugged tees[J]． Computer and Fluids，2004，33(10):1251-1272.

[9]LIU Y C,ZHAN Y L,YUAN J M,et al. Research on corrosion perforation on pipeline by media of high salinity acidic oil-water mixture[J]. Engineering Failure Analysis,2013,34:35-40.

[10]STACK M M,ABDULRAHMAN G H. Mapping erosion-corrosion of carbon steel in oil-water solutions:effects of velocity and applied potential[J]. Wear.2012,(274/275):401-413.

[11]ZHANG G A,CHENG Y F. Electrochemical corrosion of X65 pipe steel in oil/water emulsion[J]. Corrosion Science,2009,51:901-907.

[12]ZENG L,ZHANG G A,GUO X P,et al. Inhibition effect of thioureidoimidazoline inhibitor for the flow accelerated corrosion of an elbow[J]. Corrosion Science,2015,90:202-215.

[13]ZENG L,ZHANG G A,GUO X P. Erosion-corrosion at different locations of X65 carbon steel elbow[J]. Corrosion Science,2014,85:318-330.

[14]MORSI S A,ALEXANDER A J. An Investigation of particle trajectories in two-phase flow systems[J]. J Fluid Mech,1972,55(2):193-208.

[15]BADR H M,HABIB M A,BEN-MANSOUR R,et al. Numerical investigation of erosion threshold velocity in a pipe with sudden contraction[J]. Computers & Fluids,2005,34(6):721-742.

[16]朱娟,张乔斌,陈宇,等. 冲刷腐蚀的研究现状[J]. 中国腐蚀与防护学报,2014,34(3)：199-210.

[17]ZHANG Y,REUTERFORS E P,MCLAURY B S,et al. Comparison of computed and measured particle velocities and erosion in water and air flows[J]. Wear,2007,263:330-338.

[18]PARIS M,NAJMI K,NAJAFIFARD F,et al. A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications[J]. Journal of Natural Gas Science and Engineering,2014,21:850-873.

[19]SUZUKI M,INABA K,YAMAMOMO M. Numerical simulation of sand erosion in a square-section 90-degree bend[J]. Journal of Fluids Science and Technology,2008,3(7)：868-880.

[20]FORDER A,THEW M,HARRISON D. Numerical investigation of solid particle erosion experienced within oilfield control valves[J]. Wear 1998,216:184-193.

[21]GRANT T,TABAKOFF W. Erosion prediction in turbomachinery resulting from environmental solid particles[J]. J Aircraft,1975,12:471-547.

[22]蔡增基，龙天渝． 流体力学泵与风机[M]． 4版. 北京：中国建筑工业出版社，1999：115-122.

Erosion of Pipe Bend and Plugged Tee by Solid Particles in Oil-Water-Sand Multiphase Flow

PENG Wen-shan, CAO Xue-wen, JI Jun-yi, JIN Xue-tang, WANG Qing

(College of Pipeline and Civil Engineering, China University of Petroleum, Qingdao 266580, China)

Abstract：The method of computational fluid dynamics (CFD) was used to solve continuous phase motion equation in the Euler coordinate system, and to solve the discrete phase particle trajectory equation in the Lagrange coordinate system. Then the erosion equation was used to study the relationship between solid particles and pipe erosion in oil-water-sand multiphase flow, and then the maximum erosion position was predicted. The results show that the most serious erosion region in the bend pipe was in the outermost side of the junction of downstream straight pipe and elbow; however for plugged tee, the region was the inner side of the junction of upstream and downstream straight pipe. And the maximum erosion rate of plugged tee was much higher than that of pipe bend. Particle collision region and particle retention region were found in the plugged tee. In the collision region, the collision energy of particles against pipe wall decreased, while in the retention region, the retention of particles impeded the impacts of new particles against the plugged tee. These two regions reduced erosion rate of plugged tee in a certain extent.

Key words：pipe bend; plugged tee; oil-water-sand; multiphase flow; erosion-corrosion; particle trajectory

中图分类号：TG174

文献标志码：A

文章编号：1005-748X(2016)02-0131-06

通信作者：曹学文(1966-)，教授，博士，从事天然气处理与加工、油气水多相流理论及应用、海底管道完整性管理等方面的研究，15053208836，caoxw@upc.edu.cn

基金项目：国家自然科学基金(51274232)； 中央高校基本科研业务费专项资金资助(15CX06070A)

收稿日期：2015-01-29

DOI:10.11973/fsyfh-201602009