基于S变换样本熵的输电线路纵联保护新原理

吴 浩



基于S变换样本熵的输电线路纵联保护新原理

吴 浩1,2

(1.西南交通大学电气工程学院，四川 成都 610031；2.四川理工学院自动化与电子信息学院，四川 自贡 643000)

提出了一种基于电流行波S变换样本熵的快速纵联保护新方法。利用故障后一段时间内线路两端故障电流行波的S变换样本熵比值来识别区内外故障。区外故障时，一侧的反行波和另一侧前行波为同一行波，波形相似，对应电流行波样本熵基本相同，其比值接近1。区内故障时，线路一侧的反行波和另一侧前行波为不同行波，波形相似度小，线路两端电流行波样本熵差异较大，其样本熵之比(数值小的与数值大的之比)最小。利用此特征可以确定线路区内外故障。仿真结果表明，所提出的纵联保护方案能够快速识别区内外故障，其性能不受故障类型、故障初始角、接地电阻、故障位置和母线结构的影响。

输电线路；纵联保护；故障行波；S变换；样本熵

0 引言

超高压长距离输电线路具备较大导线分裂数、较大分布电容等特点，故障暂态过程有较长的持续时间，暂态量变化较为复杂，不利于传统保护的正确动作[1-2]。目前基于工频量的传统保护性能难以再得到提高[3]，而行波保护因其高速的动作性能和不受系统振荡等因素的影响已经成为继电保护领域研究的热点[4-7]。

文献[8]分析了直流输电线路区内外故障时的行波传输过程，探寻线路两端前行波和反行波的差异，提出基于行波波形相关性的纵联保护新原理。文献[9]研究正反方向线路故障后初始行波的特征，基于S变换和波阻抗提出双阻抗圆的方向判据，形成一种新型波阻抗方向继电器。

近年来，信息熵在电力系统故障检测、故障选相和保护等领域已取得了不少成果[10-12]。文献[13] 对故障后一段时间内故障电压、电流的极性关系利用S变换能量相对熵来表征，根据线路两端S变换能量相对熵的比值来识别区内外故障。文献[14]计算暂态零模电流近似熵，比较区段两端近似熵的比值大小确定小电流接地故障位置。这些研究为信息熵在电力系统保护领域的应用提供了新的思路。

基于此，为最大限度利用故障暂态过程中的电流行波信息，本文在综合现有文献分析故障电流方向行波特点的基础上，结合信息熵理论，利用S变换样本熵来描述一段时间内线路两端前行波和反行波的波形差异，通过计算线路两端电流方向行波样本熵之比确定区内外故障。

1  输电线路故障电流行波特征分析

图1所示的高压输电系统中，CS为母线对地电容，保护单元 R1和 R2分别安装在线路L3的B侧和C侧，R3和R4分别安装在线路L4的C侧和D侧，规定母线指向线路为电流正方向。

图1高压输电系统

以线路L3为例，根据故障叠加原理，线路发生故障时，故障点产生的故障行波向线路两端传播，R1和R2处测量到的电流由2个波速相同、传播方向相反的行波组成。参照规定的正方向，R1处的故障电流前行波和反行波可以表示为[5-7]

由文献[5-6]对电流方向行波的传播特征分析可知，当线路正常运行或区外故障时，有

线路内部发生故障时，行波由故障点向线路两端传播，方向行波之间的折反射关系较为复杂[5-7]，线路两端检测到的方向行波和(和)本质上不是同一行波，即使忽略传播延时，两边的方向行波波形仍然差异很大。附录图A1给出了区外故障时电流方向行波波形，附录图A2给出了区内故障时的电流方向行波波形，仿真实验结果验证了理论分析的正确性。

基于以上分析，本文尝试利用S变换样本熵来刻画区内外故障时线路两端电流方向行波(如和，和)的波形差异，构建新型行波纵联保护。

2 S变换样本熵

2.1样本熵

样本熵(Sample Entropy)从衡量序列复杂性的角度提供了一种表征信号特征的无量纲指标[15]，信号序列越复杂，对应的样本熵值越大。该方法所需数据短，适应于各类确定性信号和随机信号，为电力系统故障诊断和保护算法提供了新的有效特征参数。样本熵的具体算法如下[15-16]。

Step5：序列的样本熵定义为

取有限值时，样本熵的估计值为

2.2 S变换样本熵

S变换是类似于短时傅里叶变换的时频变换方法，能对信号实现时频联合分析[17]。设信号的离散时间序列为：,其中为采样间隔。则序列的离散傅里叶变换可以表示为[17-19]

3  基于S变换样本熵的纵联保护算法

3.1 保护判据推导

根据上文分析结果可知，输电线路区内故障时，线路一侧的故障电流前行波和另一侧的故障电流反行波属于不同行波，波形差异很大，波形相似度很低，两侧电流方向行波S变换样本熵数值差异也随之较大，样本熵的比值较小(样本熵数值小的与数值大的之比)。区外故障时，如式(2)所示，线路一侧的反行波是由另一侧的前行波传播而来，本质上属于同一行波，波形高度相似。在各自初始波头到达测量端后一段时间内，两端电流方向行波S变换样本熵基本相同，其比值接近1。

因此利用线路两侧故障电流方向行波的S变换样本熵之比作为保护判据，能够很好体现线路内外故障时的差异特征。对图1线路L3的保护而言，分别计算线路B端电流反行波S变换样本熵和前行波S变换样本熵，线路C端电流反行波S变换样本熵和前行波S变换样本熵，令

具体保护判据为

若满足判据(15)，判定线路区内故障，若样本熵比值均大于，则判定为区外故障。考虑到区内不同类型故障时电流行波及S变换样本熵的差异性特点，选择保护判据门槛值为0.8，后文将利用大量仿真实验验证该门槛值选择的合理性。

3.2 保护方案实现步骤

实际三相线路存在电磁耦合，三相电压电流量不能直接利用，本文根据CLARK相模变换方法对三相线路进行解耦处理，得到三相相互独立的电流、电压行波模分量：。

单独采用一种模量分析可能导致某些故障下没有暂态行波分量，保护可能失灵，为了提高保护的灵敏度和可靠性，本文采用组合模量法[20]。

电流组合模量：

电压组合模量：

由式(16)、式(17)得到行波组合模量，再根据式(1)计算故障电流前行波和反行波，对研究线路端选定的前行波或反行波进行S变换，得到方向行波的S变换模量矩阵。经过大量的仿真实验分析，选择20 kHz所对应的单频率故障电流方向行波计算S变换样本熵，能很好反映方向行波波形复杂程度。

在本文的保护方案中，对于区外故障，近故障点侧前行波与远故障点侧反行波(或近故障点侧反行波与远故障点侧前行波)本质上为同一行波，波形相似，对应样本熵值几乎一样，差异很小。但是行波在线路上传播存在延时，造成线路两端测量到的行波不同步，会削弱这种近似特征。

因此本文对线路两端的电流方向行波进行S变换，在确定用于样本熵计算的特定频率条件下，选择各端单频率故障行波S变换初始模极大值对应时刻，作为两端保护计算所用对应数据的采集起始时刻。对区外故障而言，线路两端各自故障电流方向行波S变换初始模极大值对应时刻开始的一段时间内，采集到的时间序列本质上是消除传播延时后的同一序列，提高了保护的可靠性。在区内故障时，用于计算样本熵的对应方向行波本质上为不同行波，波形数据是否同步不会改变这种特征，因此，本文选择的数据采集起始时刻对区内故障判别效果不造成影响。

综上分析，利用电流方向行波S变换样本熵构成的纵联保护算法流程如图2所示。

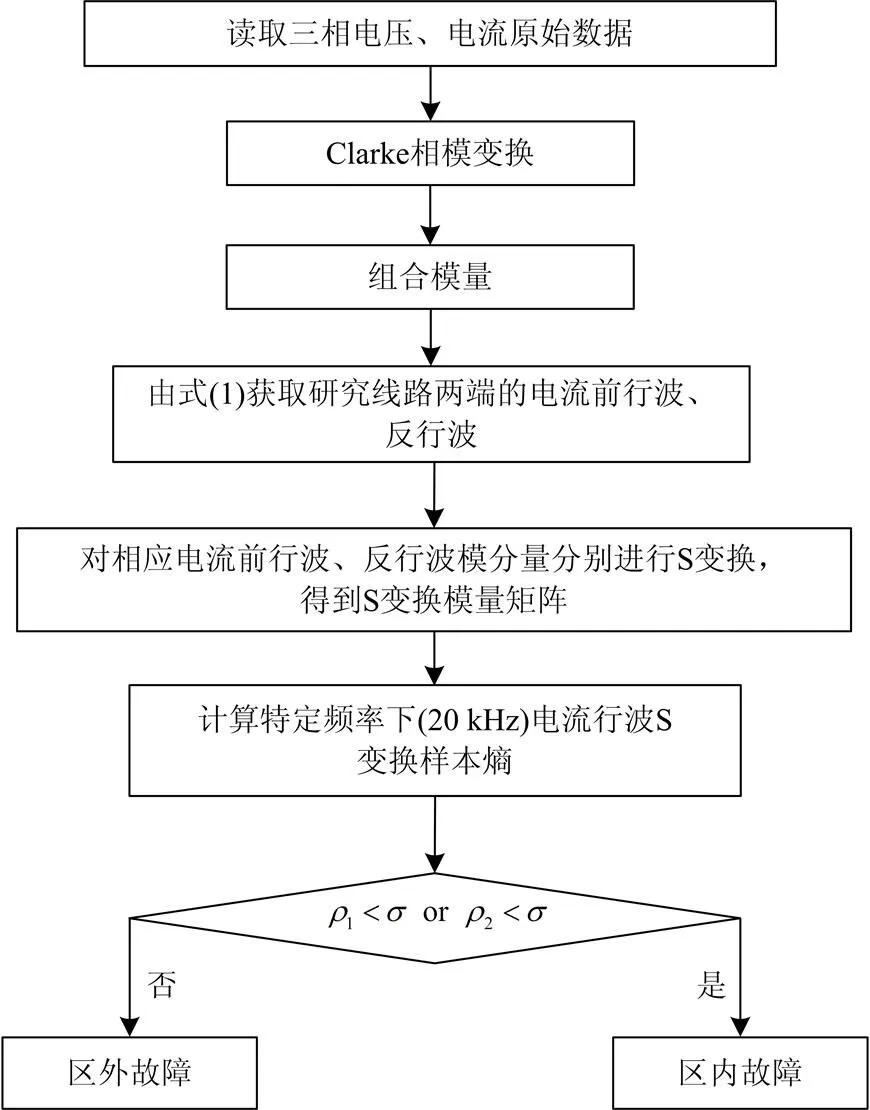
图 2 基于S变换样本熵的线路纵联保护算法流程

4 仿真分析

为验证上述线路纵联保护算法的正确性，采用PSCAD/EMTDC 建立图1所示三相输电系统仿真模型，线路均采用频率相关模型，其中1=2=150 km，3=200 km，4=120 km，母线杂散电容均设定为，采样频率设定为200 kHz，S变换后选择20 kHz对应的单频率电流方向行波作为计算对象，数据窗长度为故障后4 ms数据。

4.1 区内故障测试

设L3线路K2点(距C端50 km)发生ACG故障，接地电阻200 Ω，故障初始角45º，线路C端电流前行波和B端电流反行波波形如图3所示。依据本文算法，计算S变换初始模极大值对应时刻后3 ms内单频率故障电流方向行波样本熵，得到代入式(14)，可得,，满足判据(15)，判断故障发生在线路L3区内，保护动作。

4.2 区外故障测试

设线路L3区外K3点(距C端70 km)发生BCG故障，接地电阻200 Ω，故障初始角45°，线路C端电流前行波和B端电流反行波波形如图4所示。计算故障后4 ms内单频率电流方向行波样本熵，代入式(14)，可得，不满足式(15)，判断故障发生在线路L3区外，保护不动作。

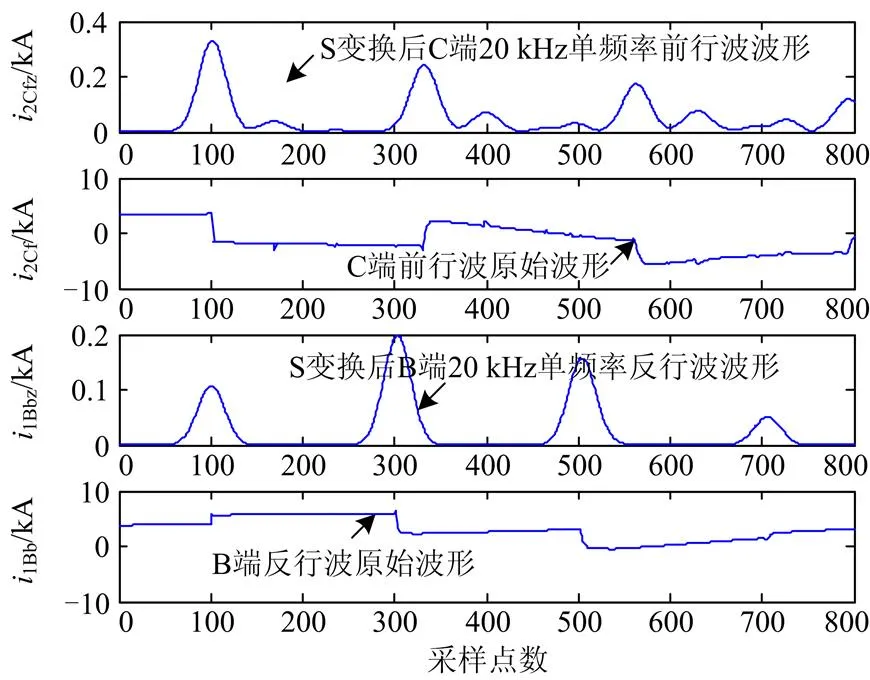
图3 区内故障时 L3线路两端电流行波波形

Fig. 3 Current waveform of L3internal fault

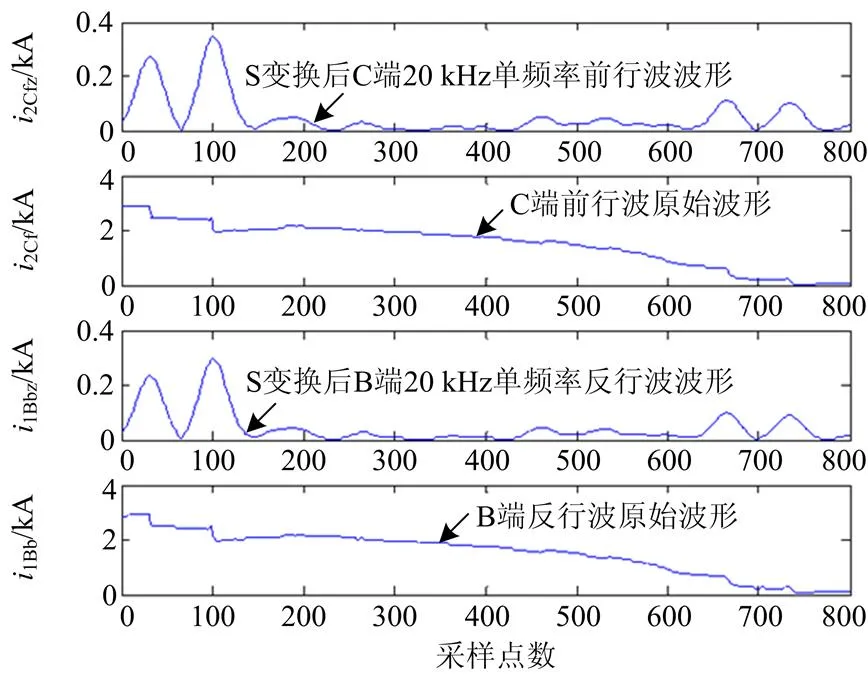
图4区外故障时 L3线路两端电流行波波形

4.3 相关因素讨论与分析

1) 故障接地电阻

为了验证不同故障接地电阻对保护算法的影响，论文进行了大量的仿真实验。设K2为线路L3区内故障点，K3为L3区外故障点，均设置为B相接地，初始角为 60º，不同接地电阻下保护的仿真判断结果如附录表A1所示。仿真结果表明，故障接地电阻的变化不会影响保护对区内外故障的正确识别。

2) 故障初始角

电压过零点附近故障时行波较微弱，提取困难。为验证算法在小故障初始角下的灵敏性，论文进行了相应的仿真分析。

分别设置区内故障点K2(距离母线B为80 km)和区外故障点K3(距离母线C为90 km)发生C相接地故障，接地电阻分别为50 Ω和200 Ω，仿真测试结果见附录表A2所示。由仿真结果可知，保护能正确判断不同故障初始角下的区内外故障，即使是小初始角故障情况下的区内外故障，保护仍能正确识别。

3) 不同故障类型

为验证算法在不同故障位置和故障类型下的保护动作性能，在线路L3的不同位置设定不同类型的故障(接地电阻100 Ω，故障初始角60º)，结果如附录表A3所示。由仿真结果可知，保护不受故障位置和故障类型的影响，均能准确动作。

4) 不同母线类型

电网中母线结构类型主要有[13]：(1) 如图1中母线B，母线上除被保护线路外还有两条及以上出线。 (2) 如图1中母线C，母线上除被保护线路外只有一条出线。(3) 如图1中母线D，母线上除被保护线路外，有变压器且没有其他出线。

从上述 R1和R2的仿真结果可知，第1类和第2类母线结构不对保护算法产生影响，这里主要分析第 3 类母线结构对算法的影响情况。此时被保护线路为L4，设置保护单元R3和R4分别安装在L4线路的C侧和D侧，故障点设置为K2(距C母线80 km)和K3(距C母线20 km)，故障类型为C相接地，仿真结果如附录表A4 所示。

附录表A4仿真结果表明，区外故障时，线路两端电流行波样本熵比值不受各种母线结构类型的影响，均接近于1；在区内故障时，由于第3类母线存在近乎全反射现象，可能导致该类型母线侧的电流前行波和线路对侧电流反行波样本熵比值接近1，但是该类型母线侧的电流反行波和线路对侧电流前行波样本熵比值仍然很小，满足判据(15)。综合分析，在任何故障类型下，保护均能正确判断区内外故障，动作性能不受母线结构类型的影响。

4.4 门槛值选取讨论

选择合适的门槛值对保护十分重要，直接影响保护的灵敏度。本文利用线路两端电流行波S变换样本熵的比值构成保护判据，选择门槛值主要考虑线路两端的行波样本熵值相对大小关系。区内故障时，线路两端电流行波不是同一行波，波形差异很大，样本熵值差异明显，由大量仿真结果看，两侧电流前反行波的样本熵比值最小值几乎都在0.5以内。而区外故障时，一端电流前行波和另一端电流反行波本质为同一行波，波形高度相似，样本熵值几乎一样，比值接近于1。综合考虑区内外故障保护的灵敏度，门槛值应在0.7~0.9为宜。仿真中论文采用的门槛值为 0.8，从上述大量的仿真数据可知，该值能使区内外故障都有足够的灵敏度。

5  结论

本文基于故障电流前行波、反行波理论，求取故障后一段时间内的故障电流单频率前行波和反行波S变换样本熵，利用线路两端样本熵比值识别区内外故障；同时，方案对各种影响保护的因素进行了详尽分析。仿真分析结果表明，所提保护算法需要的数据窗短，不受接地电阻、故障初始角、母线结构等的影响，能够正确识别区内外各种故障，不需要线路两端数据严格同步，通信量小。

附录

图A1区外故障时L3线路两端故障行波

Fig. A1 Waveform of travelling wave for L3external fault

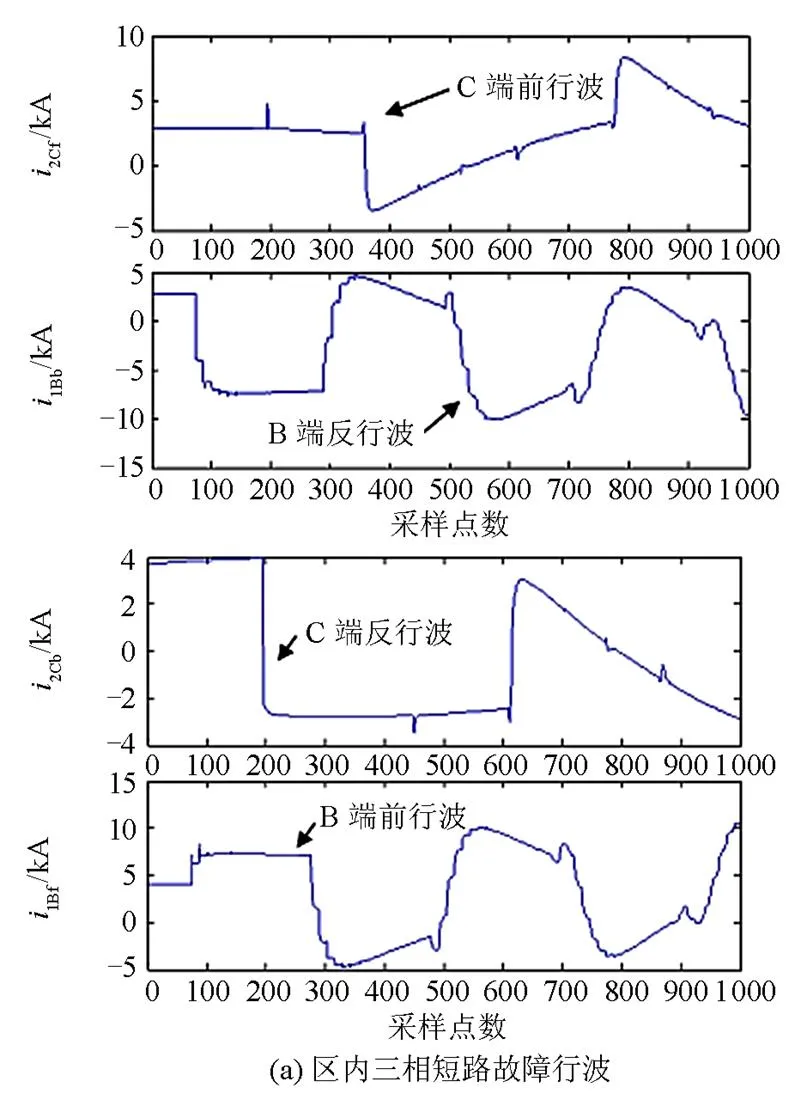
图A2区内故障时L3线路两端故障行波

Fig. A2 Waveform of travelling wave for L3internal fault

表A1不同接地电阻下保护算法的测试结果

Table A1 Test results of protection algorithm under different fault resistances

故障位置接地电阻/Ω判定结果 线路BC距B端50 km(K2)00.218 70.206 1区内 500.210 80.206 2区内 2000.213 60.240 1区内 5000.170 50.283 5区内 线路BC距C端50 km(K2)00.261 00.340 4区内 500.282 20.337 4区内 2000.26220.288 3区内 5000.285 20.278 9区内 线路BC距B端100 km(K2)00.263 20.103 3区内 500.2850.099 6区内 2000.290 90.102 8区内 5000.2450.116 6区内 线路CD距C端70 km(K3)00.992 40.992 1区外 500.957 20.988 7区外 2000.989 80.995 3区外 5000.981 30.998 5区外

表A2不同故障初始角下保护算法的测试结果

Table A2 Test results of protection algorithm under different fault inception angles

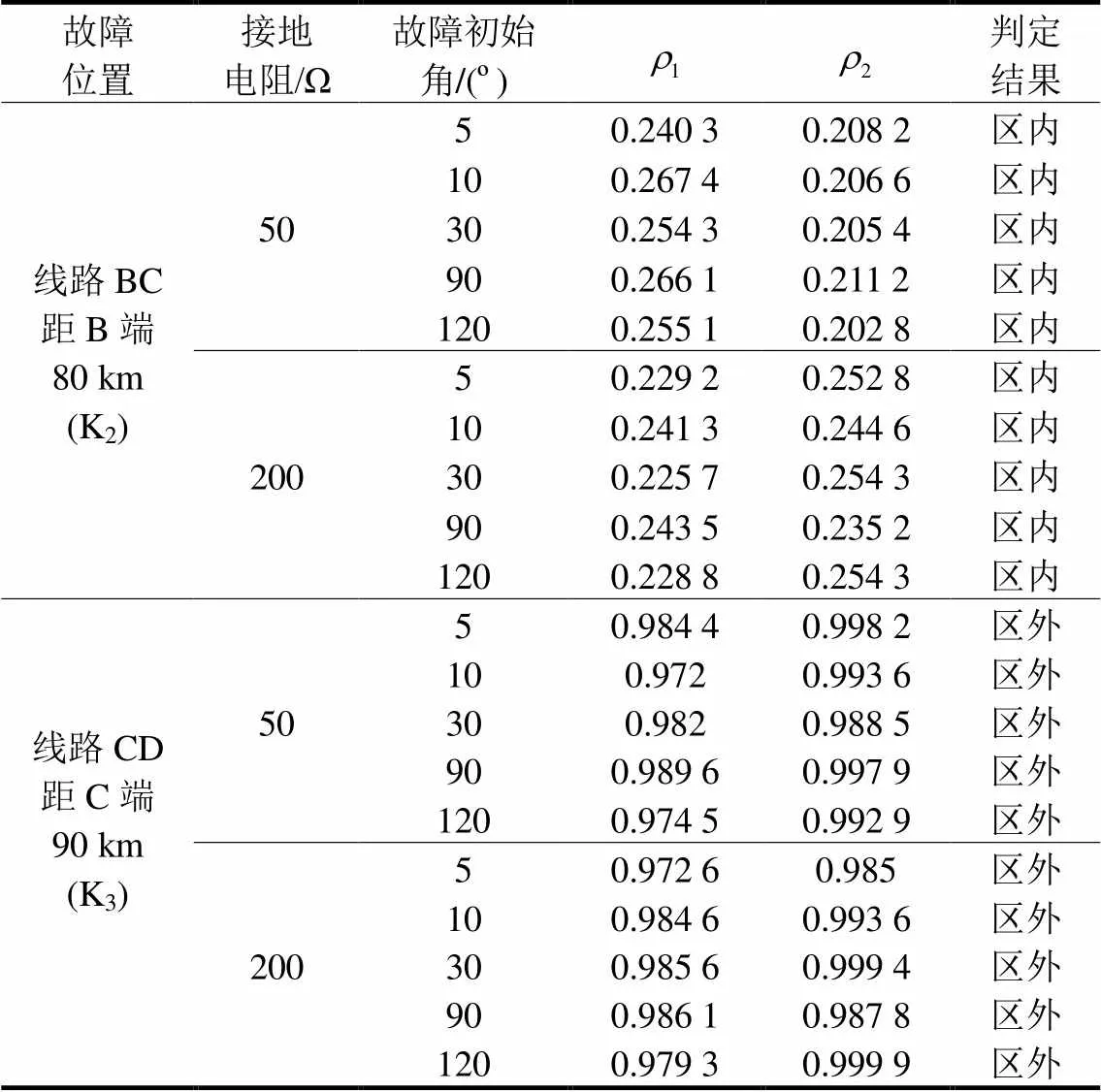
故障位置接地电阻/Ω故障初始角/(º)判定结果 线路BC距B端80 km(K2)5050.240 30.208 2区内 100.267 40.206 6区内 300.254 30.205 4区内 900.266 10.211 2区内 1200.255 10.202 8区内 20050.229 20.252 8区内 100.241 30.244 6区内 300.225 70.254 3区内 900.243 50.235 2区内 1200.228 80.254 3区内 线路CD距C端90 km(K3)5050.984 40.998 2区外 100.9720.993 6区外 300.9820.988 5区外 900.989 60.997 9区外 1200.974 50.992 9区外 20050.972 60.985区外 100.984 60.993 6区外 300.985 60.999 4区外 900.986 10.987 8区外 1200.979 30.999 9区外

表 A3不同故障位置和故障类型下保护算法测试结果

Table A3 Test results of protection algorithm under different fault positions and fault types

故障位置故障类型判定结果 线路BC距B端10 kmABC0.107 10.344 3区内 ABG0.112 20.399 8区内 CG0.100 40.318 5区内 BC0.107 40.347 7区内 线路BC距C端10 kmABC0.192 60.380 3区内 ABG0.216 80.479 5区内 CG0.210 50.252 2区内 BC0.192 70.385 3区内 线路BC距B端100 kmABC0.497 10.053 2区内 ABG0.322 0.074 7区内 CG0.259 40.102 1区内 BC0.495 20.053 8区内 线路L2(K1)距B端20 kmABC0.993 60.987 2区外 ABG0.976 60.997 1区外 CG0.997 80.985 4区外 BC0.999 40.975 3区外

表A4 不同母线结构下保护算法测试结果

Table A4 Test results of protection algorithm under different busbar configurations

故障位置接地电阻/W故障初始角/(º)判定结果 K22050.975 80.979 4区外 500.980 90.962 1区外 30050.9840.989 7区外 500.992 50.983 8区外 　K32050.948 60.156 5区内 500.952 20.156 5区内 30050.947 80.142 7区内 500.917 40.143 5区内

[1] 张苏敏, 古斌, 曹良丰, 等. 输电线路相差保护新原理[J]. 电力系统保护与控制, 2015, 43(2): 77-83.

ZHANG Sumin, GU Bin, CAO Liangfeng, et al. A novel phase comparison protection principle for transmission lines[J]. Power System Protection and Control, 2015, 43(2): 77-83.

[2] 曾铁军, 郑茂然, 苏泽光, 等. 基于突变量阻抗原理的差动保护的研究[J]. 电力系统保护与控制, 2014, 42(1): 115-118.

ZENG Tiejun, ZHENG Maoran, SU Zeguang, et al. Study on the differential protection based on the principle of variable impedance[J]. Power System Protection and Control, 2014, 42(1): 115-118.

[3] 马静, 裴迅, 马伟, 等. 基于故障分量虚拟阻抗的线路差动保护原理[J]. 电力自动化设备, 2014, 34(12): 58-69.

MA Jing, PEI Xun, MA Wei, et al. Differential protection principle based on virtual impedance of fault component for power transmission line[J]. Electric Power Automation Equipment, 2014, 34(12): 58-69.

[4] 韩昆仑, 蔡泽祥, 贺智, 等. 高压直流输电线路故障行波传播特性及其对行波保护的影响[J]. 电力系统保护与控制, 2013, 41(21): 20-25.

HAN Kunlun, CAI Zexiang, HE Zhi, et al. Propagation characteristic of fault traveling wave on HVDC line and its influence on HVDC line traveling wave protection[J]. Power System Protection and Control, 2013, 41(21): 20-25.

[5] 袁兆强, 张承学. 超(特)高压输电线路高速行波差动保护[J]. 电力自动化设备, 2012, 32(3): 13-17.

YUAN Zhaoqiang, ZHANG Chengxue. High speed traveling wave differential protection for EHV/UHV transmission line[J]. Electric Power Automation Equipment, 2012, 32(3): 13-17.

[6] 王全, 徐习东. 基于行波差动原理的线路保护实用判据[J]. 电力系统自动化, 2012, 36(1): 86-89.

WANG Quan, XU Xidong. Applied criterion for line protection based on traveling-wave differential principle[J]. Automation of Electric Power Systems, 2012, 36(1): 86-89.

[7] 邹贵彬, 高厚磊, 江世方, 等. 新型暂态行波幅值比较式超高速方向保护[J]. 中国电机工程学报, 2009, 29(7): 84-90.

ZOU Guibin, GAO Houlei, JIANG Shifang, et al. Novel transient travelling wave based amplitude comparison ultra high speed directional protection[J]. Proceedings of the CSEE, 2009, 29(7): 84-90.

[8] 孔飞, 张保会, 王艳婷. 基于行波波形相关性分析的直流输电线路纵联保护方案[J]. 电力系统自动化, 2014, 38(20): 108-113.

KONG Fei, ZHANG Baohui, WANG Yanting. A novel pilot protection scheme foe HVDC transmission lines based on waveform correlation analysis of traveling wave[J]. Automation of Electric Power Systems, 2014, 38(20): 108-113.

[9] 刘兴茂, 林圣, 何正友, 等. 基于S变换的新型波阻抗方向继电器[J]. 中国电机工程学报, 2013, 33(22): 113-119.

LIU Xingmao, LIN Sheng, HE Zhengyou, et al. A novel surge impedance directional relay based on S transform[J]. Proceedings of the CSEE, 2013, 33(22): 113-119.

[10] 何正友, 蔡玉梅, 钱清泉. 小波熵理论及其在电力系统故障检测中的应用研究[J]. 中国电机工程学报, 2005, 25(5): 38-43.

HE Zhengyou, CAI Yumei, QIAN Qingquan. A study of wavelet entropy theory and its application in electric power system fault detection[J]. Proceedings of the CSEE, 2005, 25(5): 38-43.

[11] 罗国敏, 何正友, 林圣. 利用小波相对熵的差异识别输电线路暂态信号的探讨[J]. 电网技术, 2008, 32(15): 47-51.

LUO Guomin, HE Zhengyou, LIN Sheng. Discussion on using discrepancy among wavelet relative entropy values to recognize transient signals in power transmission line[J]. Power System Technology, 2008, 32(15): 47-51.

[12] 何正友, 符玲, 麦瑞坤, 等. 小波奇异熵及其在高压输电线路故障选相中的应用[J]. 中国电机工程学报, 2007, 27(1): 32-37.

HE Zhengyou, FU Ling, MAI Ruikun, et al. Study on wavelet singular entropy and its application to faulty phase selection in HV transmission lines[J]. Proceedings of the CSEE, 2007, 27(1): 32-37.

[13] 李小鹏, 何正友, 武骁. 基于S变换能量相对熵的高压输电线路极性比较式纵联保护[J]. 电网技术, 2014, 38(8): 2250-2256.

LI Xiaopeng, HE Zhengyou, WU Xiao. Polarity comparison pilot protection based on S-transform energy relative entropy for high voltage transmission lines[J]. Power System Technology, 2014, 38(8): 2250-2256.

[14] 孙波, 徐丙垠, 孙同景, 等. 基于暂态零模电流近似熵的小电流接地故障定位新方法[J]. 电力系统自动化, 2009, 33(20): 83-87.

SUN Bo, XU Bingyin, SUN Tongjing, et al. New fault locating method based on approximate entropy of transient zero-module current in non-solidly earthed network[J]. Automation of Electric Power Systems, 2009, 33(20): 83-87.

[15] 赵志宏, 杨绍普. 一种基于样本熵的轴承故障诊断方法[J]. 振动与冲击, 2012, 31(6): 136-140.

ZHAO Zhihong, YANG Shaopu. Sample entropy-based roller bearing fault diagnosis method[J]. Journal of Vibration and Shock, 2012, 31(6): 136-140.

[16] 来凌红, 吴虎胜, 吕建新, 等. 基于EMD和样本熵的滚动轴承故障SVM识别[J]. 煤矿机械, 2011, 32(1): 249-252.

LAI Linghong, WU Husheng, LÜ Jianxin, et al. SVM recognition method based on emd and sample entropy in rolling bearing fault diagnosis[J]. Coal Mine Machinery, 2011, 32(1): 249-252.

[17] 刘兴茂, 林圣, 何正友, 等. 基于S变换的行波相位比较式方向继电器[J]. 电网技术, 2014, 38(3): 744-749.

LIU Xingmao, LIN Sheng, HE Zhengyou, et al. S transform based travelling wave phase comparison directional relay[J]. Power System Technology, 2014, 38(3): 744-749.

[18] 唐求,滕召胜, 高云鹏, 等. 基于S变换的平方检测法测量电压闪变[J]. 中国电机工程学报, 2012, 32(7): 60-67.

TANG Qiu, TENG Zhaosheng, GAO Yunpeng, et al. Voltage flicker measurement using square demodulation method based on S transform[J]. Proceedings of the CSEE, 2012, 32(7): 60-67.

[19] 王宇, 赵庆生, 郭贺宏, 等. 离散正交S 变换在电能质量扰动检测中的应用[J]. 电力系统保护与控制, 2015, 43(17): 93-97.

WANG Yu, ZHAO Qingsheng, GUO Hehong, et al. Application of discrete orthonormal S-transform in detection of power quality disturbances[J]. Power System Protection and Control, 2015, 43(17): 93-97.

[20] 吴浩, 李群湛, 南晓强, 等. 基于行波信息的广域后备保护故障判别新原理[J]. 电力系统及其自动化学报, 2012, 24(6): 83-89.

WU Hao, LI Qunzhan, NAN Xiaoqiang, et al. New principle of fault identification for wide-area back-up protection based on traveling wave information[J]. Proceedings of the CSU-EPSA, 2012, 24(6): 83-89.

(编辑 葛艳娜)

A new pilot protection principle based on S-transform sample entropy

WU Hao1, 2

(1. School of Electrical Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. School of Automation and Electronic Information Engineering, Sichuan University of Science & Engineering, Zigong 643000, China)

A new method of pilot protection based on S-transform sample entropy of current traveling wave for transmission lines is proposed, the ratio of S-transform sample entropy of fault current traveling wave at both ends of transmission line within a period of time after the occurrence of the fault is used to identify the internal and external fault. For the external fault, the forward traveling wave on the side and the backward traveling wave on the other side of transmission line are the same traveling wave, and the waveform is similarity, sample entropies of the corresponding current traveling wave are approximately equal to each other, so the ratio is close to one. For the internal fault, the forward traveling wave on the side and the backward traveling wave on the other side of transmission line are different, and the waveform is weak similarity, sample entropies of the corresponding current traveling wave have great differences, and the ratio is less than that of the external fault. According to these characteristics, a fault can be identified as internal or external one. The simulation result shows that the internal and external fault can be distinguished rapidly by the method presented in this paper, and its performance is not affected by fault types, fault inception angle, grounding resistance, fault location, and bus configuration.

transmission lines; pilot protection; fault traveling wave; S-transform; sample entropy

10.7667/PSPC150972

2015-06-10；

2015-10-08

吴 浩(1980-)，男，博士研究生，副教授，主要从事电力系统保护与控制方面的研究。E-mail: wuhao801212@ 163.com

人工智能四川省重点实验室项目(2013RYY01，2012RYY06，2014RYY05，2015RYY01)；自贡市科技局项目(2012D08)