基于单端口网络内电阻极性的电压暂降追源方法

时 昀，倪 冰，宋思松，周玉明



基于单端口网络内电阻极性的电压暂降追源方法

时 昀，倪 冰，宋思松，周玉明

(盱眙县供电公司，江苏 淮安 211700)

电压暂降追源即确定电压暂降扰动源相对于监测装置的位置。以对电网故障的分析为切入点，应用端口网络理论，将任何复杂电网在电压暂降源监测装置安装处等效为2个“有源单端口网络”。视电网故障为“有源单端口网络”的外部扰动，测量并计算出“有源单端口网络”的内电阻，依据“有源单端口网络”的内部电阻的极性，对电压暂降源相对于电压暂降源监测装置的位置进行判断。内电阻为正，电压暂降源与参考方向相反，即上游。内电阻为负，电压暂降源与参考方向相同，即下游。给出了内部电阻的计算方法。所提出的电压暂降源定位方法具有坚实的理论基础。仿真结果表明，该方法对辐射式、非辐射式，以及中性点有效接地和非有效接地的混合电网的电压暂降源定位准确率达到100%，是一种非常实用的电压暂降源定位法。

电能质量；电压暂降；源定位；序分量；空间矢量

0 引言

电压暂降，是指供电电压均方根值在短时间内下降至额定电压幅值的10%~90%，典型持续时间为10 ms~1 min的一种现象[1]。在现有的电能质量投诉中，电压暂降问题最为严重，占投诉比80%[2]。频频出现的电压暂降问题会对工业生产，特别是一些自动化程度很高的设备产生严重影响，以至于经济利益上蒙受巨大损失[3-4]。电能是一种由供、用电双方共同保证质量的特殊产品。对电压暂降源定位进行研究的意义在于，当电压暂降产生时，对引起暂降的源头进行追溯，可以为解决相应问题给予指导，并为界定供、用电双方责任给出依据。

暂降源定位，就是确定引起电压暂降的扰动源位于监测装置的哪一侧[5]。现有的暂降源定位法依其原理可归为两类。第一类，基于扰动功率流的方法。文献[6]最早提出了利用扰动能量和扰动功率初始峰值对电压暂降源进行定位的方法，文献[7]用小波分析对该方法进行了改进，文献[8-9]在该方法基础上引入扰动无功功率和无功能量，使之得到拓展。第二类，基于阻抗的方法。系统轨迹斜率法[5]与电流实部极性法[10-12]，较适用于对称故障的定位。文献[13]提出零序分量的判别法，对非对称扰动源定位准确度有所提高，但受算法限制定位准确率仍难满足要求。等效阻抗实部极性法[14]易受故障周期选择的影响。距离阻抗继电器法[15-16]适用于非辐射网络。文献[17]提出基于Hilbert变换的复阻抗判定法仅限于三相对称故障的判定。在此之外，文献[18]提出综合的判断方法为暂降源定位提供了新的思路。文献[19-21]表明现有暂降源定位方法能准确定位对称故障引起的电压暂降事件，对非对称故障引起的暂降定位准确率不高，而且不适用于非辐射式电网。因此对暂降源进行定位的方法需要进一步的研究。

1 确定电压暂降位置的思路

1.1 电压暂降源位置的定义

电压暂降源定位就是确定电压暂降源在监测装置的哪一侧[5]。为确定电压暂降源相对监测装置的位置，要选定一个“参考方向”。上文中介绍了现有电压暂降源定位方法都“规定”电网正常运行时基波有功电流的实际流动方向为参考方向。在该参考方向选定后，从监测装置安装处观察，电压暂降扰动源位置与参考方向的相同时，暂降源位于“下游”；反之则认定为“上游”。对于单电源辐射式配电网(如图1)，或是用户侧有自发电的双侧电源辐射式电网(如图1中用户侧电源E2仅供用电户自给用电，不会向供电侧反送电)，有功电流方向由电源指向负荷，参考方向是易于选定，且方向不变的。在这种确定参考方向的条件下，扰动在监测装置的上游即扰动位于监测装置的供电侧；反之，则位于监测装置的用户侧。但对于环网(如图2)或是双侧电源电网，实际有功电流方向与负荷大小、分布与电源的出力有关。即实际情况是随时间变化，各个监测点的参考方向不是“确定”的。因此，即使已做出了上下游的定位判断，仍不能确定暂降源相对监测装置的位置。所以，由此看来，现有的电压暂降源定位方法都不适用于包括环网在内的混合电网。为使该问题得到解决，本文提出的电压暂降源定位法使用监测装置的电流和电压互感器的极性(同名端)“确定”有功电流参考方向。正常情况下我们“规定”负荷消耗有功功率为有功电流的正参考方向，与监测点的实际有功电流的流向无关，如图2中下方的“→”。在参考方向明确的条件下，暂降源的相对位置很容易确定，将监测点合理分布，即可准确定位电压暂降源。因此，本文所提方法能适用于包括环网在内的混合电网。

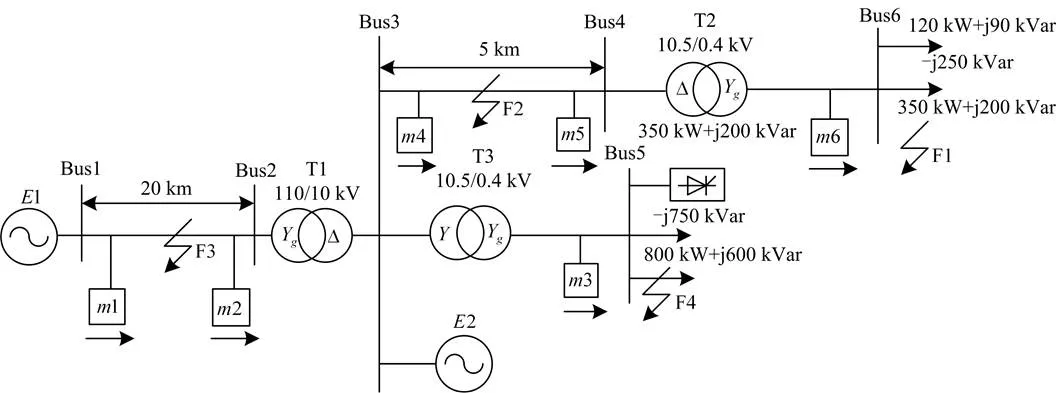
图1 单回路放射式电网

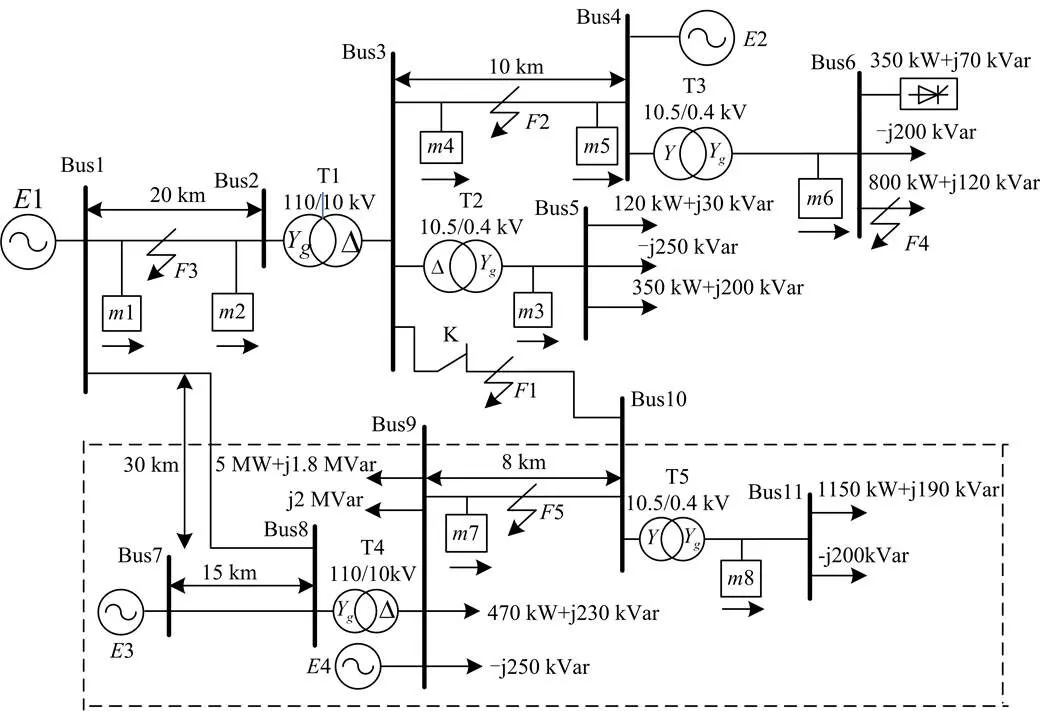
图2 手拉手供电网络

1.2 确定电压暂降位置的思路

电力系统中，电压暂降的起因是电网中存在扰动(如：短路故障、大电机启动、电容的投切等)。 以电力系统中典型的短路故障来说，在电力系统中几乎不可能同时出现两个及以上的短路故障。因此，我们在分析时认为电力系统中只存在一个短路故障的情况，并将电力系统中的元件认定为线性的。依据线性电路端口网络理论，对任何电网从电压暂降源(短路点)向两侧电能质量监测装置1和2观察，不管电网的拓扑结构多么复杂，对外部电路而言，都可以分别在监测装置1和2处等效为2个有源单端口网络。因配电网短路容量不是很大，可近似认为端口网络中的电源为理想电源。因此，对于外部电路，不管有源端口网络的内部有多复杂，总可以用一个理想电压源和一个线性阻抗相串联的有源支路来代替，如图3。图3中：为供电侧等效电源矢量，则定义为系统供电侧等效的内阻抗，，分别为用电侧等效电源矢量和内阻抗，和分别为扰动源到2个监测点的线路阻抗，1和2是2个监测点，下方“→”表示监测点有功电流的参考方向，为短路故障(即电压暂降扰动源)点。在点监测到的电压和电流矢量为

依据有源单端口网络的特性，若电流由有源单端口网络向外部电路流出，即发出有功功率，等值阻抗的实部为负，阻抗特性如图4中第一象限；若电流由外部流入有源单端口网络，即消耗有功功率，等值阻抗的实部为正，阻抗特性如图4中第二象限。按照本文对有功电流参考方向的“规定”：电阻消耗有功功率为有功电流的正参考方向。因此，在监测点监测到的计算值等于从电压暂降扰动源点向监测点观察，点等效端口网络的内部电阻值，符号决定于点的参考方向，当参考方向是从端口网络向外时，符号为“负”，如图3左侧1点端口网络，故障扰动源在与监测点有功电流参考方向的相同方向，即下游；相反，参考方向是从外部指向端口网络内部时，符号为“正”，如图3右侧2点端口网络，故障扰动源在与监测点有功电流参考方向的相反方向，即上游。即：

根据有源端口网络理论，任何网架结构都可以视为为图3所示等效网络模型，模型参数仅与电压暂降源扰动点在网架结构中的位置、电压暂降源监测装置的安装位置、网架结构和电网中各个元件的参数有关。因此，该方法适用于任何网架结构电网(辐射式、环式、单回路、单电源、多电源)的暂降源定位判断。

2 阻抗实部的计算方法

有源单端口网络等效电路内阻抗的实部可由式(4)计算得到

图3中点测得的有源单端口网络等效电路内电阻值如图6曲线。

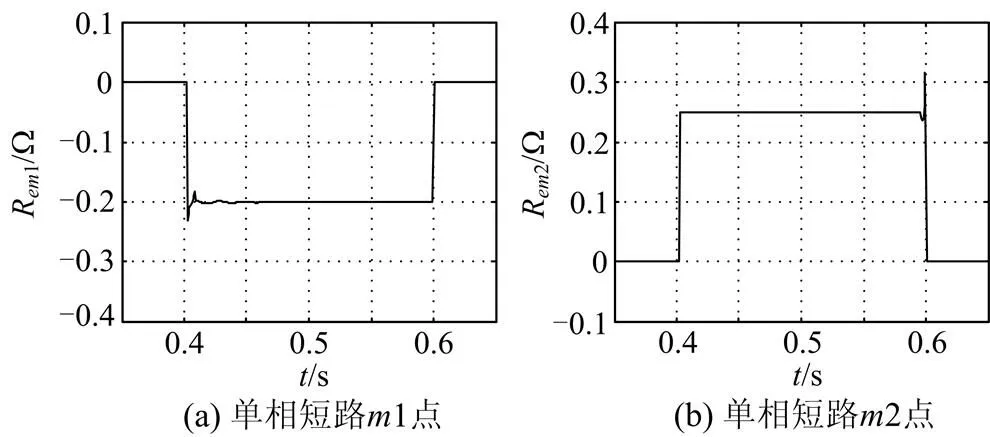
图6 三相短路故障mi测得的内电阻Remi

即不对称电压暂降负序扰动电压和电流矢量就是电压暂降期间的负序电压和电流矢量。这里，上标“-”表示“负序”。显然，按式(8)计算负序扰动电压和电流要比按式(6)计算正序扰动电压和电流更为简单。按照对称分量理论，式(9)和式(10)可提取得到监测点的电压和电流信号的负序对称分量如式(9)、式(10)所示。

对监测点的电压和电流信号每基波周期采样点，并且取为3的整数倍，由得到负序电压、电流采样值的离散表达式如式(11)、式(12)所示。

由式(8)可计算得负序有源单端口网络的等值内电阻为

图4中点的等值阻抗监测值如图7中曲线所示。

图7 不对称故障时测得的内电阻值Remi

虽然以上结论是假设图3是线性电路推得的，但“有源端口网络”等值阻抗的计算值与负荷无关，只要准确测量出监测点基波电压、电流的扰动矢量，就能准确计算出等值阻抗，因此，本文所提方法也同样适用于电路中有非线性负载(元件)的情况。综上所述，电压暂降源定位可遵循图8框图步骤。

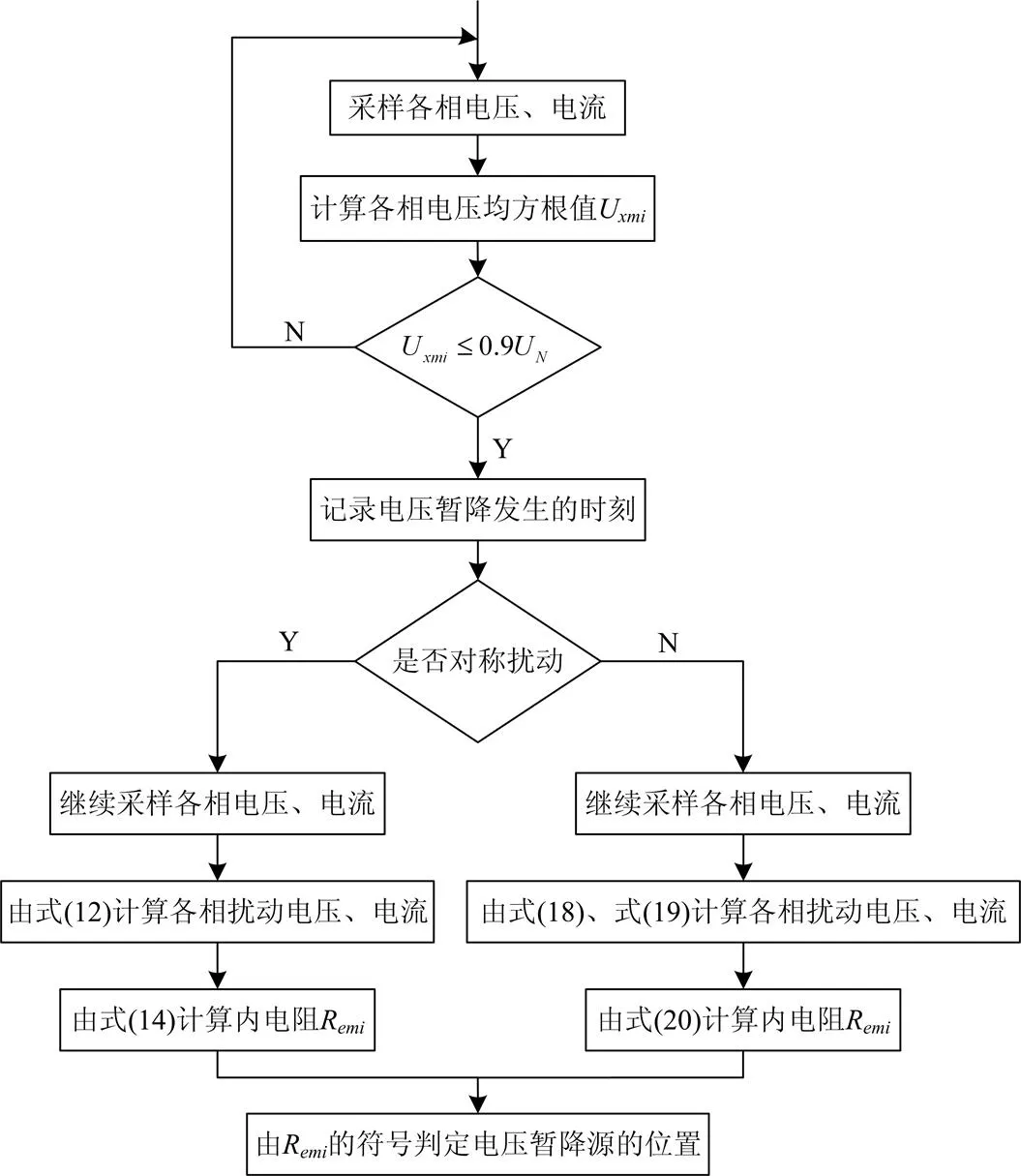
图8 所提方法的执行框图

Fig. 8 Flowchart of the proposed method

3 仿真验证

3.1 辐射式电网

用本文所提方法(SIR)对图1辐射式电网进行仿真，仿真判断结果见表1，定位准确率为100%。

表1 SIR暂降源定位方法的仿真判断结果

图1中E1是无限大电源，短路容量1 000 MVA，E2的容量为100 kVA ，实际发出有功功率33 kW。3个变压器的容量选取为6.3 MVA、1 MVA和1.25 MVA，其连接方式如图1所示。在所接负荷中，T3的负载侧连接一可控整流源作为非线性负荷。系统接地情况为：110 kV、380 V侧中性点接地，10 kV侧中性点不接地。仿真设置有4个故障点和6个监测点。F1、F2、F3和F4表示4个故障点，1、2、3、4、5和6表示6个监测点。每个故障点都以4种故障类型进行仿真，依次为单相接地短路、两相接地短路、两相短路和三相短路。相应的故障类型在表1的“()”内表示，如F1(1)、F2(1,1)、F3(2)和F4(4)分别表示F1单相接地、F2两相接地短路、F3两相短路和F4点三相短路。该仿真实验给定的参考方向如图1监测装置下方“→”所示。表1中“↓”表示下游，“↑”表示上游，“*”表示观测点三相电压均未达到电压暂降标准，不作暂降源定位判断。

3.2 非辐射式电网

本文所选手拉手供电网如图2所示，仿真参数如下：E1、E3为无穷大电源，短路容量分别为1 000 MVA、1 200 MVA。E2、E4选型分别为QR-60-2、QR-30-2，实际出力为52 kW、25 kW，'d依次为21、21.7。变压器容量分别为6.3 MW、1 MW、1.25 MW、6.3 MW、1.25 MW，其连接方式及所接负荷见图2。用本文所提方法对图2所示手拉手供电网进行仿真，8个观测点参考方向如图2中“→”所示，仿真判断结果见表2，定位准确率为100%。证明本文所提方法适用于任何网架结构。

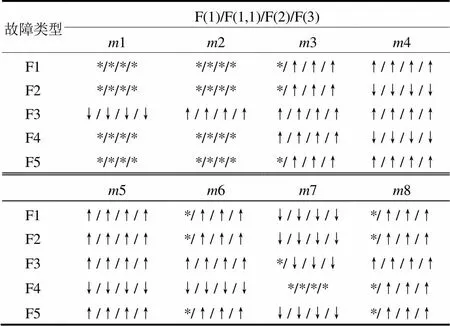
表2 SIR暂降源定位方法的仿真判断结果

3.3 大电机启动

大电机启动的仿真模型，由图1所示放射电网中T2变压器的350+j200 kVA负荷替换为等容量的异步电机构成。图9(a)为异步电机在0.4 s启动时观测点3测量到的电压、电流波形。图9(b)为异步电机启动时3和4测量点得到的端口网络内部电阻值。，该扰动源位于3下游；，扰动源位于4上游，与实际情况相符。其余观测点电压降低未达到电压暂降源定义范围(小于90%额定相电压)，不作定位判断。

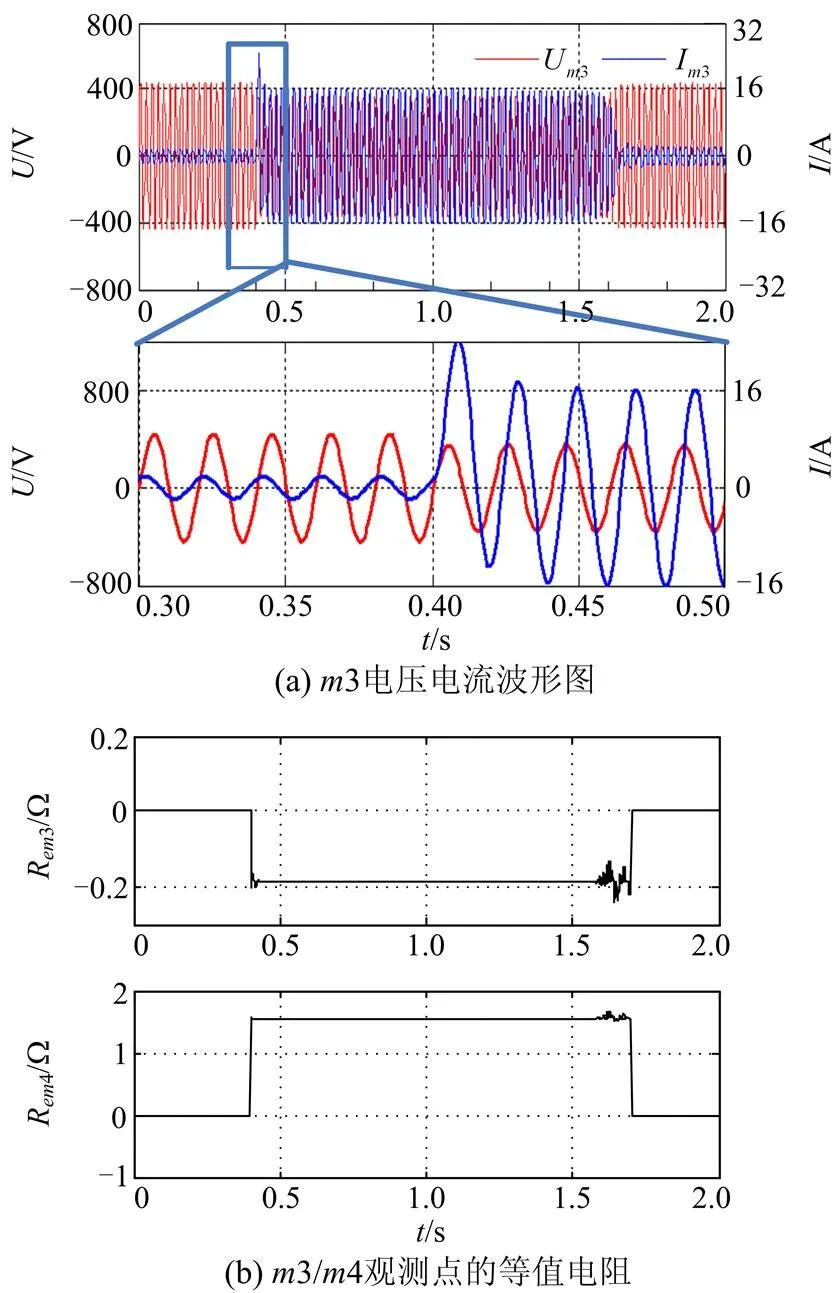
图9感应电机启动

4 结论

从电压暂降源点向电网两侧观察，任何电网都可以在电压暂降源监测装置安装处分别等效为2个有源单端口网络，并都可以用有源单端口网络等效代替。按照有源单端口网络内电阻的符号，可准确地定位暂降源的方向。内电阻的符号为正时，扰动在监测点参考方向的相反方向，即上游；内电阻的符号为负时，扰动在监测点参考方向的相同方向，即下游。所提电压暂降源定位方法依据线性电路端口网络理论，有坚实的理论基础，因此，可确定性地定位暂降源。由于本文所提定位方法仅通过基波电压和电流计算、判断，与电路中的负载性质(线性与非线性)无关，因此，适用于有非线性负荷电网的电压暂降源定位。所提方法是基于有源端口网络理论，从扰动源点向监测点观察，任何复杂网架结构的电网在电压暂降源监测装置的安装位置都可以等效为一个有源单端口网络，因此，该方法适用于任何网架结构电网(辐射式、环式、单回路、单电源、多电源)的暂降源定位判断。虽然本文所提方法是按照电网故障扰动推导分析而得的结论，但该方法同样适用于其他扰动(如：电容投切、变压器投切、大电机启动等)的暂降源定位。

[1] IEEE Std. 1159-1995 recommended practice for monitoring electric power quality[S]. Draft 5. 1995.

[2] GRANAGHAM M F, MUELLER D R, SAMOTYJ M J. Voltage sags in industrial systems[J]. IEEE Transactions on Industry Applications,1993, 29(2): 397-403.

[3] 陶顺, 肖湘宁, 刘晓娟. 电压暂降对配电系统可靠性影响及其评估指标的研究[J]. 中国电机工程学报, 2005, 25(21): 63-69.

TAO Shun, XIAO Xiangning, LIU Xiaojuan. Study on distribution reliability considering voltage sags and acceptable indices[J]. Proceedings of the CSEE, 2005, 25(21): 63-69.

[4] SAMOTYJ M J, MIELEZARSKI W, WASILUK-HASSA M M. Electric power for the digital age[C] // 10th international Conference on Harmonics and Quality of Power, Brazil, 2002, l: 276-282.

[5] LI C, TAYJASANANT T, XU W, et al. Method for voltage-sag detection by investigating slope of the system trajectory[J]. IEE Proc Gen, Transm, and Distrib, 2003, 150(3): 367-372.

[6] PARSONS A C, GRADY W M, POWERS E J, et al. A direction finder for power quality disturbances based upon disturbance power and energy[J]. IEEE Transactions on Power Delivery, 2000, 15(3): 1081-1086.

[7] 杨杰, 王金浩, 章雪萌, 等. 基于小波多分辨率分析的电压暂降源定位研究[J]. 电力系统保护与控制, 2010, 38(22): 90-95.

YANG Jie, WANG Jinhao, ZHANG Xuemeng, et al. Analysis of voltage sag source location based on wavelet multiresolution method[J]. Power System Protection and Control, 2010, 38(22): 90-95.

[8] LEBORGNE R C, MAKALIKI R. Voltage sag source location at grid interconnections: a case study in the zambian system[C] // IEEE Lausanne PowerTech. 2007: 1852-1857.

[9] KONG Wei, DONG Xinzhou, CHEN Zhe. Voltage sag source location based on instantaneous energy detection[C] // Electric Power System Research, 2008, 78: 1889-1898.

[10] HAMZAH N, MOHAMED A, HUSSAIN A. A new approach to locate the voltage sag source using real current component[J]. Electric Power System Research, 2004, 72(2): 113-123.

[11] HAMZAH N, MOHAMED A, HUSSAIN A. Locating voltage sag source at the point of common coupling in industrial distribution systems[C] // IEEE PEDS 2005: 532-537.

[12] GAO Jie, LI Qunzhan, WANG Jia. Method for voltage sag disturbance source location by the real current component[C] // Power and Energy Engineering Conference, 2011: 1-4.

[13] POLAJZER B, STUMBERGER G, SEME S, et a1. Detection of voltage sag sources based on instantaneous voltage and current vectors and orthogonal Clarke’s transformation[J]. IET Gener Transm Distrib, 2008, 2(2): 219-226.

[14] TAYJASANANT T, LI C, XU W. A resistance sign-based method for voltage sag source detection[J]. IEEE Transactions on Power Delivery, 2005, 20(4): 2544-2551.

[15] KUMAR A, ROUTRAY A. Applying distance relay for voltage sag source detection[J]. IEEE Transactions on Power Delivery, 2005, 20(1): 529-531.

[16] YU Yilin, XU Yonghai. Research of method for voltage sag source detection in power distribution network[C] // 6th IEEE Conference on Industrial Electronics and Applications, 2011: 485-488.

[17]程志友, 王雪菲, 徐佳. 一种基于复阻抗的电压暂降定位方法[J]. 电力系统保护与控制, 2016, 44(4): 149-154.

CHEN Zhiyou, WANG Xuefei, XU Jia. A voltage sag detection method based on complex impedance[J]. Electrical Measurement & Instrumentation, 2016, 44(4): 149-154.

[18]吕干云, 吴育聪. 电压暂降源定位的优化综合判据法[J]. 电力系统保护与控制, 2013, 41(5): 66-71.

LÜ Ganyun, WU Yücong. Optimization comprehensive criterion of voltage sag source location[J]. Power System Protection and Control, 2013, 41(5): 66-71.

[19] 何维国, 董瑞安, 张孝银, 等. 配电网中电压暂降源定位方法比较[J]. 电测与仪表, 2011, 48(8): 53-58.

HE Weiguo, DONG Ruian, ZHANG Xiaoyin, et al. Comparison of methods for voltage sag source detection in distribution system[J]. Electrical Measurement & Instrumentation, 2011, 48(8): 53-58.

[20]赵莹, 赵川, 叶华, 等. 应用主成分分析约简电压暂降扰动源识别特征的方法[J]. 电力系统保护与控制, 2015, 43(13): 105-110.

ZHAO Ying, ZHAO Chuan, YE Hua, et al. Method to reduce identification feature of different voltage sag disturbance source based on principal component analysis[J]. Power System Protection and Control, 2015, 43(13): 105-110.

[21] 张逸, 林焱, 吴丹岳. 电能质量监测系统研究现状及发展趋势[J]. 电力系统保护与控制, 2015, 43(2): 138-147.

ZHANG Yi, LIN Yan, WU Danyue. Current status and development trend of power quality monitoring system[J]. Power System Protection and Control, 2015, 43(2): 138-147.

(编辑 周金梅)

Voltage sag source location method based on the polarity of single port network internal resistance

SHI Yun, NI Bing, SONG Sisong, ZHOU Yuming

(Xuyi Power Supply Company, Huaian 211700, China)

Locating the voltage sag source is to determine on which side of a monitoring device the voltage sag originates. This paper takes the analysis of power grid faults as an entry point and applies the port network theory, and then any complex power network at both sides of voltage sag source monitoring devices can be equivalent into two active single-port networks respectively. Grid faults are regarded as external disturbances of “active single-port network”, meanwhile the internal resistance of the “active single-port network” will be measured and calculated. Based on the sign of internal resistance in these two active single-port networks, the voltage sag source location relative to the monitoring devices can be identified accurately. If the sign of internal resistance is positive, the location of voltage sag source is opposite to the reference direction, that’s upstream. If the sign of internal resistance is negative, the location of voltage sag source is consistent with the reference direction, that’s downstream. Calculation method of internal resistance is given. The proposed method has a solid theoretical basis. Simulation results show that this method can locate voltage sag source with an accuracy of 100% in power networks with various topologies, such as radial or non-radial power systems as well as the network adopted neutral grounded effectively or ineffectively. It is a practical and effective method for voltage sag source location.

power quality; voltage sag; source location; sequence component; space vector

10.7667/PSPC152112

2015-12-05；

2016-06-25

时 昀(1974-)，女，高级工程师,长期从事电力生产技术及管理工作。