张峰水库大坝渗透参数反演计算

贾慧鹏

（山西张峰水库建设管理局，山西晋城 048215）



张峰水库大坝渗透参数反演计算

贾慧鹏

（山西张峰水库建设管理局，山西晋城 048215）

【摘 要】本文以坝体竣工时试验和检测得出的土性参数为初始值，以安全监测得出的现状渗流场为标准，通过有限元数值分析方法反演得出符合工程实际的坝体和坝基渗流计算参数。该参数用于预测高水位下坝体渗流变化情况，分析坝体在高水位下的渗透安全和渗流变化规律。

【关键词】张峰水库大坝；渗透参数；反演计算

1　工程概况

张峰水库坝型为黏土斜心墙堆石坝，坝顶高程763. 8m，坝顶长627m，坝顶宽10m，最大坝高72. 2m，上游坝坡1∶1. 75，下游坝坡1∶1. 50；黏土防渗体顶部高程762. 8m，顶宽4m，高程752. 5m以上采用直心墙型式，以下为斜心墙，心墙上游边坡1∶0. 75，下游边坡1∶0. 25；上游堆石料与心墙之间设置一层反滤层和一层过渡层，心墙下游与堆石料之间设置两层反滤层和一层过渡层。

2　计算模型

坝基岩分为强风化层、弱风化层和完整基岩，其中完整基岩又分为强透水层和中透水层两种。坝体土体按照其填筑类型分为心墙、2A和2B反滤层、3A过渡层、3B过渡层、4A和4B坝壳料五种。

计算时，将帷幕灌浆层和固结灌浆层统一考虑，并考虑了心墙下混凝土垫板和灌浆廊道；将基岩中透水率小于1Lu的下限作为计算模型下边界，以此作为不透水边界，并保证模型上下高度大于2倍坝高，模型左右两侧边界各取到坝趾与坝踵以外1倍坝高以外，这样确定的坝体模型长为500m，高为154m。

计算中库区和上游坝坡上实际上游水头边界，上游水头按照计算类别分别取实际库水位或者正常蓄水位等，下游水位按照原型观测结果基本在698～700m之间变化，实际取值时在计算上游较低水位时取699m，库水位较高时取700m。

为了计算方便，将底部高程620m作为计算模型的起始高程，也就是实际坝体620m高程为计算模型的0m高程，这样模型计算得到的水头高程与实际高程的换算关系为：

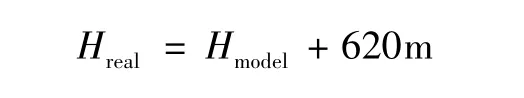
在坝体下游坝坡底部设定溢出边界条件，迭代计算坝坡溢出点的位置。

计算中以坝体高程方向为y轴，其0点为620m高程；以从上游指向下游为x轴，其0点为坝体模型上游边界点。得到的二维计算模型示例如图1所示。

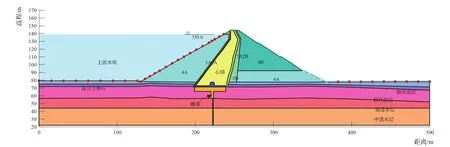
图1　二维计算模型示例（0＋350断面）

3　渗透参数反演计算

反演分析以0＋350断面为主进行。该断面处于坝体河床段，坝高最大，下游排水情况明确，并包含了几乎所有的填筑土料层，较为适合进行分析计算。

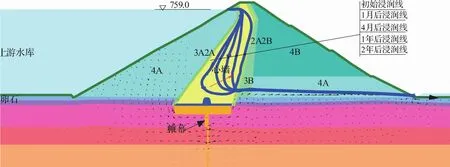
图2　库水位为759m时坝体浸润线变化过程

3. 1稳定与非稳定渗流场对比

用非稳定渗流计算方法，对坝体库水位瞬间抬升到正常蓄水位759m，之后持续1个月后、4个月后和1年后、2年后的浸润线进行了计算，用来对比非稳定渗流场向稳定渗流场转化的过程。计算结果如图2所示。从图2中看出，坝体浸润线在初期表现为心墙上游侧和底面702m高程以下浸湿，浸湿范围较小，浸润线为一个凹面向上的勺形；随着库水位在759m上维持时间增加，心墙内浸湿范围逐步增大，上游侧浸湿范围逐步向下游扩大，底部浸湿范围逐步向上抬升，1年后，形成了几乎垂直的浸润线；2年后，浸润线进一步移动和抬升，形成了稳定渗流浸润面，该面为一个凹面向下的勺形，这时心墙下部基本处于浸湿饱和状态，只有上部处于非饱和状态。

从上面的分析看出，坝体浸润锋面变化的过程实际上主要是心墙内部浸润线变化的过程，其他部位变化较小，也反映出心墙在整个坝体防渗中的重要地位。坝体心墙浸润线变化是从上游侧向下游侧和从底部向上抬升的变化过程，开始时的浸润线为下凹形，最后逐渐变化为上凸形。这些规律可以为下一步反演分析提供基础依据。

3. 2渗透参数反演分析

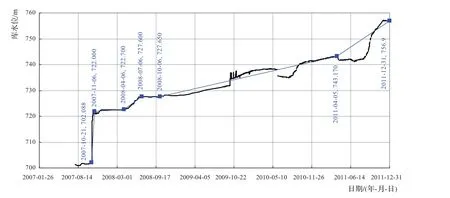
图3　蓄水过程线

以0＋350断面为例进行分析原型观测数据发现，实际库水位变化过程是一个逐渐上升的过程，在这一过程中，测定的坝体浸润线实际上是坝体在不同水位下非稳定渗流形成的过程，应采用非稳定渗流计算方法才能准确反映实际情况，因此反演的方法为非稳定渗流计算方法。

将模型上游水位边界条件按照实际库水位上升过程线（见图3）设置成为水位随时间变化的量，下游水位从698m到700m逐步抬升，计算坝体在不同时刻的浸润线变化，并将其与原型监测测定的不同时刻的坝体浸润线进行对比，若计算结果不同，根据实际情况调整计算参数，再进行计算，反复多次，直到计算坝体浸润线与原型观测浸润线基本一致为止，这时使用的计算参数就是符合实际的参数值，也就是反演得到的渗流计算参数值。通过这个过程就实现了参数的反演。

多次计算最后得到的坝体不同时刻的计算结果见图4。

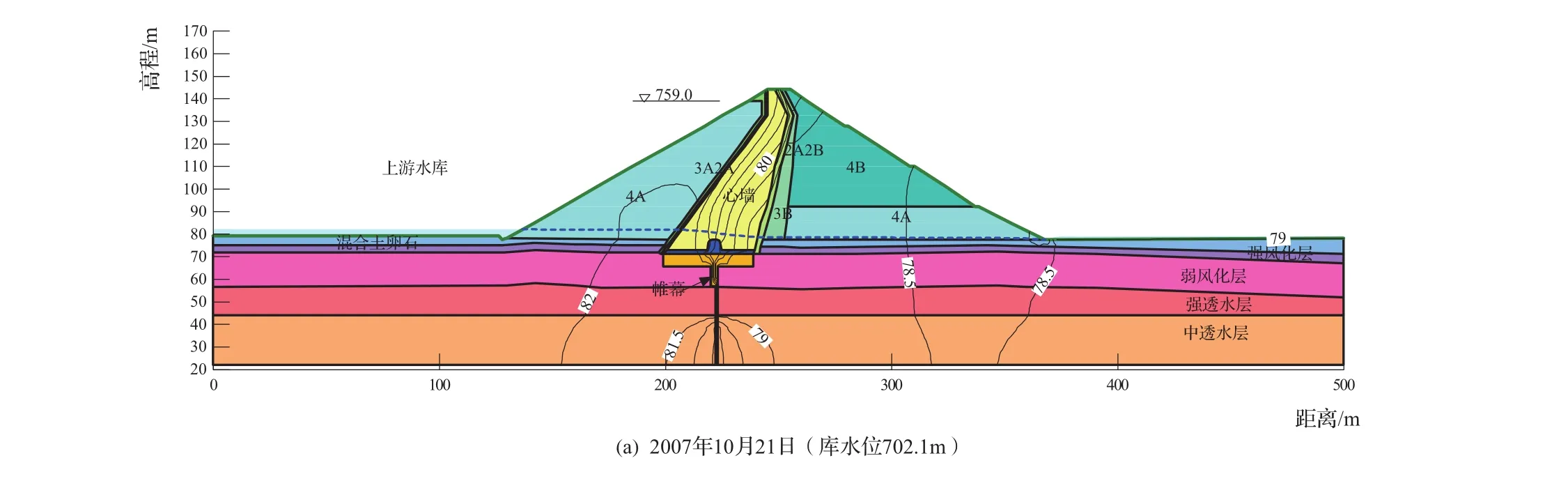
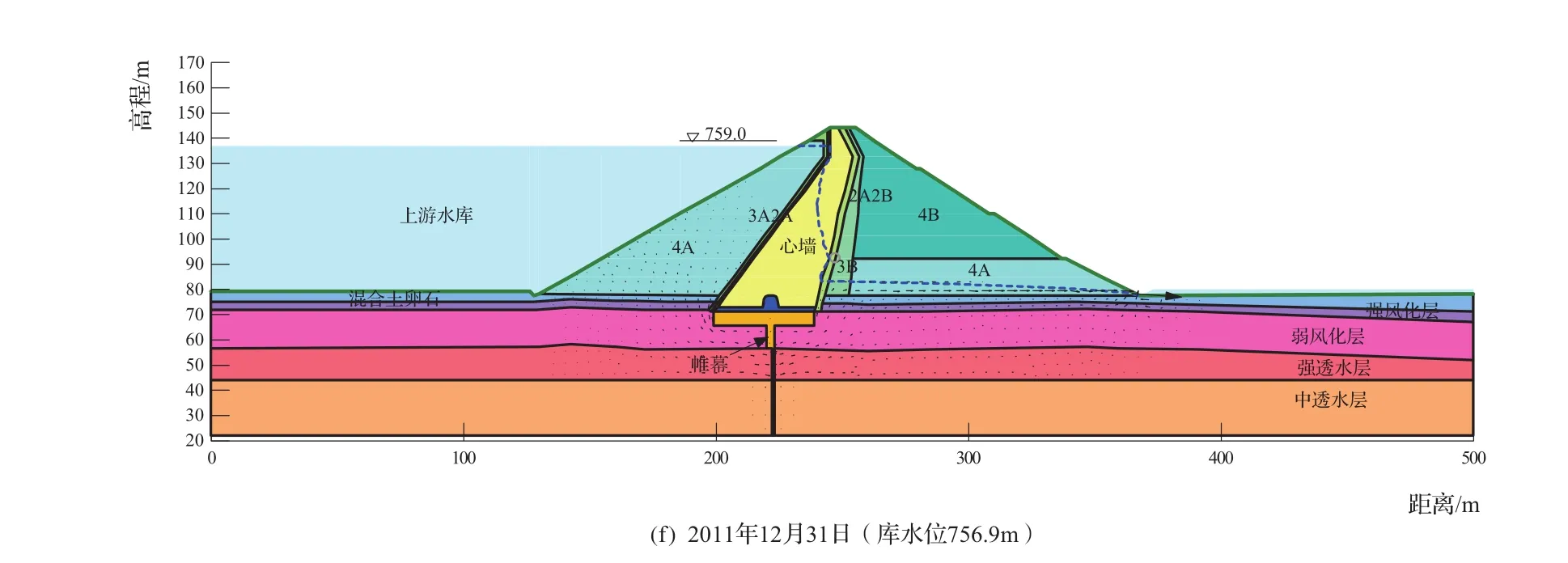
图4　0＋350断面不同时刻坝体浸润线

将图4与渗压计资料分析报告推测的坝体各个时刻浸润线进行对比发现，两者基本规律一致，数值相差不大。另外将计算得出的测点p-3-3-3点的渗透水头变化过程与计算得出的值进行对比，如图5所示，从图5中看出两者基本规律一致，数值有所差别，最大差值在3m左右，差别是在时间上有所滞后。另外反复计算表明：无论如何改变计算参数，在坝体下游，4A和3B区域底部浸润线都不会高于704m，而实际观测出该处渗透水头可以达到713. 59m（2011年12月31日，P-3-4-7）和709. 88m（2010年3月4日，P-3-3-6），可能因为该处为非饱和渗流补给区，局部渗透水压造成测点水压的变化，也可能与这两个测点精度不好有关。总体看来反演计算结果与实测值的发展规律与趋势一致，因此反演结果基本可以反映实际坝体渗流变化过程。

图5　0＋350断面测点p-3-3-3计算与观测水头变化对比情况

因此认为反演结果可信，由此得出的坝体渗透计算参数见右表。其中，坝体渗透系数与初始值一致，坝基岩体计算渗透系数有所增大，其他变化较小，坝体渗透系数与吸力的关系曲线基本相同。用以上反演得到的渗透计算参数就可以分析坝体渗透场，判别其渗透稳定性。

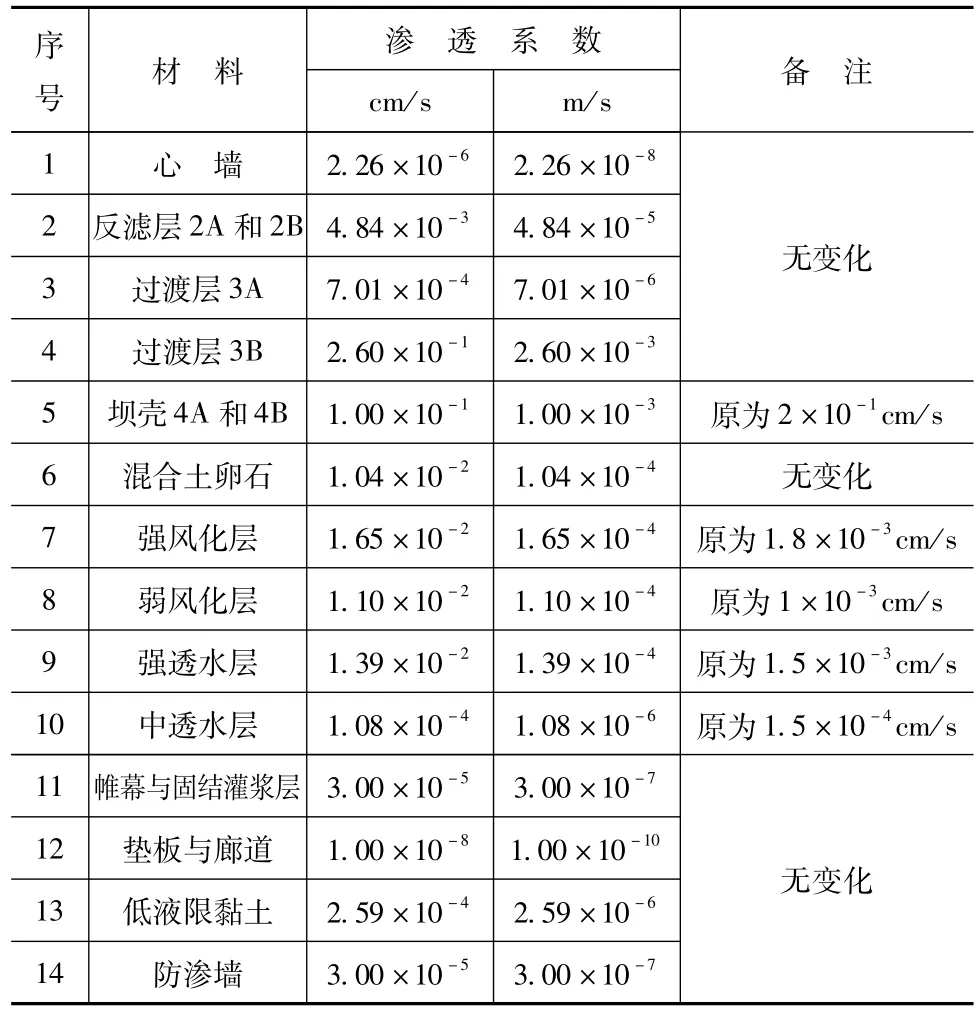
反演得到的各区域渗透系数对比表

4　结 语

以库水位在较高情况下实际观测得到的渗流场为标准进行参数反演，得出符合工程实际的坝体和坝基渗流计算参数；再以低库水位下渗流场观测结果为标准，用反演得到的计算参数进行渗流数值计算，验证反演参数的合理性；为下一步分析预测在正常高水位下坝体的渗流场及其渗透稳定性变化规律等奠定了坚实基础。■

Inversion calculation of dam seePage Parameter in Zhangfeng Reservoir

JIA Huipeng
（Shanxi Zhangfeng Reservoir Vonstruction Administration，Jincheng 048215，Vhina）

Abstract：Soil property parameters obtained from test and inspection during dam body completion are adopted as initial value. Current seepage field obtained from safety monitoring is adopted as standard. The dam body and dam foundation seepage calculation parameter in line with project practice are obtained through the inversion of finite element numerical analysis method. The parameter is used for predicting dam body seepage change position under the high water level. Seepage safety and seepage change rule of dam body under the high water level are analyzed.

Key Words：Zhangfeng Reservoir dam；seepage parameter；inversion calculation

DOI：10.16617／j.cnki.11-5543／TK.2016.01.018

中图分类号：TV139. 1

文献标识码：B

文章编号：1673-8241（2016）02-0062-05