一类自参数动力吸振器减震系统的Hopf分岔分析

秦　爽, 张建刚, 俞建宁, 杜文举

(1.兰州交通大学数理学院, 甘肃　兰州　730070; 2.兰州交通大学交通运输学院, 甘肃　兰州　730070)



一类自参数动力吸振器减震系统的Hopf分岔分析

秦爽1, 张建刚1, 俞建宁1, 杜文举2

(1.兰州交通大学数理学院, 甘肃兰州730070; 2.兰州交通大学交通运输学院, 甘肃兰州730070)

[摘要]通过系统运动的拉格朗日方程和牛顿第二定律,建立了振动系统的运动方程，并对一类带有粘性阻尼摆的自参数动力吸振器减振系统的复杂动力学行为进行研究.通过非线性动力学理论,分析该系统平衡点的稳定性，选择适当的分岔参数证明了Hopf分岔的存在.最后,通过数值仿真证明理论分析的正确性.

[关键词]自参数吸振器系统;稳定性;Hopf分岔;Lyapunov系数;周期轨道

动力吸振通过动力吸振器吸收主系统振动的能量,达到使主系统振动降低的目的.目前,已有许多以摆或者类似于摆的作用为辅助系统的自参数振动系统的研究.Hatwal等对两自由度自参数振动系统在受到谐波外激励作用时产生的周期和混沌运动进行研究,辅助系统采用的是单摆上附加的扭转弹簧[1-3].Cuvalci等分析研究了一个以单摆为辅助系统的悬臂梁自参数振动系统[4].Banerjee等采用高阶平均法对两自由度自参数弱非线性振动系统的分岔及其通往混沌的道路进行研究与探讨[5].

Hopf分叉在实际问题中有着广泛的应用，它是一类比较简单但又必不可少的动态分叉问题.由于它密切联系着自激振动产生的问题，所以在动态分叉研究和极限环研究中有着重要的理论价值和研究意义.目前学者们已经发表了很多有关分叉的文献和专著[6-9].

JerzyWarminski等讨论了一个附加阻尼摆的自参数吸振器系统的主参共振区的不稳定性[8].文献[9]在此基础上采用多尺度法讨论了该系统的平衡解,并通过罗斯-霍尔维兹判据判断其稳定性条件.但是,文献[8,9]并没有对系统的Hopf分岔行为进行研究.本文详细研究该系统的Hopf分岔行为，通过对系统的第一Lyapunov系数的计算，分析了该系统的Hopf分岔的方向，最后为验证理论推导的正确性，对该系统进行数值仿真.

1模型的建立

考虑一个带有粘性阻尼摆的自参数动力吸振器减振系统的动力系统,其结构示意图如图1所示.该系统主要由质量为m1的物块和非线性弹簧组成的非线性振子以及质量分别为mp、m2的杆和小球组成的单摆这两个子系统构成,并且此单摆附着在质量为m1的物块的一个支点处.记此处单摆的粘性阻尼系数为cφ.因为系统受到外激励作用,我们将这个非线性振子受迫于一个线性的弹簧.

假定此系统的弹簧振子是非线性Duffing型振子,即有F=kx+k1x3.将自参数动力吸振器系统运动的广义坐标定为垂直方向位移x和其上附着单摆的角度位移φ,运用拉格朗日方程和牛顿第二定律,可以得到此模型所对应的微分方程：

(1)

其中，单摆的长度记为l,单摆与质块m1的粘性阻尼系数记为cφ，非线性振子中阻尼的阻尼系数记为c.

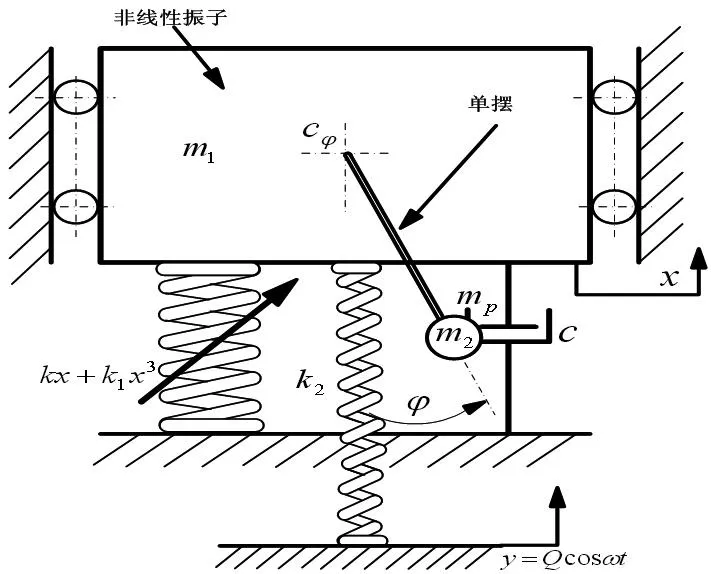
图1　自参数动力吸振器系统力学模型

为了方便研究与分析,选取新的时间尺度和长度尺度,将自参数动力吸振器系统进行无量纲化,令

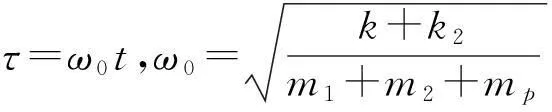
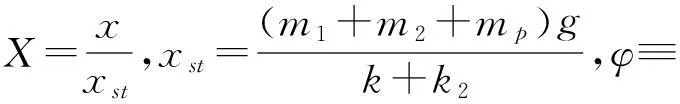
对方程(1)进行无量纲化：

(2)

其中对应的无量纲系数分别为：

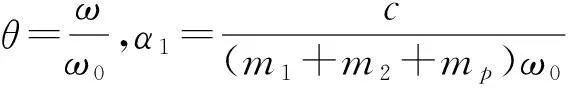
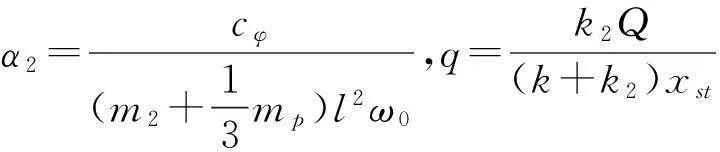
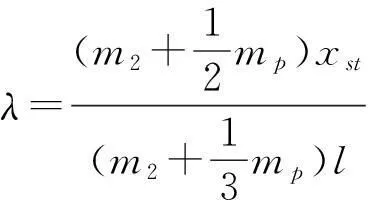
这里,单摆角度位移φ的二阶导数(摆动加速度)和φ的一阶导数(摆动速度)的平方这两个耦合项引起了方程(2)的自参数激励.对无量纲化运动微分方程(2)进行转化,转化为一阶微分方程组的形式,即

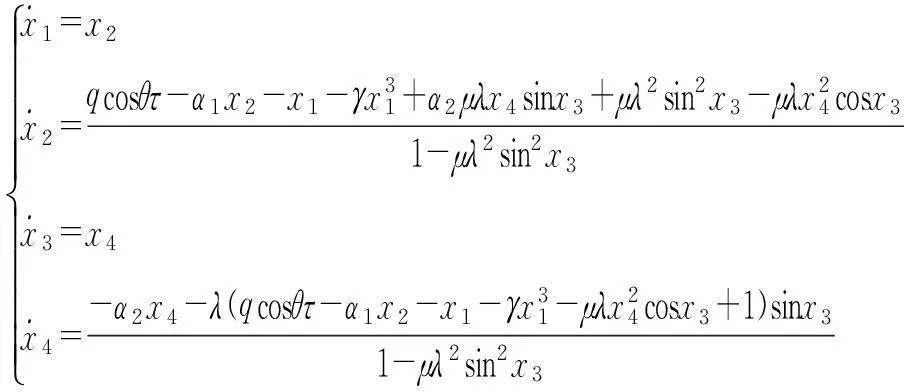
(3)

固定α1=0.26,α2=0.1,q=2.45,μ=17.228,λ=0.127,γ=0,θ=0.6时,系统(3)可以得到如图2(a)~(d)所示的一个混沌吸引子.

把系统(3)化为五维的自治系统,采用Wolf算法,计算得到系统(3)的5个Lyapunov指数分别为:λ1=0.061 1,λ2=0,λ3=-0.102 9,λ4=-0.170 1,λ5=-0.211 1.利用Kaplan-Yorke猜想公式,求出Lyapunov维数DKY=2.593 78.图3(a)~(d)为系统(3)的时间响应图、庞加莱截面、Lyapunov指数谱图及功率谱图.

2平衡点稳定性分析

令x5=cosθτ,x6=-θsinθτ,将系统(3)化为六维自治系统

(4)

图2　系统(1)在不同空间的吸引子

图3　(a) 时间响应图　(b) x1-x2平面的庞加莱截面　(c) Lyapunov指数谱图　(d)功率谱图

显然,E0=(0,0,0,0,0,0)恒为系统(4)的平衡点.为了简便,本文只讨论平衡点E0处的稳定性以及Hopf分岔情况.

系统(4)在平衡点E0处的Jacobian矩阵为

(5)

求得系统(4)在平衡点E0处Jacobian矩阵的特征方程为

p(ξ)=k0ξ6+k1ξ5+k2ξ4+k3ξ3+k4ξ2+k5ξ+k6

(6)

其中，k0=1,k1=α1+α2,k2=θ2+α1α2+λ+1,k3=α1θ2+α2θ2+α2+λα1,k4=θ2+α1α2θ2+λθ2+λ,k5=α2θ2+α1λθ2,k6=λθ2.

根据Routh-Hurwitz判据,知方程(6)的所有特征值都具有负实部,当且仅当

k1>0,Δi>0(i=2,3,4,5),k6>0.

(7)

定理1选λ为分岔参数,λ=λ0使得

ki>0(i=0,1,…,6),Δi>0(i=1,2,3,4)

(8)

成立时,系统(4)发生Hopf分岔,其中λ0为Hopf分岔的临界值.

3平衡点E0处的Hopf分岔分析

先回顾文献[11]中介绍的对于四维系统Hopf分岔的第一Lyapunov系数的求法, 然后进行理论分析.考虑以下系统

x′=f(x,ζ)

(9)

其中x∈R6,ζ∈Rm分别是系统的状态变量和控制参数.假设系统(9)有一个平衡点x=x0,ζ=ζ0,并且变量x-x0仍然记为x,则F(x)=f(x,ζ0)的泰勒展开式为

(10)

其中A=fx(0,ζ0),并且对i=1,…，6有

(11)

假设在平衡点(x0,ζ0)处系统(9)有一对纯虚根λ1,2=±iω0,(ω0>0),而且系统其他特征值具有非零实部.

令p,q∈C6，满足

Aq=iω0q,ATp=-iω0p,〈p,q〉=1

(12)

其中AT为A的转置，则第一Lyapunov系数可以定义为

(13)

其中，

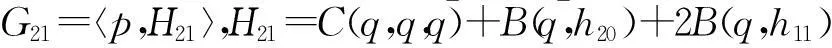
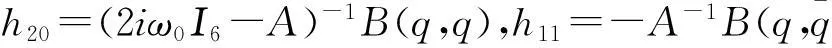
I6为6×6的单位矩阵.

取参数α1=0.26,α2=0.1,q=2.45,μ=17.228,γ=0,θ=0.6时可以求得Hopf分岔临界值λ0=0.135 14,并且有

k0=1,k1=0.36,k2=1.521 1,k3=0.264 7,

k4=0.553 1,k5=0.048 6,k6=0.048 6,

Δ1=0.36,Δ2=0.282 9,Δ3=0.020 7,

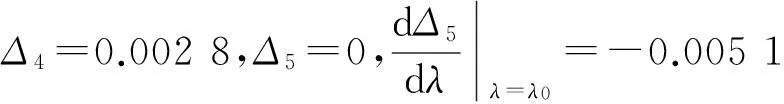
显然,定理1条件满足.当参数λ变化经过λ0=0.135 14时,系统(4)在平衡点E0处发生Hopf分岔.

下面通过求解系统(4)的第一Lyapunov系数,判断Hopf分岔的稳定性.在给定的参数下,系统(4)在平衡点E0处Jacobian矩阵的特征方程为

p(ξ)=ξ6+0.36ξ5+1.5211ξ4+0.2647ξ3+

0.5531ξ2+0.0486ξ+0.0486

(14)

方程(14)的6个特征值分别为

λ1,2=±0.6002i,λ3,4=-0.13±0.9915i,

λ5,6=-0.0499±0.639i.

根据(11)式,可以得到对应于f的线性函数

B(x,y)=(0,0.6293(x3y3-x4y4)+

0.2328(x3y4+x4y3),0,0.1352(x1y3+x3y1)+

0.0351(x2y3+x3y2)-0.3311(x3y5+x5y3),0,0)T,

C(x,y,z)=(0,1.5418(x5y3z3+x3y5z3+x3y3z5)-0.1636x3y2z3-0.6293x3y1z3,0,0.6293×

(x3y4z4+x4y4z3+x4y3z4)-0.0629(x4y3z3+x3y4z3+x3y3z4)-0.4139x3y3z3,0,0)T

(15)

通过直接计算可以求得满足(12)式的特征向量

q=(-1.004-3.2201i,-0.6026-1.9329i,

-0.3992-0.6889i,-0.2396-0.4135i,

-1.6673i,1)T,

p=(0.6767+1.06i,1.4788-1.4677i,

-5.3643-6.1859i,-11.4875+7.0152i,

-0.7633+0.6083i,-1.0139-1.2722i)T.

并且有

B(q,q)=(0,-47.887+104.15i,0,-1.0471+

0.4303i,0,0)T,

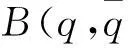
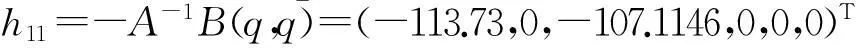
h20=(-39.27+208.86i,-250.63-47.12i,

13.35-18.8i,22.57+16.02i,0,0)T,

B(q,h11)=(0,313.36-128.5i,0,-4.1365+

86.0414i,0,0)T,

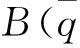
12.7225i,0,0)T,

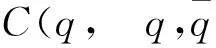
-41.3933-80.845i,0,0)T,

H21=(0,625.7397+1.8826i,0,-47.8663+

78.5153i,0,0)T,

G21=956.36-2199.5i.

定理2系统(4)在平衡点E0处的第一Lyapunov系数为

(16)

因此,系统(4)在平衡点E0处发生亚临界的Hopf分岔,并且产生一个不稳定的极限环.

4数值仿真

为验证理论分析的正确性,本文选取λ=0.14>λ0,λ=λ0=0.135 14,λ=0.12<λ0,分别得到系统(4)的3组时间响应图和相图,如图4~图6所示.当λ=0.12<λ0时,平衡点是稳定的;当λ=0.14>λ0时,平衡点是不稳定的.数值模拟与前一节的理论相符,系统(4)在平衡点E0处发生的Hopf分岔是亚临界的Hopf分岔,并且产生一个不稳定的极限环.

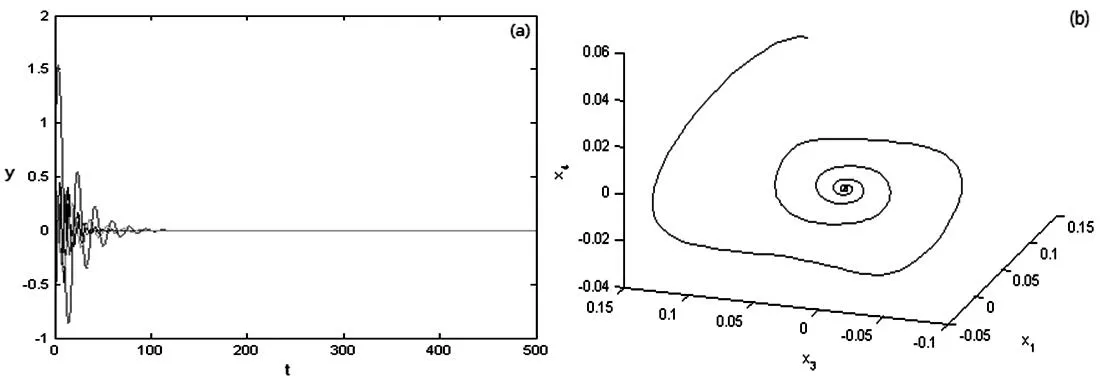
图4　当λ=0.12时系统(4)的时间响应图和相图

图5　当λ=λ0=0.135 14时系统(4)的时间响应图和相图

图6　当λ=0.14时系统(4)的时间响应图和相图

5结论

本文通过严格的数学推导及数值仿真研究了一类带有粘性阻尼摆的自参数动力吸振器减振系统,对该系统平衡点的稳定性理论进行分析,并且通过选取适当的分岔参数,证明了系统在分岔参数穿过临界值时发生Hopf分岔，并计算得到系统的第一Lyapunov系数，进而判定系统分岔的方向和稳定性；最后通过数值模拟验证了理论推导的正确性.

[参考文献]

[1]HATWALH,MALLIKA,GHOSHA.Non-linearvibrationsofaharmonicallyexcitedautoparametricsystem[J].JournalofSoundandVibration, 1982, 81(2):153-164.

[2]HATWALH,MALLIKA,GHOSHA.Forcednonlinearoscillationofanautoparamericsystem-partⅠ:periodicresponses[J].JournalofAppliedMechanics, 1983(50):657-662.

[3]XUJ,YUP.Delay-inducedbifurcationsinanonautonomoussystemwithdelayedvelocityfeedbacks[J].InternationalJournalofBifurcationandChaos, 2004, 14(8):2777-2798.

[4]CUVALCIO,ERTASA.Pendulumasvibrationabsorberforflexiblestructures:experimentsandtheory[J].JournalofVibrationsandAcoustics,1996,118:558-566.

[5]BANERJEEB,BAJAJAK,DAVIESP.Resonantdynamicsofanautoparametricsystem:astudyusinghigher-orderaveraging[J].InternationalJournalofNon-linearMechanics,1996(31):21-39.

[6]DIASFS,MELLOLF,ZHANGJG.NonlinearanalysisinaLorenz-likesystem[J].NonlinearAnalysis:RealWorldApplications, 2010(11):3491-3500.

[7]李险峰,张建刚,褚衍东,等.一个新类Lorenz混沌系统的动力学分析及电路仿真[J]. 动力学与控制学报,2007,5(4):324-329.

[8]WARMINSKIJ,KECIKK.Instabilitiesinthemainparametricresonanceareaofamechanicalsystemwithapendulum[J].JournalofSoundandVibration, 2009, 322(3):612-628.

[9]张文娟,俞建宁,杨留猛.自参数振动系统的稳定性分析[J].河北师范大学学报(自然科学版),2013,37(2):138-142.

[10]KUZNETSOVYA.Elementsofappliedbifurcationtheory[M].NewYork：AppliedMathematicalSciences, 2004.

(责任编辑吴强)

Hopf bifurcation analysis in an autoparametric dynamic vibration absorber

QIN Shuang1, ZHANG Jiangang1, YU Jianning1, DU Wenju2

(1. School of Mathematics and Physics, Lanzhou Gansu 730070, China;2. School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou Gansu 730070, China)

Abstract：The complex dynamic behavior of the autoparametric vibration absorbing system is studied. The dynamical equation of the system is established using Lagrangian and Newton’s second law. More precisely, the stability of the equilibrium points were studied by means of nonlinear dynamics theory. The existence of Hopf bifurcation is investigated by choosing the appropriate bifurcation parameter. Besides, numerical simulation is given to illustrate the theoretical analysis.

Key words：autoparametric vibration absorbing system; stability; Hopf bifurcation; Lyapunov coefficients; periodic orbits

[中图分类号]O322

[文献标志码]A

[文章编号]1673-8004(2016)02-0027-06

[作者简介]秦爽(1992—) ,女, 黑龙江大庆人, 硕士, 主要从事非线性系统动力学及其控制方面的研究.

[基金项目]国家自然科学基金项目(61364001).

[收稿日期]2015-11-25