基于Spark的Apriori算法的改进

牛海玲，鲁慧民，刘振杰

(长春工业大学计算机科学与工程学院，吉林 长春 130012)



基于Spark的Apriori算法的改进

牛海玲，鲁慧民，刘振杰

(长春工业大学计算机科学与工程学院，吉林 长春 130012)

[摘要]基于Spark大数据框架，将传统Apriori算法进行并行化处理，提出了一种改进的并行化AMRDD算法，使Apriori算法能够适用于大数据关联规则的挖掘.该算法利用Spark基于内存计算的抽象对象存储频繁项集，通过引入矩阵概念减少扫描事务数据库的次数，应用局部剪枝和全局剪枝方法缩减生成候选频繁项集的数量.通过搭建Spark平台实现该算法，并与传统Apriori算法和基于Hadoop的Apriori算法进行性能上的比较. 结果表明，该算法能够较大程度地提高大数据关联规则挖掘的效率.

[关键词]Apriori；Spark；矩阵；局部剪枝；全局剪枝

0引言

随着大数据时代的到来，云计算技术的兴起，如何从海量数据中高效地提取知识是目前急需解决的问题.同时，人们越来越关注数据挖掘技术在大数据环境下的应用，很多学者在该领域进行了改进研究，如数据分类、聚类方面等[1-2].关联规则挖掘作为数据挖掘的一个重要组成部分，在数据挖掘中扮演重要角色，作为关联规则中的经典算法Aprioi的地位更是举足轻重.然而传统的串行算法已经不能满足大数据时代的要求，因此新型的挖掘模式成为人们新的选择.

近年来，随着Hadoop和Spark等云计算平台的开源化，采用云计算并行编程框架，将传统的数据挖掘算法进行分布式并行化处理，提高大数据挖掘的效率，已成为数据挖掘领域的一个热点.本文将经典的Apriori关联规则挖掘算法基于Spark框架进行改进，提出了一种分布式并行化AMRDD算法，使之能够适用于大数据关联规则的挖掘.同时，算法采用矩阵向量结构减少扫描数据库的次数，应用局部剪枝和全局剪枝策略减少候选项集的数目，从而提高大数据环境下Apriori算法关联规则挖掘的效率.

针对Apriori算法需多次扫描数据库和可能产生大量频繁项集的缺点，人们提出了很多改进算法.包括基于概念格的频繁项集挖掘算法、基于频繁模式树的分布关联规则挖掘算法及在Apriori算法基础上进行改进的算法.[3-5]

文献[6]基于Hadoop平台提出一种MapReduceApriori，该算法针对Apriori的一些缺陷和Hadoop在大集群中表现出的优势，用HDFS来存储数据，以MapReduce方式实现并行处理，用于海量数据中发现频繁项集，处理效率明显比传统算法高，且表现出很好的加速比；文献[7]提出AprioriMMR算法，引入了矩阵的概念，通过矩阵与运算计算项目集的支持度，结合MapReduce计算框架，改进和优化了频繁项集的产生，在海量数据挖掘中大大提高了效率，不足之处是求解局部频繁项集的过程无剪枝操作，生成的候选项集数目过大；文献[8]基于MapReduce框架提出一种有效的关联规则算法ScadiBino，该算法首先将数据离散化处理转换为二进制，其次通过N个mappers和一个reducer过程，直接得到关联规则，而不是寻找频繁项集，有效地降低了执行时间.本文提出了一种改进的并行化AMRDD算法，使Apriori算法能够适用于大数据关联规则的挖掘.

1基于Spark的Apriori算法改进

Spark是一个通用的大规模数据快速处理引擎，主要提供基于内存计算的抽象对象RDD，允许用户将数据加载至内存后重复地使用.Spark编程模型参考MapReduce，不同的是Spark基于内存的计算特点在某些应用的实验性能上超过MapReduce 100多倍.Spark平台完全由Scala语言编写，Scala是一种融合了面向对象和函数式的编程语言，它专门为分布式而设计，精简且具有并发的威力.

RDD的基本操作[9]包括转换(Transformation)和动作(Action).可通过Scala集合或Hadoop数据集构造一个新的RDD，或通过已有的RDD产生新的RDD，例如map，filter，groupBy，reduceBy.Action是通过RDD计算得到一个或者一组值，例如count，collect和save.Spark中的所有转换都是惰性的，不会直接计算结果，只是记住应用到基础数据集(例如一个文件)上的这些转换动作.只有当发生一个要求返回结果给Driver的动作时，这些转换才会真正运行，这个设计让Spark更加有效地运行.

1.1基于Spark的Apriori算法基本思想

在Hadoop上实现基于矩阵的Apriori算法思想[7]，引入矩阵概念，只需2次扫描数据集D，结合Spark技术框架，并运用局部剪枝性质和全局剪枝性质改进频繁项集产生的过程，提高关联规则挖掘的效率.事务数据集及频繁项集的存储基于Hadoop的HDFS文件系统.矩阵的行为事务的集合，矩阵的列为项的集合，向量矩阵存储变量为0和1，可以减少数据存储空间，减少扫描次数，根据向量的操作规则，只需在矩阵中使用“与”操作即可快速产生项集的支持度.根据Spark内部运行机制，整个Spark编程框架均是基于对RDD的操作，算法命名为AMRDD.具体算法描述为：

(1) 扫描事务数据库，求频繁1项集的集合L1.

(2) 存储在HDFS上的事务数据库即为一个RDD，RDD被平分成n个数据块，并且这些数据块被分配到m个work节点进行处理.

(3) 构造局部矩阵.设Di为事务数据库中的某一个数据块(1≤i≤n)，假定L1的个数为H，Di中事务数目为J，则用L1和Di构造H×(J+2)矩阵Gi，其中第1列为L1中的项，最后一列为L1中对应项的支持度计数，Gi中的其余各列为Di中的事务T，若T中存在对应于L1中的项，则相应位置1，否则置0.矩阵向量的具体转换如图1所示.

TIDItemsT0I0,I3,I5T1I3,I4T2I0,I2,I3T3I0,I1,I2,I5T4I1,I4T5I0,I2,I3,I6T6I2,I3,I5T7I1,I2,I4T8I0,I2,I6划块→T0I0,I3,I5T1I3,I4T2I0,I2,I3T3I0,I1,I2,I5T4I1,I4T5I0,I2,I3,I6T6I2,I3,I5T7I1,I2,I4T8I0,I2,I6根据L1构建矩阵→I01012I10011I21113æèççöø÷÷G1I00011I11012I20011æèççöø÷÷G2I00011I11113I21000æèççöø÷÷G3

图1矩阵向量的转换

(4) 用Gi生成候选项集的局部支持度.含有k个项目的候选项集即为Gi中第1列对应k个项目的集合，因此只需对Gi中对应的k行进行“与”操作即可计算含有k个项目的候选项集的局部支持度.在求k候选项集时，只需对最后一列大于k的行进行“与”操作即可，可以大大减少候选项集的数量.利用局部剪枝性质，删除局部支持度小于局部支持度阈值的项.

(5) 利用ReduceByKey操作，求得候选项集的全局支持度.如果全局支持度大于支持度阈值的项直接加入频繁项集集合L；如果全局支持度小于支持度阈值的项利用全局剪枝性质，再次扫描数据库，最终求得频繁项集的集合L.

1.2AMRDD算法描述

输入：数据集D(以数据块的形式存储在Hadoop的分布式文件系统中)，最小支持度阈值min_sup；

输出：D中的频繁项集的集合L.

(1)求L1

instans = sc.textfile(D)

L1= instans.map(_，1).reduceByKey(_ + _).filter(_ > min_sup)

(2)构造局部矩阵

Matrix G =∅；//初始化H×(J+2)矩阵

foreach(1 inL1)

foreach(tinDi)

if(1 int)

G.add(1) //若L1中的项l在事务t中，则相应位置1

else

G.add(0) //否则，相应位置0

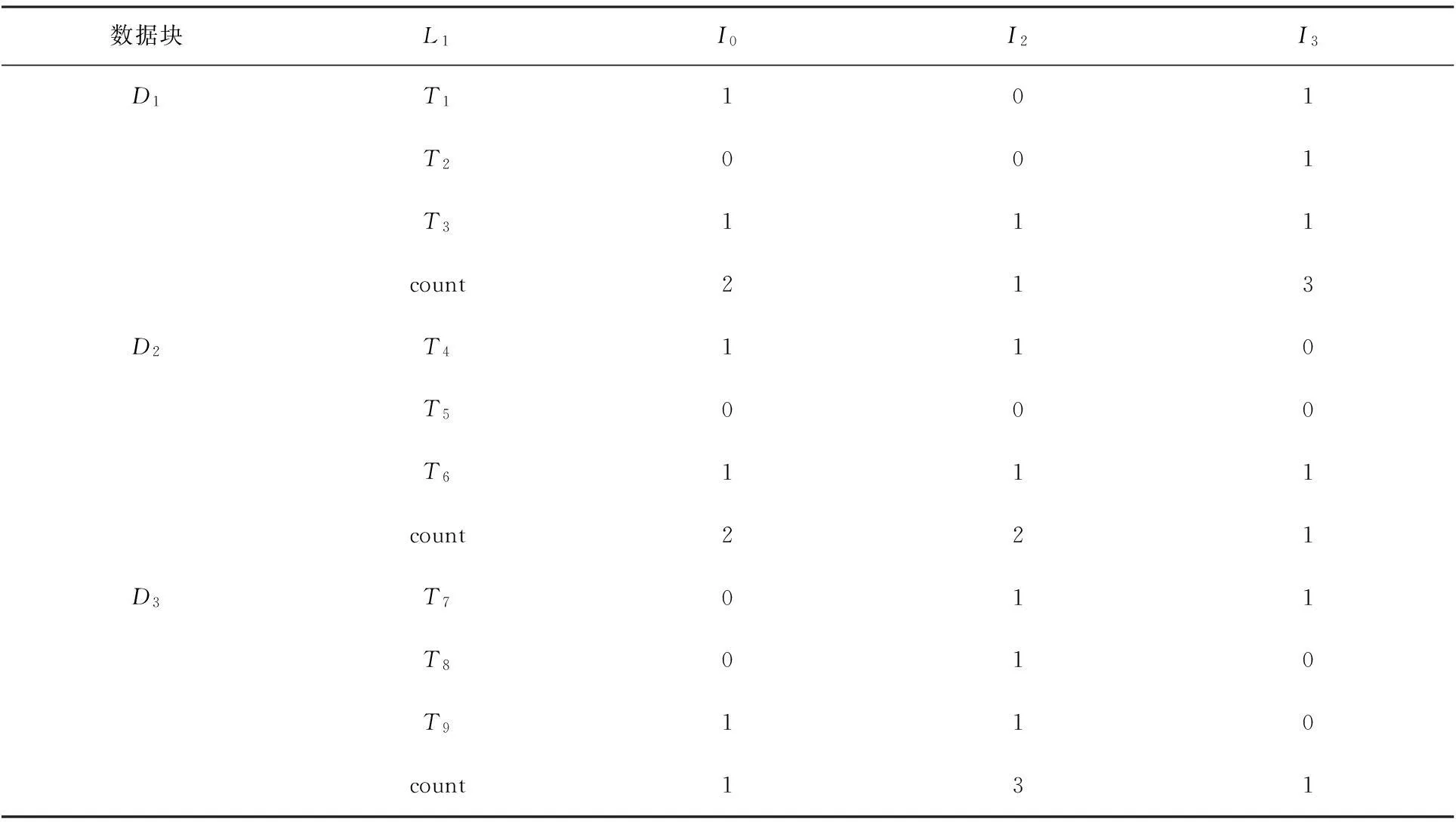
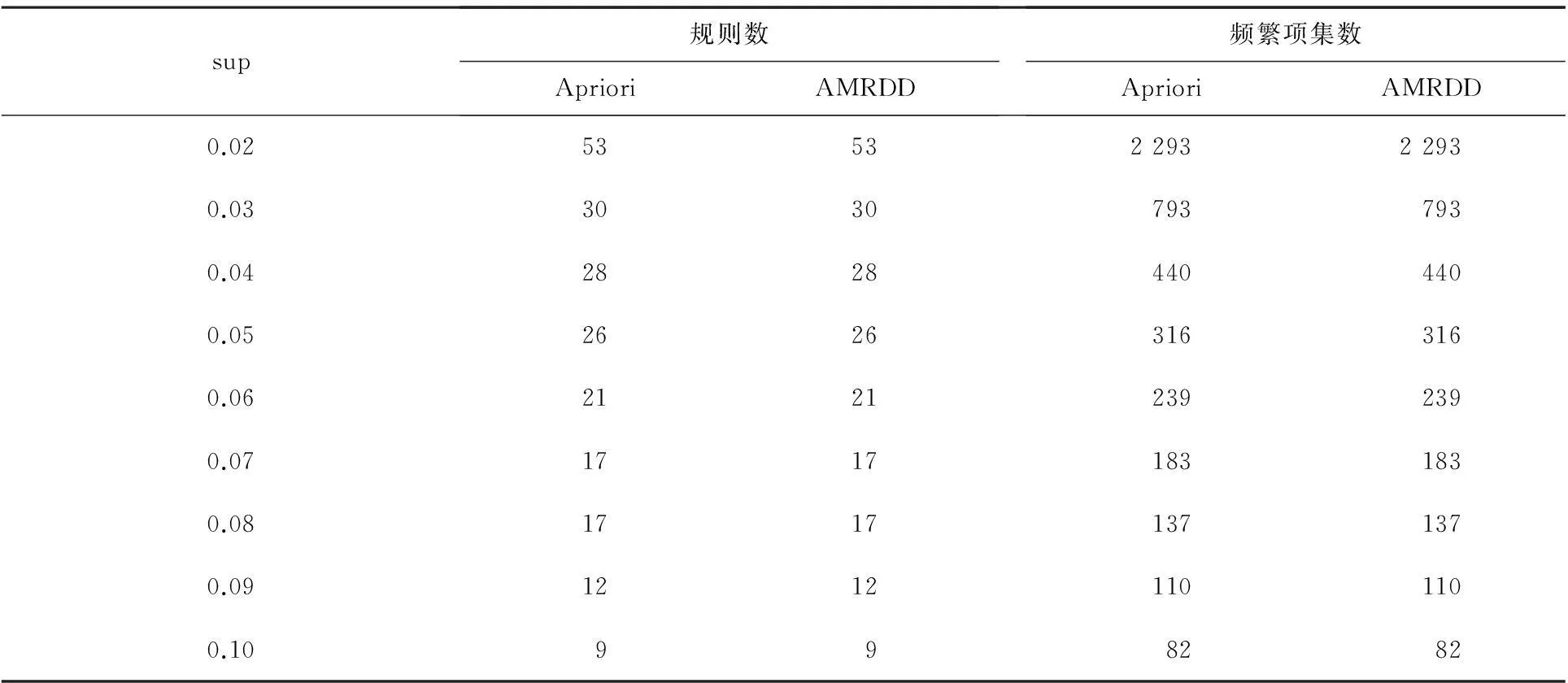
(3)求局部候选项集

for(1

for(0=

count=0

for(m

while(count

if(G[m][maxL-1]

break

else

count += 1

}

local_sup_count = [use“AND” operation on ‘kcolumn items’ of G]；

Ck.add()

}

}

}

(4)计算全局支持度，得到频繁项集L

对全局支持度小于最小支持度的项应用全局剪枝策略，遍历事务数据库进行剪枝

gCk=Ck.reduceByKey(_ + _).filter(_.2 < min_sup)

L= instans.map(_，gCk).reduceBykey(_ + _).filter(_ > min_sup) //全局支持度大于最小支持度的项直接加到频繁项集集合

L+=Ck.reduceByKey(_ + _).filter(_.2 > min_sup).add(kitems，sup_count)

returnL

2实验结果

实验环境为3台CPU Intel Core4、主频2.3 GHz、4 G内存，操作系统为CentOS6.5台式机，其中1台为master节点，同时也作为worker节点，另外2台为worker节点，通过交换机组成一个局域网.所用软件为JDK1.7、Hadoop2.4.0、Scala2.10.4、Spark1.1.0和IntelliJ13.6.实验数据采用IBM数据库生成器随机生成数据.

2.1算法有效性验证

采用图1中的事务数据，对AMRDD算法有效性进行验证，事务数据库D有9条交易记录D={T0，T1，T2，T3，T4，T5，T6，T7，T8}，I为项目集合，且I={I0，I1，I2，I3，I4，I5，I6}.假定数据被分成3个数据块D1={T0，T1，T2}，D2={T3，T4，T5}，D3={T6，T7，T8}，最小支持度阈值为4.传统Apriori算法和AMRDD算法挖掘这3块数据文件进行算法有效性验证.

AMRDD算法生成频繁1项集L1.以T0为例，产生键值对〈I0，1〉，〈I3，1〉，〈I5，1〉.同样，其他交易记录也将产生相应键值对.合并相同的key，可得到L1：{〈I0，5〉〈I2，6〉〈I3，5〉}.

构造局部矩阵.根据L1，通过扫描数据块将每条交易记录转化为一个列向量v.若一条交易记录中的项在L1中，则相应位值为“1”，否则为“0”.表1展示了3个数据块的列向量表示.

表1　数据块D1，D2和D3的列向量表示

以D1为例计算局部支持度local_sup.由表1可看出，I2的count计数为1<4/3，因此求候选项集进行“与”运算时忽略此行，候选项集为{I0I3}，则{I0I3}的局部支持度local_sup=1×1+1×0+1×1=2；用同样方法可计算D2，则{I0，I2}局部支持度分别为2，而D3由于count均小于4/3，因此没有生成候选项集，最后计算全局支持度.将候选项集局部支持度相加，得到{I0，I2}，{I0，I3}的全局支持度都为2，均小于最小支持度阈值，故运用全局剪枝策略再次扫描事务数据集，得到频繁项集L1：{〈I0，5〉〈I2，6〉〈I3，5〉}，L2：{〈I0I2，4〉}，符合要求的关联数据是I0和I2.传统Apriori算法生成的频繁项集L1：{I0I2I5}，L2：{I0I2，4}，符合要求的关联数据是I0和I2.从最终结果可以看出，AMRDD算法与传统Apriori算法挖掘出的频繁项集和关联规则结果及数量是一致的，证明了AMRDD算法没有丢失相关挖掘数据，算法改进后是有效的.

2.2算法支持度实验

对Apriori算法支持度设定不同也会影响算法的执行效率和产生的规则条数，若设定支持度太高，挖掘出的知识量可能有限，若支持度设定太低，将使算法运算复杂，也会产生一些无用冗余的规则.对传统Apriori算法和改进的AMRDD算法在设定不同支持度情况下挖掘的关联规则条数进行实验，结果如表2所示.

由表2可以看出，当sup=0.07和sup=0.08时产生的规则数一样多，但是sup=0.08时明显比sup=0.07时产生的频繁项集数目少，由此可见选择合适的支持度既可以产生适当的规则数，也可以缩短算法的运行时间，从而提高了效率.

表2　不同支持度算法输出结果

2.3算法数据分块实验

数据集的大小对算法的运行效率有一定影响，划分的数据块过大，每个运算节点的计算量和负载则加大，影响算法效率，若划分的数据块小，数据集分块多，则运算节点间通信压力变大，也同样会影响算法的运算效率，所以实验将数据集分成1，2，3，4，5，6，7，8，9块数据进行挖掘，实验效果如图2所示.由图2可看出，随着数据分块数增多，程序运行时间不断下降，数据块为4的时候，运行时间最短，之后随着数据分块数增加运行时间也不断增加.因此，数据分块是影响算法效率的一个因素.

2.4不同数据量下算法运行时间实验

实验分别实现了单机的Apriori算法、Hadoop平台上的MRApriori算法和Spark平台上的AMRDD算法.在不同大小的数据集上，不同算法的运行时间比较见图3.

图2　不同数据分块下运行时间比较

图3　不同算法运行时间比较

由图3可看出，当数据量小于百万条时，基于Spark和Hadoop的算法与传统Apriori算法所用的时间相差不多，随着数据量增加，时间差逐渐增大.这是因为当数据量逐渐增大时，基于Spark平台和Hadoop平台数据处理时间比例上升，通信开销所占比例逐渐缩小，甚至可以忽略.当数据量继续增大时，AMRDD算法比MRApriori算法有明显的优势，产生这种现象的原因是Spark可以将计算的中间结果cache存到内存中，省去了MapReduce大量的磁盘I/O操作.

3总结

本文在传统Apriori算法的基础上提出了AMRDD算法，该算法引入矩阵概念，应用了局部剪枝策略和全局剪枝策略从而大大减少了生成候选项集的数量，并充分利用Spark的并行化优点，迭代计算基于内存，比Hadoop更快.实验结果表明，传统Apriori算法不适合处理大数据，基于Spark的算法明显优于基于Hadoop的算法.将传统的数据挖掘算法移植到Spark平台上来处理大数据将会是未来的一个趋势.

[参考文献]

[1]李锋刚，梁钰. 基于LDA-wSVM模型的文本分类研究[J]. 计算机应用研究，2015，32(1)：21-25.

[2]宋天勇，赵辉，李万龙，等. 引入自检策略的进化K-means算法[J]. 东北师大学报(自然科学版)，2014，46(3)：59-63.

[3]柴玉梅，张卓，王黎明. 基于频繁概念直乘分布的全局闭频繁项集挖掘算法[J]. 计算机学报，2012，35(5)：990-1001.

[4]冯勇，尹洁娜，徐红艳. 基于垂直频繁模式树带有负载均衡的分布关联规则挖掘算法[J]. 计算机应用，2014，34(2)：396-400.

[5]CHANCHAL YADAV，SHULIANG WANG，MANOJ KUMAR. An approach to improve Apriori algorithm based on association rule mining[C]//2013 Fourth International Conference on Computing，Communications and Networking Technologies (ICCCNT)，USA：IEEE，2013:1-9.

[6]杨新月. 云计算环境下关联规则算法的研究[D]. 成都:电子科技大学，2011.

[7]毛卫俊. 基于云平台的并行关联规则挖掘算法研究[D]. 上海:华东理工大学，2014.

[8]MOHAMMADHOSSEIN BARKHORDARI，MAHDI NIAMANESH. ScadiBino an effective MapReduce-based association rule miming method[C]//ICEC’14：Proceedings of the Sixteenth International Conference on Electronic Commerce，Philadelphia：ICEC，2014:1-8.

[9]MATEI ZAHARIA，MOSHARAF CHOWDHURY，TATHAGATA DAS，et al. Resilient distributed datasets：a fault-tolerant abstraction for in-memory cluster computing[C]// Presented as part of the 9thUSENIX Symposium on Networked Systems Design and Implementation，USA：Matei University of California，2012：25-27.

(责任编辑：石绍庆)

The improvement and research of Apriori algorithm based on Spark

NIU Hai-ling，LU Hui-min，LIU Zhen-jie

(School of Computer Science and Engineering，Changchun University of Technology，Changchun 130012，China)

Abstract:The AMRDD algorithm is proposed on the basis of the traditional Apriori algorithm，which is a distributed association rules algorithm based on Spark. To reduce the times of scanning the database，the matrix is introduced，and the number of candidate frequent itemsets is reduced by using local pruning strategy and global pruning strategy. The algorithm is realized on Spark platform，and compare with the traditional Apriori algorithm and the Apriori algorithm based on Hadoop. The experimental results show that AMRDD algorithm performs effectively on big data for mining frequent itemsets.

Keywords:Apriori；Spark；matrix；local pruning strategy；global pruning strategy

[中图分类号]TP 391[学科代码]520·20

[文献标志码]A

[作者简介]牛海玲(1985—)，女，硕士研究生； 通讯作者：鲁慧民(1972—)，女，博士后，副教授，主要从事智能信息处理、大数据研究.

[基金项目]国家自然科学基金资助项目(61472049)；吉林省自然科学基金资助项目(20130101055JC)；吉林省科技发展计划项目(20150204005GX)；长春市重大科技攻关计划项目(14KG082).

[收稿日期]2015-05-08

[文章编号]1000-1832(2016)01-0084-06

[DOI]10.16163/j.cnki.22-1123/n.2016.01.018