具有饱和接触率的随机SIR模型的正解存在唯一性及灭绝性

张秋梅，文香丹，李映红

(1.长春大学理学院，吉林 长春 130022；

2.延边大学数学系，吉林 延吉 133002)



具有饱和接触率的随机SIR模型的正解存在唯一性及灭绝性

张秋梅1，文香丹2，李映红1

(1.长春大学理学院，吉林 长春 130022；

2.延边大学数学系，吉林 延吉 133002)

[摘要]建立并分析了具有饱和接触率的随机SIR模型，应用Lyapunov方法得到了随机SIR模型正解的存在性、唯一性和灭绝性.

[关键词]随机微分方程；饱和接触率；存在唯一性；灭绝性

0引言

自从Kermack和Mckendrick建立传染病的舱室模型后，传染病动力学便得到了迅速发展，并在预防与治疗疾病方面起到了不同程度的指导作用. 基于经典的假设，我们将种群分成易感者(S)，染病者(I) 和移出者(R). 一个易感个体一旦感染便瞬间变成染病者，最后成为移出者获得暂时的免疫.[1-3]如果疾病的发生率是饱和接触率，则SIR模型可描述为

(1)

(2)

本文研究每次接触传染的概率β在环境白噪声干扰下的随机传染病系统(SIR)正解的存在唯一性及灭绝性.

1正解的存在唯一性

证明考虑具有初值(u0=logS0，v0=logI0，w0=logR0)的如下方程

(3)

显然方程(3)的系数满足局部Lipschitz条件，从而存在唯一局部解(u(t)，v(t)，w(t))(t∈[0，τe))，其中τe表示爆破时间.由It公式容易验证(S(t)=eu(t)，I(t)=ev(t)，R(t)=ew(t))是系统(2)具有初值(S0，I0，R0)的正解.下面证明解是全局存在的，即只需证明τe=∞ a.s..选取m0≥1，使得S0，I0，R0都位于区间中.对任给整数m≥m0，定义停时：或max{S(t)，I(t)，R(t)}≥m}，其中约定inf∅=∞.显然τm关于m单调递增，令，则τ∞≤τea.s..若能证得τ∞=∞ a.s.，则τe=∞，从而定理结论得证.若不然，则存在常数T>0和ε∈(0，1)，使得P{τ∞≤T}>ε.于是存在整数m1≥m0，使得当所有的m≥m1时，P{τm≤T}≥ε.

2灭绝性

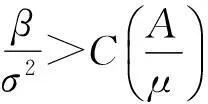
(4)

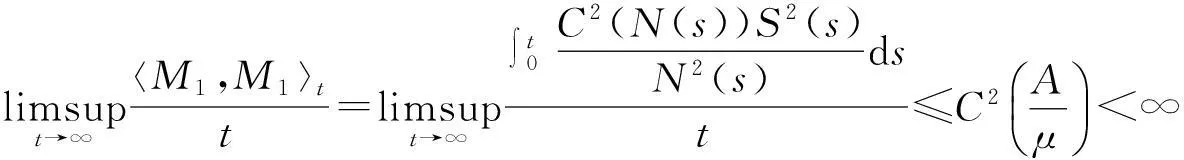
由强大数定律[8]得

再根据(4)式

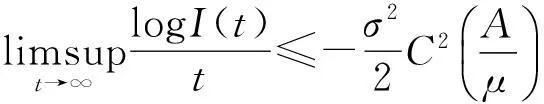
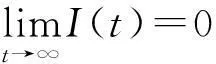
(5)

根据系统(2)

d(S+I+R)=[A-μ(S+I+R)-α0I]dt.

(6)

由(6)式解得

利用洛必达法则和(5)式，

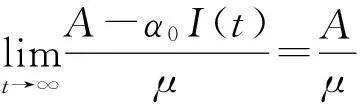
[参考文献]

[1]ZHANG J，MA Z E.Global dynamics of an SEIR epidemic model with saturating contact rate [J].Mathematical Biosciences，2003，185：15-32.

[2]马知恩，周义仓，王稳地，等.传染病动力学的数学建模与研究[M].北京：科学出版社，2004:156-160.

[3]王冰杰.基于潜伏期有传染力的SEIR传染病模型的控制策略[J].东北师大学报(自然科学版)，2014，46(1):28-32.

[4]YANG Q S，JIANG D Q，SHI N Z，et al.The ergodicity and extinction of stochastically perturbed SIR and SEIR epidemic models with saturated incidence[J].J Math Anal Appl，2012，388：248-271.

[5]JI C Y，JIANG D Q，YANG Q S，et al.Dynamics of a multigroup SIR epidemic model with stochastic perturbation [J].Automatica，2012，48：121-131.

[6]JI C Y，JIANG D Q，SHI N Z.Multigroup SIR epidemic model with stochastic perturbation[J].Physica A，2011，390：1747-1762.

[7]ZHAO Y N，JIANG D Q，O’REGAN D.The extinction and persistence of the stochastic SIS epidemic model with vaccination[J].Physica A，2013，392：4916-4927.

[8]MAO X R. Stochastic differential equations and their applications[M]. Chichester：Horwood Publishing，1997：51-59.

(责任编辑：李亚军)

Existence，uniqueness and extinction of stochastic SIR model with saturating contact rate

ZHANG Qiu-mei1，WEN Xiang-dan2，LI Ying-hong1

(1.School of Science，Changchun University，Changchun 130022，China；2.Department of Mathematics，Yanbian University，Yanji 133002，China)

Abstract:A perturbed SIR model with saturating contact rate by white noise is proposed and analyzed. By Lyapunov analysis methods，the existence and uniqueness of the positive solution are given，as well as the extinction of stochastic SIR model.

Keywords:stochastic differential equation；saturating contact rate；existence and uniqueness；extinction

[中图分类号]O 211.63[学科代码]110·44

[文献标志码]A

[作者简介]张秋梅(1980—)，女，博士，讲师，主要从事随机微分方程研究；通讯作者：文香丹(1965—)，女，硕士，教授，主要从事应用概率统计和优化理论研究.

[基金项目]国家自然科学基金资助项目(11371085)；吉林省自然科学基金资助项目(20140101005JC)；吉林省教育厅“十二五”科学技术研究项目(2014LY508L40，吉教科合字[2015]第10号)；吉林省教育科学“十二五”规划课题项目(GH150104).

[收稿日期]2014-07-23

[文章编号]1000-1832(2016)01-0026-03

[DOI]10.16163/j.cnki.22-1123/n.2016.01.007