图(s〈C4，3〉)∪Pm的优美性

吴 跃 生

(华东交通大学理学院，江西 南昌 330013)



图(s〈C4，3〉)∪Pm的优美性

吴 跃 生

(华东交通大学理学院，江西 南昌 330013)

[摘要]研究了图(s〈C4，3〉)∪Pspan的优美性，证明了当s为大于等于2的自然数，m为任意正整数时，图(s〈C4，3〉)∪Pspan是优美的.其中图〈C4，3〉是将3个C4中每个C4的一个顶点粘接到一起得到的新图，Pspan是有m+1个顶点的路，而(s〈C4，3〉)∪Pspan是s个〈C4，3〉与一个Pspan的非连通并.文中所得结果部分解决了已有文献给出的猜想.

[关键词]优美图；交错图；非连通图；路

1预备知识

优美图因其应用性和趣味性，引起众多学者的广泛研究.[1-10]文献[7-8]研究了图(s〈C4，n〉)∪Pm的优美性，文献[7]中还给出了如下猜想：∀m，n，∀s≥2，图(s〈C4，n〉)∪Pm是优美的.本文证明了当n=3时，此猜想成立.

定义1[1]对于一个图G=(V，E)，若存在一个单射

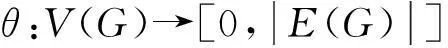
使得对所有边e=uv∈E(G)，由

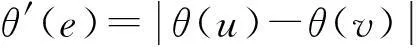
定义2[2]设θ是图G的优美标号，

V(G)=X∪Y，X∩Y=∅.

如果

则称θ是G的交错标号，称G是在交错标号θ下的交错图，称k为交错图G关于交错标号θ的特征.

定义3[7-8]指定图C4的一个顶点为根，将n个C4的根粘在一起得到的图记为〈C4，n〉，粘结点记为b，则称〈C4，n〉中的每个C4为分支.Pm是有m+1个顶点的简单通路，图(s〈C4，n〉)∪Pm是s个〈C4，n〉与一个Pm的非连通并.

2主要结果及其证明

引理1[5]设路Pm=v0v1v2…vm.∀a∈{0，1，2，…，m}，路Pm存在一个优美标号θ，使得θ(v0)=a.

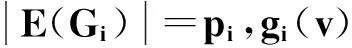
V(Gi)=(Xi，Yi)，

引理3[8]当n>2时，非连通图2〈C4，n〉存在特征为4n，缺4n+2和8n-1标号值的交错标号.

引理4[11]当T为优美树时，设T⊙K1是优美树T中优美值为1的顶点粘接一条悬挂边后所形成的树，则非连通图Gk+2∪T⊙K1是优美图；当T为交错树时，设T的交错标号θ1的特征为k1，(X1，Y1) 是T的二分划，

则非连通图Gk+2∪T⊙K1是交错图.

引理5非连通图3〈C4，3〉存在特征为18，缺20和35标号值的交错标号.

证明如图1所示，非连通图3〈C4，3〉存在特征为18，缺20和35标号值的交错标号.

定理1当s≥2为自然数，m为任意正整数时，非连通图(s〈C4，3〉)∪Pm是优美的.

证明由引理1—引理5即可推出本定理结论.

例1非连通图(3〈C4，3〉)∪P3的交错标号如图2所示.非连通图(3〈C4，3〉)∪P5的优美标号如图3所示.

引理6(ⅰ) 如果T为优美树，且T⊙K1是优美树T中优美值为2的顶点粘接一条悬挂边后所形成的树，则非连通图Gk+3∪T⊙K1是优美图；

(ⅱ) 如果T为交错树，设T的交错标号θ1的特征为k1，(X1，Y1)是T的二分划，

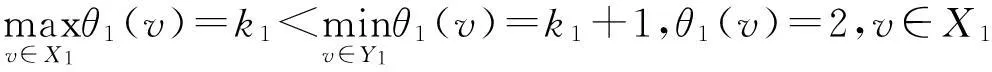
则非连通图Gk+3∪T⊙K1是交错图.

证明(ⅰ) 设树T的优美标号为θ1，θ1(v1)=2.在v1处粘接的一条悬挂边为v1v2，顶点v2为悬挂点(或叶)，

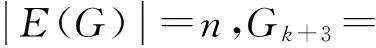
定义非连通图Gk+3∪T⊙K1的标号θ2如下：

下面证明θ2是非连通图Gk+3∪T⊙K1的优美标号.

(1) 映射

θ2:V(Gk+3)→[0，k]∪[k+4+m，m+n]∪{k+1+m，k+2+m}

是单射，映射

θ2:V(T⊙K1)→[k+1，k+m]∪{k+m+3}

也是单射，所以映射

θ2:V(Gk+3∪T⊙K1)→[0，n+m]

是单射.

(2) 映射

是双射.

由优美标号的定义可知θ2是非连通图G∪T⊙K1的优美标号.

(ⅱ) 当T为交错树时，令

X2=X1∪X，

Y2=Y1∪Y∪{v2}，

则由已知条件有

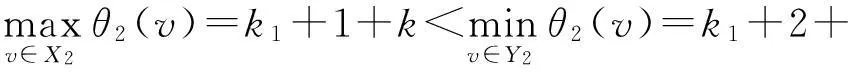
即θ2是非连通图G∪T⊙K1的交错标号，此交错标号的特征为k1+1+k.证毕.

引理7图〈C4，3〉存在特征为3，缺6标号值的交错标号.

证明图4为〈C4，3〉的交错标号，由图4可知引理结论正确.

图4　图〈C4，3〉的交错标号

定理2当m为大于等于2的自然数时，〈C4，3〉∪Pm是优美的.

证明由引理1，引理6和引理7即可推出本定理结论.

例2非连通图〈C4，3〉∪P4的交错标号如图5所示.非连通图〈C4，3〉∪P6的优美标号如图6所示.

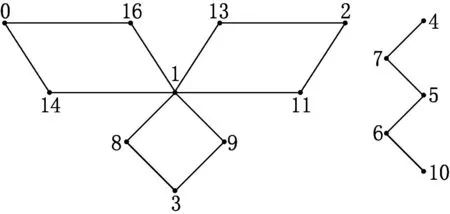
图5　图〈C4，3〉∪P4的交错标号

图6　图〈C4，3〉∪P6的优美标号

[1]马克杰.优美图[M].北京：北京大学出版社，1991：1-247.

[2]杨显文.关于C4m蛇的优美性[J].工程数学学报，1995，12(4):108-112.

[3]吴跃生.非连通图C4m-1∪G的优美标号[J].吉首大学学报(自然科学版)，2014，35(3):1-3.

[4]吴跃生.再探非连通图C4m-1∪G的优美标号[J].吉首大学学报(自然科学版)，2015，36(1):1-4.

[5]FLANDRIN E，FOURNIER I，CERMA A.Numotations gracieuses des chemins[J].Ars Combin，1983，16:149-181.

[7]张志尚，张庆成，王春月.关于(s〈C4，n〉)∪Pm的优美性[J].东北师大学报(自然科学版)，2011，43(3)：14-18.

[8]杜万根.关于(s〈C4，n〉)∪Pm的优美性[J].苏州大学学报(自然科学版)，2012，28(2):7-11.

[9]FRUCHTRW，SAUNASLC.Gracefulnumheringofsnakeswithconstantsonthefirst1abe1[J].ArsCombin，1985，20：143-157.

[10]GALLIAN J A. A dynamic survey of graph labeling[J/OL].The Electronic Journal of Combinatorics，2014[2014-05-23].http://www.combinatorics.org/ojs/index.php/eljc/article/view/DS6.

[11]吴跃生，王广富，徐保根.非连通图G∪T⊙K1的优美性[J].东北师大学报(自然科学版)，2014，46(1)：14-16.

(责任编辑：李亚军)

On the gracefulness of (s〈C4，3〉)∪Pm

WU Yue-sheng

(School of Science，East China Jiaotong University，Nanchang 330013，China)

Abstract:This article deals with the gracefulness of graph (s〈C4，3〉)∪Pspanand proves that (s〈C4，3〉)∪Pspanis graceful when s≥2(s and m are positive integer)，where the graph 〈C4，3〉 is achieved by identifying a vertex of each C4 of 3C4s with one vertex，graph Pspanis the path with m+1 vertexes，and graph (s〈C4，3〉)∪Pspanis the disjoint union of (s〈C4，3〉)s and Pspan.

Keywords:graceful graph；alternating graph；unconnected graph；path

[中图分类号]O 157.5[学科代码]110·7470

[文献标志码]A

[作者简介]吴跃生(1959—)，男，硕士，副教授，主要从事图论研究.

[基金项目]国家自然科学基金资助项目(11261019，11361024).

[收稿日期]2014-05-23

[文章编号]1000-1832(2016)01-0018-04

[DOI]10.16163/j.cnki.22-1123/n.2016.01.005