基于非线性回归的制动盘通风道结构优化*
郑伟奇,康 宁,刘献栋,胡立中
(1.北京航空航天大学交通科学与工程学院,北京 100191; 2. 东风汽车公司技术中心,武汉 430058)
2016213
基于非线性回归的制动盘通风道结构优化*
郑伟奇1,康 宁1,刘献栋1,胡立中2
(1.北京航空航天大学交通科学与工程学院,北京 100191; 2. 东风汽车公司技术中心,武汉 430058)
为提高通风制动盘的散热能力,对其内部通道形式进行了优化。根据正交试验设计提出16种通道布置方案,利用CFD方法计算各方案的内壁散热功率。通过方差分析确定各因素影响通风盘散热的显著性水平。忽略非显著性因素后,利用非线性回归方法建立了以通道数量、入口角度和散热肋截面特征为自变量的制动盘内壁散热功率计算模型。采用遗传算法寻求该模型的最优解,得到最优通道形式为80条通风道、通道入口与出口角度均为20°和4号散热肋。CFD计算结果表明,该最优通道结构内壁散热功率为10.465kW,比正交表中各方案的最低散热功率高1倍,比表中最高散热功率高1.62%,说明优化后得到的通风道结构能有效提高制动盘的散热能力。
通风制动盘;对流散热;优化;正交试验设计;非线性回归
前言
当车辆进行紧急制动、频繁制动或长下坡制动时,制动盘的温度会急剧升高。这容易导致制动失效和轮胎起火等严重事故的发生[1]。因此,制动盘能够快速降温是汽车安全行驶的重要保证。防止制动盘温度过高的常用手段是在其内部设置通风通道。不同形式的通风道散热效率相差很大。为最大程度提高制动盘的散热能力,对通道结构进行优化研究具有重要意义。
径向长直通道是一种最基本的通道形式。无论制动盘转速和通道长度等参数如何变化,其内部总存在着相似的湍流结构,例如入口端的流动分离和背风面的涡流[2-3]。这些流动现象都严重制约着通道的散热效果。为了改善通道内部流场,文献[4]~文献[6]中对径向直通道进行了一些简单的改进:将散热肋入口端面倒圆角,使之能尽量避免进入通道的气流发生分离;或将直通道设计成与径向呈一定角度,能有效缩小回流区域;亦或用螺旋槽壁面替换光滑内壁,以增加通道内壁附近的湍流强度。弯曲通道是另一种常见的通风结构,不同曲率的弯曲通道内部湍流形态相差巨大[7]。弯曲通道又可分为前向和后向弯曲两种形状。后向弯曲通道最有利于制动盘散热,其次是前向弯曲通道,再次是径向直通道。故在通风道设计时应优先采用后向弯曲的结构形式[8-9]。研究发现,对流换热面积是影响制动盘冷却效率的关键因素[10]。文献[11]~文献[13]中试图通过在通道内部增设短肋或将整条散热肋分割成若干段的方法来增加对流换热面积,从而提高制动盘散热效率。对于前种方法,当短肋被安置在通道出口端时效果最好;对于后者,散热肋被间隔成3段时,通风道散热能力提升幅度最大。
在以上研究中,均默认散热肋宽度沿径向保持不变。而本文中考虑了散热肋入口端宽度与出口端宽度不相等的情况,将散热肋截面特征纳入考察因素。本文中的通道均为样条曲线形状,其弯曲程度可由入口角度、出口角度确定。因此,最终选取通道数量、通道入口、通道出口和散热肋截面形状作为考察因素,进行了4因素、4水平的正交试验方案设计。正交试验方案的CFD仿真结果和方差分析揭示了通道数量、通道入口、出口角度和肋形对制动盘散热的影响和影响程度的大小顺序。据此,建立了制动盘内壁散热功率非线性回归模型,并采用遗传算法进行优化,得到了最优通道形式。最后,对该最优通道结构进行了计算验证和流场分析。
1 物理模型与正交方案
本文中研究的制动盘物理模型由某款常见的圆弧通道制动盘简化而来,其结构示意图如图1所示。图中a1,a2,w1和w2分别代表通风通道入口角度、出口角度、散热肋入口端宽度和出口端宽度。制动盘绕Z轴旋转。

图1 通风制动盘结构示意图
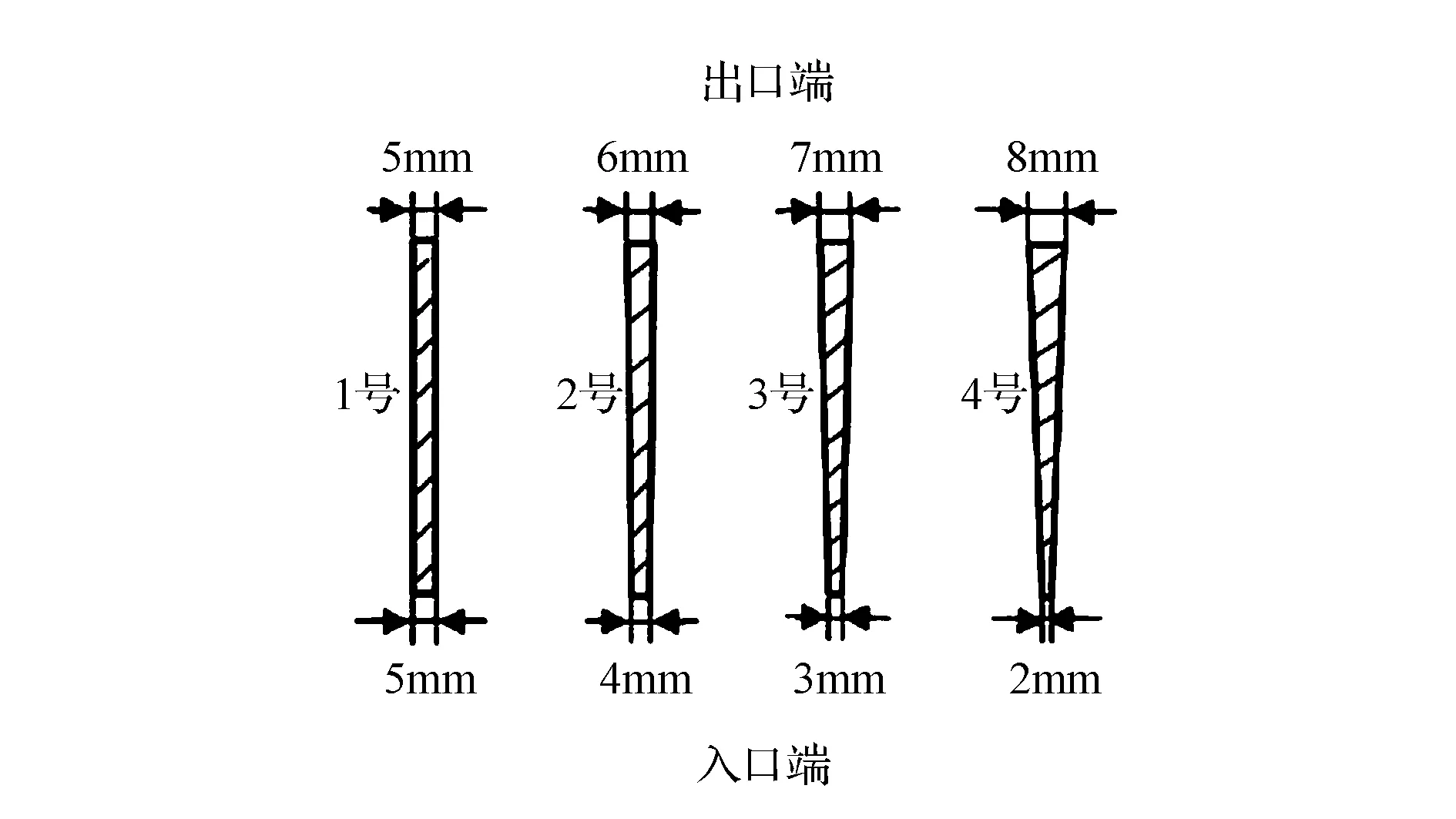
图2 4种类型散热肋截面示意图
根据L16(45)正交表将以上4个因素和各自的4个水平编排成16种通道结构方案,多余的空白列可作为误差列,参与方差分析。最终确定的通道结构正交方案如表1所示。接下来需要利用CFD方法对每组方案的内壁散热功率进行计算,用以衡量不同通风结构的散热能力。
2 数值计算方法与验证
2.1 数值计算方法
考虑到制动盘为各通风道完全相同的轴对称结构,故只须选取包含一条通道的周期性单元作为研究对象。忽略制动盘内部的热传导后,可将制动盘实体视为非计算域。为应用MRF方法模拟制动盘旋转,在紧邻制动盘外缘2mm处建立封闭的旋转计算域。经过对不同大小的空气域进行尝试后,最终确定空气计算域的尺寸为外径R=320mm、高度H=302mm。各计算域如图3所示。
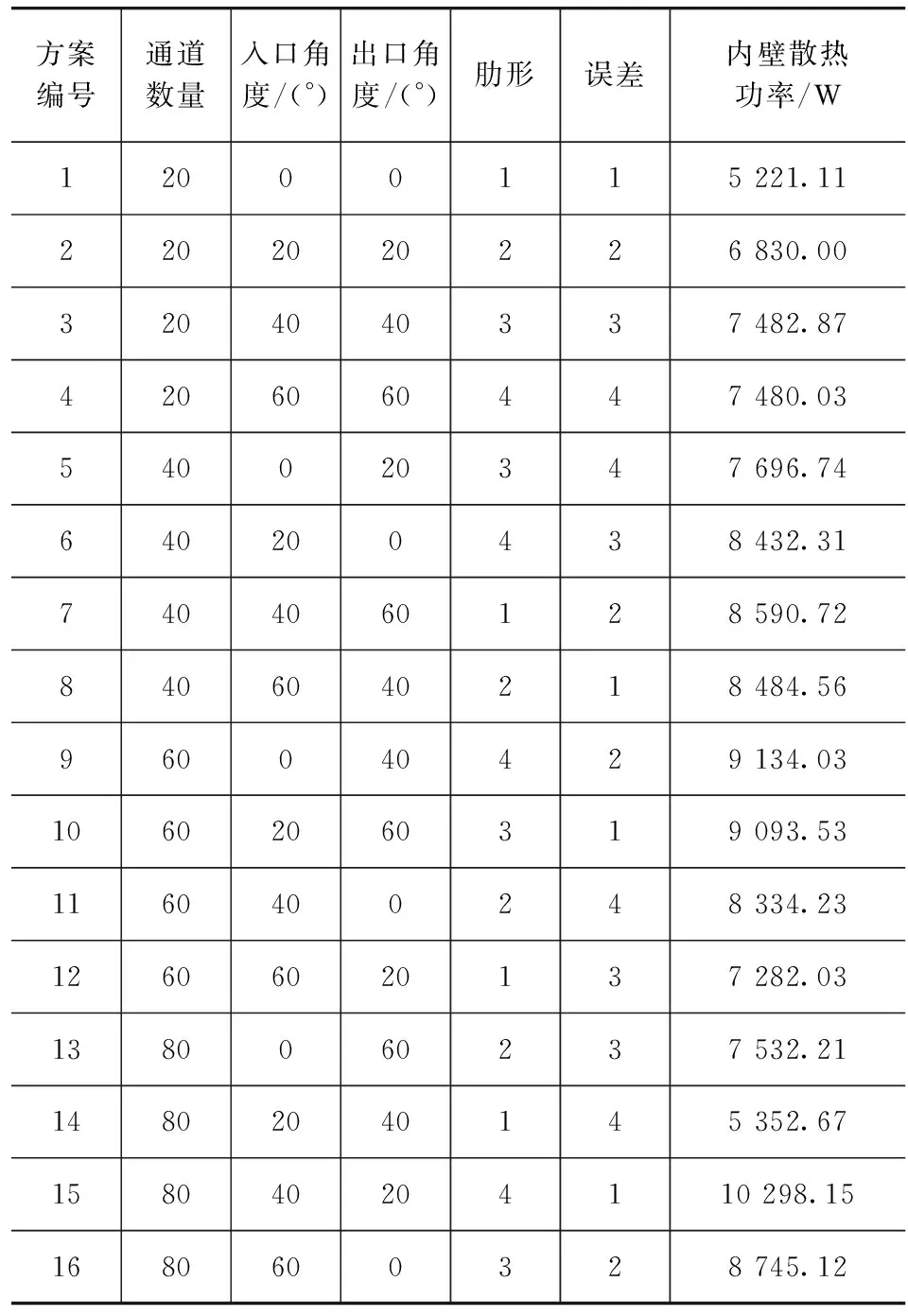
表1 通道结构正交方案

图3 计算域
在空气计算域和旋转计算域内生成结构网格,经过网格无关性分析后确定单元总数在68万左右。此时制动盘壁面第1层网格高度为0.5mm,尺寸放大系数为1.1。网格划分如图4所示。

图4 网格划分
通风制动盘散热可视为三维定常不可压流动传热问题,满足如下控制方程。
连续方程:
传统的成本管理过分强调“省”和“节流”,努力追求成本最小化,结果使成本管理仅仅限制在生产领域当中,这种方式把直接材料、直接人工,和制造费用当作减少成本费用的主要技巧,因此成本管理陷入了一个简单的循环,成本的减少并不能够提供最终的决策所需要的有效信息,无法准确的表现出整个经营活动过程,更不能具体的表现出每一个环节的成本信息。反而更多的关注点放在了生产过程中的节省,这样造成了在过程当中核算的比较多,但是前期的预测和准备较少,成本管理效果非常弱。
(1)
动量方程:
(2)
能量方程:
(3)
式中:ui为速度分量;p为压力;T为温度;μ为动力黏性系数;F为质量力;ρ为密度;Cp为定压比热;k为导热系数。
将空气的物性参数视为不随温度变化的常数,设定其密度为1.029kg/m3,定压比热值为1 009J/(kg·K),热传导系数为0.029 6W/(m·K),动力黏性系数为2.06×10-5kg/(m·s)。
在求解数值模型时,边界条件的设置如表2所示。将入口与出口的操作压强均设定为101 325Pa。空气域的顶面与底面设置为对称面边界条件是为了模拟空气在此处的自由滑移状态。制动盘的旋转角速度取值为138.89rad/s,相当于高速行驶的小轿车的车轮转速。

表2 边界条件
本文中选用SIMPLE算法求解压强-速度耦合方程,采用二阶迎风格式对动量方程与能量方程进行空间离散。根据经验,k-ε湍流模型适用于本文中的流动现象。整个计算过程持续5 000步即可收敛。
2.2 数值方法验证
文献[14]中对直径为0.83m、宽为0.25m、前进速度为9.592m/s的车轮的阻力系数进行了实验测量。为验证本文中数值方法的可靠性,利用本文中的方法对文献[14]中的实验过程进行仿真。将计算结果与实验结果进行比较,如表3所示。

表3 车轮阻力系数计算值与实验值
由表3可知,在静止与滚动情况下,计算值与实验值的相对误差分别为6.5%和6.9%。这种误差既可能来自实验测量,也可能来自模型的简化。但该误差足够小,可认为本文中的数值计算方法是可靠的。
3 方差分析

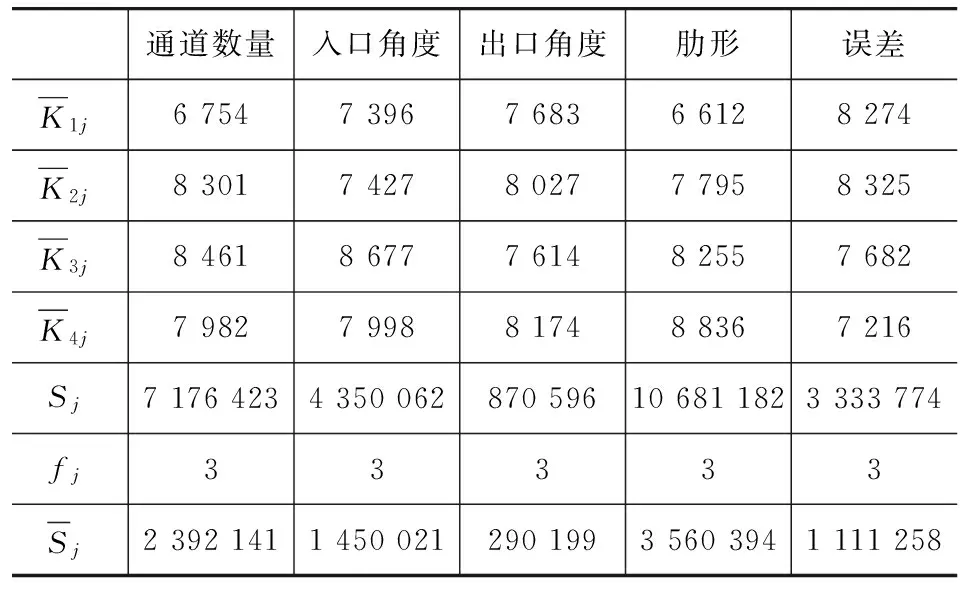
表4 分析计算表

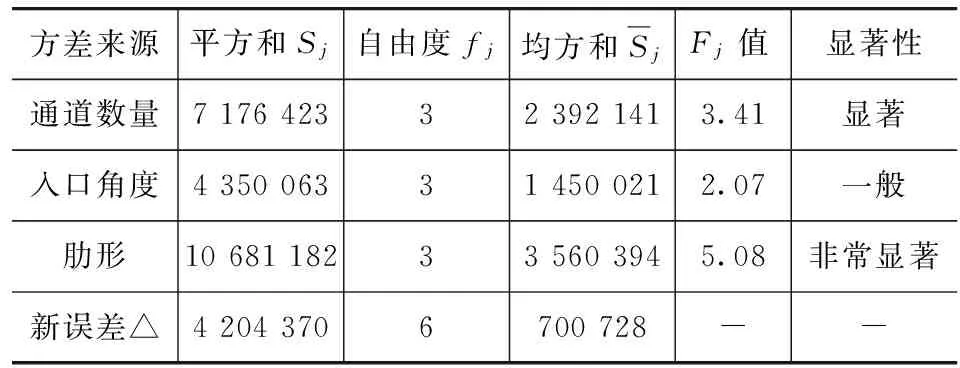
表5 方差分析表
完成正交方案的方差分析后,对各因素的影响显著性水平有了定量了解。各因素对通风盘散热能力影响显著性水平从高到低的排列顺序为肋形特征、通道数量、入口角度和出口角度。其中出口角度对制动盘散热能力的影响可以忽略。因此,接下来建立制动盘散热功率模型时,可忽略通道出口角度因素,只将散热肋截面类型、通道数量和通道入口角度视为自变量。
4 最优通道结构与流场分析
利用Matlab对表1中的正交数据进行非线性回归,得到制动盘内壁散热功率关于通道数量、通道入口角度和散热肋截面类型之间的三元二次方程为
式中:P为制动盘内壁散热功率;n为制动盘通风道数量,取整数且20≤n≤80;a1代表通风道入口角度,a1为整数且0≤a1≤60;t为散热肋截面类型编号,取1,2,3和4。

图5 样本值与预测值对比
利用遗传算法,在自变量的取值范围内求得该函数的最大值为10 473.3,此时n=80,a1=20,t=4。即通道数量为80,通道入口角度为20°,散热肋采用4号肋形时,制动盘散热能力达到最强。对于通道出口角度来说,由于其对制动盘散热的影响明显不显著,可以任意取值。本文中从制动盘质量尽量小、制造难度尽量低等方面考虑,将通道出口角度定为20°。至此,得到制动盘通道最优结构方案:采用4号散热肋在制动盘内部形成80条通道,并且通道入口与出口的角度均为20°。该最优设计不在正交表的已有方案中。为验证其最优性,需建立数值模型对其内壁散热功率进行仿真。利用本文中数值方法计算得到最优通道结构的内壁散热功率为10 465.34W,与制动盘内壁散热功率计算模型的预测值仅相差0.076%,这说明此回归模型是准确的。观察正交表中各方案的散热功率可知:方案1的通道结构形式散热能力最差,制动盘内壁散热功率仅为5 221.11W;方案15的散热能力最强,其制动盘内壁散热功率为10 298.15W。同正交表中的各方案相比,该最优通道结构形式的内壁散热功率均有所提高:相比于方案1,散热功率提高了1倍;相比于方案15,散热功率仍提高了1.62%。这说明其优化效果是可信的。
下面通过流场分析揭示最优通道结构能够提升散热能力的机理。图6为正交表中方案1与最优方案的通道内部空气流动迹线对比。对于方案1来说,不仅其通道入口处发生气流分离,而且散热肋背风面存在大面积的涡流区。而对于最优方案来说,其通道内部气流通畅,不存在回流区域。

图6 两种方案通道内部气流迹线
图7为方案1与最优方案的散热肋表面对流换热系数分布。从云图可以看出,方案1的散热肋迎风面对流换热系数整体上明显大于背风面,迎风面与背风面的平均对流换热系数为71.55W/(m2·k)。最优方案中散热肋迎风面与背风面的对流换热系数分布特征基本相同,平均对流换热系数为106.56W/(m2·k),比方案1大48.93%。

图7 两种方案散热肋表面对流换热系数分布
对比图6和图7可以发现,对流换热系数分布特点与流场的分布特点直接相关联。发生分离和回流的区域对流换热系数较小,这是因为涡流极不利于空气流通,严重阻碍了热量的交换。总体来说,相比于方案1,最优方案的结构形式能够大大改善通道内部流场,从而大幅提升制动盘内壁散热功率。
5 结论
本文中以制动盘内壁散热功率最大化为目标,将散热肋形状特征考虑在内,对制动盘的通道结构进行优化研究后得到了以下结论。
(1) 肋形因素和通道数量对制动盘散热能力的影响分别是非常显著和显著的,通道入口角度对制动盘的散热能力只有一般影响,而通道出口角度对制动盘散热的影响则是可以忽略的。
(2) 制动盘内壁散热功率与通道数量、通道入口角度以及肋形之间符合三元二次非线性关系。在自变量的取值范围内,可以根据给定的散热肋截面类型、通风道数量、通风道入口角度准确预测相应的制动盘内壁散热功率。
(3) 散热效果最佳的通道结构为:80条通风道,通道入口角度和出口角度均等于20°,4号肋形。该最优通道结构形式能使制动盘内壁散热功率达到10.465kW,比正交表中的最小功率(方案1)提高1倍,比正交表中的最大功率(方案15)仍提高1.62%。这表明经过优化后得到的制动盘通道方案能够有效提高制动盘的散热能力。
[1] 赵凯辉. 汽车制动器热衰退性能及相关制动安全检测研究[D]. 西安:长安大学, 2010.
[2] MCPHEE A, JOHNSON D. Experimental heat transfer and flow analysis of a vented brake rotor[J]. International Journal of Thermal Sciences, 2008(47):458-467.
[3] MUNISAMY K M, YUSOFF M Z, SHUAIB N H, et al. CFD approach to investigate the flow characteristics in bi-directional ventilated disc brake[C]. AIP Conference Proceedings, 2010.
[4] 潘利科,韩建民,李志强,等. 列车制动盘通风散热的数值仿真[J]. 北京交通大学学报,2015, 39(1): 118-124.
[5] MUNISAMY K M, MOKHTAR H, HASINI H, et al. Investigations on the effect of blade angle on ventilated brake disc using CFD[C]. Orlando, Florida, USA: ASME 2005 International Mechanical Engineering Congress and Exposition, 2005:61-66.
[6] GALINDO LOPEZ C H, TIROVIC M. Understanding and improving the convective cooling of brake discs with radial vanes[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2008, 222(7):1211-1229.
[7] 芦克龙. 基于CFD的汽车制动盘散热性数值计算与优化[D]. 长沙:湖南大学, 2011.
[8] 吴佳伟, 杨志刚. 气流方向对通风制动盘散热性能的影响[J]. 汽车工程学报, 2014, 4(6): 418-423.
[9] 任晓景, 马力, 梁文英. 通风道制动盘的优化设计[J]. 现代零部件, 2012(12):76-78.
[10] SAKAMOTO H. Heat convection and design of brake discs[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2004, 218(3):203-212.
[11] PARK S B, LEE K S, LEE D H. An investigation of local heat transfer characteristics in a ventilated disc brake with helically fluted surfaces[J]. Journal of Mechanical Science and Technology, 2007(21):2178-2187.
[12] PARISH D, MACMANUS D G. Aerodynamic investigations of ventilated brake discs[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2005, 219(4): 471-486.
[13] WALLIS L, LEONARDI E, MILTON B, et al. Air flow and heat transfer in ventilated disc brake rotors with diamond and tear-drop pillars[J]. Numerical Heat Transfer, 2002, 41(6-7):643-655.
[14] AXON Lee, GARRY Kevin, HOWELL J. An evaluation of CFD for modeling the flow around stationary and rotating isolated wheels[C]. SAE Paper 980032.
[15] 单伟, 张苏梅. 应用数理统计[M]. 北京:科学出版社, 2013.
Structural Optimization of Ventilation Channels in Brake Disc Based on Nonlinear Regression
Zheng Weiqi1, Kang Ning1, Liu Xiandong1& Hu Lizhong2
1.SchoolofTransportationScienceandEngineering,BeihangUniversity,Beijing100191;2.DongfengMotorCorporationTechnicalCenter,Wuhan430058
In order to enhance the heat dissipation capability of ventilated brake disc, its internal channel structure is optimized. 16 schemes of ventilation channel are proposed according to the orthogonal design of experiments, the heat dissipation power of inner wall is calculated by using CFD technique, and the significance levels of the factors affecting the heat dissipation of ventilated disc are determined with variance analysis. Then with insignificant factors ignored and the number, the inlet angle and the rib section features of channel taken as arguments, a calculation model for the heat dissipation power of inner wall in brake disk is set up based on nonlinear regression method. Finally genetic algorithm is adopted to find the optimum solutions of ventilation channel: 80 channels with an angle of 20° for both inlet and outlet and No.4 rib. The results of CFD analysis show that the heat dissipation power of inner wall of optimal ventilation channel is 10.465kW, which is 2 times as high as the lowest value among schemes in orthogonal table and is 1.62% higher than the highest value in table, meaning that the optimized ventilation channel structure can effectively improve the heat dissipation capacity of brake disc.
ventilated brake disc; convective heat dissipation; optimization; orthogonal design of experiment; nonlinear regression
*国家自然科学基金(51405011)和北京市自然科学基金(3142013)资助。
原稿收到日期为2015年8月17日,修改稿收到日期为2015年11月19日。

