环间错台效应下基坑开挖引起临近地铁盾构隧道变形的能量计算法

周顺华，何　超，肖军华

(1.同济大学 道路与交通工程教育部重点实验室，上海　201804；2.同济大学 交通运输工程学院，上海　201804)

随着地铁规模的不断扩大，临近运营地铁隧道的基坑工程日益增多，以2014年9月对杭州地铁1号线保护区内的施工活动巡查为例，沿线施工的基坑数量多达19个[1]。基坑开挖会直接引发临近运营地铁盾构隧道的不均匀变形，由此恶化轮轨动力相互作用关系，加速隧道结构性能损伤甚至失效，如盾构隧道管片破坏、结构渗漏水、轨下支承块及道床破裂、钢轨断裂等，对地铁运营安全造成严重威胁。为此上海市地铁沿线建筑施工保护地铁技术管理暂行规定[2]：地铁结构最终绝对位移不能超过20 mm。故研究基坑开挖对临近运营地铁隧道的影响具有重要的实用价值。

针对此类工程问题，国内外一些学者已进行了相关研究[3-16]。文献[3，4]结合工程实测数据，分析了暗挖车站及盾构隧道施工引起的临近既有地铁隧道变形规律；文献[5，6]利用实测数据，推导了基坑开挖卸荷引起临近隧道竖向位移的经验计算公式；文献[7—14]结合具体工程案例，采用有限单元法对周边施工活动引起的临近隧道变形进行数值模拟，将土体和隧道作为一个整体，模拟土体的弹塑性和土—隧道间复杂的相互作用特性；文献[15，16]利用Mindlin解并结合弹性地基梁理论，推导了求解基坑和隧道开挖引起临近地铁隧道变形的弹性地基梁法。综上所述，目前的研究方法可分为经验公式法、有限单元法、弹性地基梁法。经验公式需依靠大量实测数据，使用范围受数据来源限制；有限单元法计算的准确性在很大程度上取决于土体本构模型及参数的选取，且计算量大、建模复杂，需要专业软件；弹性地基梁法属于解析方法，通常采用差分法求解四阶挠曲微分控制方程，计算过程复杂，需较多的分段数才能达到较好的计算精度，不适宜工程应用。

SHEN W. Y.等[17-19]基于最小势能原理，提出分析桩顶承受荷载作用时群桩变形和内力的能量变分法，刘晓强等[20]将其应用于分析隧道开挖引起的管线响应。相比有限单元法和弹性地基梁法，该方法具有积分求解简便、无需对隧道结构进行离散化处理、且容易达到理想的计算精度等优点，便于实际工程中推广应用。

然而无论弹性地基梁法还是能量变分法，均将隧道或管线视为等效均质弹性地基梁，并假设其沿纵向发生弯曲变形。这种假设对于管线有其合理性，然而盾构隧道在纵向上是由一系列衬砌环通过环间螺栓连接而成的多段式拼装结构体系，其可能的纵向变形模式有隧道顶、底部刚性张开和环间错台，王如路[21]结合工程实例分析得出盾构隧道纵向变形模式为环间错台方式，Shui-Long Shen[22]根据上海沉降数据分析也得出相同结论，因此将隧道视为等效均质弹性地基梁的解法显然与实际情况不符。

本文针对现有研究方法的不足，提出环间错台效应下基坑开挖引起盾构隧道变形的能量计算法。利用Mindlin基本解计算基坑开挖卸载引起的盾构隧道附加应力，并通过坐标变换，使得隧道附加应力计算能够考虑基坑与隧道斜交的情况；然后将盾构隧道衬砌环视为由剪切弹簧连接的弹性地基短梁，建立隧道变形计算模型，利用最小势能原理建立变分控制方程并求解，获得环间错台效应下基坑开挖引起临近盾构隧道的竖向、水平位移和环间错台量。将计算结果与弹性地基梁法和现场实测数据对比，以验证本文方法的正确性。

1　基坑开挖引起的隧道附加应力

首先作如下假定：①土体为各向同性的半无限弹性体；②基坑开挖会导致基坑底面和侧壁的卸载，坑底的应力释放率取100%，而侧壁的释放应力全部由支撑体系平衡，不作考虑；③不考虑隧道存在对土体附加应力计算的影响。

定义参数：L，B和h分别为基坑开挖的长度、宽度和深度；Z0为隧道轴线的埋深；L0为隧道轴线距离基坑中心的水平距离；D为隧道外径；γ为土体重度；μ为泊松比；Ω为基坑开挖区域。

当基坑与临近盾构隧道平行时，两者的位置关系如图1所示。

图1　基坑与临近隧道位置关系

基于上述假定，基坑开挖的力学效应，理论上可认为是在基坑底部施加竖直向上的均布荷载。以地表处基坑中心为原点建立三维直角坐标系x′y′z′，根据Mindlin基本解[23]可知，在基坑底部某点(ξ,η,h)的荷载(γhdξdη)作用下，引起隧道轴线上点(x′,L0,Z0)的竖向附加应力σz和水平附加应力σy分别为

(1)

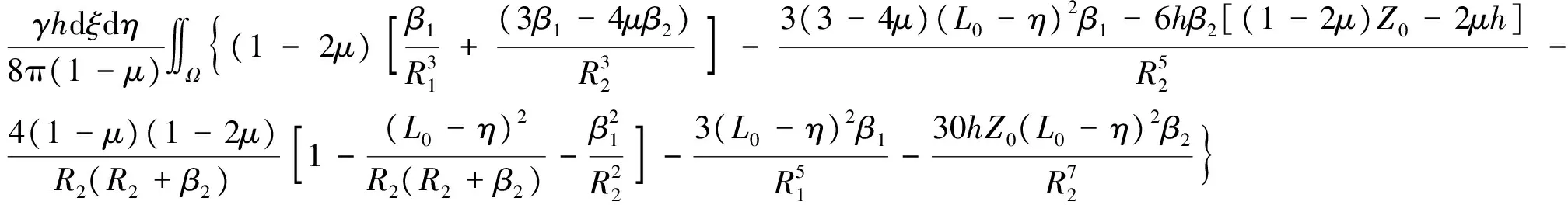
(2)

其中，

β1=Z0-h

β2=Z0+h

针对基坑与隧道斜交的情况，则可在两者平行的基础上通过坐标变换进行考虑。如图2所示，隧道轴线上距离基坑中心最近点为(x0′,y0′,z0′)，以该点在平面上的投影点(x0′,y0′, 0)为原点，隧道轴线方向为x轴，与隧道轴线垂直方向为y轴，竖直方向为z轴建立新坐标系xyz。因此隧道轴线上的点在新坐标系xyz中的坐标(x,y,z)可分别按下式由原坐标(x′,y′,z′)得到，即

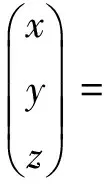
(3)

式中：θ为斜交夹角，顺时针为正，逆时针为负。

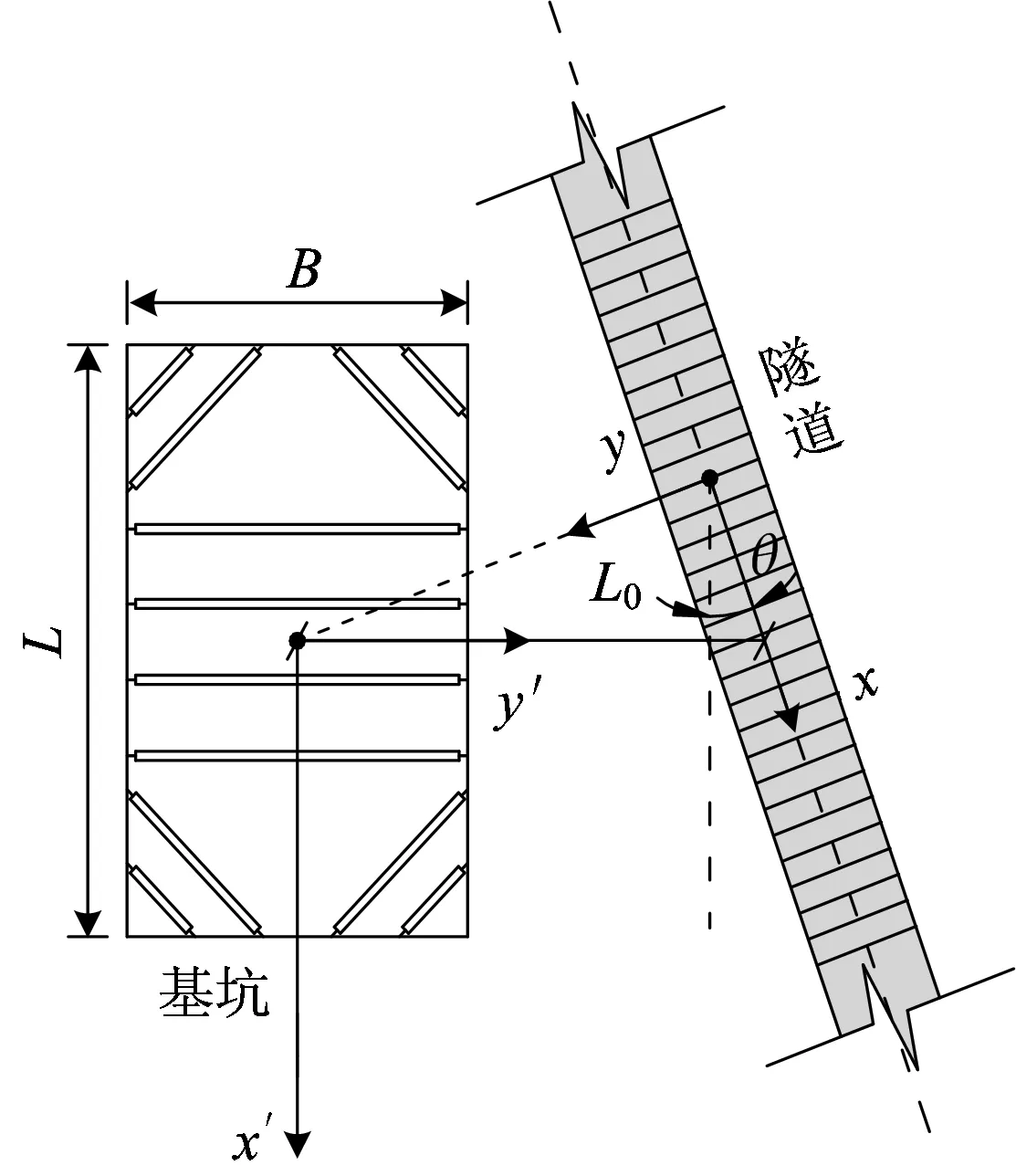
图2　基坑与隧道斜交时计算模型平面投影图

2　考虑环间错台效应的隧道纵向变形计算

2.1　基坑开挖引起临近盾构隧道的总势能

将盾构隧道视为一系列由剪切弹簧连接的弹性地基短梁，基坑开挖会导致盾构隧道发生错台变形，由此建立的隧道纵向变形计算模型如图3所示。任取1环宽为δ编号为m的衬砌环，其所受荷载Fl由3部分组成。①基坑开挖引起的土体附加荷载；②地基抗力；③环间剪切力。Fl可表示为

Fl=Pl(x)-kDsl(x)-kt[wl((m+1)δ)-wl(mδ)]-kt[wl(mδ)-wl((m-1)δ)]

(4)

其中，Pl(x)=Dσl

式中：Pl(x)为隧道受到的土体附加荷载；σl为基坑开挖引起的隧道附加应力， 由式(1)和式(2)确定；l为坐标方向，l=2, 3分别对应于y和z坐标方向，即隧道的水平方向和竖向；sl(x)为地基弹簧的位移， 根据位移协调条件可知sl(x)=wl(x)， 而wl(x)为盾构隧道位移；kt为环间剪切刚度；k为地基基床系数，采用Vesic[24]公式计算；Es为地基土弹性模量；Et为盾构隧道衬砌环的弹性模量；It为惯性矩。

图3　考虑环间错台效应的隧道纵向变形计算模型

根据隧道每环管片受力情况，可得基坑开挖引起的临近盾构隧道总势能也由以下3部分组成。

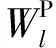
(5)

式中：2N为受基坑开挖影响的隧道衬砌环数。

(6)

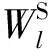
(7)

综合式(5)—式(7)可得基坑开挖引起的临近盾构隧道总势能为

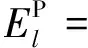
(8)

2.2　盾构隧道位移的级数展开

在基坑与隧道斜交情况下，盾构隧道位移并非左右对称，故将其展开为傅里叶级数时包含正弦和余弦2部分，即

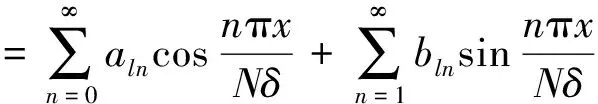
=(Tcn(x)Tsn(x))(AlBl)T

(9)

其中，

Al=(al0al1…aln)T

Bl=(bl1bl2…bln)T

式中：Al和Bl为傅里叶级数中的待求系数矩阵；n为傅里叶级数的展开阶数。

2.3　变分控制方程及其求解

将隧道位移展开式(9)带入式(8)，基于最小势能原理，对隧道总势能取极值，即

(10)

对式(10)求解，整理得环间错台效应下基坑开挖对临近盾构隧道影响的变分控制方程为

1)δ)Tsn((m+1)δ))-(Tcn(mδ)Tsn(mδ))]+

(11)

将式(11)化简并写成矩阵形式可得

(Kt+Ks)(AlBl)T=(PlcnPlsn)T

(12)

其中，

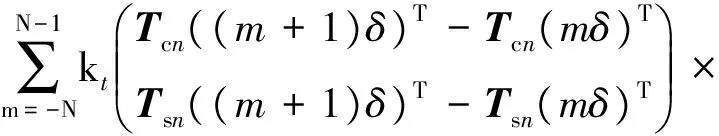
(Tcn((m+1)δ)-Tcn(mδ)Tsn((m+1)δ)-Tsn(mδ))

式中：Kt为隧道环间剪切刚度矩阵；Ks为土体刚度矩阵。

由式(12)可求得系数矩阵Al和Bl，将其代入式(9)便可求得基坑开挖引起临近盾构隧道的竖向位移和水平向位移。

任意相邻衬砌环间错台量Δwl的计算公式为

Δwl=wl(mδ)-wl((m-1)δ)

(13)

3　算例分析

选取2个临近隧道的基坑工程实例，工程概况见表1。

表1　临近盾构隧道的基坑工程实例

3.1　工程实例1

采用本文方法计算得到工程实例1中上、下行线盾构隧道的竖向位移，如图4所示；为了验证本文方法的正确性，将弹性地基梁法的计算结果[15]以及实测数据[10]也绘于图4中。由图4可知：本文方法计算得到的与实测的盾构隧道竖向位移变化规律基本一致，均呈明显的高斯正态分布；相对于弹性地基梁法，本文方法所得的隧道变形槽宽度更小，并且与实测结果更为接近；本文方法计算所得上、下行线隧道最大竖向位移与实测数据的偏差量分别为2.1和4.9 mm，能够满足实际工程预测需要。此外，由于本文方法无需对隧道进行离散化处理，具有更高的计算效率。由此说明本文方法可应用于实际工程中估算基坑开挖引起盾构隧道的竖向位移。

采用本文方法并按照考虑和不考虑基坑与隧道斜交2种情况计算隧道的竖向位移，如图5所示。由图5(a)可知：对于上行线隧道(位于基坑正下方)，无论是否考虑基坑与隧道斜交，所得的隧道竖向位移曲线基本一致，最大竖向位移仅相差0.3 mm，说明当隧道位于基坑正下方时，斜交角度对隧道纵向位移影响很小，可忽略不计。由图5(b)可知：对于下行线隧道(距离基坑中心线18 m)，考虑基坑与隧道斜交与否，所得的盾构隧道竖向位移相差较大；考虑斜交时所得的盾构隧道竖向位移与实测的更加吻合；不考虑斜交时所得的盾构隧道最大竖向位移仅为2.4 mm，远小于实测的11.9 mm；说明当隧道不位于基坑正下方，特别是从基坑侧旁穿行时，须考虑斜交角度对计算结果的影响，这主要是因为当隧道位于基坑旁侧时，斜交角度的不同会导致隧道至开挖区域间的距离差别较大，使得隧道受基坑开挖影响引起的附加荷载差异较大，进而导致隧道的变形差异也较大；而当隧道位于基坑正下方时，则不存在此现象。

图4　工程实例1隧道竖向位移对比

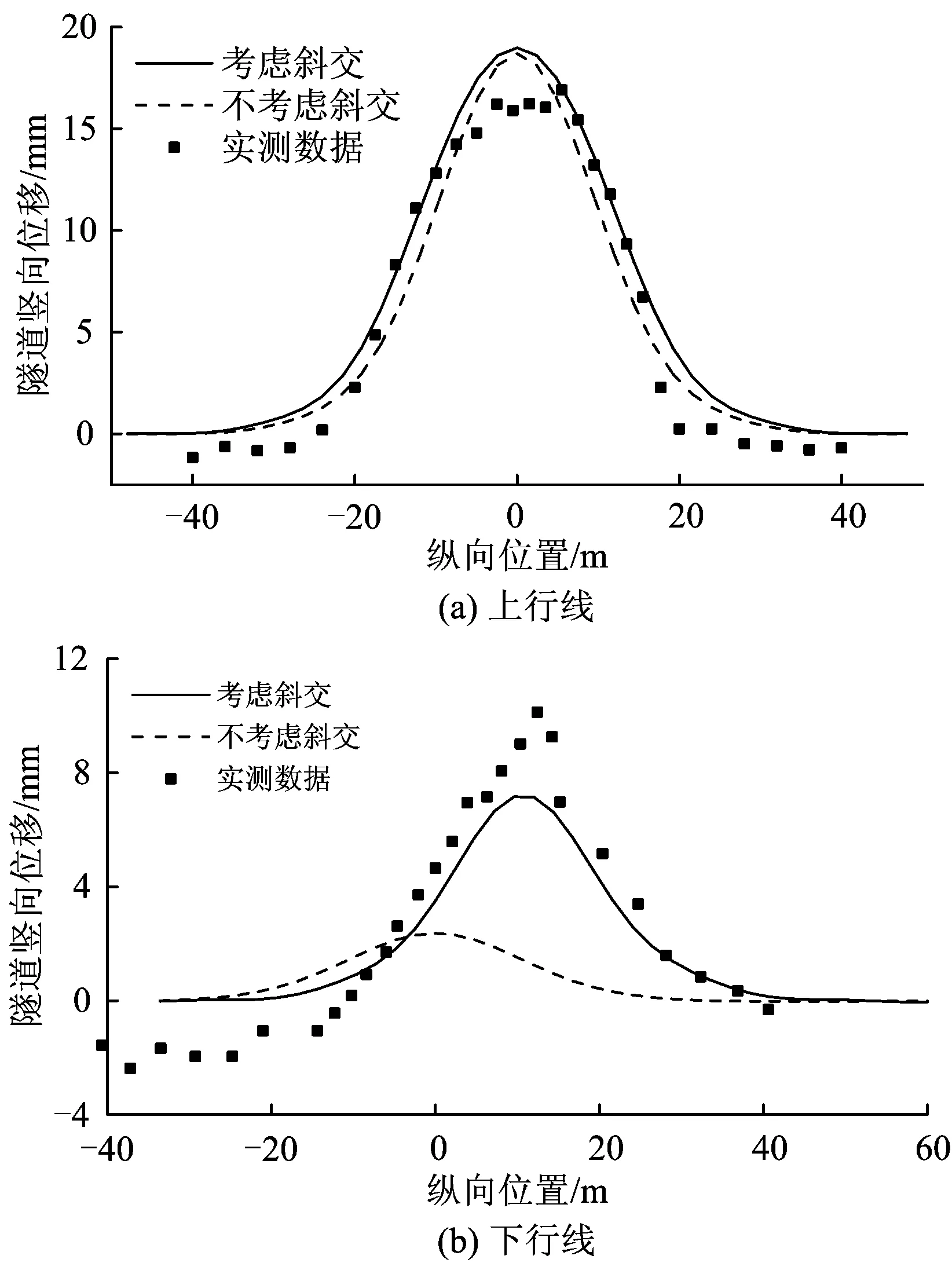
图5　考虑基坑与隧道斜交与否对隧道竖向位移的影响

隧道环间错台是影响盾构隧道结构安全的重要因素之一，过大的错台量会引发管片局部开裂、接缝渗漏、甚至凹凸榫碎裂等病害，从而严重影响结构和行车的安全，因此对基坑开挖引起的隧道环间错台量进行估算十分必要。

对于工程实例1，采用本文方法计算得到的隧道环间错台分布如图6所示。由图6可知：在竖向位移最大值位置上基本不发生环间错台；随着位移减小，环间错台量逐渐增大，直到位移高斯曲线的反弯点上，环间错台量达到最大，随后错台量逐渐减小；较大的错台量主要集中在竖向位移曲线反弯点两侧一定范围内，即隧道差异变形较大的区域。工程实例1中基坑开挖引起上、下行隧道环间最大错台量分别为1.3和0.6 mm，可见，即便基坑开挖引起的环间错台量较小，但在基坑开挖影响范围内隧道竖向变形仍然可以累积到较大的量值。

图6　工程实例1隧道环间错台分布

3.2　工程实例2

对于工程实例2，采用本文方法计算所得下行线盾构隧道的竖向位移和水平位移如图7所示，并与实测数据[13]对比分析。由图7可知：计算所得下行线盾构隧道的竖向位移和水平位移与实测结果基本一致，计算所得的最大竖向位移、水平位移分别为3.6和5.3 mm，相比实测值，分别仅相差0.3和1.6 mm，说明本文方法可同时应用于实际工程中估算基坑开挖引起隧道的竖向位移和水平位移。

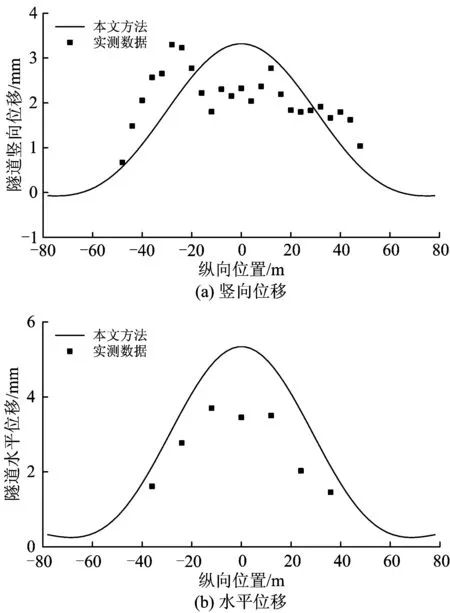
图7　工程实例2隧道竖向和水平位移曲线对比

4　结　论

(1)将隧道视为由剪切弹簧连接的弹性地基短梁，提出环间错台效应下基坑开挖引起临近盾构隧道变形的能量计算法。首先采用Mindlin基本解计算基坑开挖卸载引起的隧道附加应力，并通过坐标变换使其可以考虑隧道与基坑轴线存在夹角的情况；然后将盾构隧道衬砌视为由剪切弹簧连接的弹性地基短梁，建立隧道变形计算模型，利用最小势能原理建立变分控制方程并求解，从而获得环间错台效应下基坑开挖引起临近盾构隧道的竖向位移、水平位移和环间错台量。将计算结果与弹性地基梁法和现场实测数据对比可知，本文方法与实际情况吻合更好，且本文方法无需对隧道进行离散化处理，具有更高的计算效率，可用于实际工程中预测基坑开挖引起临近盾构隧道的竖向位移、水平位移和环间错台量。

(2)当盾构隧道位于基坑正下方时，无论考虑斜交角度与否，所得结果基本一致；而当盾构隧道位于基坑旁侧时，斜交角度对计算结果的影响很大，考虑斜交角度的计算结果更加符合实际情况。

(3)基坑开挖引起的盾构隧道最大环间错台量所在位置并非位于最大位移点处，而是在位移高斯曲线的反弯点上，即盾构隧道差异变形最大处；且即便基坑开挖引起的环间错台量较小，但在基坑开挖影响范围内盾构隧道的竖向变形仍然可以累积到较大的量值。

[1]杭州杭港地铁有限公司.杭州地铁1号线地铁保护区巡查月度报告[R]. 杭州: 杭州杭港地铁有限公司, 2014.

[2]上海市市政工程管理局. 上海市政法(94)第854号 上海市地铁沿线建筑施工保护地铁技术管理暂行规定[S]. 上海: 上海市市政工程管理局, 1994.

[3]张成平, 张顶立, 吴介普, 等. 暗挖地铁车站下穿既有地铁隧道施工控制[J]. 中国铁道科学, 2009,30(1): 69-73.

(ZHANG Chengping, ZHANG Dingli, WU Jiepu, et al. Construction Control of a Newly-Built Subway Station Undercrossing the Existing Subway Tunnel[J]. China Railway Science, 2009,30 (1): 69-73.in Chinese)

[4]孙玉永, 周顺华, 向科, 等. 近距离下穿既有隧道的盾构施工参数研究[J]. 中国铁道科学, 2010, 31(1): 54-58.

(SUN Yuyong, ZHOU Shunhua, XIANG Ke, et al. Study on the Construction Parameters of Shield Tunneling in Short-Distance Undercrossing the Existing Tunnel[J]. China Railway Science, 2010, 31(1): 54-58.in Chinese)

[5]李志高, 刘浩, 刘国彬, 等. 基坑开挖引起下卧隧道位移的实测分析[J]. 地下空间与工程学报, 2005,1(4): 619-623.

(LI Zhigao, LIU Hao, LIU Guobin, et al. Influence Analysis of Deep-Dip Excavation on Down Tunnel Based on the Measured Displacement[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(4): 619-623.in Chinese)

[6]魏纲. 基坑开挖对下方既有盾构隧道影响的实测与分析[J]. 岩土力学, 2013, 34(5): 1421-1428.

(WEI Gang. Measurement and Analysis of Impact of Foundation Pit Excavation on Below Existed Shield Tunnels[J]. Rock and Soil Mechanics, 2013, 34(5): 1421-1428.in Chinese)

[7]DOLEZALOVA M. Tunnel Complex Unloaded by a Deep Excavation[J]. Computers and Geotechnics, 2001, 28(6/7): 469-493.

[8]HU Z F, YUE Z Q, ZHOU J, et al. Design and Construction of a Deep Excavation in Soft Soils Adjacent to the Shanghai Metro Tunnels[J]. Canadian Geotechnical Journal, 2003, 40(5): 933-948.

[9]房倩, 张顶立. 浅埋暗挖地铁车站下穿既有线结构施工方法研究[J]. 中国铁道科学, 2007, 28(5): 71-77.

(FANG Qian, ZHANG Dingli. Study on the Shallow Tunnel Construction Methods for a New-Built Subway Station Passing Through the Bottom of the Existing Subway[J]. China Railway Science, 2007, 28(5): 71-77.in Chinese)

[10]徐凌, 黄宏伟. 基坑开挖对下卧地铁隧道的影响研究[J]. 岩土工程学报, 2008, 30(增刊): 164-166.

(XU Ling, HUANG Hongwei. Effect of Foundation Pit Excavation on Underlying Metro Tunnels[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(Supplement):164-166.in Chinese)

[11]张玉成, 杨光华, 姚捷, 等. 基坑开挖卸荷对下方既有地铁隧道影响的数值仿真分析 [J]. 岩土工程学报, 2010,32(增刊1): 109-115.

(ZHANG Yucheng, YANG Guanghua, YAO Jie, et al. Numerical Simulation and Analysis of Effect of Excavation of Foundation Pits on Metro Tunnels[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(Supplement 1): 109-115.in Chinese)

[12]陈孟乔, 杨广武. 新建地铁车站近距离穿越既有地铁隧道的变形控制[J]. 中国铁道科学, 2011,32(4): 53-59.

(CHEN Mengqiao, YANG Guagwu. Deformation Control of a Newly-Built Subway Station Crossing the Adjacent Existing Subway Tunnel[J]. China Railway Science, 2011, 32(4): 53-59.in Chinese)

[13]邵华, 王蓉. 基坑开挖施工对邻近地铁影响的实测分析[J].地下空间与工程学报, 2011, 7(增刊1):1403-1408.

(SHAO Hua, WANG Rong. Monitoring Data Analysis on Influence of Operating Metro Tunnel by Nearly Excavation Construction[J]. Chinese Journal of Underground Space and Engineering, 2011, 7 (Supplement 1):1403-1408.in Chinese)

[14]黄宏伟, 黄栩, SCHWEIGER F Helmut. 基坑开挖对下卧运营盾构隧道影响的数值模拟研究[J]. 土木工程学报,2012, 45(3): 182-189.

(HUANG Hongwei, HUANG Xu, SCHWEIGER F Helmut. Numerical Analysis of the Influence of Deep Excavation on Underneath Existing Road Tunnel[J]. China Civil Engineering Journal, 2012, 45(3): 182-189.in Chinese)

[15]张治国, 黄茂松, 王卫东. 邻近开挖对既有软土隧道的影响[J]. 岩土力学, 2009, 30(5): 1373-1380.

(ZHANG Zhiguo, HUANG Maosong, WANG Weidong. Responses of Existing Tunnels Induced by Adjacent Excavation in Soft Soils[J]. Rock and Soil Mechanics, 2009, 30(5): 1373-1380.in Chinese)

[16]许有俊, 陶连金, 文中坤, 等. 新建地铁隧道上穿既有隧道引起的结构隆起变形[J]. 中国铁道科学, 2014, 35(6): 48-54.

(XU Youjun, TAO Lianjin, WEN Zhongkun, et al. Upheaval Deformation Induced by Newly-Built Metro Tunnel Upcrossing Existing Tunnel[J]. China Railway Science, 2014, 35(6): 48-54. in Chinese)

[17]SHEN W Y，Chow Y K，Yong K Y. Variational Approach for Vertical Loaded Pile Groups in an Elastic Half Space [J]. Geotechnique,1999, 49(2): 199-213.

[18]SHEN W Y，Chow Y K，Yong K Y. A Variational Approach for the Analysis of Pile Group-Pile Cap Interaction [J]. Geotechnique, 2000, 50(4): 349-357.

[19]SHEN W Y, TEH C I. Analysis of Laterally Loaded Pile Groups Using a Variational Approach [J]. Geotechnique,2002, 52(3): 201-208.

[20]刘晓强, 梁发云, 张浩,等. 隧道穿越引起地下管线竖向位移的能量变分分析方法[J]. 岩土力学, 2014, 35(增刊2): 217-222，231.

(LIU Xiaoqiang, LIANG Fayun, ZHANG Hao, et al. Energy Variational Solution for Settlement of Buried Pipeline Induced by Tunneling[J]. Rock and Soil Mechanics, 2014, 35(Supplement 2): 217-222，231.in Chinese)

[21]王如路. 上海地铁盾构隧道纵向变形分析[J]. 地下工程与隧道, 2009 (4):1-6.

(WANG Rulu. Analysis on the Longitudinal Deformation of Shield Tunnel of Shanghai Metro[J]. Underground Engineering and Tunnels, 2009 (4): 1-6.in Chinese)

[22]SHEN Shuilong, WU Huaina, CUI Yujun, et al. Long-Term Settlement Behaviour of Metro Tunnels in the Soft Deposits of Shanghai[J]. Tunnelling and Underground Space Technology, 2014, 40:309-323.

[23]MINDLIN R D. Forces at a Point in the Interior of a Semiinfinite Solid[J]. Journal of Applied Physics, 1936, 7(5): 195-202.

[24]VESIC A B. Bending of Beams Resting on Isotropic Elastic Solids[J]. Journal of Engineering Mechanics, 1961, 87(2): 35-53.

[25]闫治国, 彭益成, 丁文其, 等. 青草沙水源地原水工程输水隧道单层衬砌管片接头荷载试验研究[J]. 岩土工程学报, 2011, 33(9): 1385-1390.

(YAN Zhiguo, PENG Yicheng, DING Wenqi, et al. Load Tests on Segment Joints of Single Lining Structure of Shield Tunnel in Qingcaosha Water Conveyance Project[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1385-1390.in Chinese)

[26]朱伟, 黄正荣, 梁精华. 盾构衬砌管片的壳-弹簧设计模型研究[J]. 岩土工程学报, 2006, 28(8): 940-947.

(ZHU Wei, HUANG Zhengrong, LIANG Jinghua. Studies on Shell-Spring Design Model for Segment of Shield Tunnels[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(8): 940-947.in Chinese)