运动控制系统速度平滑技术研究与实现

摘 要：插补算法和速度控制是运动控制系统的核心，控制系统除了对插补算法有一定要求，对执行机构速度控制的精准度要求也非常高。为了提高执行机构的效率和精度，本文研究了速度控制中的T型曲线控制、S型曲线控制模型，并最终在软件上实现，从而提高了运动控制系统的精准度。

关键词：插补算法；平滑处理；速度控制

DOI：10.16640/j.cnki.37-1222/t.2016.07.240

1 引言

插补算法是实现被控设备精确运行的基础，他的作用是依据相关数据通过一定方法求出各个轴的分量，最终实现精确的运动轨迹。所以运动控制系统中，插补算法对系统系能起着非常关键的作用。或者说插补技术是，已知运行曲线的一些数据，通过一定的计算方法让数据点密化。插补方法常见的有直线插补法、圆弧插补法，其他复杂的插补算法都是以它为基础。

运动控制系统中，速度平滑技术的优劣也会对插补算法的效果产生影响。运动控制系统插补过程中的速度平滑技术，本质就是执行电机的加减速控制技术。在控制系统的插补过程中，速度控制技术非常重要，电机能否快速启停、能否迅速达到预设速度、速度调整算法的效率都会影响到插补执行的精准度[1]。

常见的算法模型有直线控制算法、指数控制算法。另外还可以利用三角函数构造出控制曲线，这种控制方法使得速度、加速度以及位移均连续，减弱了对机床的柔性冲击。尽管三角函数加减控制法可以实现更加平滑，但因为计算复杂，在控制前须对数据进行处理、将算法数据存放在内存中通过查表实现。三角函数控制算法的缺点是插补周期长，加工速度慢。本文研究了T型算法控制、S型算法控制及其实现方法[2]。

2 T型算法分析

T型加减速算法的数学模型表达式为： V（t）=V（0）+A*T （1）

T型算法主要分为三个阶段：第一阶段是均匀加速阶段。V0是初始的运行速度，Vm是最大的运行速度。但是，有时因为目标的位移量太短，不一定非得有匀速阶段，所以在第一阶段应根据已经走的位移量、目标位移量计算是否有匀速阶段；第二阶段是匀速阶段。加速度大小为零，保持最大速度匀速运动。在第二阶段中应根据走过的位移量、目标位移量计算匀速的步数、并预测何时减速，并在最后进入减速的阶段；第三阶段是均匀减速阶段。其运动过程和第一阶段完全相反，期间将依据走过的减速步数和计算的减速步数比较从而决定是否退出。

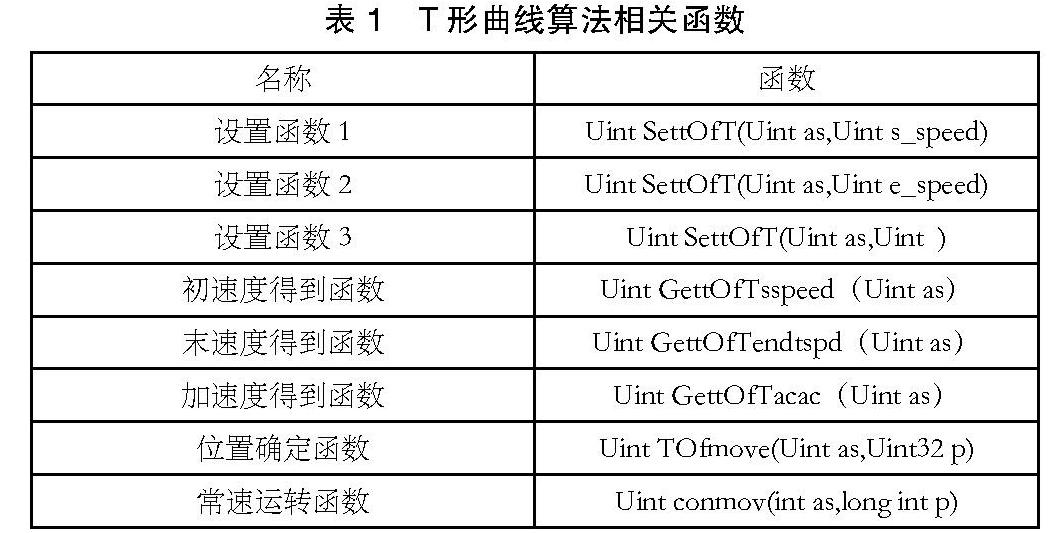
程序设计相关函数和数据结构设计如表1：

3 S型算法分析

因为T型曲线算法的加速度不是连续的，加减速在执行机构启动、结束时因加速度的突变会产生一定冲击，所以不适合于高精度的数控系统。而采用S型加减速算法可以解决冲击问题。

S算法曲线的加减速过程一共分为七阶段：加加速阶段、匀加速阶段、减减速阶段、匀速阶段、减减速阶段、匀减速阶段、加减速阶段。为了方便算法数据的处理，可以让S曲线对称。

第一阶段：加加速的阶段，最高的速度是V1，加加速度大小是J，加速度大小从0匀加速上升到Am。

第二阶段：匀加速的阶段，最低速度大小是V1、最高速度大小是V2，加速度大小是Am。

第三阶段：减加速的阶段，加加速度大小是-J、最低速度大小是V2、最高速度大小是Vmax， 加速度大小是从Am匀减速直到0。

第四阶段：匀速的阶段，以最大速度Vmax匀速运行。第五、六、七阶段与一、二、三阶段是相反对称的过程，这里不加以描述。

从上面的分析知道，加速度没有突变现象，是均匀在变化的，所以采用S型加减速算法能够消除对执行电机的冲击。位移是速度积分的结果，速度是加速度积分的结果，加速度是加加速度积分的结果，所以最终能够推导出S型曲线算法的加速度、速度计算公式。

S加减速算法缺点是由于加加速度不连续因而柔性不太好，加减速过程通过分段连续实现更加复杂。而采用数学构造法产生的曲线进行改进，能够使系统柔性更好的同时还能够用数学公式表示，而且程序容易实现。

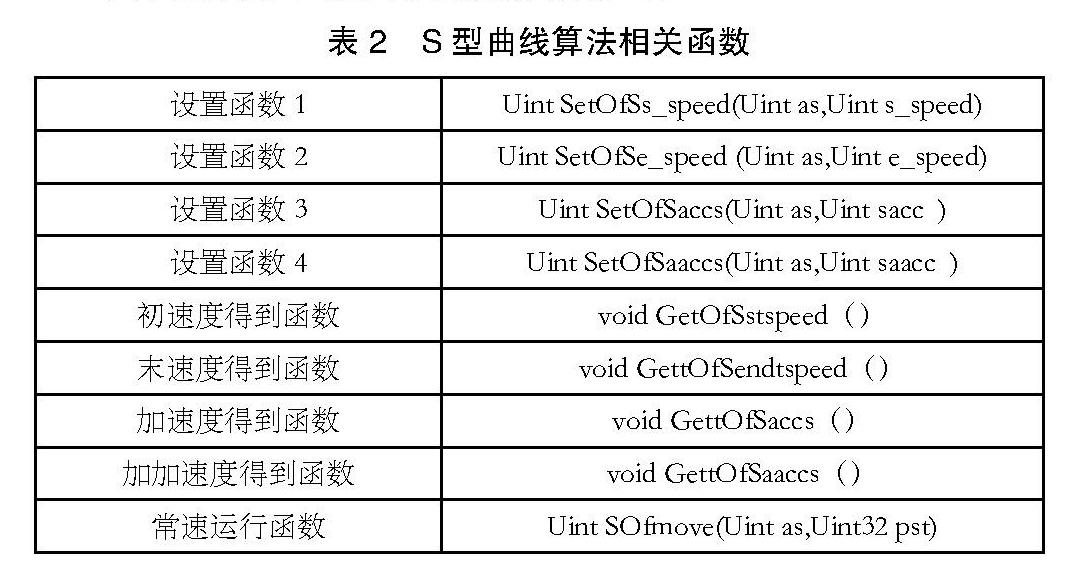
程序设计相关函数列表和数据结构如表2：

4 总结

控制系统除了对插补算法有一定要求，对执行机构速度控制的精准度要求也非常高。为了提高执行机构的效率和精度，本文研究了速度控制中的T型曲线控制、S型曲线控制模型，并最终在软件上实现，从而提高了运动控制系统的精准度。T型曲线是实际运用中最普遍的方法，存在加减速突变，适合于低端系统。 采用S型算法实现较难，但是可以减少电机的启动冲击，适合于要求较高的系统。S加减速算法缺点是由于加加速度不连续因而柔性不太好，加减速过程通过分段连续实现更加复杂。而采用数学构造法产生的曲线进行改进，能够使系统柔性更好的同时还能够用数学公式表示，而且程序容易实现。

参考文献：

[1]张志强，汪文津，王太勇.基于开放式计算机数控系统的插补软件模块开发[J].机床与液压，2010（20）.

[2]崔铁.数控机床的嵌入式运动控制器的设计[D].东北大学，2009.

作者简介：石平政（1985-），男，湖北阳新人，硕士研究生，助讲，研究方向：机电控制、电路系统。