新型UHPC连续箱梁桥的体外预应力锚固构造形式研究

邵旭东　张良　张松涛　欧阳泽卉

摘 要：针对新型UHPC连续箱梁桥的结构特点及预应力体系布置，对其腹板处体外预应力下折索进行齿块锚固研究.对独立矩形齿块进行应力分析，揭示板厚对锚固区壁板外侧 “局部弯曲效应”的影响.通过拓扑优化分析构建出一个揭示齿块锚固区传力机理的简化平面杆系模型，提出两种齿块锚固区局部加强的方法.在此基础上，对UHPC箱梁桥的腹板体外预应力锚固齿块进行构造设计，对比6种不同锚固方案，分析横隔板、预应力筋齿块内转向和锚固长度对锚固区受力的影响，最终得出较为合理的体外预应力齿块锚固构造形式.

关键词：桥梁工程；构造形式；有限元分析；体外预应力锚固齿块；超高性能混凝土；薄壁箱梁

中图分类号：U448.21 文献标识码：A

文章编号：1674-2974（2016）03-0001-07

超高性能混凝土（Ultra High Performance Concrete， UHPC）具有高弹性模量、高抗压强度、高抗拉强度和良好的徐变特性等优点[1-5]，已在工程实践中获得应用.作者团队提出一种超大跨径单向预应力连续箱梁桥新体系，即将超高性能混凝土、密集横隔板薄壁箱梁与部分体外预应力进行有机结合的结构，研究了400 m级连续箱梁桥结构的概念设计[6].由于箱梁板件较薄，该方案采用了部分体外预应力体系以满足受力和施工的要求.同时，由于UHPC具有优异的抗拉性能，在箱梁中设置了密集横隔板，可以取消横向和竖向预应力，将传统三向预应力结构体系转变为纵向单向预应力结构体系，从而降低施工难度，保证预应力施工质量.

传统混凝土梁桥体外预应力钢束主要集中在锚固横梁或厚实的横隔板上，较少锚固在齿块上[7].但UHPC梁桥由于壁厚较薄，在体内和体外混合配索中体外预应力索所占的比率较大，节段施工中有大量的体外预应力束锚固在腹板和顶、底板的齿块上.齿块对结构局部受力要求较高，对具体构造的要求也较复杂，虽然在普通混凝土体外预应力梁桥中已有应用，但由于新型UHPC箱梁结构壁板厚度的减小和结构形式的改变，其具体锚固构造形式有待进一步研究.

本文从构造相对简单的独立矩形齿块入手，通过有限元分析得出齿块锚固区拉应力分布特征，由传力路径的拓扑优化分析构造一个简化的平面杆系模型以揭示锚固区局部抗弯特点，并在此基础上提出两种齿块锚固区局部加强方法，最后针对带密集横隔板的UHPC薄壁箱梁结构提出一种可行的体外预应力齿块锚固形式.

1 独立矩形齿块的应力分布特征

1.1 拉应力的集中分布特征

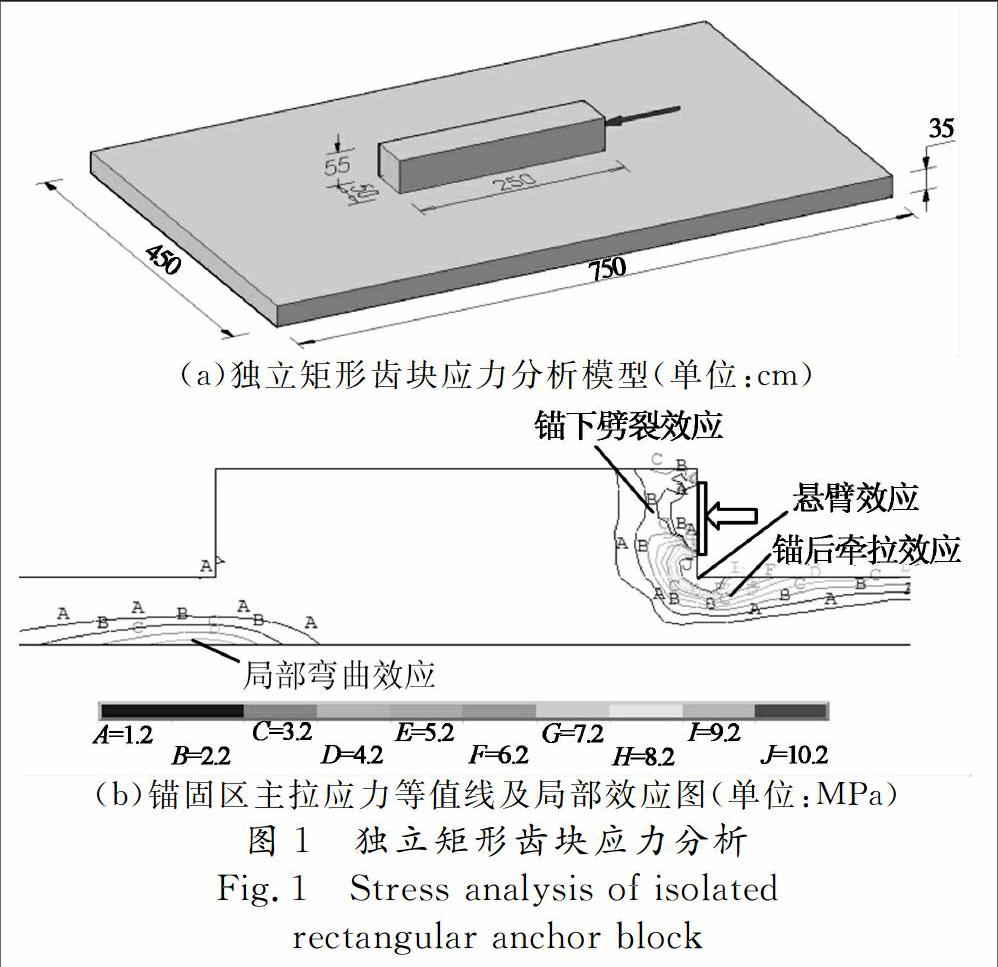
对一简化的独立矩形齿块进行应力分析（见模型示意图1（a）），板厚为35 cm.利用通用有限元软件ANSYS进行弹性计算，采用 Solid95单元模拟锚固区混凝土，UHPC材料参数采用文献[6]中的试验值，弹性模量E取42.6 GPa，泊松比υ取0.2.在计算模型的锚前板端施加固定约束，横向两侧施加竖向约束.锚固集中力按19束预应力筋张拉力计算，荷载取为3 193 kN.锚固力等效为均布荷载施加在垫板范围内的节点上，按照理想弹性材料计算得到齿块锚固区的应力分布，对称截面主拉应力等值线见图1（b）.由拉应力等值线可知，集中力作用下的独立矩形齿块存在明显的拉应力集中现象，主要有4种局部作用效应，分别为：

1） 悬臂效应：齿块锚固面与壁板交界处的横向拉应力集中；

2） 锚后牵拉效应：锚后壁板内侧由纵向拉力与局部弯曲共同作用产生的纵向拉应力集中；

3） 锚下劈裂效应：锚下横向拉应力集中；

4） 局部弯曲效应：锚前处壁板外侧由于局部弯曲产生的拉应力集中.

1.2 壁板厚度对局部弯曲效应的影响

文献[8]中对普通混凝土齿块锚固区的应力分析中忽略了板外侧产生的“局部弯曲效应”，考虑到UHPC箱梁的壁厚减薄，对上述有限元模型采用不同的板厚计算壁板外侧最大主拉应力值，得到如图2所示曲线.

由图2可知，当板厚减小时，外侧最大主拉应力值急剧增加，板厚减小为20 cm时，主拉应力达到18.75 MPa，可见壁板抵抗“局部弯曲效应”的能力与板厚密切相关.当UHPC薄壁箱梁桥板厚减小为20 cm时，若直接采用独立矩形齿块进行体外预应力锚固，将对箱梁结构局部产生较大削弱，有必要采取相应措施减小壁板产生的“局部弯曲效应”.

2 体外预应力齿块锚固区局部加强方法

2.1 锚固区局部抗弯特征

通过拓扑优化分析，可以从连续体结构中剔除传力效率不高的部分，最终得到结构的主要荷载传递构架，能够较为直观地看出结构的传力特点.这里利用通用有限元软件ANSYS的拓扑优化模块对一简化的锚固模型进行连续体结构拓扑优化分析.基于ANSYS的结构拓扑优化采用变密度法[9]，其基本思想为：定义取值范围为[0，1]的相对密度μ，将优化目标用相对密度μ的显性函数表示， 然后运用数学规划法或优化准则法求解.约束函数是在给定载荷和最小柔度情况下缩减结构体积的百分比.目标函数是在满足结构约束的条件下使整体的变形能最小，等效于整体的刚度最大.

简化模型如图3（a）所示，优化约束条件设置为缩减50%的体积，采用OC法（优化准则法）进行拓扑优化，相对密度在0.5～1的部分得以保留.在横向两侧有约束的情况下最优拓扑构形如图3（b）所示，优化后得到的拓扑构形在壁板的底部形成了两道“横肋式结构”.锚固纵向截面的拓扑密度分布及结构内部3个关键位置的拉压力平衡如图3（c）所示.在忽略板的局部抗弯能力情况下，由拓扑构形得到一个简化的平面杆系模型以揭示其偏心受压特点，如图3（d）所示.

2.2 锚固区局部加强的2种方法

由前文独立矩形齿块应力分析发现，薄板的局部抗弯能力较弱，而拓扑优化得到的简化模型（图3（d））忽略了板的局部抗弯能力，因此由公式（1）可知，为了减小偏心弯矩对结构的影响，在锚固力P与偏心距e一定时，可以增加锚固长度L或者提供一个与壁板垂直的力F.增加锚固长度L是较常采用的方法，现从提供与壁板垂直的分力F考虑，本文提出以下2种方法对齿块锚固区局部加强.

1）对于具有隔板的薄壁结构，可以将齿块的前后端布置于隔板位置，由隔板提供垂直于壁板的支承力F，此时横隔板作用类似于图3（b）中的“横肋式结构”.因此UHPC密集横隔板箱梁结构可以考虑利用隔板的支承作用进行齿块锚固.

2）考虑到另一种提供垂直分力的方式是利用预应力筋在锚固块内的转向产生的径向力作用，这与体内索齿块锚固时相似.如图4所示，预应力筋张拉力为P，偏转角度为θ，当不考虑管道摩擦阻力时，径向力大小为：

3 锚固方案构造优化设计

在前文独立矩形齿块分析的基础上，对文献[6]中400 m级UHPC连续箱梁在悬臂施工阶段腹板处的体外预应力齿块锚固进行构造优化设计，减小体外预应力锚固构造对箱梁主体结构的削弱.

3.1 实桥方案简化模型

UHPC箱梁桥整体布置及截面尺寸如图5（a）和5（b）所示，对图5（a）所示的体外预应力布置情况进行锚固构造设计.为方便建模分析，将计算节段变截面简化为等截面梁，薄壁箱梁取梁高12 m，长24 m，壁厚20 cm，每隔4 m布置一道横隔板，隔板厚12 cm，简化的计算节段模型如图5（c）所示.由于体外预应力索偏转角度较小，张拉产生的竖向分力对锚固区的局部受力影响较小，因此在锚固构造局部分析时采用水平布置形式进行计算.锚固齿块位于腹板竖向中间位置时对局部受力最为不利，对其进行锚固构造设计与计算.

3.2 局部承压尺寸设计

为了确定齿块的锚固端面尺寸，进行局部承压计算.现行美国规范AASHTO[10]和ACI318[11]将锚固区分为局部锚固区和总体锚固区，对局部锚固区设计主要解决受压问题，总体锚固区设计则解决的是受拉问题.对于局部锚固区，主要进行局部受压承载力验算，然而现有规范都是针对普通混凝土，对于UHPC并不适用.本文参考文献[12]进行初步的局部承压尺寸设计，文献[12]中通过局部承压试验得出了带钢纤维的活性粉末混凝土（SFR-RPC）的承载力计算公式：

因此，按承载力计算得到的图示尺寸布置满足要求，即在不考虑配置间接钢筋的情况下，UHPC满足局部承压要求.

3.3 体外预应力齿块构造设计

锚固端面采用3.2节局部承压设计得到的尺寸，如图6所示.根据2.3节得出的齿块锚固区局部加强方法，将锚固块设置于两个隔板之间，同时预应力筋在锚固块内进行转向，偏转角度6°，转向半径为9 m，如图7所示.

采用有限元软件ANSYS对这一方案进行线弹性分析.弹性模量E取42.6 GPa，泊松比υ取0.2，对称结构取一半进行计算，其中UHPC结构采用Solid95单元模拟，锚固集中力采用等效面荷载作用于锚垫板位置处，按27束预应力筋设计，锚固力P=4 570 kN.径向力按式（2）计算，得到F=478 kN，以均布荷载形式施加于转向处圆形管道的60°范围内.主拉应力结果如图8（a）所示，腹板外侧最大主拉应力为4.03 MPa.端部隔板应力如图8（b）所示，最大主拉应力为6.59 MPa.

3.4 锚固方案对比分析

为了进一步分析横隔板布置、预应力筋的锚固块内转向和锚固长度对锚固区局部应力的影响，对6种方案进行了计算（见图9）.其中方案1-3设置锚固块内转向，方案4-6不转向；方案2和方案5分别在方案1和方案4的基础上取消锚前隔板，方案3和方案6将锚固长度由4.1 m减小为2.7 m，锚固块没有延伸到锚前的横隔板，6种方案计算结果见表1.由表1中6种方案的计算结果对比分析隔板、锚固块内转向和锚固长度对锚固区受力的影响.

1）隔板的影响：将方案2与方案1对比、方案5与方案4对比，发现具有锚前隔板的锚固方案腹板外侧最大主拉应力明显较小.可见锚前隔板能显著减小腹板外侧“局部弯曲效应”，这与齿块传力机理相吻合.由于腹板最大主压应力也是发生在锚前腹板产生局部弯曲的部位，因此后者腹板主压应力值也明显小于前者.

2）锚固块内转向的影响：将方案5与方案2对比，方案6与方案3对比，发现转向之后腹板外侧应力值显著降低，可见锚固块内转向产生的径向力对抵抗体外索产生的偏心弯矩起到很大的作用.将方案4与方案1对比，两者锚固齿块均布置在隔板间，腹板外侧最大主拉应力值接近，但方案1锚端隔板最大主拉应力值较小，可见锚固块内转向可以使隔板分担的垂直分力减小，这对隔板的受力有利.另一方面，从锚固块体积对比可知转向之后锚固体积可以较大程度地减小，从而降低结构自重.

3）锚固长度的影响：将方案3与方案2对比，方案6与方案5对比，后者腹板外侧最大主拉应力与隔板最大主拉应力均小于前者，可见锚固长度的增加可以使局部受力更加有利，但后者体积的增加是设计时必须考虑的问题.同时还可以看出，与隔板和锚固块内转向相比，就减小“局部弯曲效应”产生的腹板外侧拉应力效果而言，利用隔板和锚固块内转向比加长齿块更加有效.

综上，方案1将锚固齿块布置在相邻两隔板之间，同时考虑预应力筋在齿块内的转向，不仅能使应力值满足设计要求，同时锚固块体积也较小，更方便了张拉施工.

4 结 论

1）揭示了体外预应力独立矩形齿块锚固区拉应力分布的4种作用效应，即“悬臂效应”，“锚后牵拉效应”，“锚下劈裂效应”和“局部弯曲效应”.当壁板厚度较小时，锚前产生的“局部弯曲效应”使壁板外侧出现较大的拉应力.

2）体外预应力筋锚固时在齿块内转向产生的径向力可以有效抵抗锚固力产生的偏心弯矩，同时也能使锚固块的体积得到减小.

3）布置于锚固齿块前后的横隔板可以极大地抵抗锚固力产生的偏心弯矩，减小因壁板厚度太小产生的“局部弯曲效应”.新型UHPC连续箱梁桥可以利用其密集横隔板结构的优势进行体外预应力的齿块锚固.方案1所示的齿块锚固构造形式降低了体外预应力锚固的偏心影响，可用于新型UHPC箱梁结构中.

4）文中对锚固结构的研究集中在构造上，旨在减小锚固结构对箱梁主体结构的削弱.今后如何针对UHPC材料特性进行局部尺寸的优化，以及针对材料与结构特点对箱梁锚固区进行配筋设计，有待进一步研究.

参考文献

[1] RICHARD P， CHEYREZY M. Composition of reactive powder concrete research[J]. Cement and Concrete Research， 1995， 25（7）： 1501-1511.

[2] DUGAT J， POUX N， BERNIER G. Mechanical properties of reactive powder concretes[J]. Materials and Structures， 1996， 29：233-240.

[3] BENJAMIN A G. Characterization of the behavior of ultra-high performance concrete[D]. Maryland： Department of Civil and Environmental Engineering， University of Maryland， College Park， 2005：16-197.

[4] BENJAMIN A G. Material property characterization of ultra-high performance concrete[R]. Washington DC： Federal Highway Administration， 2006： 167-170.

[5] 何峰， 黄政宇. 原材料对RPC强度的影响初探[J]. 湖南大学学报：自然科学版， 2001， 28（2）： 89-94.

HE Feng， HUANG Zheng-yu. Study on the effect of materials on RPC strength[J]. Journal of Hunan University： Natural Sciences， 2001， 28（2）： 89-94. （In Chinese）

[6] 邵旭东， 詹豪， 雷薇，等.超大跨径单向预应力UHPC连续箱梁桥概念设计与初步实验[J]. 土木工程学报， 2013， 46（8）：83-89.

SHAO Xu-dong， ZHAN Hao， LEI Wei，et al.Conceptual design and preliminary experiment of super-long-span continuous box-girder bridge composed of one-way prestressed UHPC [J]. China Civil Engineering Journal，2013， 46（8）： 83-89. （In Chinese）

[7] 李国平. 节段式体外预应力混凝土桥梁的构造[C] //第九届后张预应力学术交流会论文集. 北京： 中国土木工程学会， 2006：78-84.

LI Guo-ping. The structure of external prestressing segmental concrete bridges[C] //The 9th Post-Tensioned Prestressing Academic Exchanges Conference Proceedings. Beijing： China Civil Engineering Society， 2006：78-84. （In Chinese）

[8] 林波， 刘钊， 吕志涛. 体外预应力独立矩形齿块锚固区拉压杆模型及配筋设计[J]. 工程力学， 2011， 28（12）： 59-64.

LIN Bo， LIU Zhao， LV Zhi-tao. Strut-and-tie model and reinforcement design method for isolated rectangular anchor block for external tendons[J]. Engineering Mechanics， 2011， 28（12）： 59-64. （In Chinese）

[9] MLEJNEK H P， SCHIRRMACHER R. An engineers approach to optimal material distribution and shape finding computer method in applied mechanic and engineering[J]. Computer Methods Applied Mechanics and Engineering， 1993， 106（1/2）：1-26.

[10]AASHTO.LRFD bridge design specifications[S].6th ed. Washington， DC： American Association of State Highway Transportation Officials， 2012：122-125.

[11]ACI318M-11 Building code requirement for structural concrete and commentary[S]. Farmington Hills， MI： American Concrete Institute， 2011： 302-304.

[12]ZHOU Wei， HU Hai-bo， ZHENG Wen-zhong. Bearing capacity of reactive powder concrete reinforced by steel fibers [J]. Construction and Building Materials， 2013， 48：1179-1186.