合肥市PM2.5影响因素及分布演变规律的定量分析

汪雅倩，朱家明，钱舒婷，夏慧萍

(1.安徽财经大学　金融学院，安徽 蚌埠 233030；2.安徽财经大学　统计与应用数学学院，安徽 蚌埠 233030)



合肥市PM2.5影响因素及分布演变规律的定量分析

汪雅倩1，朱家明2，钱舒婷1，夏慧萍2

(1.安徽财经大学金融学院，安徽 蚌埠 233030；2.安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

摘要：针对合肥市PM2.5影响因素及分布演变规律,综合使用定量分析、相关分析、变量控制，最小曲率插值等方法，构建了简单相关系数、偏相关系数、独立性检验、单污染源高斯烟羽扩散、双源强高斯烟羽扩散等模型，运用EXCEL、EVIEWS、SPSS、SURFER、MATLAB等软件编程求解，研究得出PM2.5与PM10相关性最高、空气湿度对PM2.5有着较强影响、合肥地区PM2.5多发于春冬季、离市中心越近污染程度越大、PM2.5成因来源广泛，演变受到风力等影响的结论.

关键词：PM2.5；相关分析；独立性检验；最小曲率插值法；高斯烟羽扩散；SURFER；MATLAB

近年来，对人体有极大危害的雾霾的频发已成为一个被政府部门、人民群众广泛关注的问题.据2013年发改委报告[1]显示，受雾霾天气影响面积约占国土面积的1/4，受影响人口约6亿人.而早在2012年，空气质量指数AQI的6个基本检测指标中，就首次将产生灰霾的主要因素——细颗粒物PM2.5列入.新检测标准[2]的发布和实施，将会对空气质量的检测，改善生存环境起到重要的作用.因此，对PM2.5影响因素及分布演变规律问题的研究，对于分析减少城市污染问题和保护环境具有重要意义，同时，此研究也对其他类型污染物问题以及热源扩散、衰退有一定指导意义.

1数据来源与模型假设

合肥市2014年每天的PM2.5、PM10、CO、NO2、SO2、O3浓度数据以及2014年合肥地区一年10个观测点PM2.5数据均来源于青悦空气质量数据库[3].为了便于解决问题，提出以下假设：(1)观测点的位置在地图上选取的位置无误，用一点代表整个区的观测位置；(2)地图上观测点的测量距离测量无误；(3) 整个合肥市的PM2.5全部来源于数据库给定的10个监测点；(4)不考虑突发事件造成的空气质量突变；(5)影响大气环境的各项因素不会出现非预期的异常变化；(6)假设风速一定，且风向在一定时间内一定，不考虑突变因素、建筑物对风向的影响；(7)不考虑PM2.5的垂直分布；(8)地面及地标地物对PM2.5无吸收；(9)整个扩散过程PM2.5污染物质量守恒；(10)数据真实可靠，不考虑软件工具在数据处理及图形绘制中的误差.

2PM2.5与其影响因素相关性及独立性分析

2.1研究思路

首先建立各指标之间的相关系数表以对变量之间的相关性进行定量分析；之后着重分析PM2.5与其余5项指标之间的相关关系，为了消除指标间关系对结果的影响，使用偏相关分析控制变量，然后根据PM2.5与各指标之间相关系数大小对影响程度进行排序；最后分别对PM2.5和其余5项指标做独立性检验(卡方检验)，根据检验的Person卡方P值进行排序以验证前面结果的正确性.最后因为水是化学反应不可缺少的物质，因此有理由相信湿度与PM2.5有关，再根据分析验证湿度与PM2.5有相关性.建模流程如图1.

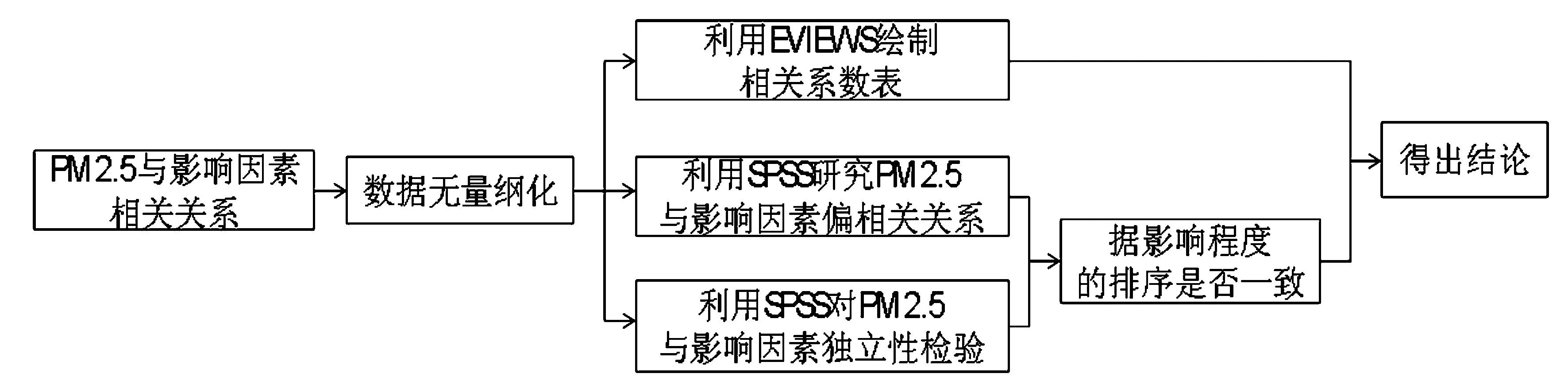
图1　PM2.5与其影响因素相关性及独立性分析流程图

2.2数据处理

根据无量纲化后合肥市2014年每天的PM2.5、PM10、CO、NO2、SO2、O3浓度数据，利用EVIEWS分析各个指标之间的简单相关关系，结果如表1所示.

表1　PM2.5与影响因素间的简单相关系数

为了针对性地刻画5个影响因素中某一个对PM2.5浓度的影响或相关程度，需将其他因素的影响视作常数(暂时不考虑其他因素影响).在此先用EVIEWS来对偏相关关系进行形象地研究，绘制出PM2.5与各影响因素的相关图，结果如图2和图3所示.

图2　PM2.5与一氧化碳(CO)的相关图　　　　　　　　　　图3　PM2.5与臭氧(O3)的相关图注：由于PM2.5与PM10、CO、NO2、SO2相关图形式相似，在此以CO为例.

用SPSS具体地刻画PM2.5与各影响因素的偏相关系数，结果如表2所示.

表2　PM2.5与影响因素的偏相关系数

利用SPSS对PM2.5与各影响因素进行独立性检验，根据Person卡方值对影响程度进行排序，从而对比于偏相关分析给出的排序，若结果大致一致，则可给出结论.

2.3结果分析

简单相关分析中，PM2.5与除O3外因素均存在一定相关关系，尤其与PM10高度相关，可能是二者粒径的差异，即PM10包含PM2.5，而粒径更小的PM2.5对人呼吸道的伤害更大.

做出独立性检验结果，与偏相关分析的结果对比，分析结果基本一致，结论如表3所示.

表3　影响程度排序表

相关研究[4]表明：SO2、NO2、CO是在一定环境条件下形成PM2.5前的主要气态物体，可以认为这些污染物在空气中通过物理和化学反应转化为了PM2.5，而水一般都是化学反应不可缺少的物质，因此有理由相信空气湿度与PM2.5有关.

据在青悦空气质量数据库收集的湿度及PM2.5数据，分别建立不含及含有空气湿度变量的线性回归模型一、二，通过模型一、二的结果比较，分析说明 PM2.5 与空气湿度的关系.

利用 EVIEWS模型一、二的显著性检验，结果如表4所示.

表4　 模型一、二结果对比

结果显示，增加空气湿度指标后，线性回归方程相关系数得到明显提升(由 0.876增加到0.916),表明空气湿度对PM2.5有较强影响.

根据上述的研究分析，可以在日常的环境保护中有针对性地进行治理，尤其是对于PM10的治理应该有所侧重，同时也应该对空气湿度进行适当的控制.

3PM2.5时空分布规律

3.1研究思路

根据合肥地区2014年一年10个观测点PM2.5数据，利用EXCEL画出监测点的PM2.5面积图，分析得出相关的时间分布规律；利用Surfer软件根据10个观测点的位置坐标以及浓度数据绘制PM2.5分布等浓度图，比较同一时间下不同观测点的PM2.5分布情况，得出空间分布规律.

3.2数据处理

对处理后数据，用EXCEL分别绘制10个检测点PM2.5时间分布图，在此以滨湖新区的时间分布为例，如图4所示.

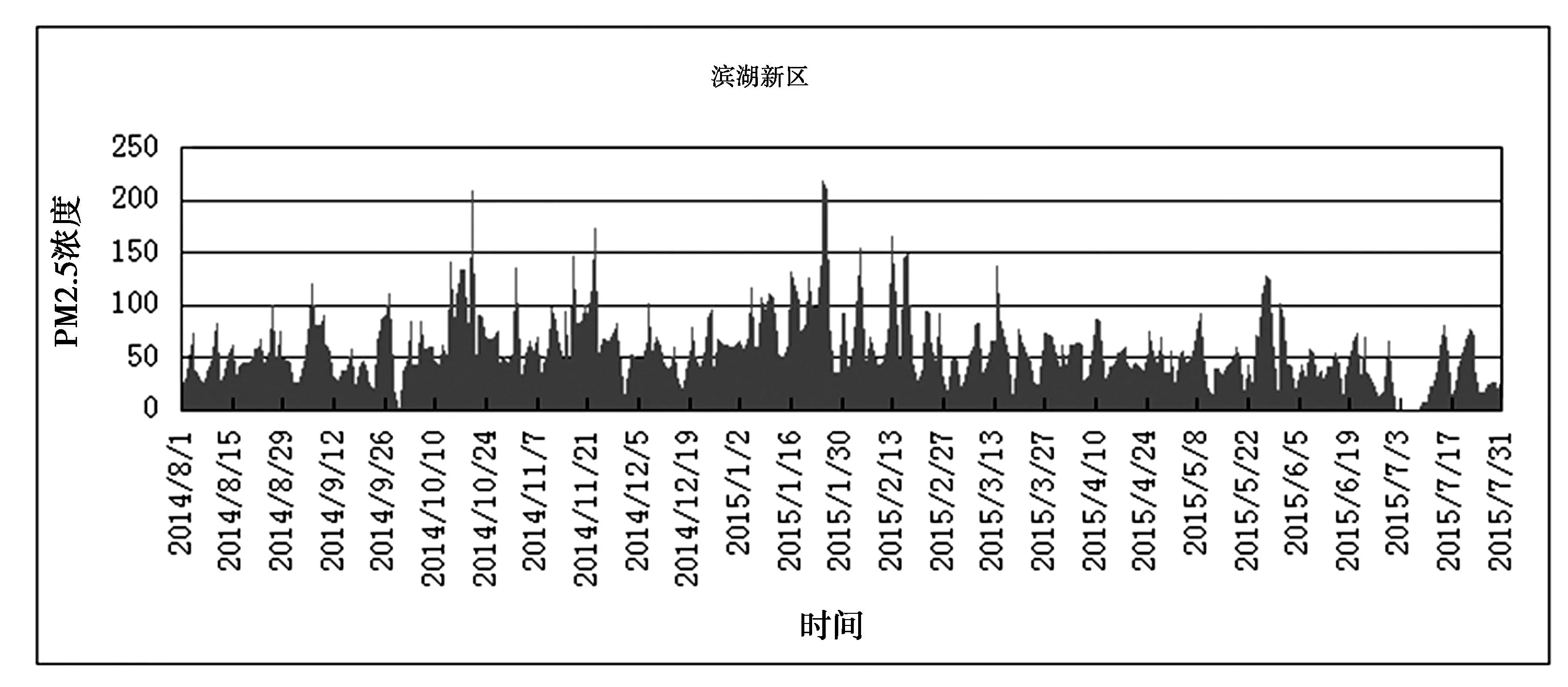
图4　滨湖新区PM2.5时间分布

将已有的数据以求和汇总的方式得到合肥10个观测点每个月的PM2.5浓度数据.根据10个监测点在地图上的分布，以最南的滨湖新区所在的水平线为X轴，最西的高新区为Y轴比较和记录观测点在地图上的空间距离测量，比较和记录观测点在地图上的空间距离测量，以X轴和Y轴所交的位置为原点建立直角坐标系，测量每个观测点的坐标，如表5所示.

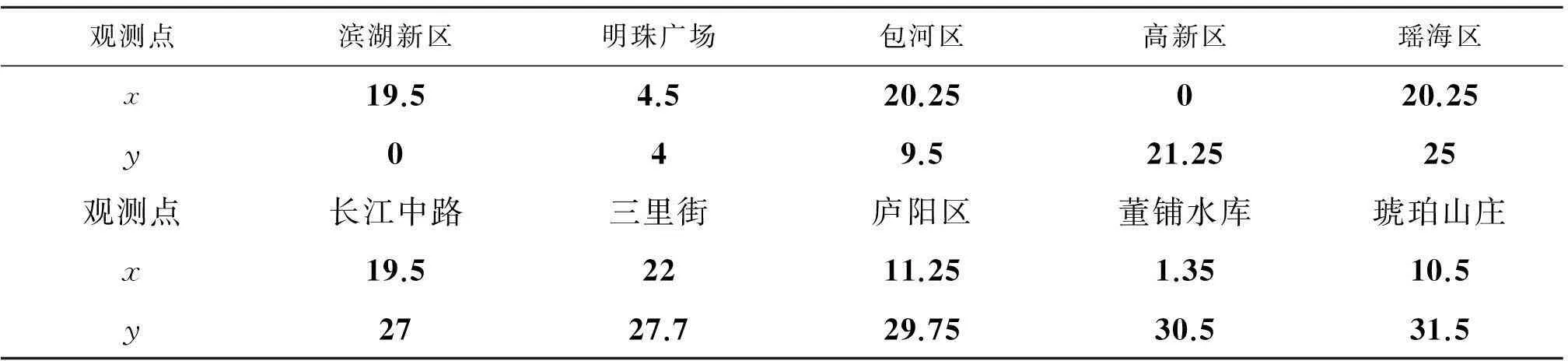
表4　10个观测点的位置坐标

(1)用Surfer绘制10个观测点的张贴图，即二维空间分布图，如图5所示.

(2)用Surfer对10个观测点位置坐标和PM2.5浓度数据进行网格化的结果，如图6所示.

图5　10个观测点的张贴图　　 　　　　　　　　　图6　2014年2月合肥PM2.5网格化结果

(3)在数据进行网格化基础上，根据最小曲率插值法[5]，利用Surfer分别对合肥10个观测点的12个月的PM2.5浓度分布绘制等浓度分布图，如组图7所示.

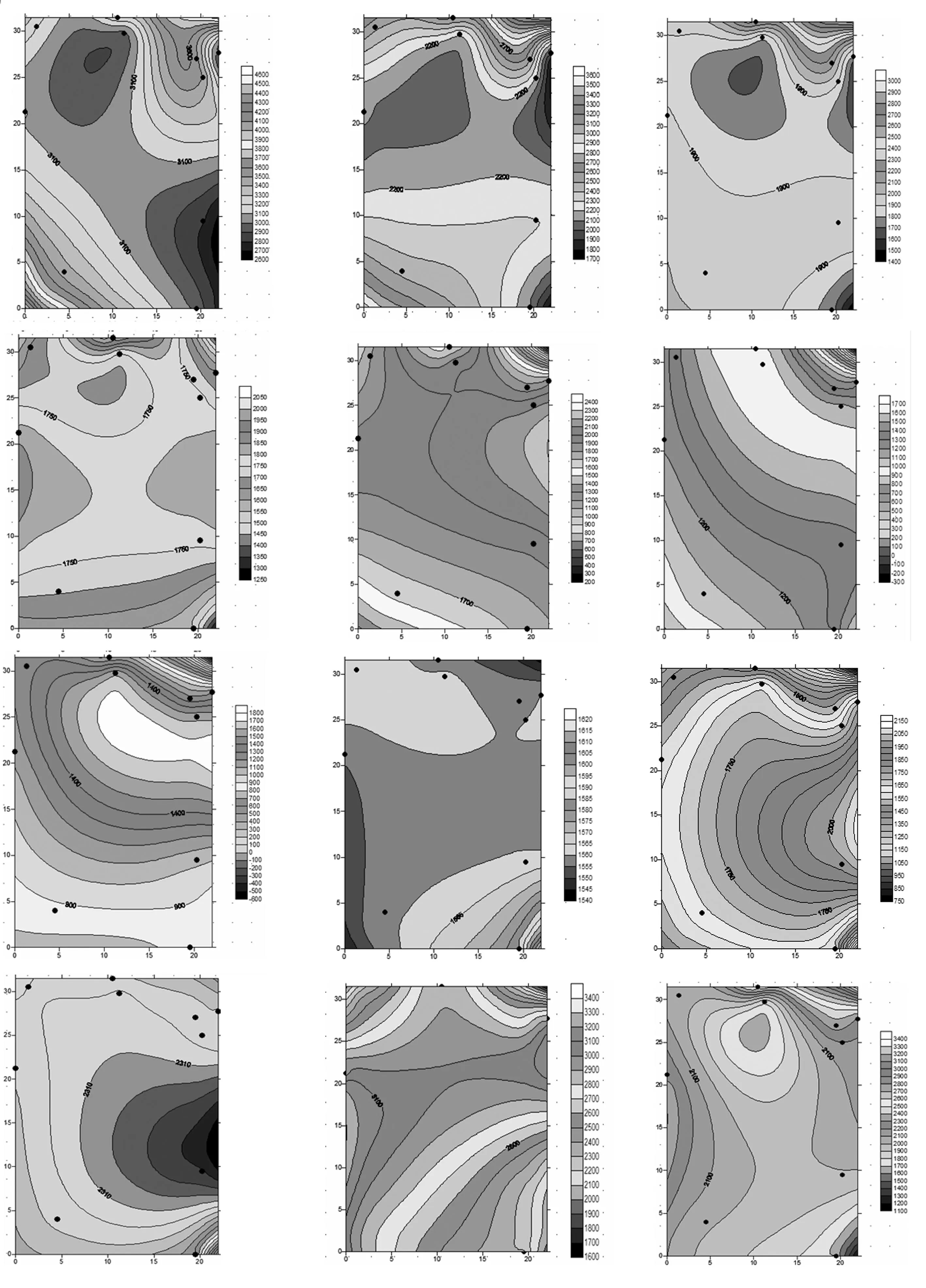
图7　PM2.5浓度分布注：组图是以时间顺序排列的，分别是2014年的12个月.

3.3结果分析

将上述分析归纳汇总，结果如表5所示.

表5　2014年12个月10个监测点的PM2.5浓度分布

在10个观测点中，其中瑶海区的空气中PM2.5含量最高，距离瑶海区较近的长江中路和三里街的观测点在12个月中PM2.5含量很高；其次是庐阳区以及距离庐阳区较近的琥珀山庄PM2.5在10个观测点中含量较高；而董铺水库、高新区、明珠广场、滨湖新区的PM2.5浓度较低.瑶海区、长江中路、三里街、庐阳区是属于合肥市中心，PM2.5来源主要是汽车尾气，二董铺水库、明珠广场、高新区距离市中心较远，位于郊区，汽车尾气较少，PM2.5的浓度较低.

4PM2.5扩散与衰减的演变规律

4.1研究思路

首先以高斯扩散原理[6]为基础，以一年天气变化最明显的7月PM2.5浓度最高的瑶海区为研究对象，分别建立单污染源PM2.5高斯烟羽扩散模型[7]，双源强高斯烟羽扩散模型[8].最后利用MATLAB对模型进行求解得到不同情况下PM2.5的污染浓度分布情况.从而探究PM2.5 的成因、演变等一般性规律.

4.2数据处理

以污染源为起点，主风向为x轴，并且指向下风的方向，与风向垂直的方向为z轴，而水平截风向为y轴的方向，则高架连续点源扩散的高斯烟羽模型公式为：

其中λy、λz为污染水平、垂直风向扩散参数，Q、h为源强、源高，σ为常数.

用MATLAB编程求解固定源强和双源强高斯烟羽扩散模型，因为三里街与瑶海区的地理位置较近，为方便研究，则以该两处监测点为例进行研究.

4.3结果分析

(1)根据合肥瑶海区 4 月份的天气状况，取大气稳定度B等级，风速为2 m/s.即λy=0.16x/(1+0.001x)0.5，λz=0.12x，由模型可知，当源强分别为持续排放达到稳态分布的固定源强时，其空气污染浓度分布如图8所示.

(2)因三里街与瑶海区的地理位置较近，所以两个观测点的PM2.5浓度会存在叠加，要高于其他地区，假定两地湿度都为87，风速为2属于B等级的天气状况，PM2.5浓度沿x,y轴的扩散系数不变.双源强PM2.5污染浓度分布如图9所示.

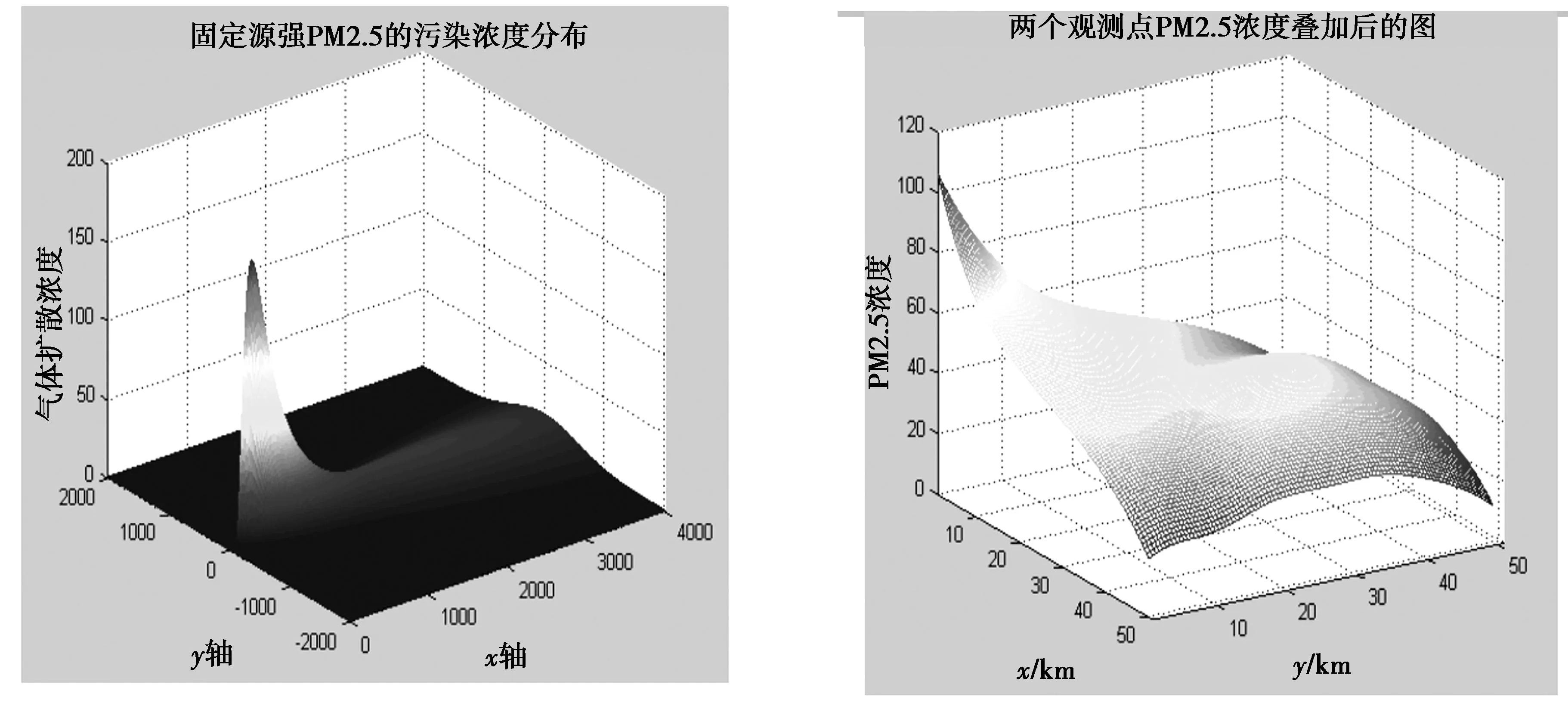
图8　固定源强PM2.5的污染浓度分布图　　　　　　 　图9　两个观测点PM2.5浓度叠加后的图

由图8可知瑶海区7月的PM2.5浓度的扩散情况在观测点1000 km以外的的区域PM2.5基本上已经对该地区没有影响了.

由图9可知PM2.5浓度分布不仅在源强出现极值，在某个下风向方向也出现了比较高的PM2.5浓度极值区域，且该区域的污染物浓度值变化较为缓慢.因为考虑到了邻近观测点PM2.5的释放对瑶海区的影响，污染扩散的速度要慢.

5总结

针对3个有关PM2.5浓度的问题，采用多种分析方法并建立相应模型进行研究，使问题得到更加全面的分析，并运用多种软件做出各类相关图形，使得数据处理、结果分析等过程更加形象易懂，从而较好地解决了合肥市PM2.5影响因素及分布演变规律问题.

参考文献:

[1]发改委.节能减排形势严峻产业发展潜力巨大报告[EB/OL].http://snap.windin.com/ns/findsnap.php?ad=0&id=204632670,2015-8-2.

[2]中华人民共和国环境保护部，环境保护标准.bz.mep.gov.cn ,2015-8-2.

[3]青悦空气质量数据库[EB/OL].http://air.epmap.org/,2015-8-2.

[4]环境保护部.环境空气气态污染物(SO2、NO2、O3、CO)连续自动监测系统运行与质控技术规范[EB/OL].http://kjs.mep.gov.cn/hjbhbz/bzwb/dqhjbh/jcgfffbz/201308/t20130802_256853.htm,2015-8-2.

[5]陈欢欢,李星,丁文秀.Surfer8.0等值线绘制中的十二种插值方法[J].工程地球物理学报,2007,4(1): 52-57.

[6]石东伟,陈东娜.高斯扩散模型在确定污染源位置中的应用[J].河南科技学院学报，2012,40(2):55-58.

[7]张斌才,赵军.大气污染扩散的高斯烟羽模型及其GIS集成研究[J].环境检测管理与技术，2008,20(5):17-19，55.

[8]李云云.高斯烟羽模型改进及在危险品泄漏事故模拟中的应用[D].广州：广州大学，2013.

[责任编辑：王军]

Quantitative analysis and distribution of Hefei PM2.5 factors of evolution

WANG Yaqian1, ZHU Jiaming2, QIAN Shuting1, XIA Huiping2

(1.School of Finance; Anhui University of Finance and Economics, Bengbu 23303, China；2.School of statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu 23303, China)

Abstract:Hefei factors for PM2.5 and distribution evolution problem, the integrated use of quantitative analysis, related analysis, variable control, minimum curvature interpolation method, construction of a simple correlation coefficient, independence test, single Gaussian plume diffusion sources, dual Source strong Gaussian plume diffusion model, using EXCEL, EVIEWS, SPSS, SURFER, MATLAB software programming to solve, research results PM2.5 and PM10 highest correlation, air humidity has a strong influence on PM2.5,Hefei area, mainly in the spring and winter PM2.5,from the city center closer the greater the degree of pollution, cause PM2.5 wide variety of sources, conclusion evolution by wind and other effects.

Key words:related analysis; independence test; minimum curvature interpolation; Gaussian plume diffusion; SURFER；MATLAB

中图分类号：X513

文献标识码：A

文章编号：1672-3600(2016)03-0001-06

通讯作者:朱家明(1973-),男,安徽泗县人,安徽财经大学副教授,硕士,数学建模实验室主任,主要从事应用数学与数学建模的研究.

基金项目：国家自然科学基金资助项目(11301001)；安徽财经大学教研项目(acjyzd201429)

收稿日期：2015-09-26