耦合电光双稳映像格子模型时空混沌的同步

刘　璐，谷开慧，孙晓冰

(长春理工大学，吉林 长春　130000)



耦合电光双稳映像格子模型时空混沌的同步

刘璐，谷开慧，孙晓冰

(长春理工大学，吉林 长春130000)

摘 要：中函数驱动技术实现了耦合双稳映象格子模型的时空混沌同步。通过理论计算可以得到两个时空混沌系统的误差表达式。画出李雅普诺夫指数。数值模拟结果表明,采用适当的参数,可以将两个耦合双稳映象格子模型实现时空混沌的同步。画出整体误差随反应时间的变化曲线。因此，函数驱动的方法可广泛用于保密通信中。

关键词：耦合电光双稳映象；时空混沌；函数驱动；整体误差

自20 世纪 90 年代 Pecora 和 Carroll[1]首次实现混沌同步以来,人们相继提出了很多混沌同步的理论方法，并且有些理论已在实验中获得了成功[ 2,3]。近些年来人们研究颇多的是时间混沌的同步，对时空混沌的同步研究的较少，且时空混沌较时间混沌更为复杂，应用的领域也大有不同，特别是在通信领域中，所以研究时空混沌不仅具有挑战性[4-6]还有一定的现实意义。本文利用函数驱动的方法从理论上较精确的计算了另个时空混沌系统的误差，数值模拟了两个耦合电光双稳系统的误差随时间和空间的变化，从而实现了两个时空混沌系统的混沌同步。

1耦合电光双稳映像格子模型

在一个包含时间和空间的系统中，我们用偏微分方程[7]来研究系统中空间所有点的状态随时间变化的规律，如：

∂tu=F(u,∂xu)

(1)

其中用u表示状态矢量，用x表示空间矢量， t表示时间变量，式(1)可表示为：

∂tu=F(u)+ε2u

(2)

可以将反应扩散过程分解为局部反应过程和扩散过程同时进行的两个过程，通过并行一个非线性映像来描述局部反映过程，扩散过程可以通过将拉普拉斯算子离散化得到，得到一维耦合映像格子模型[8]：

(3)

式中n表示离散化后的时间变量，用周期性边界条件为xn(0)=xn(L)。

2混沌同步

本文以耦合电光双稳映像格子模型为研究的对象，研究混沌同步的问题，基于Lyapunov稳定性理论，通过选择适当的驱动函数，实现时空混沌的完全同步，为了验证此种方法的有效性，采用了数值仿真的方法对其系统进行研究。

电光双稳系统模型作为我们要研究的函数：

(4)

I=6.1，k=0.8,a=π,ε=0.1，初值为0-1之间的任意一个值，耦合电光双稳映像格子模型(3)，如图1表示的是在i=1，2，3…，100格点上的最大Lyapunov指数，从图中可以看出1-100个格点中的每个格点的Lyapunov指数都是大于零，因此系统处于混沌状态，采用I=6.1，k=0.8,a=π,ε=0.1,利用函数驱动的方法研究驱动系统和响应系统的同步。其方法如下：取电光双稳系统为研究目标，利用驱动函数的方法可以将函数写成下式：

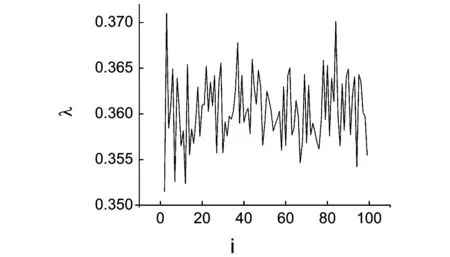
图1　K=0.8,ε=0.1时,耦合电光双稳映像格子模型所有格点的Lyapunov指数

xn+1(i)=mxn(i)+h(xn(i))

(5)

其中m表示的是控制参数，h(xn(i))表示的是选取的驱动函数，驱动函数的形式如(5)式：

(6)

另外，实现驱动和响应的同步，除了驱动系统外还用构造一个效应系统，即

yn+1(i)=myn(i)+h(xn(i))

(7)

要想实现驱动和响应同步，必须要让两个系统的状态值的差为零，所以有必要表示出驱动系统和响应系统状态值的差，成为两系统的误差值：

en(i)=xn(i)-yn(i)

(8)

因此，Lyapunov指数λ可以用两系统的误差来表示：

(9)

(10)

根据Lyapunov稳定性理论，Δλ>0，系统处于混沌态，此时驱动和响应的两个系统不能实现同步；若Δλ<0，即|m|<1即则驱动系统和响应系统实现了混沌同步，因此，选择合适的控制的取值范围，可以将Lyapunov控制在小于零的范围内，即系统实现了混沌的同步。本文系统的参数取I=6.1，k=0.8,θ=π,ε=0.1，系统反应到2 800步,xn(i),yn(i)任意取值，前2 500步都为混沌状态，并没实现同步，去掉2 400步的暂态过程，画出2 400-2 600步迭代的误差，从2 500步开始对系统进行控制并记录响应的误差，图2是控制参数取0.5时的时空演化图，由此可以看出，施加同步控制后，系统的误差变量迅速的趋于零，即两个时空混沌系统迅速实现了完全混沌同步。

图2　m=0.5时，系统误差变量随时空的演化

求误差变量的整体误差，即每个格点每一时间步的误差的完全平方的平均值，再对它进行开方，便可得到整体误差，下图3给出了控制参数m=0.8,m=-0.8,m=0.5时误差变量的整体误差，记录2 490到2 530步的整体误差，2 500步时开始控制，从图中可以看出，系统在受到控制之前，误差变量的整体误差均大于零，在2 500步给两个系统施加同步控制，整体误差迅速的降至零，根据运行的数据可得知，m=0.5时施加控制后十几步便可趋于零。

图3　m分别是-0.8，0.8，0.5时模型中所有格点的整体误差

当控制参数为0.8时，整体误差的图线与m=-0.8时的整体误差图线重合，如图中绿色的图线，图3反映了误差变量的整体误差的大小与控制参数的绝对值大小有关，与正负无关，若绝对值相同，则整体误差也相同，控制参数的绝对值越小，整体误差趋于零越迅速，图线越陡，相反的，控制参数的绝对值越大，整体误差趋于零的速度越迟缓，图像越平缓。

3结论

驱动函数的方法实现驱动系统和响应系统时空混沌的同步，有一个很重要的优势：系统对控制参数的要求不高，只要是在一定的范围内，便可实现时空混沌的同步，但是不同的参数会影响从混沌到同步的时间，因此，此种方法具有现实的意义可以将其应用到实际的系统中，特别是保密通信中。

参考文献：

[1]Pecora.L.M.and Carroll.T.L.Synchronization of chaotic systems[J].Phys.Rev.Lett,1990(64):821-832.

[2]Hegazi,AS,Ahmed,E,Matouk,AE,On chaos control and synchronization of the commensurate fractional order Liu system[J].Commumizations in nonlinear science and numerical simulation,2012,18(5):1193-1202.

[3]Rosin,David P,Rontani,et a.Control of Synchronization Patterns in Neural-like Boolean Networks[J].Phys.Rev.Lett.,2013,110(10):104102,1-5.

[4]Levy,Etgar C,Horowitz Moshe,Synchronization between two weakly coupled delay-line oscillators[J],Phys.Rev.E,2012,86(6):066209.

[5]刑朋波，宋耀良，南明凯，等.耦合蔡氏电路中混沌同步的充分必要条件[J].电路与系统学报，1998(3)：68-92.

[6]Lv J H,Zhou T S,Zhang S C.Chaos synchronization between linearly coupled chaotic systems[J].Chaos,Solitions and Fractals,2002(14):529-541.

[7]杨维明.时空混沌和耦合映像格子[M].上海：上海科技教育出版社，1994,13.

[8]卢侃等编译.混沌动力学[M].上海：上海翻译出版公司，1990:23-56.

[9]吴卫华.Lorenz混沌系统的分析与电路实现[J].大学物理实验，2014，27(2)：39-42.

Spatiotemporal Chaos Synchronization in Coupled Electrical-Optical Bistable Map Lattices System

LIU Lu,GU Kai-hui,SUN Xiao-bing

(Changchun University of Science and Technology,Jilin Changchun 130000)

Abstract：The synchronization of spatiotemporal chaos is realized by using Function drive techniques in coupled electrical-optical bistable map lattice systems.We obtain a formula of deviation for two spatiotemporal chaos systems.We draw Lyapunov exponent.Numerical simulations indicate that two spatiotemporal chaos system could be synchronized by using suitable parameter.We draw global error curve with reaction time.So,function driven method can be widely used in secure communication.

Key words：coupled electrical-optical bistable map lattice systems；spatiotemporal chaos；function drive techniques；global error

中图分类号：O 437

文献标志码：A

DOI：10.14139/j.cnki.cn22-1228.2016.001.009

文章编号：1007-2934(2016)01-0033-03

收稿日期：2015-09-12