基于有限记忆最小二乘的雷达误差配准算法

米芳彬，徐小刚，梁　健

(中国电子科技集团公司第五十四研究所，河北 石家庄050081)



基于有限记忆最小二乘的雷达误差配准算法

米芳彬，徐小刚，梁健

(中国电子科技集团公司第五十四研究所，河北 石家庄050081)

摘要针对非合作目标多雷达组网中的系统误差配准问题，介绍了基于地心地固坐标系的三维空间配准模型，以及常用的雷达误差配准方法——最小二乘法。为了能够实时估计出系统偏差，并解决最小二乘等批处理算法在求解系统误差过程中数据量、计算量和存储量随时间递增的问题，提出了基于广义最小二乘法的有限记忆最小二乘法。通过一个实例，对新算法进行Matlab仿真，结果证明了算法的正确性和有效性。

关键词非合作目标；误差配准；最小二乘法；雷达组网

An Algorithm of Radar Registration Based on Finite Memory Least Squares

MI Fang-bin,XU Xiao-gang,LIANG Jian

(The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)

AbstractIn view of the registration problem of non-cooperative target multi-radar networking,this paper introduces a three-dimension space registration model based on earth center earth Fixed coordinate system and the least squares method used frequently in radar registration.Based on generalized least squares method,a finite memory least squares method is proposed to estimate the real-time system deviation,and improve the increment over time of data size,calculation amount and memory space during the computing of system deviation for least squares method and other batch algorithms.The Matlab simulation results prove the accuracy and availability of this algorithm.

Key wordsnon-cooperative target;registration;least squares method;radar networking

0引言

现代信息化战争中，信息的高复杂性和高多样性是侦察探测系统面临的难题之一，雷达组网系统的出现有效地解决了这一问题[1,2]。雷达组网中的多雷达协同工作、性能互补的优势突破了单一雷达的局限性，提高了侦察系统的探测精度和可靠性。但未经误差配准的雷达会因为其本身的量测偏差和探测中随机误差的存在导致错误的观测，进而引起态势混乱[3]。

侦测系统中随机误差可以通过滤波的方法进行消除或者依据统计特性设法削弱其对测量结果的影响；但量测偏差属于确定性误差，无法经滤波方法消除[1,4]。在一定条件下，检飞和标校[5,6]等手段可对量测偏差予以不同程度的降低，但仍会残留系统误差。通过建立系统误差求解模型，计算量测数据可对残留系统误差进行粗略估计。但随着时间的推移，在各种内外在原因的影响下，雷达系统误差可能又重新生长，因此必须研究可在实际运行过程中实时进行雷达空间配准的算法。

常用的误差配准方法有实时质量控制算法[7]、最小二乘法[8,9]以及最大似然法等。文献[8]采用基于球(极)投影的广义最小二乘法(GLS)实现了二维空间的误差配准，该方法不能估算出雷达的俯仰角偏差。文献[9]采用基于地心地固(ECEF)坐标系的GLS算法实现了多雷达斜距、方位角和俯仰角的偏差估计，该方法未能实现实时的误差估计。在侦测过程中，上述算法的计算量将随着时间的增长而增大，从而影响计算速度[10,11]。本文在GLS算法的基础上提出一种基于有限记忆的广义最小二乘法，该方法能实时地估计出量测偏差，减少系统的计算量。

1问题的描述

以传统的三坐标雷达为研究对象[12]，并假定雷达的位置已知且固定不变。雷达的系统误差附着在雷达对目标的测量参数上，主要有径向距离测量误差Δr、方位角测量误差Δθ和俯仰角测量误差Δη，由此可以得出误差的表达式：

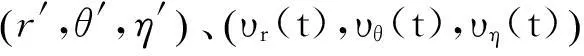
2模型的建立与算法推导

2.1坐标变换关系

下面以雷达A为例介绍地理坐标和局部坐标向ECEF坐标的转换。

雷达A的量测值(rA(k),θA(k),ηA(k))T转换为局部笛卡尔坐标系量测值：

则目标由局部笛卡尔坐标向ECEF坐标转换，公式如下：

2.2算法推导

将雷达A和B对同一目标的观测值转换到局部笛卡尔坐标系：

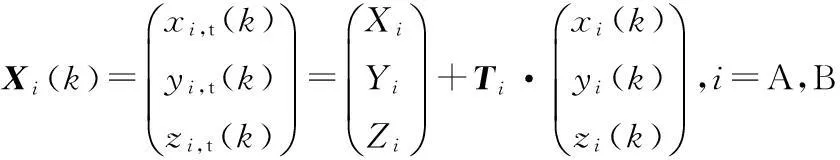
设ΔX(k)表示2部雷达在ECEF坐标系下对目标观测值的差值，则有

ΔX(k)=XA(k)-XB(k)，

f(β,ψ)≈[TA×LA(k),-TB×LB(k)]β+

[TA×JA(k),-TB×JB(k)]ψ(k)。

上式中Ji和Li表达式如下：

取C(k)=[TA×LA(k),-TB×LB(k)]，H(k)=[TA×JA(k),-TB×JB(k)]，则有

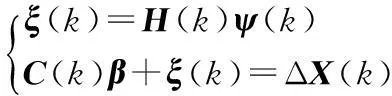
式中，ΔX(k)为雷达A和B在ECEF坐标系下对目标观测值之差；对于单一的量测，上式的解不是唯一的，需要更多的目标报告。当有N(N>1)个观测值时，上式可以表示为：

Cβ+ξ=ΔX。

依据最小二乘估计可得：

式中，Σ=E[ξξT]，此时在系统误差的求解过程中采用的观测量为N。随着时间的递增，计算量增加，导致系统存储负担增大，所以考虑每次求解过程值采用当前N个时刻的观测量，即有限记忆最小二乘法。此时系统误差的求解方程变为：

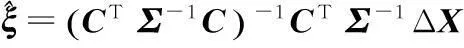
式中，各参数如下：

由于Σ为分块对角阵[3,5]，因此可以将求解方程分解为若干小型矩阵运算，进一步提升运算速度，分解式如下：

3算法仿真

针对提出的算法，采用基于ECEF坐标系的系统模型进行仿真，仿真30次，以验证算法的有效性。假设雷达A和B的地理坐标分别为：(68.923°，-137.2 589°，50.655 m)和(70.171 4°，-124.725°，217.724 4 m)。选用WGS-84坐标系，则有a=637 813 7 m，b=635 675 2 m。雷达A和B的量测精度取值分别为：

系统偏差：斜距偏差、俯仰角偏差及方位角偏差取值分别为：

以雷达A的局部笛卡尔坐标系为参考坐标系生成用于配准的航迹：

采用有限记忆最小二乘法的仿真结果如图1、图2和图3所示，分别给出了采用不同步长进行求解时，径向距离误差、方位角误差及俯仰角误差的均方根误差(RMSE)。

图1　径向距离误差的RMSE

图2　方位角误差的RMSE

由系统误差的RMSE值可以看出，步长值N取500左右时即可满足收敛条件。

图3　俯仰角误差的RMSE

步长为500时，不同时刻的径向距离、方位角及俯仰角估计偏差如图4、图5和图6所示。

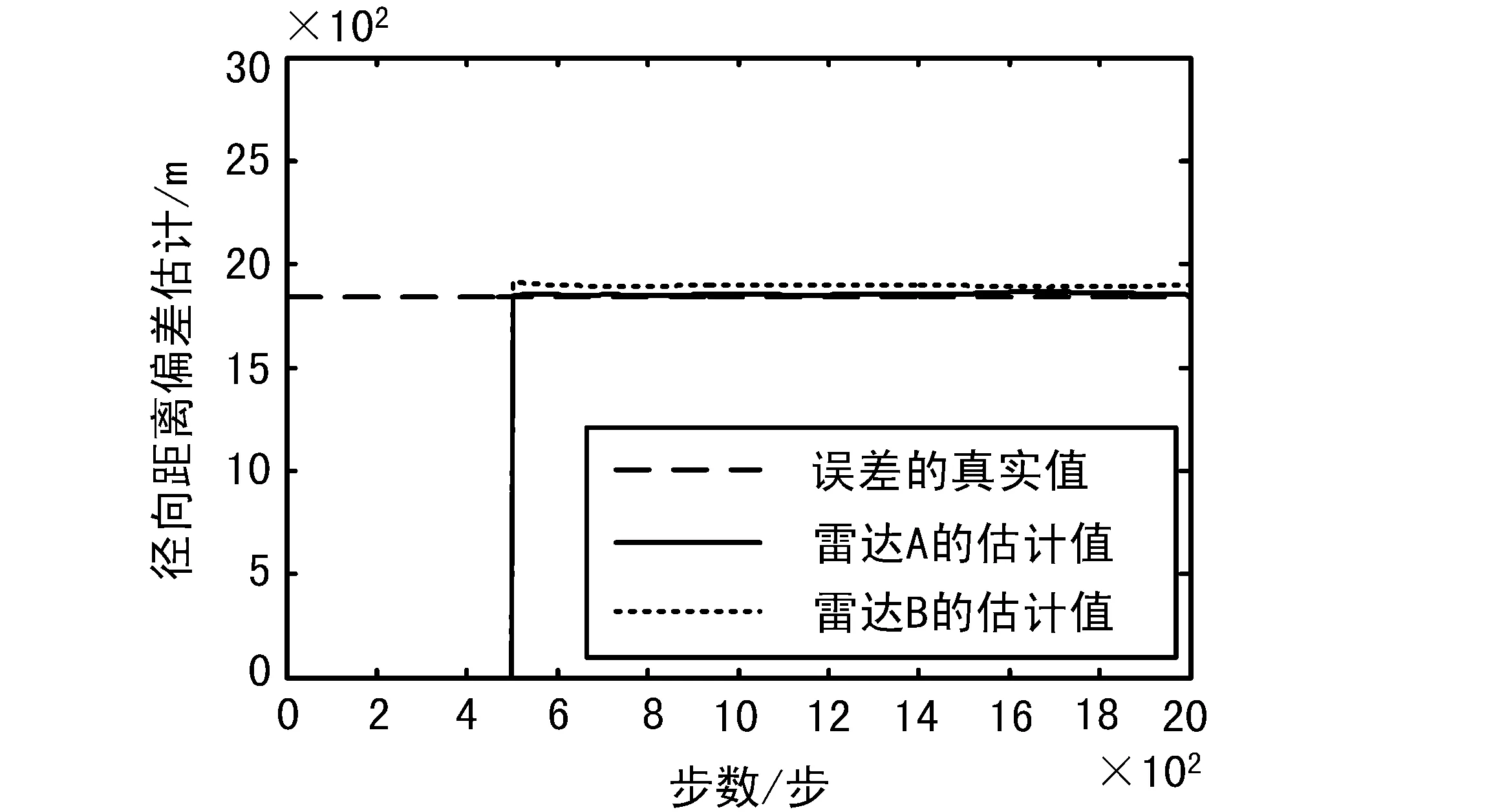
图4　雷达A、B的径向距离偏差估计

图5　雷达A、B的方位角偏差估计

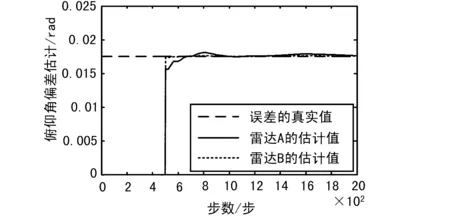
图6　雷达A、B的俯仰角偏差估计

可以看出从500步开始，算法误差估计值即收敛到误差真实值处，实现了实时准确的误差估计。

4结束语

系统误差求解是雷达空间配准的关键。结合最小二乘法，提出了基于有限记忆的误差配准算法。相比于广义最小二乘法，该算法在每次迭代运算中只采用当前时刻的若干数据进行求解，即以较小的计算量收敛到误差真实值处，且该算法能够满足雷达空间配准的实时性需求。基于理论分析和Matlab仿真结果，给出了均方根误差随数据个数的变化情况，以及系统误差随步数的收敛情况，可指导实际应用，具有一定的工程应用价值。

参考文献

[1]赵宗贵，熊朝华，王珂，等.信息融合概念方法与应用[M].北京：国防工业出版社，2012.

[2]常超伟，牛竹云，谈鹏.多雷达组网信息融合系统空间配准方法研究[J].计算机与数字工程，2013，282(4)：546-548.

[3]宋志群.认知无线电技术及应用[J].无线电通信技术，2012，38(5)：1-5.

[4]何友，修建娟，张静炜，等.雷达数据处理及应用(第二版)[M].北京：电子工业出版社，2009.

[5]邓志鑫.阵列误差对Capon波束形成算法的影响分析[J]. 无线电通信技术，2012，38(2)：41-43.

[6]于开勇，李静芳，潘申富.载波相位误差对解调性能的影响分析[J]. 无线电通信技术，2014，40(1)：26-27.

[7]宋文彬.传感器数据空间配准算法研究进展[J].传感器与微系统，2012，31(8)：5-8.

[8]SHALOM Y B.Multitarget Multisensor Tracking:Advanced Applications [M].Boston:Aretch House,1990.

[9]董云龙，何友，王国宏，等.基于ECEF的广义最小二乘误差配准技术[J].航空学报，2006，27(3)：463-467.

[10]常超伟，牛竹云，胡小珍.一种新的实时在线的空间配准方法[C]∥第三届中国信息融合大会，2011：424-428.

[11]赵杰，江晶.基于序贯最小二乘的雷达组网误差配准方法[J].空军雷达学院学报，2007，21(2)：85-87.

[12]闫俊，石韬.多传感器配准估计方法与实现[J].电光与控制，2008，15(6)：61-65.

[13]折晓宇.多源信息协同处理与融合方法[D].西安：西安电子科技大学，2014.

米芳彬男，(1991—)，硕士研究生。主要研究方向：信号与信息处理。

作者简介

中图分类号TN95

文献标识码A

文章编号1003-3106(2016)02-0065-04

基金项目：国家部委基金资助项目。

收稿日期：2015-11-09

doi:10.3969/j.issn.1003-3106.2016.02.16 徐小刚男，(1972—)，研究员。主要研究方向：航天资源任务规划。10.3969/j.issn.1003-3106.2016.02.17

引用格式：米芳彬,徐小刚,梁健.基于有限记忆最小二乘的雷达误差配准算法[J].无线电工程,2016,46(2):65-68.