基于常规波束合成的分裂阵互谱定向研究

2016-04-07 05:56:59王晓庆陈卫东

无线电工程 2016年2期

李　晋，王晓庆，陈卫东

(中国电子科技集团公司第五十四研究所，河北石家庄 050081)

基于常规波束合成的分裂阵互谱定向研究

李晋，王晓庆，陈卫东

(中国电子科技集团公司第五十四研究所，河北石家庄 050081)

摘要基于常规波束合成的分裂阵互谱测向算法是目前广泛应用的被动阵列精确测向技术。目前，常规的分裂阵互谱定向算法在实际的水下阵列布阵形式下可探测的频率范围较小，不能满足实际需求，在工程应用的角度，算法结构还有改进的空间。通过理论分析和仿真，在原有理论框架的基础上，改进了算法的流程和结构，形成了2种改进的定向算法。仿真结果表明，改进算法的精度高于阵元直接相关法，证明了改进算法的有效性，为实际工程应用提供了新的思路和理论参考。

关键词常规波束合成；测向；分裂阵

Research on Cross-spectrum Direction-finding with Splitting Beam Based on Conventional Beam-forming

LI Jin,WANG Xiao-qing,CHEN Wei-dong

(The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)

AbstractCross-spectrum direction-finding with splitting beam based on conventional beam-forming(CBF)is a widely used algorithm in accurate passive direction-finding.The existing conventional algorithm has a narrow processing band of frequency,which can′t be used in practical engineering.A research has been conducted to propose modified algorithms through theoretical analysis and simulation based on the conventional algorithm.The two modified algorithms provide new direction and theoretical reference for practical application of engineering.

Key wordsCBF;direction-finding;split array

0引言

水下目标辐射源精确定向是水下探测的主要任务之一。声呐技术发展之初，水下目标定向方法主要是利用干涉仪原理的直接相关法，其测向精度较低，不能满足实际的需求。20世纪60年代出现的波束合成技术[1]较之前者，精度得到了进一步提高，由于瑞利限的限制，在低频段其定向精度仍不尽如人意。20世纪80年代提出的高分辨力DOA估计方法[1]，例如Capon、MUSIC、ESPRIT和线性预测等算法，在高信噪比及白噪声背景下均具有较高的精度，缺点是对噪声背景较为敏感，算法中的矩阵求逆和特征分解运算量巨大，不易实现对目标的实时跟踪和处理。上述算法的一些改进算法或是计算流程复杂，或是对使用背景和探测对象有着严格的要求，在工程应用中都受到了限制。同时期，Piersol和Bendat提出了基于分裂阵的互谱法，在数字波束系统中不需要增加太大的运算量即可显著提高系统测向精度[2]。根据文献[3]，线列阵分裂波束测向算法的精度可接近于CRB下界；其频域处理和宽、窄带通用的特点也适应于数字多波束系统框架，因此在水下探测和目标识别领域应用广泛[4-6]。

本文阐述了基于常规波束合成的分裂阵互谱定向算法的基本原理，并对算法的实用性进行了分析。针对常规算法在实际应用中处理频带较小的缺点，从改变等效阵元位置和解角模糊处理2个方向提出了改进方法，从而扩展了算法可处理的频率范围。最后通过对仿真结果的分析，表明该算法的有效性及工程实用性。

1阵列信号数学模型

理想条件下，在建立阵列信号数学模型时有如下假设[8]：

① 不存在阵列误差，即阵列为标准的等距线阵(ULA)；

② 信号与噪声之间统计独立；

③ 噪声为高斯白噪声；

④ 阵元近似为点阵元，各阵元幅频特性均相同。

阵列接收信号原理图如图1所示。

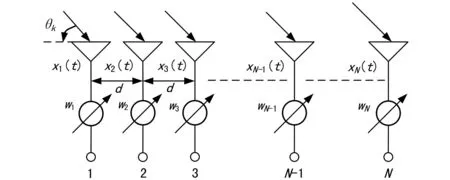
图1　阵列接收信号原理

考虑K个非相干窄带信号，在传播距离足够远的条件下，近似为平面波并以入射角度θi(i=1,2…,K)到达传感器阵列(0°≤θi≤180°)，设传感器阵列由N个阵元组成(N为偶数)，阵元间距d=λ/2，λ为阵列中心频率对应的波长，则阵列在t时刻的输入可以表示为[7]：

X(t)=AS(t)+N(t)。

(1)

式中，X(t)=[x1(t)x2(t)…xN(t)]T为阵列接收信号矢量；S(t)为入射的空间信号矢量，有S(t)=[s1(t)s2(t)…sK(t)]T；N(t)=[n1(t)n2(t)…nN(t)]T为加性噪声矢量；A为各信号导向矢量组成的N×K阶矩阵，有A=[a(θ1)a(θ2)…a(θK)]。

对于时域的常规波束合成(CBF)，阵列的输可以表示为：

(2)

以矢量来表示各阵元输出和加权矢量，阵列输出y(t,θ)可以表示为：

y(t,θ)=aH(θ)X(t)。

(3)

频域波束合成通过快速傅里叶变换(FFT)完成，设阵列在一段时间(t=t1,t2,…,tm)所得的m次连续快拍为：

(4)

对其中每个阵元的数据均进行m点FFT运算可得：

(5)

X_f中对应信号频率的一列为信号的一次频域快拍，对其进行常规波束合成(CBF)，输出可表示为：

y(fi,θ)=a(fi,θ)HX_ f(fi)。

(6)

式中，X_f(fi)=[x1(fi)x2(fi)…xN(fi)]T，i=1,2,…,m。

基于以上阵列信号处理模型，本文将介绍常规分裂阵互谱测向算法的基本原理，并对算法的流程和结构进行改进。

2常规分裂阵互谱测向算法

基于分裂阵的互谱测向算法是以常规波束合成(CBF)为基础的互谱处理，通过互功率谱计算，利用时延值反推目标角度估计值[3]。

2.1算法原理

分裂阵互谱定向算法将传感器阵列分为2个子阵，子阵划分的方式如图2所示。

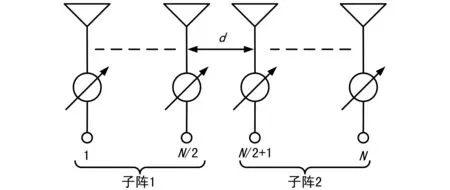
图2　子阵划分示意

以图2方式为例，假设有一窄带信号，来波方向准确值为θ，中心角频率为ω，并假定频率估计准确，波束合成能量检测输出的角度值为θCBF。根据以上信息将阵列快拍数据经过时域CBF合成为2个等效阵元的输出，2个子阵分别选择第1个和第N/2+1个阵元作为等效阵元，因此等效阵元间距为d′=Nd/2，上述2个子阵的CBF权向量同为：

(7)

2个子阵在θCBF方向的CBF输出序列为：

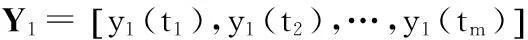
(8)

(9)

对上述输出进行m点FFT运算可得：

(10)

(11)

根据文献[3,10]，上述2组频域输出在角频率为ω处有如下关系：

(12)

(13)

从而有相位差φ：

(14)

即可由下式对来波角度进行估计：

(15)

(16)

对于目标跟踪方式下，可以根据多次测量计算周期平均角度估计值。

总结上述流程，可得基于常规波束合成的分裂阵互谱算法结构如图3所示[10]。

图3　常规分裂阵互谱测向流程

2.2算法实用性分析

算法的复杂度以及参数与实际的匹配程度，决定了算法的实用性，分析算法实用性对算法的工程应用具有重要意义。

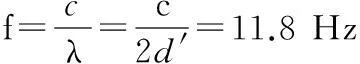
(1)

对于频率大于上述最小频率f的目标信号，在一定的来波方向上，2个子阵的时域CBF输出的相位差超过一个周期。由于cos函数的周期性，FFT及互谱运算无法准确给出2路输出相位差，也就不能准确估计来波方向，此时即文献[12]所描述的时延值为多值函数的情况。由上述计算的最大可测量频率知，算法在常用布阵形式下实用性并不高。可探索算法的改进方法以扩展可探测频率范围，提高算法的工程实用性。

3改进的分裂阵互谱算法

根据上述分析，算法在常用布阵形式下的可测量频率范围较低。以算法实用性为考虑，还有需要改进的方面。经分析，主要有以下2个改进思路。

3.1缩小等效阵元间距

根据阵列信号处理的基本原理可知，缩小阵列的阵元间距，可以扩展阵列可测量信号的频率范围。由此推知，可通过增加子阵等效阵元间距来扩展算法的测量频率范围。

不妨令等效阵元间距为可实现的最小值，即在图2的划分方式下，2个子阵分别取第N/2个和第N/2+1个阵元作为等效阵元，此时等效阵元间距为d′=d。为方便分析及处理，以频域波束合成为处理方法，2个子阵的CBF权向量为：

(17)

(18)

在无噪声条件下，对频域快拍数据中频率ω对应项进行CBF可得2个子阵输出y1(ω)和y2(ω)分别为：

(19)

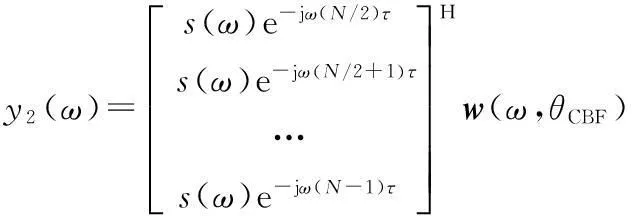
(20)

显然，y1(ω)和y2(ω)有如下关系：

y1(ω)=y2(ω)ejφ，

(21)

且有

(22)

(23)

对上述方法进行分析可得，当等效阵元间距d=1.0 m，阵元数为128时，算法可测量的最大频率为：

(1)

由上述分析可知，算法可测量频率范围与阵列可处理频率范围相匹配，算法实用性进一步提高。

综上，可得基于缩小等效阵元间距的改进算法基本流程如下：

① 以图2的子阵划分方式，取第N/2个和第N/2+1个阵元作为等效阵元，对阵列接收数据进行频域的常规波束合成；

② 以式(13)形式对2路CBF输出进行互谱运算，得到相位差φ；

3.2补偿相位模糊

由2.2节的分析可知，当等效阵元间距大于测量频率半波长时，2个子阵的CBF输出对应频率分量的相位差可能大于一个周期，FFT及互谱运算无法准确的计算这个相位差值，计算结果就产生了多个可能的相位差，且相互差2π，如果能够准确地恢复出输出相位差，那么就可以抵消阵元间距过大的影响。

在存在上述相位模糊的情况下，假设经FFT频谱运算的相位差为φ，且-2π≤φ≤2π，有

(24)

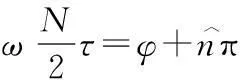
(25)

设有一128元阵列，阵元间距d=1.0 m，以图2描述的子阵划分方式，以第1个和N/2+1个阵元作为两个子阵的等效阵元，可得形如表1的相位补偿表。

表1　相位补偿表示例

由表1可见，当能量检测器输出值θCBF在补偿参数对应角度范围内时，可利用对应的n值进行相位补偿。

综上，可得基于补偿相位模糊的改进算法基本流程如下：

① 以图2的子阵划分方式，取第1个和N/2+1个阵元作为2个子阵的等效阵元，对阵列接收数据进行频域的常规波束合成；

② 以式(13)形式对两路CBF输出进行互谱运算；

④ 由式(25)及计算补偿后的互谱相位差φ；

4算法仿真与分析

为比较研究上述2种改进算法的性能，对2种算法分别进行仿真。设以128元阵列接收一个远场窄带信号，阵元间距d=1.0 m，来波方向为θ=30°，中心频率300 Hz，能量检测器输出值θCBF=27°，接收机带宽290~320 Hz，带内信噪比SNR=-30 dB，以图2方式划分子阵，对其进行129次角度估计。子阵的CBF波束如图4所示。3.1节第1种改进方法的仿真结果如图5所示，3.2节第2种改进方法的仿真结果如图6所示。

图4　子阵CBF波束

图5　第1种改进方法仿真结果

图6　第2种改进方法仿真结果

由图4中CBF波束的分析可知，来波方向θ包含在子阵形成的波束主瓣内，使期望信号获得较大的指向性增益，减小噪声和干扰对互谱计算的影响。由图5和图6可见，2种改进算法的估计性能差异较小，不易观察。在不改变其他参数的情况下，以直接相关法作为参照，调整不同信噪比(-30 dB≤SNR≤-10 dB)，以角度估计的均方根误差(RMSE)为指标，进行了500次重复实验以比较性能差异，仿真结果如图7所示。

图7　重复对比实验结果

由图7可以看出，2种改进方法的性能均比两阵元直接相关法要高，2种改进方法的处理精度相差较小。综上仿真结果可得，2种改进方法在处理精度方面是满足需求的，结合算法处理频率范围的扩展，证明了改进方法的有效性。

5结束语

分裂阵互谱定向法是精确测向系统的组成部分，对算法实用性的改进是算法工程应用中的重要内容。本文所提出的2种改进算法相比常规分裂阵互谱算法，在保证测向性能的前提下，扩展了可处理的频率范围，仿真结果表明了改进算法的有效性。为算法的工程应用提供了理论参考依据。

参考文献

[1]武思军.稳健的自适应波束形成算法研究[D].哈尔滨：哈尔滨工程大学博士论文，2005.

[2]梁国龙,江峰,蔡平.一种新颖的短线阵高精度定位系统[J].应用声学,1999，18(5):15-18.

[3]李启虎.声呐信号处理引论[M].北京:科学出版社,2012：243-244.

[4]GOU Yan-ni,WANG Ying-min.The Cross-Spectrum Approach for Underwater Multi-target Direction Estimation[J].2011 International Conference of Information Technology,Computer Engineering and Management Sciences,2011(9)：354-357.

[5]汪新,王明洲,李忠.分裂波束双通道方位走向的空间模糊问题[J].声学技术,2013，32(4):290-293.

[6]刘朝晖,付战平,王明洲.基于方位走向法和互谱法的水中目标识别[J].兵工学报,2006,27(5):932-935.

[7]夏辉,王晓庆.基于稀疏成分分析的测向技术[J].无线电工程,2014,44(10):43-46.

[8]田坦.声呐技术(第2版)[M].哈尔滨:哈尔滨工程大学出版社,2009.

[9]李福昌.宽带测向算法研究[D].哈尔滨：哈尔滨工程大学博士论文,2005.

[10]李启虎,朴大志.微弱信号源的和波束定向方法与分裂波束定向方法的性能比较[J].应用声学,2007,26(3):129-134.

[11]陈韶华,田荣艳,郑伟.线阵分裂波束相关测向测距技术研究[J].水雷战与舰船防护,2008,16(1):1-4.

[12]王正义,马进.二基元互谱定向有关问题研究[J].电子技术,2010(4)：17-19.

李晋男，(1990—)，在读研究生。主要研究方向：阵列信号处理。

王晓庆男，(1987—)，硕士，助理工程师。主要研究方向：阵列测向。

作者简介

中图分类号TN 911.7