思考无边界 实践有方向——关于问题驱动式教学的几点基本认识
江苏海安县实验小学(226600)储冬生
思考无边界实践有方向——关于问题驱动式教学的几点基本认识
江苏海安县实验小学(226600)储冬生
[摘要]问题驱动式教学是指,教师精心规划数学教学任务,设计以学科内容本质和儿童认知特质为两翼的课程核心问题,以启发学生开展数学学习活动,引导学生利用必要的课程资源通过自主、合作、探究学习获得知识建构和能力提升。问题驱动式教学是一种促进学生优质化发展的相对稳定的教学策略。
[关键词]问题驱动问题驱动教学
一、生动且深刻的教学追求
小学数学教学应当努力追寻一种“生动且深刻”的境界。“生动”是外显的形式,源自儿童内心的召唤,是由儿童的认知规律和年龄特征决定的。“深刻”则是内隐的本质,源自数学学科内在的需求,是由数学的学科特质和本质属性决定的。数学犹如核桃,核桃的外壳褶皱坚硬,内仁却味美而健脑。数学也一样,初看不一定可爱,但是细细品味却能发现它对于人的发展是极具价值的。核桃好吃壳难开,如果把整个核桃硬生生塞进嘴里,不仅难以品尝到核桃味美营养的内仁,而且坚硬晦涩的外壳会令人无法忍受。同样的道理,如果将数学硬生生地塞给学生,学生不但品尝不到数学的生动之美,还会因无法忍受而拒之千里。
我们坚定地认为小学数学教学应当努力追寻一种“生动”基础上的“深刻”,提出这样的观念,还有一个现实的背景。我校是一所百年老校,有着较为深厚的教学底蕴,数学更是学校的品牌学科之一,在省内外都具有一定的影响力,先后走出了多位国内知名的数学特级教师。我校的数学教学一直倡导“有深度”的课堂,教学设计和实施都很重视学科特质的凸显。比较而言,在课堂的鲜活灵动上,似乎还做得还不够,总显得有些“凝重有余”而“活泼不够”。所以,从学校的实际出发,我们的数学教学应该进一步凸显生动,强调鲜活,关注“童化”。
写到这里,突然想起吴正宪老师说的“让儿童享受‘好吃’且‘有营养’的数学”,不正是这个意思吗?既要“好吃”又要“有营养”,而且首先是“好吃”。“有营养”但是“不好吃”的东西学生愿意吃吗?学生能坚持天天吃吗?……如何才能让教学达到这种“生动且深刻”的理想境界呢?能否从操作层面提出自己的数学学科教学主张(或者教学模式)呢?李吉林老师的“情境教育”流派,李庾南老师的“自学·议论·引导”模式,邱学华老师的“尝试教学”主张……表述都很清晰,让人一看就能明白个大概:情境教育需要创设丰富的情境,“自学·议论·引导”模式需要有效先学,“尝试教学”需要放手让学生大胆尝试……好的教学主张一定是浅显的、易操作的,带有教学模式的特质。基于以上的思考,我们尝试提出“问题驱动式教学”的主张,倡导建构一种以核心问题为导向的教学范式。“问题驱动”的提法则源自张奠宙先生提出的数学教育的四条特有原则:数学化的原则、适度形式化的原则、问题驱动的原则、提炼数学思想方法的原则。问题驱动式教学的提出就是为了让我们的教学追求落到实处,使我们的教学理念能够在一定的范围内推广、分享,能够和一群志同道合的人携手前行。
二、问题驱动式的教学探索
上海市教科院杨玉东博士和南京师范大学徐文彬教授曾以“本原问题驱动课堂教学”为主要观点做过相关研究,探讨如何在学科本质问题驱动下设计和实施教学。他们的研究以中学数学学科为例,兼顾中学物理、化学、生物等理科教学,偏重于理论研究。在小学领域尚未有人系统关注“问题驱动式小学数学课堂教学的实践研究”,但也存在一些与此研究有内在关联,且值得借鉴和比较的项目,如:华东师范大学孔企平教授提出的“大步提问的教学观念”,广东省小学数学特级教师黄爱华提出的“以‘大问题’为导向的课堂教学变革”,上海市小学数学特级教师潘小明提出的“基于‘问题解决’的课堂转型”,等等。
问题是有意识地寻求某一适当的行动以便达到一个被清楚地意识到但又不能立即达到的目的。从某种意义上看,问题就是困难。如果说问题是一种困难,那么学习便是一种发现困难、解决困难的过程,教学就是一种有意识地消解困难或者设置困难的过程。问题的存在最能激发人的思维或行动动机。问题作为一种认知情境,通常应具备三个要素:(1)未知事物:“全然不知”不会引起注意,“熟知事物”可以注意但不会长久,“知道与不知的混合物”才会引起学生强烈的学习兴趣和积极的探究活动;(2)思维动机:人都有填补认知空缺和解决认知失衡的需要;(3)认知水平:问题必须让学生在已经达到的知识水平上觉察到,但学生仅凭这些知识经验仍无法解决问题,这就是思维的开端。
问题驱动是指在小学数学课堂教学中设计并形成系列的、环环相扣的问题,把学生的思维探究引向深处,从而最大限度地激发他们体验和理解数学学习内容的本质,让他们形成良好的数学素养。问题驱动是基于学科教学设计的角度提出的,“问题”是人类好奇心的表现,也是激发学生学习数学的原动力。在这个含义下,问题的产生至少有两个方面:一是教师在备课过程中精心设计的,既能够反映课程内容本质,又能促进儿童深度参与的核心问题;二是在课堂教学活动中由学生所提出的,涉及学科课程主题实质的重要问题。前者意味着教师要把实质性的学科内容“教法化”——让学科实质能够被学生触及并逐步理解掌握,后者意味着在充满不确定性的课堂师生互动中,教师要能够及时抓住学生的那些反映数学学科思想实质的朴素想法并加以拓展。
问题驱动式教学意指教师通过精心规划数学教学任务,设计以学科内容本质和儿童认知特质为两翼的课程核心问题,引导学生开展数学学习活动,让学生利用必要的课程资源,通过自主、合作、探究学习获得知识建构和能力提升,它应当是一种较大限度地促进学生优质化发展的相对稳定的教学策略。
我们试图通过实践应用的积累,自下而上构建起一种关注学科内容本质和儿童认知特质的教学设计策略,以期为小学数学课程改革提供一种具有现实意义的实践样本,为小学数学课程教学改革做出切实而属己的贡献,努力实现“三个走向”。
第一,从“理论”走向“实践”。努力使得教育理念不仅仅是停留于观念层面,还要变成一线教师愿意去尝试和实践的教学设计思想和策略,能够为教师的实践提供可供参考的范例。
第二,从“中学”走向“小学”。在研究成果的同时,深入思考小学数学教学的实践过程,关注儿童的身心特点和认知规律,较为全面和系统地进行理性思辨,明晰并提炼问题驱动式小学数学教学的价值、意义、特点和方法等。
第三,从“批判”走向“建设”。教师对教学内容的本质把握不够,教学中的关键性问题设计失当,往往会造成课堂教学在设计和实施的过程中遭到各方批判。问题驱动式教学试图以驱动式问题为突破,优化教学设计,净化教学流程,着力追寻一种“生动且深刻”“简约而不简单”的教学境界。
三、课改背景下的教学思考
佐藤学认为,课程改革的基本方向就是要让教学从“计划(program)型”变为“课题(project)型”,从“爬楼梯型”转变为“登山型”。“爬楼梯型”属于传统的课程形式,定下目标,分步切块实施,最终达到目标。“登山型”则以主题为中心,然后向“中心”攀登,在这个过程中会发现很多种上山的途径,也就是很多种获得知识的方法。问题驱动式数学教学就是要引领数学教学逐步由“爬楼梯型”走向“登山型”,起步的时候即使不是“登山型”,也应该从“爬山坡”开始,逐步走向“登山”,实现从“计划型”到“课题型”的教学转变。
谈数学课程改革,不能不提数学课程标准,它是指导我国数学课程改革的纲领性文件,任何数学教学改革都应该与课程标准保持内在的一致性,这种一致性更强调内在的、理念上的一致性,而不能停留在形式层面。用最简洁的语言概括2011版数学课程标准的修订要点,就是“三个‘进一步’”:进一步突出数学性,进一步强调儿童性,进一步重视过程性。这“三个‘进一步’”在问题驱动式小学数学教学中都得到了较好的关注。
第一,进一步突出数学性。现代学习理论研究表明,组织良好的知识不是对相关领域的事实和公式的罗列,它应该是围绕“核心概念”或“大观念”组织的。问题驱动式教学就是抓住核心问题组织教学活动,这里的核心问题往往就是从核心概念、大观念出发的,而紧扣核心问题展开的教学活动才能让学生的知识结构围绕核心概念来组织,这种有序的结构,能够让学生在收获更多知识的同时,收获良好的、优化的知识结构。学科的基本观念或者核心概念如同“源头活水”,学生头脑中有这样的“源头活水”,在内外因素的交互作用下,就能源源不断地流淌出各种知识形态,由此生成的知识,更便于应用,更易于记忆。对于知识掌握,重要的是知识的序列和结构,因为有结构的知识才可能成为有活力的知识,才可能成为创新型的“活知识”。
第二,进一步强调儿童性。美国国家研究委员会在《人人关心数学教育的未来》的报告中指出:没有一个人能教数学,好的教师不是在教数学,而是激发学生自己去学数学……只有当学生通过自己的思考建立起自己的数学理解力时才能真正学好数学。基于此,问题驱动式数学教学强调:从儿童出发,从儿童已有的知识经验出发,关注儿童主体性的充分发挥,引导儿童自己学数学、从自己的实际出发去建构属于自己的数学;教学规划要符合儿童的年龄特征,能够调动儿童的学习内驱力,让儿童在接受教育的过程中享受这个过程,变“要我学”为“我要学”。教学中,教要“到位”,但不能“越位”。教师教学的过程就是引导学生生疑、质疑、解惑的循环往复的过程,是启发学生思考、探究、发现、创造的过程,是促使学生想学、乐学、会学、学会的过程,归根到底就是“让学习真正发生”。
第三,进一步重视过程性。人本主义的倡导者罗杰斯认为,真正能够影响一个人的行为的知识,只能是他自己经历的知识。从这个角度看,只有教学的过程充分展开了,整个的数学教育才可能成为我们所想要的,才可能真正从“双基”走向“四基”,从“两能”走向“四能”。人们曾经认为“过程”没有价值,后来意识到,只有重视“过程”,才能够帮助受教育者更好地掌握知识与技能。问题驱动式教学就将“过程”本身作为一个重要的教学目标,经历“过程”不仅仅是为了获得知识与技能,“过程”本身所蕴含的价值也应纳入教学目标的范畴。我们以为对于学习者而言,“结果”的价值主要在于它的消费价值和使用价值,而“过程”的价值主要在于它所具有的“生产性”或“发展性”,但从某种意义上看,“过程”比“结果”更有价值。
四、基于团队立场的教学展望
为了更好地开展研究,我们组建了完整的问题驱动式教学研究团队:一是以学校“未名教育家”教师发展梯队和“问题驱动式教学”工作室为主体的核心团队,大家以“主张”为抓手,在“主张”上作相对专业的深度思考,关注问题驱动式教学的现实价值追问、理论基础梳理、意义内涵解析、典型案例剖析、教学实施原则、教学范式建构等;二是全校数学教师团队,以数学教研组为单位展开对话题的探索,全校六个年级数学教研组每年都提出自己感兴趣的研究话题。(2016学年的研究话题如下表所示)
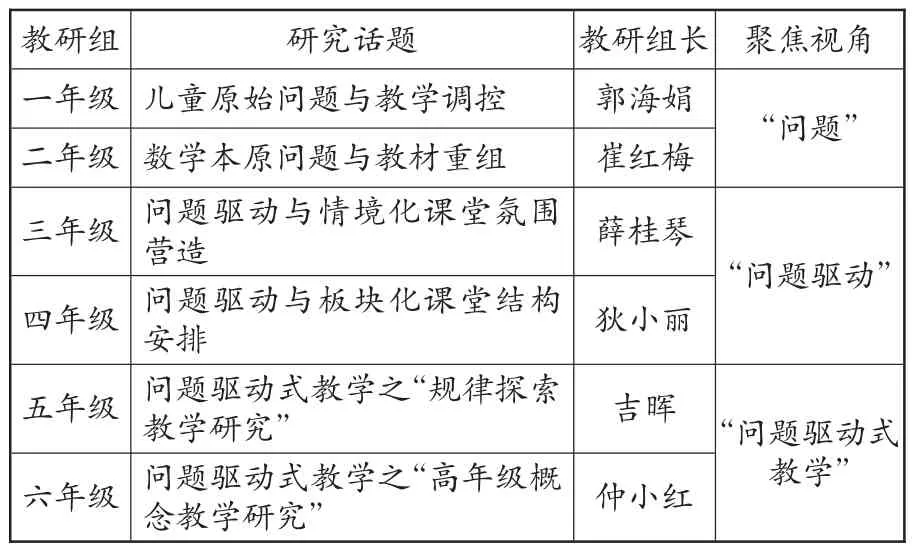
教研组 研究话题 教研组长 聚焦视角一年级儿童原始问题与教学调控 郭海娟 “问题”二年级数学本原问题与教材重组 崔红梅三年级问题驱动与情境化课堂氛围营造 薛桂琴四年级问题驱动与板块化课堂结构安排 狄小丽“问题驱动”五年级问题驱动式教学之“规律探索教学研究” 吉晖“问题驱动式六年级问题驱动式教学之“高年级概念教学研究” 仲小红 教学”
这样,每一位数学教师都在这一话题的观照下找到了自己的研究视角,找到了自己的“可为之处”,开展了基于自身实践的教学探索。我们在“问题驱动式教学”上进行思考与探索已经有四年多,在这四年里,整个团队都获得了快速的成长:荣获“南通市优秀教研组”“南通市优秀教师群体”等荣誉称号,团队成员参加全国信息技术与学科整合优课评比获得一等奖,省、市级网络团队教研比赛均获得小学数学组一等奖第一名,在省级以上报刊发表文章一百多篇,十多名成员先后被评为市、县级学科带头人。2015年1月南通市教育局名师培养导师团和海安县教育局联合举办的“南通市名师培养对象储冬生团队展示研讨活动”,获得广泛好评。
随着团队研究的深入,我们的思考也逐渐深入。前不久工作室成员苏兴进老师在一篇论文中谈到他关于问题驱动式教学的最新思考:
“当数学能和儿童生活发生意义关联,当问题能以儿童接受的方式加以呈现,问题就有了驱动价值——教学板块分层推进,数学学习就自然发生了!推动这一切的正是基于学科本质的‘核心问题’与‘一般问题’的巧妙‘配合’。问题驱动可以让静态的知识文本动态呈现,能够与儿童有效对话;问题驱动可以让学生的思考从‘被动接受、杂乱无序’变成‘主动创造、开放有序’;问题驱动可以让学生的合作从形式走向实质。问题驱动让课堂逐渐从‘以教师为中心,讲授为主’,转向‘以学生为中心,探究为主’。”
展望未来,前行的道路上一定还会有新的挑战。正如一位美国学者所说的那样,我们数学教师会面临两个重大的难题:第一,我们几乎完全不知道人是如何处理数学问题的;第二,我们几乎完全不知道人是如何学习数学的。甚至是那些每天用大部分时间来思考数学的数学家,我们也无法想象在解决数学问题的时候他们的头脑中到底发生了什么。一个问题在前一秒钟还看似很棘手,而后一秒钟答案变得显而易见了,一切就像出现了奇迹一样。这便导致了我们的数学教学在很大程度上仍然是一门艺术——需要好教师,依赖传统、直觉、经验以及从别的教师那里汲取的“智慧”——而不是一种基于确凿科学理论和证据的实践。我们深知前行的艰难,但我们仍对后续的研究充满信心,因为我们坚信“教育是极其复杂的事情,每个人均有可为之处。”(顾明远语)
综上,只有努力尝试建构问题驱动式教学模式,才可能让我们的教学研究更深入,让我们的共同体建设更具实质,让我们的学科教学更有区域特质,让我们的数学教育进一步逼近教育的内核。但是,我们必须时刻警醒,不能走入“模式化”的误区,虽然我们有共同的追求,但是我们每一个人更应该有自己个性化的建构。问题驱动式教学最终追求的应该是“和而不同”,是“各美其美,美人之美,美美与共”的共生境界。
(责编金铃)
[中图分类号]G623.5
[文献标识码]A
[文章编号]1007-9068(2016)05-001

