水电站厂内经济运行实用化方法研究

文 丹

（大连金州新区水利管理服务中心，辽宁大连116100）



水电站厂内经济运行实用化方法研究

文 丹

（大连金州新区水利管理服务中心，辽宁大连116100）

摘要：大容量巨型水电站普遍具有高坝、高水头、高负荷的运行特征，给电网安全带来隐患。本文从调度工作出发，在满足机组运行安全的前提下，探讨一种实用化的水电站厂内经济分配方法。分析结果表明，该方法能够有效满足调度人员工作需求，是一种切实可行的负荷分配方法。

关键词：厂内经济运行；机组；安全；优化调度

1　引言

伴随电网的快速发展，我国已经成为世界上电力装机容量、发电量及电网规模最大的国家。据中电联公布的2014年电力运行简况［1］，截止2014年底，我国电网装机已达到135973万kW，其中，火电占总装机的绝大部分，大约67.3%，水电大约占总装机的22.2%。水电已成为仅次于火电的第二大电源，同时也是最主要的可再生能源。水电以其蕴藏规模大、开发和运行技术成熟、启停灵活且响应迅速等特点得到前所未有的快速发展，在电力供应中发挥了不可替代的重要作用［2］。然而，水电系统规模快速扩大带来巨大经济效益的同时，也给电网调度带来的新的挑战，特别是近些年投产的大容量巨型电站，如红水河的龙滩电站坝高216.5m，水头150m左右，装机49OOMW，澜沧江的小湾电站坝高294.5m，水头25Om左右，装机420OMW等。这些电站普遍具有高坝、高水头、高负荷的运行特点，运行平稳性相对较差，给电站和电网安全带来了严重的安全隐患。调度员在日常调度工作中，必须考虑电站的运行安全，开展实用化厂内经济运行方法具有重要意义。

水电站厂内经济运行［3］是指在优先满足安全、可靠的基本前提下，通过对电厂发电设备的合理安排，以期达到最优的发电方案，合理配置资源，减少损失并获得最大的经济效益。实际运行中，即在已知电网调度给定的日负荷过程的前提下，寻求电站机组消耗水量最小的负荷分配方案。常见的求解方法有：动态规划法、遗传算法和等微增率法等［4-6］。

本文根据电站机组的实际运行特性，提出了一种实用化的水电站厂内经济分配方法。该方法采用动态规划进行求解，并结合数据库存储及Java编程语言编码实现，在满足机组运行安全、电站各类约束条件下，寻求最经济的负荷分配方法。以国内某大容量巨型电站某日96点负荷分配过程为例，仿真结果能有效满足日常调度需求，验证了该方法的有效性和实用性。

2　算法简介

2.1 水电常用优化准则

（1）以水定电的优化准则。已知电站的发电流量或者入库流量，目标为电站机组出力最大，以获得最大的发电量。

（2）以电定水的优化准则。此原则只针对有调节能力的水电站而言，是指已知电网调度部门给定的电站负荷，目标为尽量减少消耗的发电水量，以获得最经济的发电方式。

2.2 DP算法描述

动态规划算法［7，8］（简称DP）是解决多阶段决策过程最优化问题的常见方法之一，最早由美国数学家贝尔曼在1951年提出，并于1957年发表了该原理的著作。其核心思想是通过对复杂的多阶段问题进行“离散”，将其细分为多个子阶段，然后逐段求解，通过状态的不断变换，最终获得最优的决策序列。目前已经广泛应用于许多科学领域，例如军事、生物、工程、经济、管理等，取得了令人满意的效果。一般地，动态规划算法包含以下几个步骤［9，10］：

（1）阶段

将待求解的多阶段决策问题按照一定的原则划分为多个子阶段，划分原则要根据实际求解问题的性质来确定，可以是空间特征，例如电站水位、发电流量等，也可以是时间顺序。一般用k表示，即1，2，3，…，k，…，n。

（2）状态

状态是描述事物当前特征的量，既可以是空间的某个位置，也可以是时间上的某个时刻。动态规划算法设计中，状态的选取必须要满足“无后效性”。所谓的“无后效性”，又称马尔柯夫性，是指后一阶段事物的发展，仅于目前现阶段的状态和所做的决策有关，而与前阶段或历史阶段的状态和决策无关。常见的描述有状态变量sk（statevariab1e）和状态集合Sk（setofadmissib1estates）。

（3）决策

决策，顾名思义，就是所选择的策略。当某阶段的状态已经确定，他下一阶段状态是未知的，存在多种选择。此时，决策者选中某一选择，那么事物将从当前状态，根据选择的策略，演变到下一状态。常见的描述有决策变量uk（sk）（decision variab1e）和决策集合Dk（sk）（setofadmissib1edecision）。

（4）策略

综合各个阶段的决策，形成一组有序的决策序列，即为策略。

（5）状态转移方程

按照步骤2和3中所描述，假设系统目前处于k阶段，此时的状态记作Sk，假设下一阶段，即K+1阶段的状态记作Sk+1。由于状态选择的无后效性，k阶段到K+1阶段状态的演变（也称作转移），仅由k阶段的决策uk（sk）决定。可用以下数学公式表示：

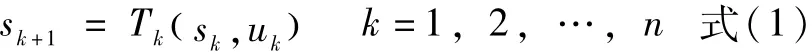
（6）指标函数

当决策者做出某个决策之后，自然想知道该决策的效果或者优劣程度，以选择最优的决策。指标函数就是用来评价和衡量决策优劣程度的一种确定性的数量函数。指标函数的选择需根据实际问题的目标而确定，例如耗水量、利润等。一般用vk（sk，uk）表示。

2.3 算法设计

（1）目标函数

一般地，电站的机组台数是固定的，不考虑机组动态投产的影响，给定的电站负荷下，在已选定的固定机组之间的进行负荷的最优分配。设电厂总负荷为N，选定某n台机组共同完成这一生产任务，那么如何在这n台机组之间负荷分配N，以使全厂总工作流量最小，这是一个空间最优化问题。如果考虑电站某日实际负荷过程，运用动态规划进行各个时段负荷分配，同时考虑各个时段时间的相互影响，即是一个时间最优化问题。

经分析，其最优化数学模型为：

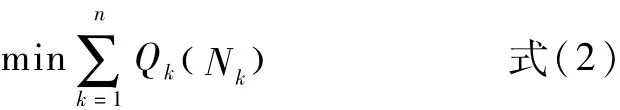
其中，为号机组当出力为时的发电流量；为第k号机组的出力；为电站参加发电的机组台数。

（2）约束条件

①水量平衡约束

式中：Vt为水电站在时段t的库容，单位：m3；Qt=Qn，t+QT，t为水电站在时段t的入库流量，单位：m3/s；Qn，t为水电站在时段t的区间流量，单位：m3/s；QT，t为考虑水流滞时后上游水电站流入该电站时段t的总流量，包括发电流量和弃水流量，单位：m3/s；Q1，t、qt分别表示水电站在时段t的弃水流量和发电流量，单位：m3/s；Δt为t时段小时数。

②出力上下限约束

为k号机组在时段t的出力下限，单位：MW。

③发电流量约束

④库水位约束

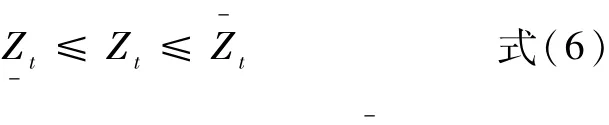
式中：Zt为水电站在t时段水位，Zt、Z-t为其水位的其上下限，单位：m。

⑤出力爬坡限制

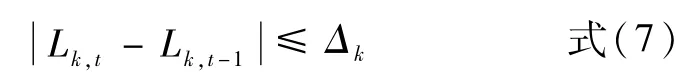
式中：Δk为机组k在相邻时段间的最大的出力波动值，单位：MW。

⑥开停机最小持续时段数要求

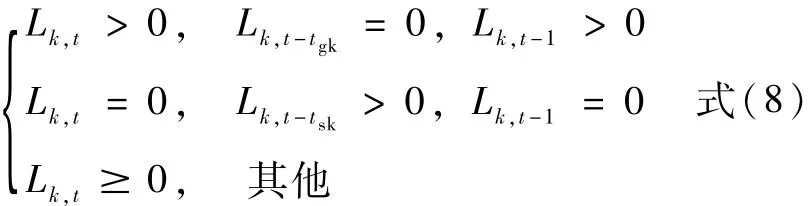
式中：tgk为机组k最小开机数，tsk为机组k的停机持续时段数。

⑦机组出力波动控制约束

式中：tv为一轮出力升降过程中最高或最低点需持续的最少时段数。

⑧振动区约束：

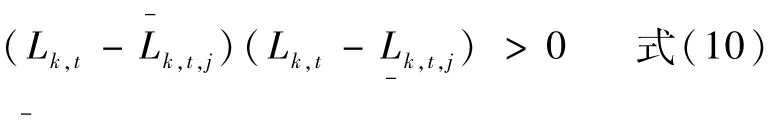
式中：Lk，t，j、L-k，t，j分别为机组k在t时段的第j个振动区的上限与下限。

（3）算法编程

文中采用动态规划方法求解上述的固定机组之间的负荷最优化问题，并以JAVA程序语言进行编程，其顺向递推方程为：

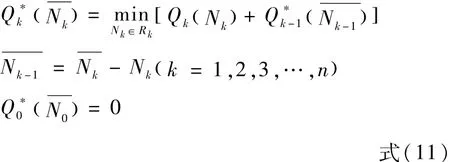
程序中的变量说明如下：

k—机组台号及台数，k =1，2，…，n；

N（k）—第k号机组容量；

Ns—电厂装机容量；

Nk—1～k号机组的总容量；

Nk1—1～k-1号机组的总容量；

j—状态变量，发电任务；

i—决策变量，k号机组的出力；

Q（k，i）—第k号机组决策变量为i，即出力为i时的发电流量；

Q1（j）—1～k号机组的总工作流量；

Q2（j）—1～k-1号机组的总工作流量；

X，Y—用于比较的中间变量；

I0—用于计算过程中存放相对交友决策i的中间单元；

N0（j，K）—存放优化负荷分配结果。其含义是：当电站所承担的总负荷为J时，如果用k台机组去分配，第k号机组所需要承担的负荷。顺向递推方程组：

采用逆向求解，即可得到机组最优负荷分配表

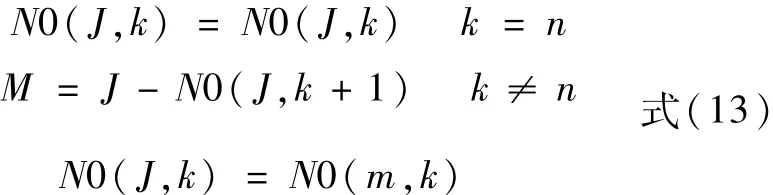
综上，利用上述顺向递推方程组和逆向求解机组最优负荷分配程序，即可获得电站机组最优负荷分配表。需要注意的是，以上所讨论的是固定机组之间的负荷优化分配问题，在实际工程中，往往已知的是电站的实际负荷，需要先选取机组台数、台号并在选定的机组之间优化分配负荷。在编程时，认为机组负荷为零时意味着机组停机，此时不消耗流量，在流量特性曲线中，需将出力为零时的流量设置为零。

3　工程应用

为了验证文中所提方法的可行性与有效性，以国内某典型的大容量巨型电站为例，已知其某日96点负荷过程，并在其包含的各机组之间进行安全经济分配。

3.1 电站概况

该水电站属于年调节水库，坝址控制面积9.85万km2，坝址处多年平均流量1630m3/s，年径流量514亿m3。该电站正常高水位375m，死水位330m，正常高水位库容162.1亿m3，保证出力为1234MW。电站共有7台机组，每台机组的铭牌出力都为700MW，最大过流能力为710m3/s。

3.2 电站机组流量特性曲线

水电站的NHQ信息以数据库形式保存，在实际运用中可根据这些信息，按实时时段的不同水位，插值得到不同水位下的NHQ信息。显然，不同的水位下，有不同的机组运行NHQ信息。不仅如此，不同水位下，机组可运行的安全区域也是不同的。定义：

表1　电站汛期信息

机组的安全运行区间为：{机组稳定运行区} U{机组过渡区}；

机组的非安全运行区为：{汽蚀与振动区} U{机组涡带区} U{机组粗糙运行区}。

根据不同的电站水头，机组的的安全运行区和非安全运行区数据如下表2中所示。该数值根据稳定性试验结果及机组综合特性曲线分析得到。

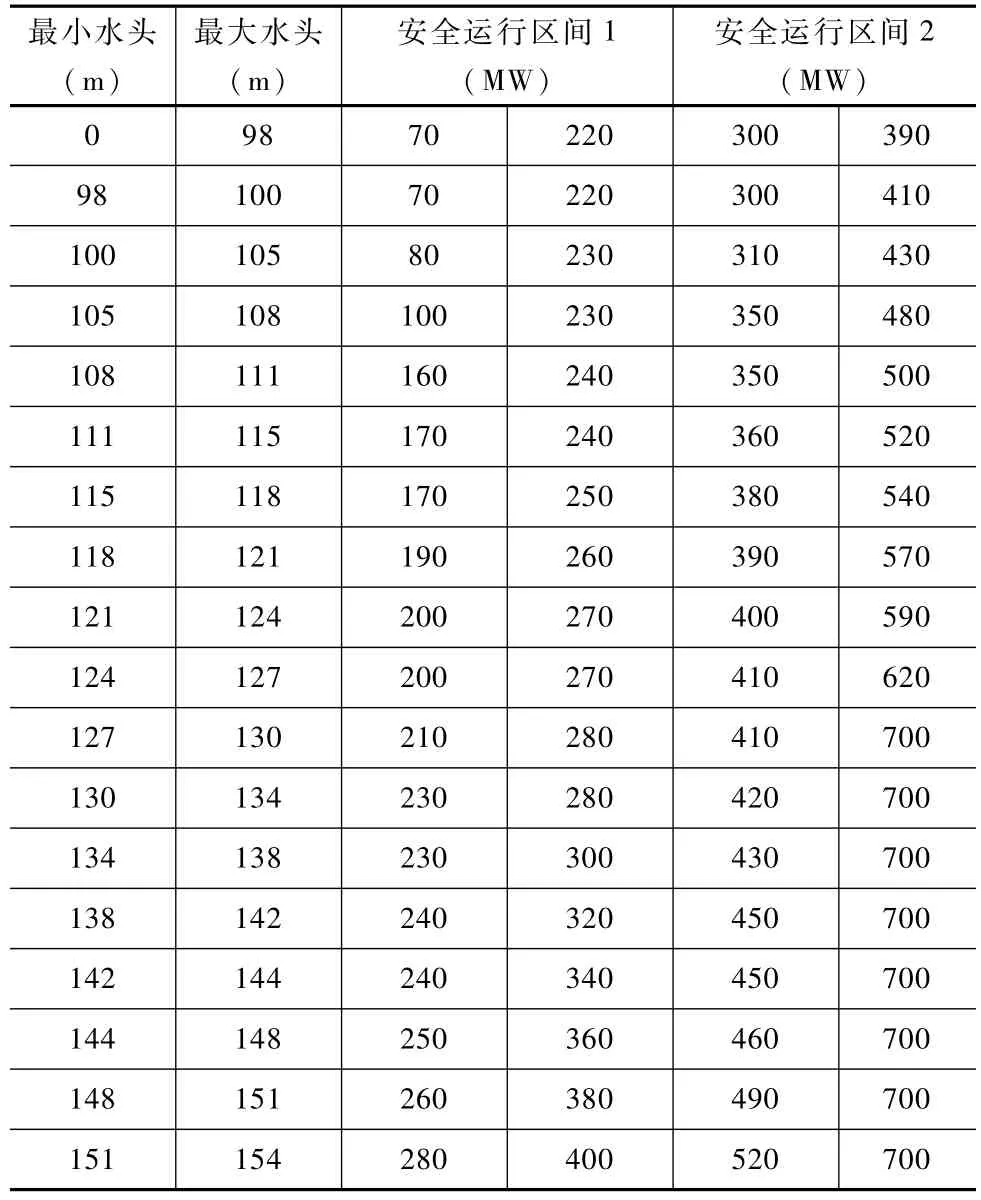
表2　机组在不同水位下的安全运行区间

3.3 模型求解

按照以上描述的目标及约束条件，本文采用动态规划算法进行求解所采取的基本思路如下。

（1）检查基础数据是否完整，并校核数据的准确性；

（2）根据已知的电站机组流量特性NHQ信息，运用动态规划算法求解出在不同机组组合、不同水位、不同负荷下的最优工作流量和各个机组之间的最优负荷分配，得到最优负荷分配表，并将其存入orac1e数据库中；

（3）已知某日负荷过程如下图1所示，即可得到不同时段负荷，根据这个负荷和对应时段的水位，即可在最优负荷分配表中插值得到最优工作流量和最优机组组合，以此类推，得到全天所有时段的厂内经济运行结果。

4　结语

本文对水电站厂内经济运行的动态规划算法数学模型以及计算机求解进行了研究和改进。根据算法的基本原理和操作步骤，阐述了算法模型在水电站厂内经济运行的具体实现过程，并利用Java编程，结合orac1e数据库存储技术，编制了水电站厂内经济运行的动态规划程序。将编制的程序应用于国内某大型水电站实际日负荷分配过程，结果表明该方法能够得到最优解，并满足机组安全运行要求，证明了该方法的有效性和实用性。但随着机组台数和算法离散份数的增加，计算时间将会大幅增加，如何提高求解效率是值得进一步深入研究的。

参考文献

［1］中电联公布2014年电力工业运行简况［EB/OL］.httP：//www. hydroPower.org.cn/showNewsDetai1.asP？nsId =15566.

［2］全国水利资源复查工作领导小组.中华人民共和国水力资源复查成果（2003年）总报告［M］.中国电力出版社，2004.

［3］张勇传.水电站经济运行原理［M］.北京：水利电力出版社，1981.

［4］刘博，周建中，杨敬涛.基于动态规划和遗传算法的混合算法研究［J］.计算机仿真，2004（12）.

［5］姚齐国，张士军，蒋传文，权先璋.动态规划法在水电站厂内经济运行中的应用［J］.水电能源科学，2005（02）.

［6］向凌，杨敬涛，周建中，周泰斌.动态规划法和遗传算法在清江工程项目中的实际比较［J］.水力发电，2003（09）.

［7］周之豪，施熙灿等.水利水能规划［M］.北京：中国水利水电出版社，1997.

［8］唐焕文，秦学志.实用最优化方法［M］.大连：大连理工大学出版社，1994.

［9］陈森林.水电站水库运行与调度［M］.北京：中国电力出版社，2008.

［10］董子敖.水库群调度与规划的优化理论和应用［M］.山东：山东科学技术出版社，1989.

作者简介：文 丹（1981年—），女，工程师。

收稿日期：2015-10-16

DOI：10.3969 /j.issn.1672-2469.2016.03.030

中图分类号：TV737

文献标识码：B

文章编号：1672-2469（2016）03-0082-04