基于扰动转矩反馈的机械谐振抑制方法
咸明辉,罗欣,沈安文,刘峰(华中科技大学自动化学院,湖北武汉430074)
基于扰动转矩反馈的机械谐振抑制方法
咸明辉,罗欣,沈安文,刘峰
(华中科技大学自动化学院,湖北武汉430074)
摘要:伺服驱动被用在很多工业应用中,伺服系统中电机和负载之间的柔性连接环节会恶化伺服系统的性能,甚至会引起系统不稳定。分析了伺服系统产生机械谐振的原理,并提出了一种基于扰动转矩反馈的谐振抑制方法。该方法利用Luenberger观测器来观测扰动转矩,并将扰动转矩通过一个比例积分环节反馈回电流给定。此外,还给出了一种反馈系数K的整定方法,并在理论上分析了该参数整定方法的合理性。最后,基于Matlab/Simulink平台搭建了伺服谐振系统的仿真模型,并对提出的方法进行了仿真验证。
关键词:伺服系统;谐振抑制;扰动转矩反馈;Luenberger观测器
交流伺服驱动被应用在很多工业领域中,例如金属切割,包装,纺织业,web处理,自动装配和印刷等[1]。在实际工业应用中,执行机构通过联轴器、传动轴等传动装置与电机相连。这些传动环节的刚性限度往往是有限的,但是在进行控制器设计的时候,设计者一般都是将连接环节当成是理想刚性环节来处理[2]。这种简化的处理会恶化系统的性能,甚至会使系统出现不稳定。
近年来,很多学者都致力于伺服谐振问题的研究,他们提出了很多抑制谐振的方法。其中最直接的方法就是降低系统在谐振频率处的增益。在系统中加入滤波器来抑制谐振是比较常用的方法[1]。在使用滤波器抑制谐振的方法中,最简单的就是使用低通滤波器来降低系统的整体增益,使得系统在谐振频率处获得足够的稳定裕度,但是使用低通滤波器会降低系统的带宽,导致系统性能下降。第2种方法就是在系统中加入陷波器,陷波器类似于一个带阻滤波器。陷波器可以在某个特定的频率范围内提供很大的幅值衰减,在谐振系统中加入陷波器可以有效衰减谐振频率附近的幅值增益,同时对其他频率处产生较小的影响。因此基于陷波器的谐振抑制方法在实际中被广泛应用。还有一种滤波器是双二阶滤波器,它可以完全消除谐振方程带来的影响,在理论上是最可行的办法,但是,它对参数的估计要求非常高,而且在负载侧会存在振荡[1],在实际中较少用到。
除了滤波法之外,抑制谐振的另外一种有效方法是加速度反馈法[3]。加速度反馈的本质是通过改变系统的电机负载惯量比来抑制谐振。但是,在实际的伺服系统中,直接对位置信号进行微分得到的加速度是不可靠的,因为位置信号的获取存在量化误差而且会引进外界的噪声,如果直接位置信号进行微分会引入更大的噪声和误差,而且还会带来相位滞后,恶化系统性能。另一种获得加速度的方法就是在系统中安装加速度传感器,但是这样会增加系统的成本同时会减小系统的稳定性。因此,为了获得精确的加速度信号同时又不影响系统的稳定性,可以用观测器来代替传感器[4],常用的观测器为Luenberger观测器。
Luenberger观测器除了可以观测系统的加速度外还可以观测电机的扰动转矩。本文通过Luenberger观测器来观测扰动转矩,并将其通过一个比例积分环节反馈到电流给定,这种方法改变了系统的等效谐振方程,进而达到抑制谐振的目的。从仿真结果可以看到,通过本文提出的方法,系统电机侧和负载侧的谐振均得到了较好的抑制。
1 机械谐振原理
在实际工业应用中,执行机构例如联轴器、传动轴等传动装置的刚性限度是有限的。如果忽略传动装置的惯量,可以将传动装置等效看作一个弹性系数为Ks,阻尼系数为Kw的弹性装置,从而整个系统可以近似等效成为一个二质量系统[5]。如图1所示。
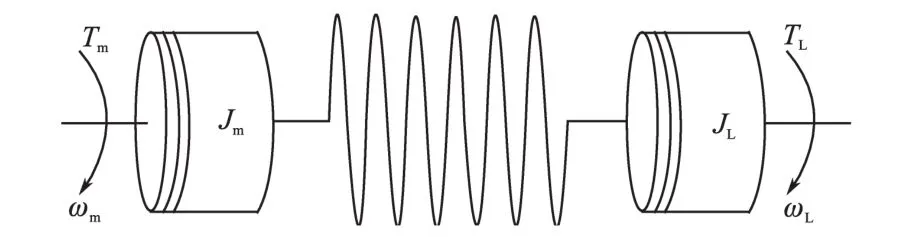
图1 等效二质量模型Fig.1 Model of two-inertia system
由电机侧运动方程可得:
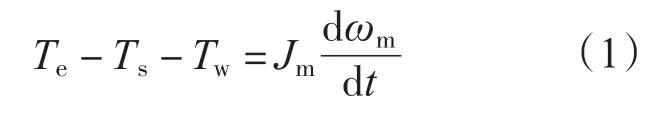
由传动轴的受力方程可得:
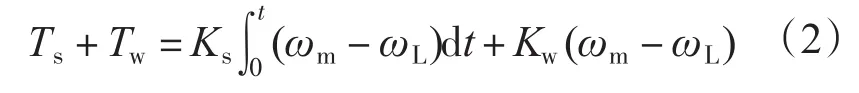
由负载侧的运行方程可得:
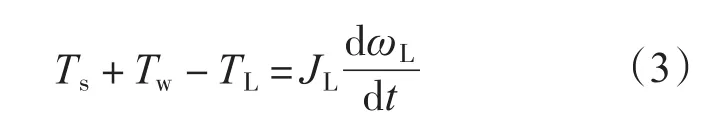
式中:Te为电磁转矩;Ts为传动轴产生的弹性扭矩;Tw为传动轴产生的阻尼力矩;Ks为传动轴的等效弹性系数;Kw为传动轴的等效阻尼系数;Jm,JL分别为电机侧和负载侧的惯量;ωm,ωL分别为电机侧和负载侧的速度。
根据系统的时域微分方程式(1)~式(3)可以得到系统的频域传递函数框图如图2所示。
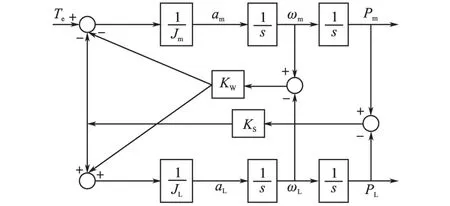
图2 柔性环节传递函数框图Fig.2 Block diagram of compliant link
根据图2的柔性环节传递框图可以得到电磁转矩Te到电机侧速度ωm的传递函数为
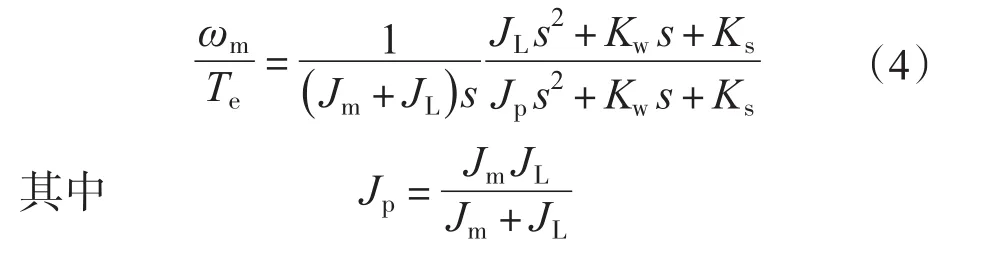
与理想刚性系统相比,柔性环节在刚性环节的基础上增加了一个双二阶项,这个双二阶项被称为谐振方程。通常情况下,传动轴的等效阻尼Kw都很小,如果忽略系统的阻尼,谐振方程的分子在频率fares处取得极小值,分母在频率fres处取得极小值,fres和fares分别被称为谐振频率和反谐振频率[6],其表达式如下:
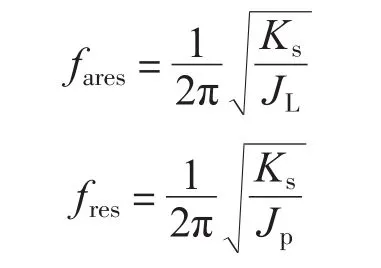
图3为经典的电机速度控制框图。
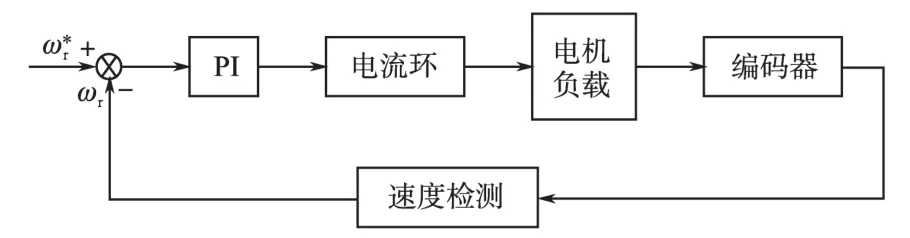
图3 电机速度控制框图Fig.3 Block diagram of motor speed control
由图3所示的控制系统框图可以得到理想刚性系统,柔性系统,以及柔性环节的Bode图如图4所示。
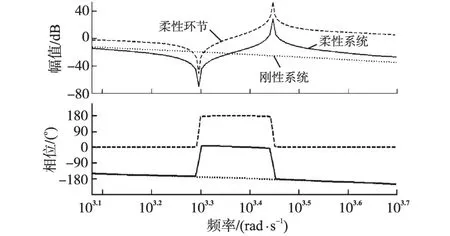
图4 刚性系统以及柔性系统Bode图Fig.4 Bode diagram of rigid and compliant system
由图4可以看出理想刚性系统在系统相位穿越180°时,幅值裕度大于0,系统是稳定的。对于柔性连接系统,由于叠加了柔性环节的影响,系统在谐振频率附近的幅值增益快速增大,导致系统在穿越180°的时候系统的幅值裕度小于0,这会导致系统出现不稳定。
2 基于扰动转矩反馈的谐振抑制方法
谐振抑制的直接途径就是改变谐振方程对系统带来的影响,本文通过Luenberger观测器观测扰动转矩,并将扰动转矩通过一个比例积分环节反馈回电流环给定,从而等效改变系统的谐振方程,达到抑制谐振的目的。加入反馈后系统的原理图如图5所示。
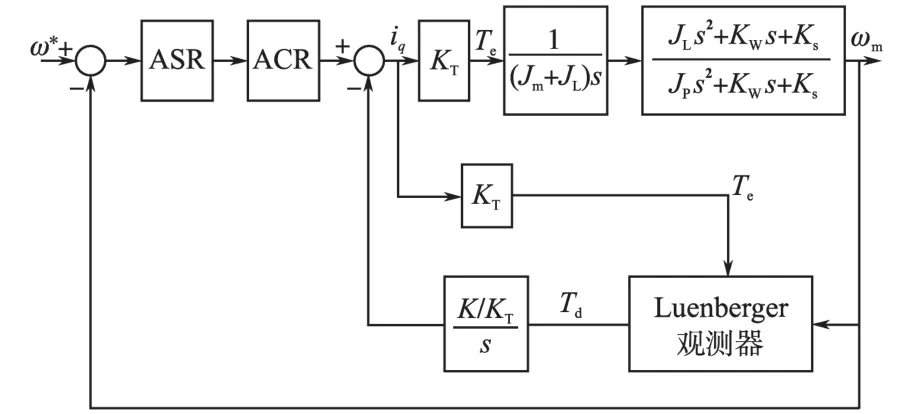
图5 基于扰动转矩反馈的谐振抑制原理图Fig.5 Resonance suppression based on disturbance torque feedback
Luenberger观测器的结构图如图6所示。
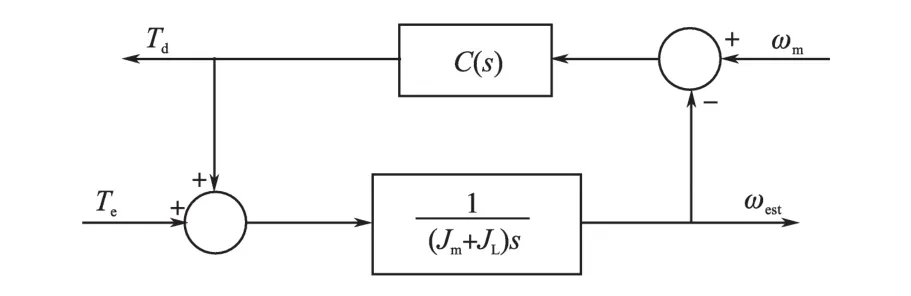
图6 Luenberger观测器结构框图Fig.6 Block diagram of Luenberger observer
图6中Luenberger观测器的补偿器为PID补偿器,补偿器的表达式为
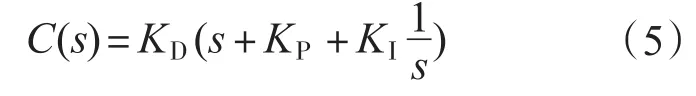
设由Luenberger观测器观测出的速度为ωest,系统电机侧的实际速度为ωm,扰动转矩为Td,根据Luenberger观测器的原理有:
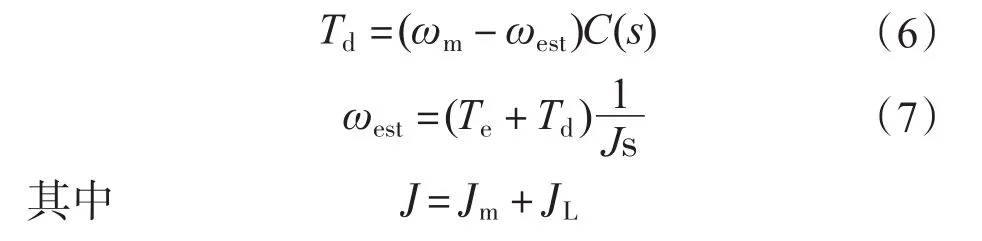
将式(7)的ωest表达式带入式(6)中,得到扰动转矩Td表达式:
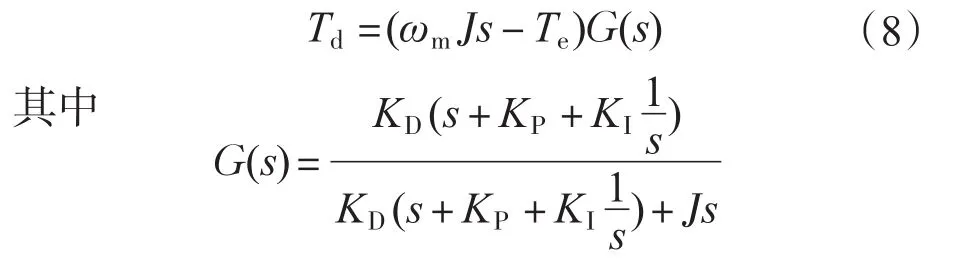
由G(s)的表达式可以看出,G(s)本质上是1个低通滤波器。而且,在Luenberger观测器参数整定的时候一般有KD远大于J,因此,可以忽略G(s)分母中的Js项,此时有

此时,式(8)可以简化为
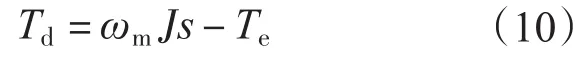
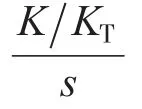
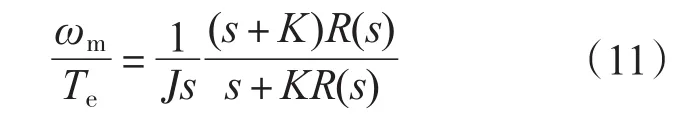
其中R(s)为谐振方程:
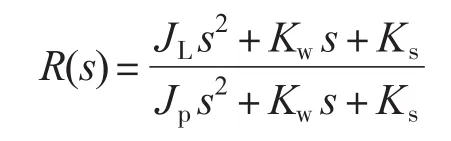
将式(11)进一步展开得到
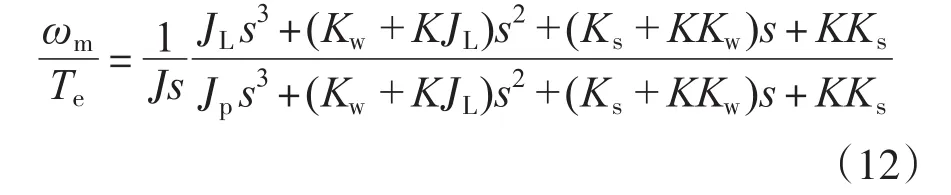
由式可以得到,经过反馈之后系统的等效谐振方程变为
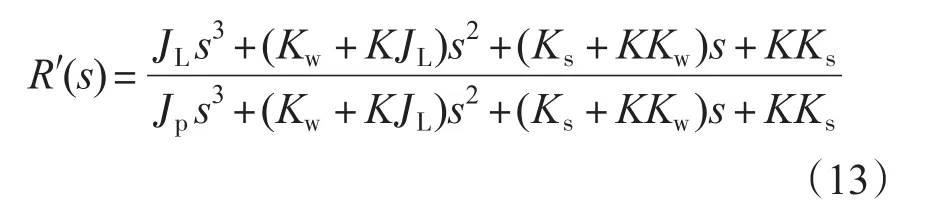
画出引入反馈之前的谐振方程R(s)和引入反馈之后的等效谐振方程R′(s)的Bode图如图7所示。
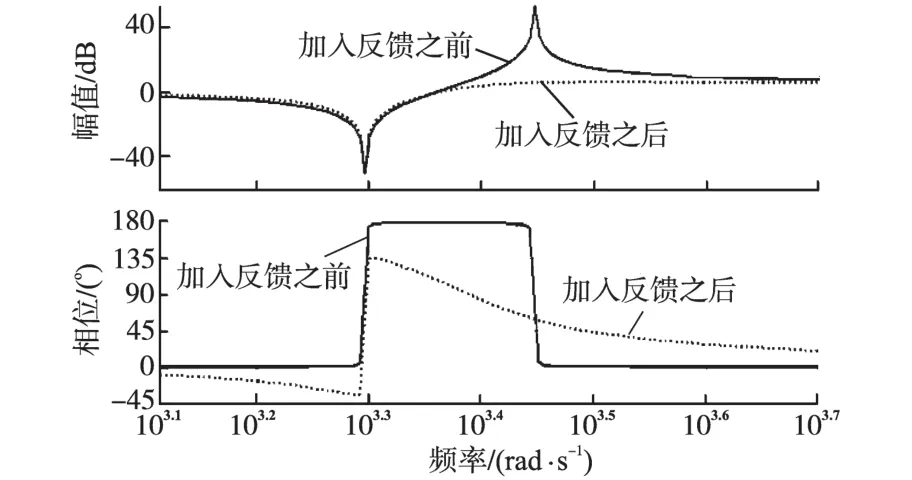
图7 加入反馈前后谐振方程Bode图Fig.7 Bode diagram of original resonance equation and resonance equation with proposed feedback
由图7看出,引入反馈之后系统的等效谐振方程在谐振频率处的幅值增益大幅减小。图8为加入反馈之后整个系统的开环Bode图。
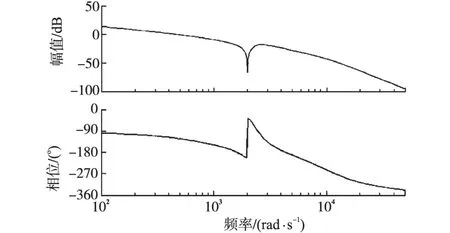
图8 加入反馈后系统等效Bode图Fig.8 Bode diagram of system with proposed feedback
由图8可以看出,加入反馈之后,系统的相频曲线穿越-180°时,幅值裕度大于0,表明系统是稳定的,不会发生振荡。
3 反馈系数K的整定
虽然扰动转矩反馈在谐振频率处衰减了系统的幅值增益,但同时给系统带来了一定的相位滞后,如图9所示。
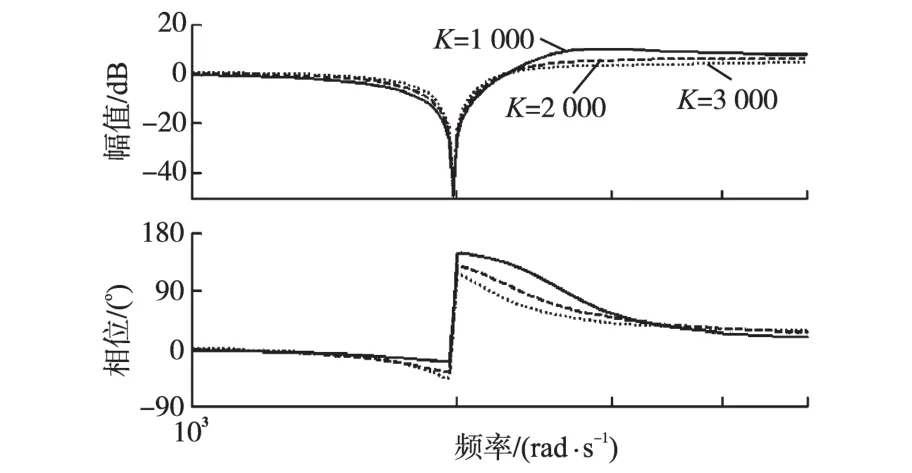
图9 K=1 000,2 000,3 000时系统等效谐振方程Bode图Fig.9 Bode diagram of equivalent resonance equation,where K=1 000,2 000,3 000
由图9可以看到,虽然K越大,R′(s)在谐振频率处衰减的幅度越大,但是随着K的增大,R′(s)在低频处产生的相位滞后也越来越大,这个相位滞后会减小系统的开环带宽,影响系统性能。所以K不能无限制加大。
由谐振方程R(s)和R′(s)可以得到,当s趋近于无穷的时候,其增益都趋近于1个恒定值KR。
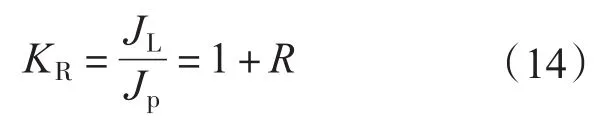
式中:R为系统的负载和电机的惯量比,R=JL/Jm反馈K值求解示意图见图10。
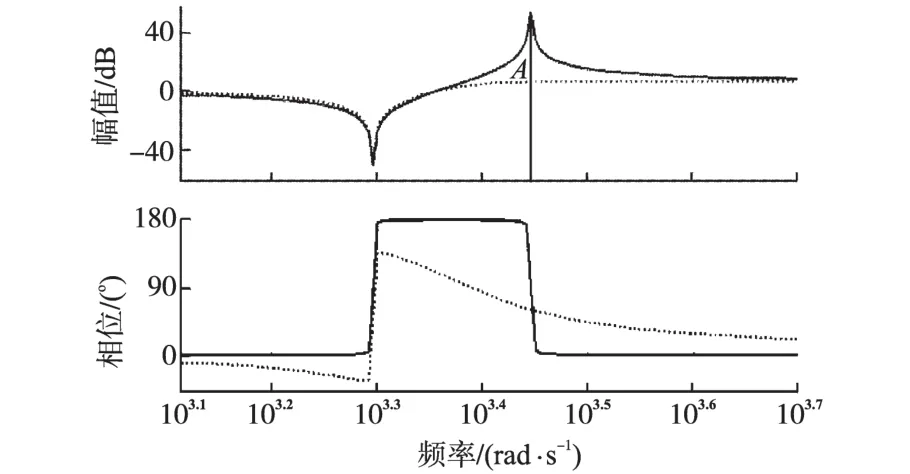
图10 反馈K值求解示意图Fig.10 Feedback coefficient calculation diagram
如图10所示,对于新的等效谐振方程R′(s),可令其在谐振频率A点处的幅值增益等于KR,即让它在谐振点的增益等于其最终的稳定增益KR,由此便可以确定反馈增益K的值。
令s=j2πfres,带入R′(s)中得到

令R′(s)在谐振频率fres处的增益等于1+R得到
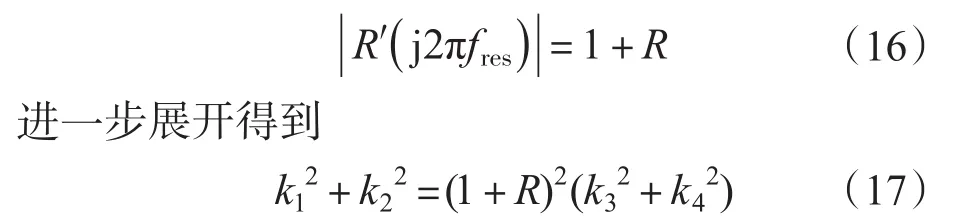
根据式(17)以及k1,k2,k3k4的表达式便可求得反馈环节系数K的值。
4 仿真验证
根据实际的电机参数和联轴器参数,选择仿真参数为:电机惯量Jm=1×10-3kg·m2,负载惯量JL=1×10-3kg·m2,等效弹性系数KS= 3 900 N·m/rad,等效阻尼系数KW= 0.003 N·m·s/rad。并在Matlab/Simulink系统中搭建电机谐振系统的仿真模型,并分别对系统加入观测器反馈前后进行仿真。
加入观测器反馈之前,给定速度指令为200 r/min,对系统进行仿真,得到电机侧和负载侧的速度如图11所示。
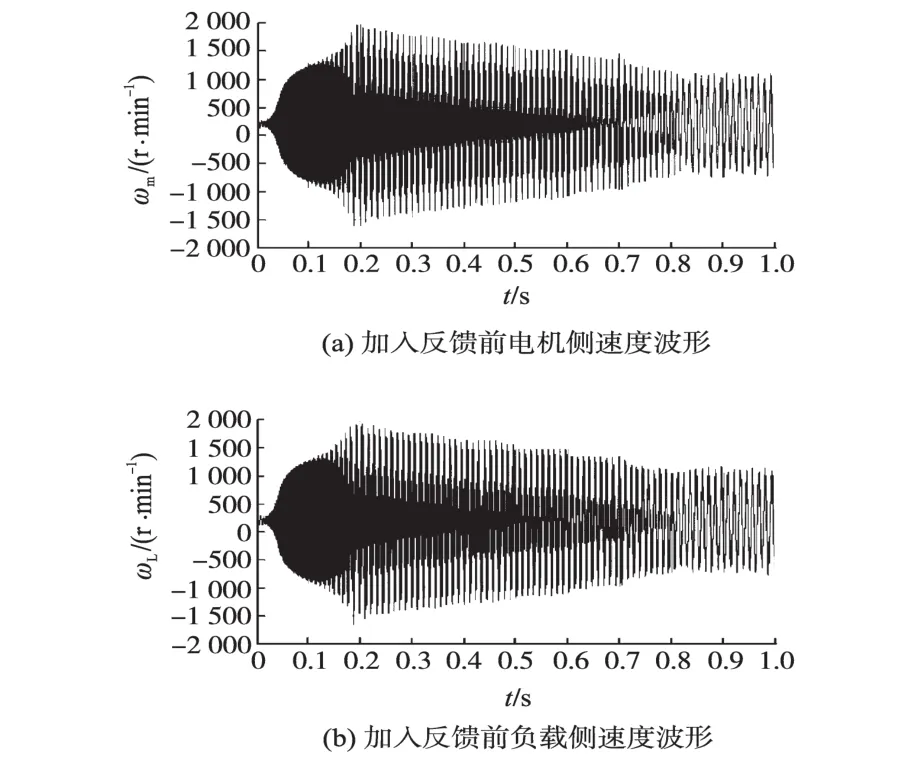
图11 加入反馈前电机侧和负载侧速度波形Fig.11 Motor and load speed of original resonance system
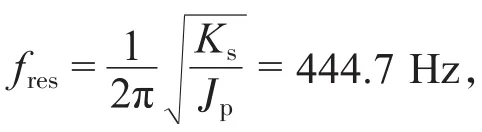
根据本文前面给出的反馈系数K的整定方法,按照系统给定的仿真参数计算反馈系数K的值,得到K =1 604。对加入反馈的系统重新进行仿真。图12为系统加入反馈后的仿真结果。
由图12可以看到,加入反馈以后,系统电机侧和负载侧的振荡都得到了有效抑制。这说明本文所提出的谐振抑制方案对抑制谐振是有效的。
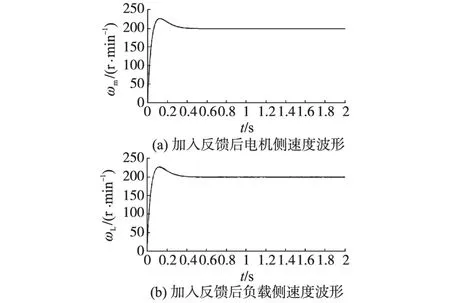
图12 加入反馈后电机侧和负载侧速度波形Fig.12 Motor and load speed of system with proposed feedback
5 结论
本文分析了伺服系统产生谐振的原理,在此基础上提出了一种基于扰动转矩反馈的谐振抑制方法,并详细分析了该方法抑制谐振的原理。本文还分析了反馈系数K对系统的影响,并给出了一种参数K的整定方法。最后,通过仿真,验证了本文所提出的方法对抑制谐振是有效的。
参考文献
[1]Ellis G,Lorenz R D. Resonant Load Control Methods for Indus⁃trial Servo Drives[C]//Industry Applications Conference,2000. Conference Recordofthe2000 IEEE,Rome,2000:1438-1445.
[2]Ellis G,Zhiqiang G. Cures for Low-frequency Mechanical Resonance in Industrial Servo Systems[C]//Industry Applica⁃tions Conference,2001. Thirty-sixth IAS Annual Meeting. Conference Record of the 2001 IEEE,Chicago,IL,USA,2001:252-258.
[3]Younkin G W. Compensating Structural Dynamics for Servo Driven Industrial Machineswith Acceleration Feedback[C]//In⁃dustry Applications Conference,2004. 39th IAS Annual Meet⁃ing.Conference Recordofthe2004 IEEE,2004:1881-1890.
[4]Sheng-Ming Y,Jin-De L. Observer-based Automatic Control Loop Tuning for Servo Motor Drives[C]//Power Electronics and Drive Systems(PEDS),2013 IEEE 10th International Conference on,Kitakyushu,2013:302-305.
[5]李杰.伺服系统惯量识别及谐振抑制方法研究[D].哈尔滨:哈尔滨工业大学,2008.
[6]Jian K,Songlin C,Xiaoguang D. Online Detection and Sup⁃pression of Mechanical Resonance for Servo System[C]//Intel⁃ligent Control and Information Processing(ICICIP),2012 Third International Conference on,Dalian,2012:16-21.
修改稿日期:2015-08-02
Suppression of Mechanical Resonance Based on Disturbance Torque Feedback
XIAN Minghui,LUO Xin,SHEN Anwen,LIU Feng
(School of Automation,Huazhong University of Science and Technology,Wuhan 430074,Hubei,China)
Abstract:Servo drives are used in a wide range of industrial applications,the flexible connection between motor and load may degrade the performance of the servo systems,and even cause instability. The reason of the mechanical resonance was analyzed and a method based on disturbance torque feedback was proposed to suppress mechanical resonance. The presented method utilizes the Luenberger observer to obtain the disturbance torque and the output of the observer was used as a feedback to the current loop after passing it through a proportional integrator. Moreover,a technique to calculate the feedback factor K was also presented and the validity of this method was verified by theory analysis. Finally,a servo resonance system simulation model based on Matlab/Simulink was established and the effectiveness of the proposed method is verified by the simulation results.
Key words:servosystem;resonancesuppression;disturbancetorquefeedback;Luenbergerobserver
收稿日期:2015-03-24
作者简介:咸明辉(1990-),男,硕士研究生,Email:xianmhhust@qq.com
中图分类号:TM341
文献标识码:A

