山地系统灾变行为自组织临界性研究

姚令侃, 黄艺丹

(1. 西南交通大学土木工程学院, 四川 成都 610031; 2. 高速铁路线路工程教育部重点实验室, 四川 成都 610031; 3. 抗震工程技术四川省重点实验室道路与铁道工程抗震技术研究所, 四川 成都 610031)

山地系统灾变行为自组织临界性研究

姚令侃1,2,3, 黄艺丹1,2,3

(1. 西南交通大学土木工程学院, 四川 成都 610031; 2. 高速铁路线路工程教育部重点实验室, 四川 成都 610031; 3. 抗震工程技术四川省重点实验室道路与铁道工程抗震技术研究所, 四川 成都 610031)

为了研究山地系统宏观动力学的整体规律，基于戴维斯地貌发育理论,提出处于地貌发育阶段幼年晚期的河谷及壮年期的山地具有自组织临界性(self organized criticality, SOC)的内禀属性,并建立了基于斯特拉勒积分的大流域地貌发育阶段判别方法.以地震触发崩塌滑坡为切入点,通过震区实震资料分析、元胞自动机模拟、振动台沙堆模型实验,提出不同烈度区地震触发崩塌滑坡分布的演化规律：在Ⅶ度、Ⅷ度、Ⅸ度区,崩塌滑坡规模与出现频率之间存在良好的负幂律关系，在Ⅹ度区,幂律关系弱化，在Ⅺ度区,这一关系转为对数正态分布. 通过3个案例介绍了SOC理论在岩土体地震扰动深度评估、泥石流防治工程设计径流量极值计算、基于地震活动性参数b值在地应力评估中的应用.

山地系统;自组织临界性;地震触发崩塌滑坡;元胞自动机

在非线性物理学中,作为灾变理论提出的前沿理论——自组织临界状态(self-organized criticality, SOC)理论,是P Bak等为解释无序的、非线性复杂系统的行为特征而提出的新概念.这类系统包含着众多发生短程相互作用的组元,并自发地向着一种临界状态进化.在临界状态下,小事件引起的连锁反应能对系统中大量数目的组元产生影响,从而导致大规模事件的发生.虽然发生的小事件比大事件多,但遍及所有规模的连锁反应是动态特性的一个必不可少的部分,所有时空关联函数都是幂律(power-law)的,因此幂律可以作为自组织临界状态的证据[1].

沙堆模型是SOC的范例.G A Held等采用在圆盘上逐粒加沙的方式构造沙堆,当沙堆的倾角在临界角附近时沙堆停止增长,此时,对新添加沙粒的响应是无法预测的,沙粒可能固定在沙堆上,也可能引起小范围沙粒的滑动,还可能导致更大规模的雪崩(avalanche),但总是呈现崩塌规模与出现频率成反比的幂律关系[2].

SOC的概念已被用于解释从山脉形成到股市波动等许多复杂现象.地震学是SOC最早关注的领域,如古登堡-里克特定律表明地震的频度与震级之间存在幂律关系.P Bak认为这种幂律来源于地壳系统的SOC,反之,也可把幂律作为地壳被锁定在永久临界状态的证据[3].在地学领域研究SOC是具有学科交叉性质的前沿研究,从宏观层面,於崇文院士以完整和独立的命题提出了固体地球系统的复杂性与自组织临界性[4],认为地质系统是自然界中的一种异常复杂的开放、远离平衡、相互作用的巨大耗散动力系统,具有自组织临界性的内禀属性,其时空行为服从地质作用的自组织临界过程动力学.从微观层面,许强等[5]论述了岩石破裂过程的自组织临界特征.

运用SOC理论认识和描述山地系统灾变动力学行为是本团队的主攻方向.国家自然科学基金委先后立项资助本团队开展了“散粒体自组织临界性”(2003)、“大尺度散粒体自组织临界性及其判据”(2005)、“地震触发崩塌滑坡自组织临界性”(2012)项目研究,这些题目也反映了本团队从散粒体材料层面至山地系统层面SOC性质的研究历程.本文主要以地震触发崩塌滑坡作为研究山地系统灾变行为SOC的切入点,开展一项专题研究,并介绍在应用领域开展的一些探索.

1 山地系统具备SOC性质的条件

1.1 SOC系统的必要条件

从现象学的角度,SOC系统应具有的必要条件是[6]:

(1) 系统是耗散的,包含大量(数目应在数百万个以上)发生短程相互作用的组元;大量自由度以某种均衡态势存在,不出现优势自由度而使系统仅有几个集体自由度来表征的现象.

(2) 组元之间最近邻位置相互作用,但存在着长程相关的关系.

(3) 系统自发地朝着临界状态进化,并将会永久性地或在一个有意义的时段内被锁定在这个状态.

(4) 系统同时具备两种动力学特征:一是敏感性,系统处于临界状态,微小的扰动也可能产生遍及全局的连锁反应;二是鲁棒性,系统的整体不受破坏.

(5) 所有的时空关联函数均为幂次.

从必要条件可看出,SOC系统的基本特征是以临界状态为动力学吸引子.即在外界持续的物质(或能量)供给条件下,广延耗散动力系统自发地向临界状态演化,一旦到达临界状态,将通过与外界能量的交换,永久性地或在一个有意义的时段内能被锁定在这个状态.这是从自然系统演化趋势角度提出的SOC基本条件,其特点是强调自然系统SOC的时段性.

但以上5条尚不能涵盖SOC系统需要满足的所有条件,还需要补充一些能够引起系统产生自组织到临界态的趋势的特定特征.

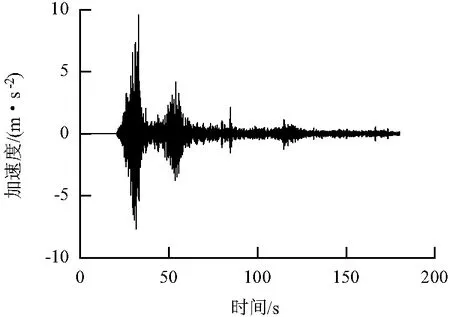
从构造性的角度,SOC行为只会在缓慢驱动的、相互作用占主导地位的阈值系统中出现.阈的存在使系统积累能量、应力和物质直至达到不稳定阈值.SOC 是慢驱动机制,即能量积累速率缓慢,而能量耗散的时间尺度远小于前者.以地震为例,地壳处于运动中,因而经受缓慢的形变,形变将导致岩石中应力的积累.如果在某些地方岩石不能再承受应力,就会发生突发事件,并向周围环境释放能量.如果环境可以承担这种能量的增加,那么这是一个孤立事件;如果环境也处在一种临界状态,就可能发生链式反应,地震就相当于应力释放的链式反应,涉及到比较大的区域.这两种过程的时间标度差别巨大,如“5·12”汶川大地震,专家估计应力在龙门山推覆构造带上的积累过程可能长达千年,地震时应力释放的主要过程仅在约100 s内完成[7].

1.2 基于戴维斯地貌发育理论的山地系统临界状态思辨

美国著名地理学家戴维斯(W M Davis)于1899年首次创立了侵蚀循环学说(theory of the cycle of erosion),认为地块从开始上升到被逐渐剥蚀夷平,直至降低到起伏不大的地面或者接近基准面的准平原之间,存在着连续的、同时又有阶段性的剥蚀过程和地表形态.在地表发育的过程中,Davis强调构造、作用和时间(侵蚀阶段)这3个要素之间的相互作用影响[8],进而将循环过程中的地形发展分为:地形起伏不大,河间地广阔平坦的幼年期;地面主要由谷坡和狭窄的分水岭组成的壮年期;具有残丘的准平原的老年期(图1).

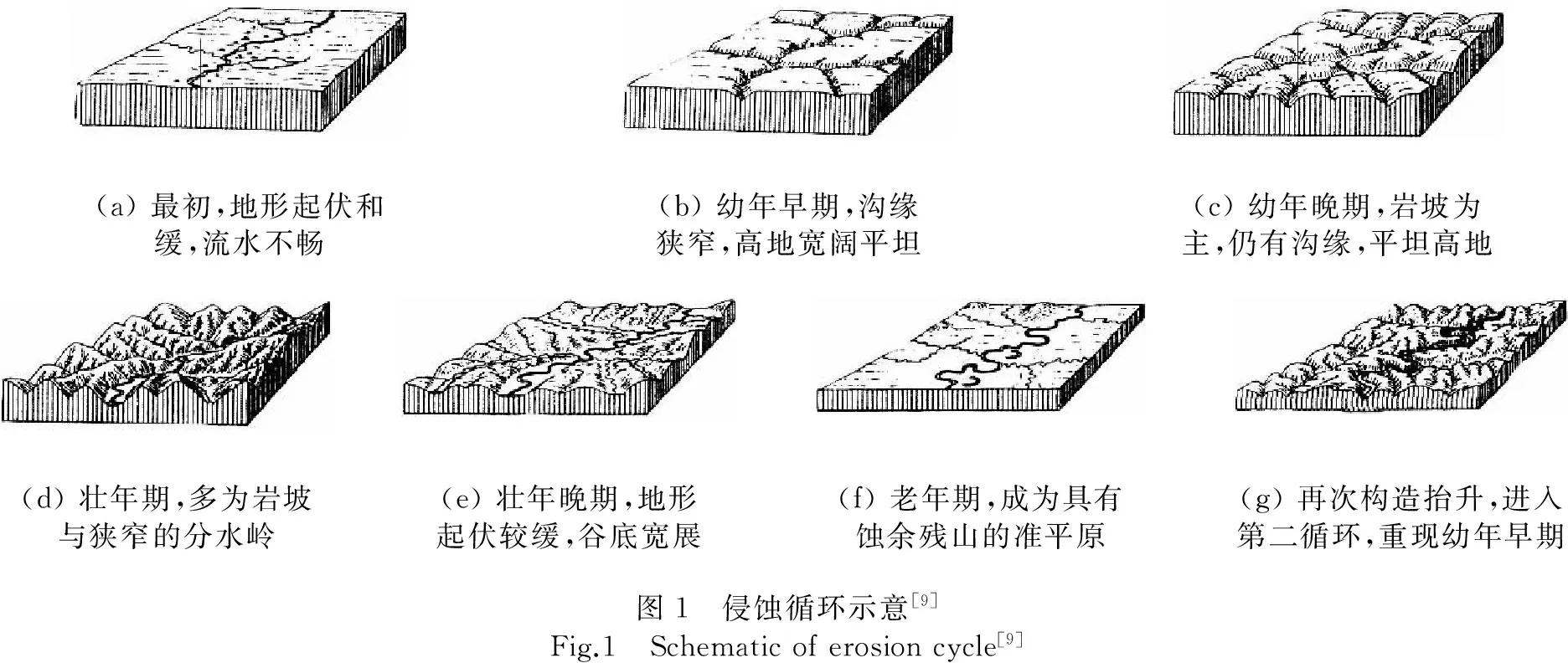
(a)最初,地形起伏和缓,流水不畅(b)幼年早期,沟缘狭窄,高地宽阔平坦(c)幼年晚期,岩坡为主,仍有沟缘,平坦高地(d)壮年期,多为岩坡与狭窄的分水岭(e)壮年晚期,地形起伏较缓,谷底宽展(f)老年期,成为具有蚀余残山的准平原(g)再次构造抬升,进入第二循环,重现幼年早期图1 侵蚀循环示意[9]Fig.1 Schematicoferosioncycle[9]

按照侵蚀循环理论,地貌发育循环过程中的地形变化如图2所示，图中，曲线L1、L2分别代表原始地面河谷的平均高度和分水岭的平均高度随时间的变化.虚线表示地壳短暂快速的抬升阶段,H1表示原始地形的起伏程度.

由图2可知,整个幼年期阶段直至壮年中期,河谷强烈迅速下切,河谷平均海拔持续下降,河谷之间由比较宽广的分水地发展为分水岭,平均海拔高度没有显著变化,因此,原始地面的起伏程度迅速增加,至壮年中期,起伏程度达到最大,分水岭与河谷之间的高差达到最大值H2.壮年期晚期和老年期阶段,河谷已经接近侵蚀基准面,高程基本没有变化,分水岭受到外营力的侵蚀而不断降低,分水岭变得浑圆低矮,直至准平原.

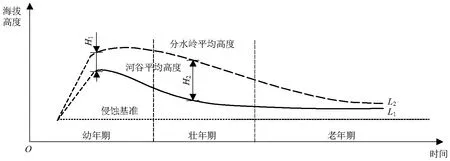
图2 Davis河流地貌发育图式(根据W. M. Davis)Fig.2 The sequence in the developmental changes of landforms of an ideal geographical cycle by W. M. Davis’s theory

地貌的形成和发展是内、外营力相互作用的结果.内营力趋向于使山体隆升,增强区域起伏程度,即使山体愈发陡峻;外营力趋向于使山体高度降低、削平,减弱区域起伏程度,即使山体愈发浑圆低矮.内营力是系统的,来自全球性的板块构造,可以认为其速度是确定的,而外营力是变化的.在新构造运动强烈的山区,山地隆升速度每年可达几毫米至十几毫米,山体剥蚀降低的速度小于地块隆升速度;但随着山体高度的上升,带来侵蚀基准面的降低,进而加大地表物质的重力作用和水流的下切侵蚀与搬运作用,外营力效应随之增强.外营力效应绝对量的增加必将导致内外营力作用的相对差距缩小,当地貌演化处于内外营力相当的阶段时,由于二者对山地地貌塑造的反向效应,山体坡度最大只能达到一个特定值,即所谓的临界坡度(对应于图2的H2时期),按照SOC理论,临界坡度成为该阶段山地斜坡系统演化的吸引子.

对照图1,虽然在一个侵蚀循环内,地貌将经历幼年期、壮年期、老年期,流域内的坡体相应经历向临界坡度发展、达到临界坡、偏离临界坡的演变过程,但处于地貌发育阶段幼年晚期地块的河谷(图1(c)),以及壮年期的山地(图1(d)),其斜坡系统能够保持在临界坡度,即在这一时段内已经演化到了临界状态.

若从构造性的角度,在漫长的地质过程中,地表形态的变化是组成地表的物质在渐变与突变的不断转化中进行的.渐变是指地形在漫长时间完成的变化过程,突变则是在急促的短时间内完成的变化过程.由于板块运动,在长达千百万年的时间尺度上使山脉隆升,将能量(势能)缓慢而持续地输入斜坡系统,使斜坡系统能量积累到临界状态,这一过程是非随机的;而在外营力随机扰动条件下,斜坡物质可能失稳并在重力作用下向下输移,即斜坡系统能量又通过突发性的山地灾害的方式耗散,这一过程是随机的.山地隆升驱动斜坡系统构造的速度(cm/a)和崩塌滑坡滑动速度(m/s)之间出现时间标度的巨大分离,相互作用为主导、阈动力学和慢驱动的有机结合,使得斜坡系统的演化成为自然界中SOC的良好实例.

综上所述,无论从现象学的角度,还是从构造性的角度,对照SOC的基本定义,可以认为当且仅当处于地貌发育阶段幼年晚期的河谷,如横断山三江并流区的高山峡谷地段(图3、图4),以及壮年期的山地,如龙门山(图5),山地斜坡系统成为这些区域地貌的主体,斜坡系统已经演化到了临界状态,SOC成为系统的内禀属性,它的灾变行为将服从SOC过程动力学.特别是崩塌、滑坡、泥石流等斜坡重力作用类地表过程,其共同特征是能量耗散以斜坡物质失稳下滑实现的,从物理概化角度,可认为沙堆模型是一种能抓住真实斜坡系统基本特征的简单理想模型,因而它们的动力学特征都应能在SOC 的概念框架下得到解释.

图3 三江并流区怒江河谷已演化到临界状态Fig.3 Nujiang river valleys in the three parallel rivers region having evolved to the critical state

图4 三江并流区澜沧江河谷已演化到临界状态Fig.4 Lancang river valleys in three parallel rivers region having evolved to the critical state

图5 龙门山已演化到临界状态,在强震作用下大面积崩塌Fig.5 Longmen mountains having evolved to the critical state, with lots of landslides triggered by earthquake

1.3 基于斯特拉勒积分的山地系统发育阶段判别方法

以上提出了以地貌发育阶段作为界定山地系统具有SOC性质的适用范围,应用中还必须建立地貌发育阶段的定量判别方法.

1952年,斯特拉勒(A N Strahler)提出侵蚀流域的面积-高程分析方法[10],可以定量推求Davis的地貌发育阶段.面积-高程曲线分析法是描述一定高度范围内的面积随相对高度变化所表示的曲线及其所围成的面积,相对高度可以确定侵蚀过程的强度,而残留的面积可以代表这种强度下地貌的保持能力,因此,可以说面积-高程曲线提供了地貌的发育信息[11].

记流域内等高线的值和最低点之间的高差为h,每条等高线以上的面积为a,全流域面积为A0,流域内最高点和最低点之间的高差为H,分别以

X=a/A0,

(1)

为横坐标和纵坐标画图,可以得到曲线

Y=h/H,

(2)

也就是面积-高程曲线,称为斯特拉勒曲线(the Strahler’s curve).

设定积分

(3)

式中:

S为斯特拉勒曲线与坐标轴包围的面积,称为斯特拉勒积分(the Strahler’s integral).

用S值推求侵蚀流域地貌演化阶段,即:

S>0.60,幼年期;

0.35≤S≤0.60,壮年期;

S<0.35,老年期.

由于斯特拉勒积分为无量纲参数,因此,曲线可以描述和比较不同规模的流域,但必须是在流域内地貌处于同一发育阶段的前提下,所以,斯特拉勒积分应用于小流域一般没有问题.然而,对于大型山区河流,不同河段可能处于不同的地貌单元,这与Davis循环理论中流域内的各个部分同时发育的假定是相悖的,不能直接应用该方法.

作者提出包含不同地貌单元的大流域斯特拉勒积分计算方法:

首先确定计算区域,通过选择河道控制点(也就是计算流域的出口点),确定适用于Davis侵蚀循环理论的范围.选择河道控制点的原则为:

① 控制点以上的流域是灾势评估的研究区;

② 河道控制点以上的流域应基本上处于同一地貌单元.

然后利用DEM和ArcGIS技术,获得斯特拉勒曲线的横、纵坐标值.具体方法是在具有规则格网的DEM上,对研究区域内所有大于某个高程值的栅格单元个数进行累加,再乘以栅格单元的面积A0,即得到该高程值以上的面积[12],如式(4)所示.

(4)

式中:

Ah0为等高线值为h0以上的面积;

Nh为研究区域内高程值为h的栅格个数.

以(Ah0/A,h0/H)为横、纵坐标值,绘制斯特拉勒曲线,可计算得到斯特拉勒积分.

现举例说明基于斯特拉勒积分的山地系统发育阶段判别方法.2010年4月14日,我国青海省玉树县发生Ms7.1级地震，影响流域主要水系包括通天河、扎曲、巴曲等,地形以高海拔、低起伏为主.震区位于通天河和金沙江的交汇地段,圈定的研究区域的流域包括沱沱河、通天河、金沙江上游在内的长江上游河段,研究区域的水系格局如图6所示.

图6 研究流域及周边流域、裂点位置、计算流域区域图Fig.6 Region graphs of the study basin and its surrounding basin, the knick point location, and the computation basin

由于青藏高原的分阶段、非均一隆升,使高原东缘的外流河产生溯源侵蚀,并形成新的河谷,它与未被溯源侵蚀的老河谷交替的地方,河床坡度突然增加,形成裂点[13],裂点上下游的河谷往往处于不同的地貌发育状态.通过提取河道的纵剖面图(图7)可以看出,在海拔4 000 m的地方存在裂点.目前青藏高原普遍存在着高原面、盆地面两级夷平面.盆地面是青藏高原形成于上新世纪初至上新世纪末的第二级夷平面,盆地面内平坦开阔,切割微弱.位于裂点以上的金沙江上游谷地是溯源侵蚀尚未达到的地方,这一地区的盆地面保存完整,较少切割.裂点以下的金沙江河谷位于我国地形最为陡峻的横断山区,河流切割成深邃的峡谷.裂点上、下游两个地貌单元差异明显[14].又因玉树地区处于该裂点的上方,可满足上文提出的选择河道控制点的两条原则，故决定选择该裂点为计算流域的出口点,绘制斯特拉勒曲线,计算斯特拉勒积分S=0.32,如图8所示.图8表明,震区内流域属于壮年晚期发育阶段,宽谷缓丘是主要地貌特征.在玉树地震时,地震触发的崩塌滑坡无论从规模还是数量上,都远小于汶川地震和芦山地震,认为地貌发育阶段不同是玉树地震崩塌滑坡灾害小于汶川、芦山地震的主要因素(汶川和芦山地震区均处于壮年期).

图7 研究河流纵剖面图Fig.7 Longitudinal profile of the study river

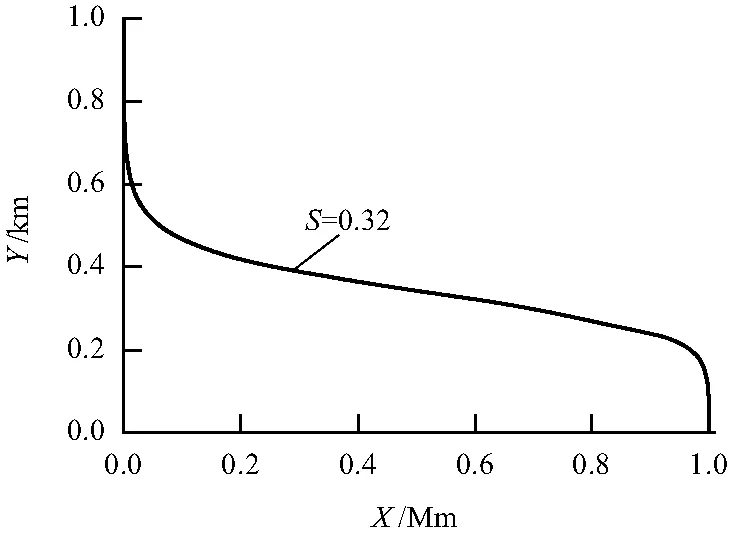
图8 计算区域的斯特拉勒曲线Fig.8 Strahler curve of the computation basin

反之,若按图6所示的全河段计算相对应流域的斯特拉勒积分,得S′=0.53,据此推断整个流域的发育期处于壮年期,应该是坡陡谷深的地貌,显然与震区的自然景观不符.至此,解决了斯特拉勒分析方法只能适应于小流域的问题,建立了山地系统发育阶段的定量判别方法.

2 不同烈度区地震触发崩塌滑坡分布规律

发生在四川龙门山地区的“5·12”汶川地震、“4·20”芦山地震,是人类有现代观测仪器以来,地震触发崩塌滑坡数量最多、资料最翔实的两次大地震,震后有关地震触发崩塌滑坡的研究成为热点课题,但国内外大多数研究集中在对该场地震崩塌滑坡灾害的统计、地震触发崩塌滑坡形成的力学机理等方面,缺少从物理学层面对其总体特征进行描述的整体理论.

龙门山是青藏高原边缘山脉中的陡度变化最大的山脉,在30多公里范围内海拔从700 m升高到5 000 m.晚新生代中新世以来,龙门山至少有5～10 km的底层被剥蚀掉,上升速度约达0.6 mm/a.近年来的地形变化资料表明,该构造带的九顶山地区正以0.3～0.4 mm/a速度持续上升[15]，这种隆升和夷平的持续作用,造成龙门山河谷深切、地势陡峻的地貌景观.龙门山整体处于地貌演化的壮年早期,斜坡系统已经演化到了临界状态,这就是能在SOC的概念框架下,研究汶川地震、芦山地震触发崩塌滑坡整体分布规律的前提条件.为此,选择地震触发崩塌滑坡作为研究山地系统灾变行为SOC的切入点,在原型问题的物理代表性、资料拥有量等方面,均具有独特的优势.

2.1 地震触发崩塌滑坡实震资料分析

利用震后遥感影像资料进行人工目视解译是大面积获取地震触发崩塌滑坡信息的主要方法,由于使用的遥感影像资料精度不同、判识人员的判识标准和经验不同等,对同一区域的判识可能会出现较大差异,因此,现场调查工作不可忽视.但以上细节并不是关键问题,影响地震触发崩塌滑坡分布规律最具控制性的因素是地震烈度,在研究崩塌滑坡分布规律时,应该按地震烈度区分别统计.

汶川地震后,获取2008年6月4日的ALOS卫星影像(分辨率为10 m),覆盖范围约为9 750 km2(30°58.78′N～32°2.3′N,103°33.97′E～104°36.17′E),包括北川、汶川、茂县、都江堰等区域.另外,还通过下载获得汶川震前TM卫星图片.由于这套ALOS遥感数据资料Ⅸ度以下烈度区云层覆盖率高,因此,仅对Ⅸ度及以上烈度区进行崩塌滑坡的遥感解译工作.在上述区域内,采用人机交互的目视解译技术,辅以野外实地调查,判译出地震触发崩塌滑坡9 341处,解译结果如图9所示.

芦山地震后,通过多种途径收集和购买了震区航空、航天遥感影像资料,主要包括中国科学院遥感与数字地球研究所提供的三批航片图(拍摄时间为2013年4月20日和21日,其中,第一批影像分辨率为0.6 m,第二、三批影像有0.4 m和2 m两种分辨率);购买的资源三号卫星影像(拍摄时间为2013年5月13日,分辨率为2.1 m).对以上遥感影像资料进行几何纠正、融合、拼接、图像增强处理后,获得芦山震区遥感数据5 655 km2(102°27.68′E～103°30.84′E,29°44.54′N～30°26.91′N),包括邛崃市、名山县、雨城区、芦山县、天全县、宝兴县、荥经县等区域.在上述区域,对地震触发的崩塌滑坡灾害点进行逐一解译,并结合实地考察检验解译结果,最终确定地震触发崩塌滑坡1 608处,解译结果如图10所示.

图9 汶川地震触发的崩塌滑坡分布示意图Fig.9 The distribution map of landslides induced by Wenchuan earthquake

按不同烈度区,分别对汶川Ⅸ度、Ⅹ度、Ⅺ度,芦山Ⅶ度、Ⅷ度、Ⅸ度区的崩塌滑坡进行统计分析,以崩塌滑坡面积(A)作为规模的度量,分析崩塌滑坡规模与发生频率之间的关系.由于芦山地震各烈度区的遥感影像资料更为完备(Ⅸ度区遥感覆盖面积为100%，Ⅷ度区遥感覆盖面积为94.5%，Ⅶ度区遥感覆盖面积为59.4%),故芦山震区增加了崩塌滑坡点密度这一指标,统计结果见表1.

由表1可看出：汶川Ⅸ度区,地震触发的崩塌滑坡面积与出现频率之间呈现良好的幂律关系(R2=0.916);汶川Ⅹ度区,崩塌滑坡面积与出现频率之间幂律关系式的相关系数下降到0.906,可以认为基本服从幂律关系;汶川Ⅺ度区,崩塌滑坡面积与出现频率之间的关系符合对数正态分布;芦山Ⅶ度、Ⅷ度、Ⅸ度烈度区,崩塌滑坡规模与发生频率之间均服从幂律分布,且幂指数b值相近.芦山地震不同烈度区震害的主要区别是:随地震烈度的减小,崩塌滑坡点的密度单调减小.

汶川地震、芦山地震是我国迄今为止获得地震山地灾害资料最全、精度最高的大地震,据此得到不同烈度区地震触发崩塌滑坡的统计结论,作者更加关注该结论是汶川地震、芦山地震的独特现象,还是具有普适性意义的规律.因此,在SOC的概念框架下,利用元胞自动机模拟方法,结合振动台沙堆模型物理实验,对上述实震资料显示的统计规律,从物理层面诠释其机理.

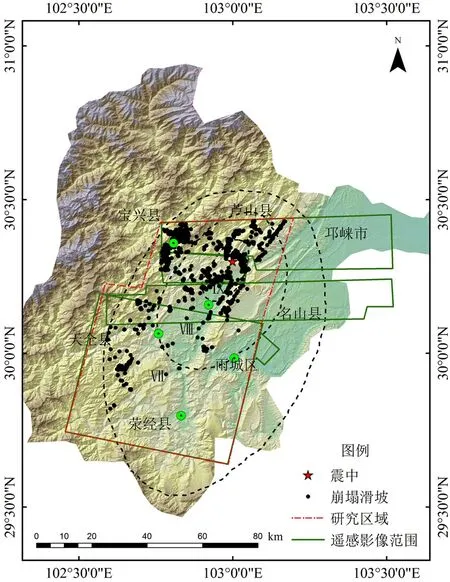
图10 芦山地震触发的崩塌滑坡分布示意图Fig.10 The distribution map of landslides induced by Lushan earthquake

2.2 地震触发崩塌滑坡元胞自动机模拟

元胞自动机(cellular automata或cellular automaton, CA)是空间和时间都离散,物理参量只取有限数值集的物理系统的理想化模型[16].该模型以规则网格形式分布、空间离散的元胞个体为基本单元,元胞遵循一定的演化规则作同步更新来模拟真实的物理系统,特别适合复杂系统时空演化过程的动态模拟研究.

模型方法在SOC的研究中具有非常重要的地位,目前所有对沙堆生长与坍塌机理的模拟算法都是以元胞自动机为数学基础,对SOC的理解也大部分来源于元胞自动机沙堆模型的数值模拟.处于青壮年期的山地系统具有SOC的内禀属性,因此,可以构建地震触发崩塌滑坡沙堆模型,用元胞自动机来模拟.

根据原型问题的物理特征,与传统沙堆模型相比,地震触发崩塌滑坡的沙堆模型应具有以下特点[17]:

(1) 传统沙堆模型考察的是一个沙堆在受到多次扰动下坍塌规模随时间的分布规律.地震发生时,同时引发多处崩塌滑坡,需要考察多个沙堆在同时受到一次扰动时坍塌规模的分布规律.

表1 不同地震烈度区地震触发崩塌滑坡统计Tab.1 Statistics of landslides in zones with different seismic intensity

(2) 在传统沙堆模型中,沙堆是局部受到扰动，在地震触发崩塌滑坡问题中,坡体是整体受到扰动,因此,模型需要采用系统整体受扰的方式.

(3) 传统沙堆模型均是在同一微扰条件下观察系统的动力学行为.而地震触发崩塌滑坡,首先不同烈度区,地震对坡体的震动力是不同的,其次地震力相对坡体已超过微扰量级,因此,设计不同扰动强度,来模拟这一物理现象.

(4) 传统沙堆模型,外界对系统的输入是物质(添加沙粒),发生连锁反应时,扰动的传播是物质的传播,遵守物质守恒原则.在地震触发崩塌滑坡的问题中,外界对坡体系统输入地震力,坡体失稳需要克服其自稳能力,会消耗一部分输入的能量,扰动的传播是能量的传播,并且存在着能量耗散.

根据以上特点,构造地震触发崩塌滑坡元胞自动机沙堆模型,基本算法步骤如下:

步骤1 生成沙堆.地震触发崩塌滑坡相当于考察大量沙堆,同时受到一次地震作用时坍塌规模的整体分布规律,因此,一次性生成N个沙堆,每个沙堆规模相等,但初始状态不同.对于每个沙堆而言,考虑一个L×L的二维系统,用(i,j)代表元胞所处的位置(其中, 1≤i,j≤L),每一个元胞有上、下、左、右4个邻居,Fi,j为反映元胞(i,j)稳定性的状态值(相当于元胞的能量).所有元胞赋予一个0到阈值Fth之间的初始值,且取随机数.

步骤2 沙堆演化到临界态.每个沙堆按照下列规则连续反应,直到所有沙堆演化到临界状态.

① 找到最大状态值Fmax的元胞,把每个元胞的状态值都增加Δ=Fth-Fmax(相当于对整个系统的一个扰动),即Fi,j→Fi,j+Δ;

② 若新的Fi,j大于或等于设定的阈值Fth,即Fi,j≥Fth,则该元胞倒塌,并向邻居传播扰动,重新分配Fi,j给它的4个最近邻:

Fi±1,j→Fi±1,j+αFi,j,

Fi,j±1→Fi,j±1+αFi,j,

Fi,j→0;

(5)

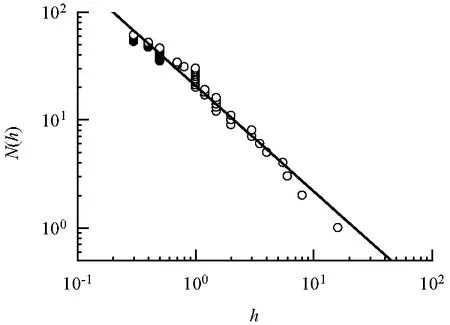
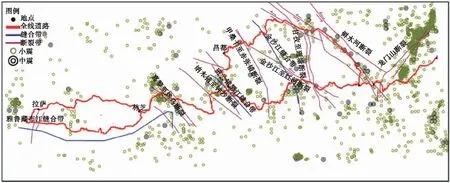
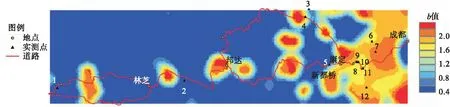
③ 这种扰动传播可能会导致链式反应,如果由于元胞(i,j)的倒塌导致它的邻居变得不稳定,重复②直至所有的元胞状态值小于阈值(Fi,j

通过步骤2,产生N个均处于临界状态,但各元胞状态值不同的沙堆.

步骤3 对N个沙堆同时施加一次扰动.令F′为扰动强度,每个沙堆的元胞状态值都统一增加F′,即Fi,j→Fi,j+F′.元胞之间的相互作用仍按照规则②、③执行.

步骤4 改变扰动强度F′,重复步骤3,获得沙堆在不同扰动强度下坍塌规模与发生频率的关系.

需要说明,按照Δ=Fth-Fmax施加扰动时,一般只会直接触发一两个元胞,但扰动强度加大后,可能会触发一批元胞,它们各自都可能引发链式反应,这些链式反应在空间上也会有交叉现象.因此,在算法上采用并行处理,所有受扰元胞在同一时步内按照平行更新的方式反应,通过记录倒塌的元胞数目,作为沙堆坍塌规模的度量.

模型参数取为:α=0.2,Fth=1,L=50.

实验生成100万个沙堆(N=106),先连续反应106次(均取F′=1-Fmax),以确保沙堆演化到临界状态.然后取

F′=0.000 01,0.000 02,0.000 04,0.000 08,

1-Fmax,0.001,0.005,0.01,

开展了8组模拟实验.令沙堆坍塌规模为S,分析坍塌规模与发生频率的关系,雪崩密度等于发生坍塌事件的沙堆数除以总沙堆数,实验结果见表2.

表2 元胞自动机模拟实验结果Tab.2 Results of cellular automata simulation

由表2可看出,以扰动强度1-Fmax为界可以划分为两个区间,沙堆模型的动力学特性呈现出不同的性质:在扰动强度小于1-Fmax的区间,当F′从0.000 08逐渐减小到0.000 01时,随扰动强度的降低,坍塌规模与发生频率基本服从同一幂律分布(表2),但随扰动强度的减小,雪崩密度单调减小(图11);在扰动强度大于1-Fmax的区间,当F′从0.001逐渐增加到0.01时,随扰动强度的增加,沙堆模型的动力学特性将经历幂律—幂律弱化—对数正态分布的渐进式的演变过程(图12).

对照两次地震的实震资料统计结论,汶川地震Ⅸ度区崩塌滑坡规模与出现频率之间的关系可用幂律描述,Ⅹ度区这一关系基本服从幂律分布,Ⅺ度区更偏向于对数正态.芦山地震Ⅶ-Ⅸ度烈度区地震触发崩塌滑坡规模与频率均服从幂律分布,但随地震烈度的减小,崩塌滑坡点密度单调减小.通过以上元胞自动机模拟,证明了不同烈度区地震触发崩塌滑坡的分布规律存在必然的联系性,这些现象均来源于山地斜坡系统具有SOC内禀属性的物理机制,从而实现了从物理角度对“5·12”汶川地震、“4·20”芦山地震不同烈度区,地震触发崩塌滑坡分布规律演变机理的诠释,初步建立了不同烈度区地震触发崩塌滑坡总体特征的完整表征体系.

2.3 地震触发崩塌滑坡振动台沙堆模型实验

元胞自动机数值模拟是获得SOC系统性质的主要途径,但相对地震触发崩塌滑坡的原型问题,无疑是一种高度概化的处理,因此有必要配合沙堆模型物理实验相互印证.

利用大型地震模拟振动台,输入精确可控的地震波,开展动力扰动下的沙堆模型实验,使之更加逼近物理原型.实验设备为西南交通大学高速铁路线路工程教育部重点实验室的电液伺服驱动地震模拟振动台.在振动台上放置一长2.58 m、宽1.50 m、高1.95 m的箱体,选用粒径为0.6～50.0 mm经过筛分的干燥天然沙石在箱体里堆成一个单面坡沙堆,总重量达6.8 t(图13).

图11 雪崩密度ρ与扰动强度F′Fig.11 Avalanche density ρ vs disturbance intensity F′

图12 不同扰动强度下坍塌规模的概率密度曲线Fig.12 Probability density curves for different disturbance intensities

图13 沙堆模型Fig.13 Sandpile model

向振动台输入汶川地震卧龙台站记录的修正波(图14),模拟地震对沙堆的扰动.取峰值加速度为0.075g、0.100g、0.125g、0.150g、0.200g、0.350g、0.450g,开展了7组实验.

图14 汶川地震卧龙台记录修正波Fig.14 Modified Wenchuan acceleration wave recorded by Wolong station

每组实验步骤如下:

步骤1 在箱内堆成单面坡沙堆,坡面靠沙粒的重力下滑自然形成,使坡脚达到开口端边缘,沙堆达到临界坡度;

步骤2 输入指定峰值加速度,称量从坡脚处落入落沙收集槽的沙粒重量,作为该组的一次实验值;

步骤3 每次实验后,将落沙收集槽内的沙粒补充回沙堆上,确保沙堆始终处于临界状态;

步骤4 重复步骤2、3,每组实验不少于60次.

以落沙收集槽内沙粒的重量作为规模的度量,令沙粒重量为x,分析坍塌规模与发生频率之间的关系,坍塌密度等于发生坍塌事件的实验次数除以总实验次数,实验结果见表3.

由表3可看出,当输入地震波峰值加速度为0.075g、0.100g、0.125g时,落沙量与发生频率均服从幂律分布,但随峰值加速度的减小,坍塌密度单调减小;当峰值加速度增加到0.15g～0.25g时,落沙量服从对数正态分布;当峰值加速度增加到0.35g～0.45g时,该阶段样本表现为具有正态分布的曲线特征.

振动台沙堆模型实验得到了与地震实震现象规律和元胞自动机模拟类似的结论,更进一步,虽然目前尚未获得Ⅻ度区的实震资料,但不妨预测应具有向正态分布发展的趋势.

振动台沙堆模型实验的物理过程更接近地震触发崩塌滑坡的原型问题,虽然实验次数有限,但仍然对作者提出的不同烈度区地震触发崩塌滑坡分布规律的普适性提供了有力支持.

表3 振动台沙堆模型实验结果Tab.3 Results of the shaking table test of sandpile model

3 应用案例

具有SOC性质的系统,在临界状态下受到一系列微小而均匀的扰动,每次扰动下表征反应规模的物理量可用幂律描述,这种幂律关系将灾害学的研究与物理学联系在一起.规模与频率的幂次定律描述的是某种量级灾害发生的数目,这种灾害演变总体规律在灾势分析、风险评估和危险性区化中的应用,是SOC较为明确的应用领域,对此举一例进行说明.

除此之外,还将介绍两个属于应用技巧层面的案例,旨在说明SOC存在更广阔的应用前景.

3.1 岩土体地震扰动深度评估

汶川大地震后,在震区调查时,观察到在无深大结构面控制的情况下,道路边坡地震失稳一般表现为浅表的崩塌滑坡,具有“剥皮型”灾害特点.与日本OYO公司合作,采用面波仪对国道213线都江堰至映秀段(含水磨支线)震后边坡进行了勘察,发现自然坡体0～5 m范围内的表层剪切波速为250 m/s,明显低于下部土体的波速,判定为汶川地震的强扰动范围[18].但仅以这些表观认识和有限的测量数据为依据,提出具有普遍性和包容性的结论是困难的.为此对照1∶2 000的地形图,对沿线公路边坡进行详查,内容涵盖沿线公路边坡崩塌滑坡的规模(崩塌滑坡方量)、崩塌滑坡体深度、工点经纬度、高程、岩性以及原有工程措施.灾害类型主要包括砂岩边坡滑坡,岩质边坡崩塌,崩坡积体、残坡积体、冲洪积体等浅层崩塌滑坡.

调查中发现不同崩塌体的崩塌深度存在很大区别.在Ⅸ度裂度区调查的61个崩塌体中,崩塌深度小于0.5 m的27个、0.5～1 m的15个、1～2 m的11个、2～5 m的4个、5～10 m的3个、10 m以上的1个,平均崩塌深度为1.2 m.

令崩塌滑坡体深度为h,深度大于h的工点数为N(h),通过回归分析,拟合曲线如图15所示.由图15可以看出,h与N(h)在双对数坐标图上近乎一直线,关系式为

N(h)=20.27h-0.994 5.

(6)

由式(6)可知,相关系数R2=0.973,表明Ⅸ度裂度区崩塌滑坡深度与出现频率之间存在良好的幂律关系,说明在Ⅸ度区地震触发崩塌滑坡深度也存在SOC特性.这样若仍以平均崩塌深度作为岩土体地震扰动深度的表征已不合理.

式(6)为Ⅸ度裂度区崩塌滑坡体深度h与大于h的工点数N(h)之间的幂律回归关系,当样本数量足够大时,在统计意义上可得随机变量h的分布函数.如据实震调查资料可初步作出h的概率分布如图16所示.

由图16可知,汶川地震Ⅸ度裂度区93%的崩塌滑坡体深度均小于5 m,这是基于SOC理论开展的工作,其意义在于建立的是以物理理论为基础的统计模型,跨越了仅据典型样本得出统计关系的层面,其规律具有普适性,可以作为汶川地震Ⅸ度区地震对坡体强扰动效应的定量表征.图16所示的分布规律可为汶川震后次生山地灾害物源条件估算以及确定边坡灾害防范深度提供指导.

图15 汶川地震Ⅸ度区崩塌滑坡深度累积分布Fig.15 Log-log plot of landslides number and depth in zones with seismic intensity Ⅸ

图16 汶川地震Ⅸ度区崩塌滑坡体深度概率分布Fig.16 Probability distribution curve of landslide depth in the zone with s eismic intensity Ⅸ in Wenchuan earthquake

3.2 泥石流径流量的极值计算

在工程规划与设计中,常常需要对未来工程服务期内情况进行预测,包括对外荷载最大值的预计.但人们往往仅掌握有限时段的观察极值,如每年洪水的最大值.为实现从以前观测到的极值数据运用外推法求得工程服务期内的极值统计问题,在数学统计学中已建立了极值统计这一领域,重要成果之一是来自带有指数型衰减尾部的初始分布的极值将渐近地收敛于Ⅰ型极限形式[19].在以下的研究中,基于泥石流径流量的频率-规模可用幂律描述关系,通过数学上的映射,将其转换成带有指数型衰减尾部的分布,从而达到了运用Ⅰ型极限形式的条件,据此建立了不同设计基准期蒋家沟泥石流最大径流量极值分布的数学模型.

一场泥石流的总径流量是反映泥石流规模的主要表征值,也是开展泥石流拦挡工程容量设计、泥石流堵河可能性预测等工作的关键参数.实际工程中,关注的是在工程设计基准期内可能出现的泥石流径流量的极大值,这些极大值可用具有一定概率分布的随机变量来模拟,但在缺少长序列观测资料的情况下,确定极值概型是极为困难的.

极值理论是处理一定样本容量极端值分布特性的理论,其基本概念为:对{Xt,t∈T}随机变量族,将时间域T等分为n个时段,每个时间段τ=T/n,则得n个独立的随机变量ηi(i=1,2,…,n),每个随机变量都有相同的分布函数F(x).在这个随机变量族中,极大值为

M=max(x1,x2,…,xn).

(7)

在上述两个假定(独立、具有相同的分布函数)的前提下,极大值的分布函数为

FM(x)=p(M≤x)=

p(η1≤x,η2≤x,…,ηn≤x)=

(8)

式中:F(x)为初始分布.

若F(x)的密度函数为f(x),则有

fM(x)=n[F(x)]n-1f(x).

(9)

由于FM(x)与初始分布F(x)有着密切的关系,这样在随机变量的初始分布以及样本容量n已知时,可写出极值概率的确切分布.但在通常情况下,确切分布的求解十分困难,在工程实际应用中,常用做法就是使用极值的渐近分布.所谓渐近分布,就是当数目n趋于无穷大时,概率分布的极限形式,即渐近分布将收敛于确切分布,这样可用渐近分布代替实际难以获得的确切分布.

根据Gumbel的研究[20],极值分布的渐近形式并不取决于初始分布的精确形式,主要决定于初始分布在极值方向的尾数表现,初始分布的中央部分对极值分布的渐近形式影响很小,但是,极值参数则决定于初始分布的形式.工程上常用的渐近分布有3种类型,其中最大值的Ⅰ型渐近分布多用于荷载的极值统计方面,如桥梁使用荷载、风速、地震震级、洪水流量等.

在泥石流研究领域,P A Johnson等研究表明[21],泥石流规模与频率之间存在幂律关系,是自组织临界状态系统的行为标志.艾南山等认为[22]在泥石流的形成区松散堆积物组元间的非线性作用,使系统自然地朝着临界状态演化,在临界状态时,诸如降水等外界的细微扰动将被放大而导致规模不等的泥石流暴发,这种耗散动力学系统的行为特征,可以用自组织临界状态的概念加以解释.王裕宜[23]从泥石流土体的应力应变自组织临界特性触发,认为粘性泥石流具有自组织临界性.按照SOC系统的定义,泥石流径流量规模W与频率N之间应服从幂律分布,即N=aW-b.假设在所统计资料中,规模W的最大值和最小值分别为Wmax和Wmin.设X=lnW,则

N=a0e-bX,

(10)

式中:a0为常数;b为幂指数;X≥Xmin,Xmin=lnWmin,一般可取为0.

由频度代替概率的思想,得出X的分布函数为

1-e-b(x-Xmin).

(11)

利用极值分布的最大吸引场的定理[24],可以判定上式极值分布的极限形式为收敛于Ⅰ型的渐近分布,进而推出X极大值的极限分布函数为

FM(x)=exp(-exp(-α(x-μ))),

(12)

相应的概率密度函数为

FM(x)=αe-α(x-μ)exp(-exp(-α(x-μ))),

(13)

α=c2/σQ1=1.28255/σQ1,

(14)

F1(x)=exp(-exp(-3.042×10-6×

(x-538 680))).

(15)

当设计基准期T=50 a时,已知年最大径流量的分布,统计时段为1 a,τ=1.n=T/τ=50.根据极值I型分布的特征可知,设计基准期最大泥石流径流量分布的标准差与初始分布相同

σQ50=σQ1=421 620 m3.

均值平移距离为

均值为

这样可得设计基准期为50 a时,蒋家沟泥石流最大径流量的概率分布为

F50(x)=exp(-exp(-3.042×10-6×

(x-1 824 684))).

(16)

同理可推出设计基准期为100、300 a时,蒋家沟泥石流最大径流量的概率分布为

F100(x)=exp(-exp(-3.042×10-6×

(x-2 052 542))),

(17)

F300(x)=exp(-exp(-3.042×10-6×

(x-2 413 690))).

(18)

概率密度曲线如图17所示.

图17 蒋家沟不同设计基准期的径流量极值概率密度Fig.17 Probability density curve of extreme runoff values in different design base periods of Jiangjia ravine

3.3 基于地震活动性参数b值的地应力评估模型

系统动力学服从幂律是人们对SOC系统的基本认识.但幂指数b不仅仅是一个统计分析参数,还是反映系统动力学特征与活跃度的主要指标,不同系统b值的差异或者同一系统b值的演化,有着重要的物理意义.以下基于地震活动性参数b值与地应力的反相关关系,推求区域地应力的研究,虽然是一种统计层面的工作,但借此说明,从幂律到b值的讨论,有可能开拓出SOC更广阔的应用空间.

地应力是长大深埋隧道工程设计所需的重要参数,现场钻探是获得准确初始地应力的可靠手段,但是在铁路选线的可行性研究阶段,由于线路方案尚未确定,不宜开展大规模的地应力现场钻探工作,因此,地应力评估模型的发展就成为具有明确应用背景的课题.

目前,在地应力场分布特征的研究中多采用统计实测地应力、建立回归模型的方法来分析主应力随埋深的分布规律.主要代表性的工作有:中国科学院武汉岩土力学研究所对中国大陆地区实测地应力沿埋深分布规律做的相关研究[29];中国地震局地壳应力研究所根据统计的地应力实测数据对中国陆域八大地块水平主应力随埋深分布规律进行的回归分析[30].但是上述研究工作提出的回归模型,由于公式仅有一个自变参量,即埋深H,当模型的统计样本未涵盖评估区域时,就可能造成较大误差.若能在回归模型中引入能反映当地地应力状态的参数,则可望通过增加信息量的手段,提高计算精度.

3.3.1b值与地应力的关系

在前述的古登堡-里克特定律中,a反映平均地震活动水平,b反映大小地震的比例关系.随后,在地震预报领域,分析发现，大震前震源及附近区域经常会出现某些震级档内的地震增多或减小,导致出现大小地震比例失调、b值减小的异常现象.由于区域应力积累水平升高是大地震发生的必要条件,因此,b值也反映了地应力状态,且二者呈反比关系.

之后有学者[31-33]根据单轴压缩试验过程中产生的声发射(AE)现象对上述假说进行了验证.岩石的声发射现象描述为:岩石受力变形时,在岩体内原先存在或新产生的裂缝周围形成应力集中,这些局部应力集中区不均匀发展,并发生突然的破裂,从而向四周辐射弹性波.声发射活动与地震活动的机制最为接近,在统计参数上与地震活动性的可对比性也最强,具体表现为:实验记录到的声发射次数与声压幅值关系服从幂律分布,其中,幂律关系式中的幂指数b值不仅为一常数,而且随着应力的增加明显下降,即岩石处于高应力状态时,b值低.例如从中国国家地震局地球物理研究所公布的实验资料(图18)中可看出,岩石破裂实验声发射b值随应力的增加而降低,在达到破裂应力之前b值下降较快[34].

基于b值与地应力相关的原理,由于b值是可以通过历史地震资料统计获得的参数,因此,在水平主应力随埋深分布规律统计回归方程的基础上,可以增加b值作为反映各地地应力状态的信息参量,对现有地应力评估模型进行改进.

图18 5种岩石声发射b值随应力变化图[34]Fig. 18 Change with stress ofthe b-values of acoustic emission from five types of rock [34]

3.3.2 基于b值的川藏交通廊道地应力评估模型

川藏交通廊道穿越印度洋板块俯冲欧亚板块形成的青藏高原,板块边界的作用力是构造变形的主要动力源,同时造成板块内部地震活跃、大地变形、高地应力等现象[35].如图19所示,从青藏高原东缘进藏,需穿越三大缝合带(金沙江缝合带、班公怒江蛇绿岩缝合带、雅鲁藏布江蛇绿岩缝合带)和七大断裂带(龙门山断裂带、鲜水河断裂带、甘孜-理塘断裂带、金沙江-红河断裂带、甲桑卡-赤布张错断裂带、纳木错-仲沙断裂带、嘉黎至然乌断裂带),构造活动较强烈.此外,进藏线路靠近龙门山地震带,穿越甘孜炉霍地震带、雅鲁藏布江地震带,地震烈度均在Ⅷ度以上,地震活动强烈.

以北纬28°～32.1°、东经90.1°～104.1°范围内,1970年1月～2013年12月共45 a的地震资料作为基础数据,震中分布见图20.将地震记录以0.2震级档为间隔进行分级整理.利用Arcgis软件将研究区平面图以0.1°×0.1°的间距进行网格化,挑选出以每个网格节点为圆心、半径为r的圆形统计单元内的地震资料[36],对于多数节点,统计单元的半径r=30 km,但由于地震活动程度存在较大差异,对于地震分布较稀疏的局部区域,统计单元r值可适当扩大,以满足统计所需的地震样本数.对于每一个统计单元,采用非线性拟合方法计算出拟合公式以及拟合优度R2,确定能满足整个研究时段的最小完整性震级Mc[37],不同统计单元的Mc是有差异的,计算中选择拟合优度R2取最大值时对应的震级为Mc.利用最佳拟合优度法,得到最小完整性震级取Mc时的地震活动性参数b值,作为该单元中心点(即网格节点)的计算b值.利用Arcgis软件将得到的整个研究区域扫描计算网格点的b值对离散点进行插值计算,经数值范围和区域颜色的调整后得到b值的空间分布等值线图(图20).由图20可知,b值空间分布沿构造断裂带存在着明显的空间差异,反映出不同断裂带以及同一断裂带不同断裂段现今应力积累水平的差异.川藏交通廊道中，雅安、八美、道孚、甘孜、巴塘至二九六工班、邦达至八宿、通麦、墨竹工卡、曲松等地为异常低b值区,地应力积累水平较高.

图19 川藏交通廊道线路、断裂带、缝合带、中小地震震中分布图Fig. 19 Distribution of lines, faults, sutures, and earthquake epicenters on thetransportation corridor from Sichuan to Tibet

图20 川藏交通廊道b值空间分布Fig. 20 Distribution of b-values of the transportation corridor from Sichuan to Tibet

本文中收集了10个测区,102组地应力原始实测数据.所收集的原始地应力数据测量方法多为钻孔应力解除法和水压致裂法,少数为凯瑟尔效应法.地应力测试工程主要包括:南水北调西线一期工程、二郎山隧道、嘎隆拉隧道、大岗山水电站、两河口水电站等.各测点所在区域的b值见表4.

利用上述资料进行统计回归分析,建立了实测点最大主应力σ1、埋深H、地震b值三者的关系式,即川藏交通廊道地应力评估模型为

σ1=2.270 76-1.417b+0.500 4H.

(19)

利用建模时未使用的硗碛测点、康定测点和墨竹工卡测点的33组实测数据,将式(19)与现有中国陆域八大地块水平主应力评估模型[30]进行对比分析,有24组数据计算值的相对误差比现有模型的相对误差小，表明基于地震活动性参数b值的地应力评估模型精度明显提高.

4 结束语

(1) 基于戴维斯地貌发育理论,按照山地系统的发育阶段,界定了山地系统具备SOC的条件,并提出了基于斯特拉勒积分的山地系统发育阶段判别方法;以地震触发崩塌滑坡作为研究山地系统灾变行为SOC的切入点,对不同地震烈度区地震触发崩塌滑坡的分布规律开展了一项专题研究;介绍了3个SOC在山地系统的应用案例;形成了运用SOC认识和描述山地系统灾变行为的理论架构.

(2) SOC是1987年作为非平衡态统计力学的一个分支建立起来的,对它的现象学研究和对它进行严谨的定义研究仍在进行.SOC已经使人们意识到阈值、亚稳定性、还有大规模波动在一大类多体系统的时空行为中起了决定性的作用,但扰动强度的变化对SOC系统动力学行为特性的影响是尚未有人关注的领域,而自然界,灾变事件的扰动强度变化范围可能会达到几个数量级(如Ⅵ级地震到Ⅸ级地震能量相差达32 768倍).在以汶川地震、芦山地震为原型的研究中,发现随扰动强度增加, SOC系统的动力学特性将经历幂律—幂律弱化—对数正态分布的演变过程.这一有关SOC系统行为演化模式的认识,走出了SOC的传统研究领域,对SOC基础理论的发展也是有力的推动.

(3) 在SOC应用领域的研究尚属初步的工作.通过对SOC系统演化行为模式的深化认识,并与山地灾害实践建立联系,推动山地学从唯象学向精确科学跨越,无疑是具有深远意义的工作.鉴此,本文希望通过范例性的研究产生抛砖引玉之效.

(4) 从科学的实证性来说,相对混沌理论而言, SOC不过分强调系统的演化依赖于系统的初始条件和细节部分,从而更容易分析和实验,沙堆模型的概念似乎可以用来解释从山脉形成到股市波动的几乎所有的事.但若言山地系统的许多独特的细节均可以借助简单的元胞自动机数值模拟来理解,对于多数地理学家而言,可能是不大现实的,同样也受到我们的质疑.例如,自然界中的坡体结构(节理、裂隙面等)都具有非均匀的分布,天然散粒体往往也具有宽级配的特征,因此,组元的非均匀性是山地系统的重要特征之一.但在目前的研究中,未考虑组元非均匀性对其动力学的影响,究其原因主要是尚未开发出能够反映组元非均匀性的元胞自动机模型.因此,考虑通过元胞几何尺寸的非均匀性、排列的随机性、相互作用的各向异性,来构建非均匀元胞自动机模型,探索非均匀性对系统动力学影响的独特细节,揭示山地系统在扰动作用下的深层次灾变规律,将是本团队下一步的主攻方向.

致谢:从散粒体到山地系统灾变行为的SOC,本团队已经过了二十余年的研究历程.先后有十多位教师和研究生参加过该领域的研究工作,对本文直接做出贡献的有郭海强、段书苏、郭沉稳等博士研究生和韩俊硕士研究生等.在此一并深致谢意.

[1] BAK P, TANG C, WIESENFELD K. Self-organized criticality: an explanation of the 1/f noise[J]. Physical Review Letters, 1987, 59(4): 381-384.

[2] HELD G A. Experimental study of critical mass fluctuations in an evolving sand-pile[J]. Physical Review Letters, 1990, 65(9): 1120-1123.

[3] BAK P, TANG C. Earthquakes as a self-organized criticality phenomenon[J]. Geophysical Research, 1989, 97(B11): 15635-15637.

[4] 於崇文. 地质系统的复杂性[M]. 北京:地质出版社,2003: 93-140.

[5] 许强,黄润秋. 岩石破裂过程的自组织临界特征初探[J]. 地质灾害与环境保护,1996,7(1): 25-30.

XU Qiang, HUANG Runqiu. Disscussion on self-organized critical characters in the course of rock failure[J]. Journal of Geological Hazards and Enviroment Preservation, 1996, 7(1): 25-30.

[6] 姚令侃,李仕雄,蒋良潍. 自组织临界性及其在散粒体研究中的应用[J]. 四川大学学报:工程科学版,2003,35(1): 8-14.

YAO Lingkan, LI Shixiong, JIANG Liangwei. Self-organized criticality and its application in granular mixtures[J]. Journal of Sichuan University: Engineering Science Edition, 2003, 35(1): 8-14.

[7] 姚令侃,黄艺丹,杨庆华. 地震触发崩塌滑坡自组织临界性研究[J]. 四川大学学报:工程科学版,2010,42(5): 33-43.

YAO Lingkan, HUANG Yidan, YANG Qinghua. The self-organized criticality of landslids triggered by earthquake[J]. Journal of Sichuan University: Engineering Science Edition, 2010, 42(5): 33-43.

[8] DAVIS W M. The geographical cycle[J]. The Geographical Journal, 1899, 14(5): 481-504.

[9] CHORLEY R J, SCHUMM S A, SUGDEN D E. Geomorphology[M]. London: Methuen & Co. Ltd., 1984: 58.

[10] STRAHLER A N. Hypsometric (area-altitude) analysis of erosional topography[J]. Geological Society of America Bulletin, 1952, 63(11): 1117-1142.

[11] 艾南山. 侵蚀流域系统的信息熵[J]. 水土保持学报,1987(2): 1-8.

AI Nanshan. Comentropy in erosion drainage-system[J]. Journal of Soil and Water Conservation, 1987(2): 1-8.

[12] 吴立新,史文中. 地理信息系统原理与算法[M]. 北京:科学出版社,2003: 441.

[13] 杨景春,李有利. 地貌学原理[M]. 北京:北京大学出版社,2005: 24-26.

[14] 中国科学院青藏高原综合科学考察队. 西藏地貌[M]. 北京:科学出版社,1983: 30-31,200-210.

[15] YAO Lingkan, FANG Duo. On the self-organized criticality of non-uniform sands[J]. International Journal of Sediment Research, 1998, 13(3): 19-24.

[16] BASTIEN C, MICHEL D. 物理系统的元胞自动机模拟[M]. 祝玉学,赵学龙，译. 北京:清华大学出版社,2003: 1-2.

[17] 黄艺丹,姚令侃,郭沉稳. 基于元胞自动机的地震触发崩塌滑坡分布规律[J]. 西南交通大学学报,2013,48(4): 609-615.

HUANG Yidan, YAO Lingkan, GUO Chenwen. Distribution law of landslides triggered by earthquake based on cellular automata[J]. Journal of Southwest Jiaotong University, 2013, 48(4): 609-615.

[18] 胡志旭,姚令侃,王建,等. 面波测试在汶川强震区土体损伤调查中的应用[J]. 防灾减灾工程学报,2010,30(4): 466-470.

HU Zhixu, YAO Lingkan, WANG Jian, et al. Application of surface wave testing in survey of mountain soil damage in Wenchuan strong earthquake area[J]. Journal of Disaster Prevention and Mitigation Engineering, 2010, 30(4): 466-470.

[19] ANG A H-S, TANG W H. 工程规划与设计中的概率概念[M]. 孙芳垂,陈星焘,顾子聪,译. 北京:冶金工业出版社,1991: 268-269.

[20] GUMBEL E J. The statistical theory of extreme values and some practical applications[J]. National Bureau of Standards, 1954, 118(1)： 33.

[21] JOHNSON P A, MCCUEN R H, HROMADKA T V. Magnitude and frequency of debris flows[J]. Journal of Hydrology, 1991, 123: 69-82.

[22] 罗德军,艾南山, 李后强. 泥石流暴发的自组织临界现象[J]. 山地研究,1995,13(4): 213-218.

LUO Dejun, AI Nanshan, LI Houqiang. Breakout of debris flow as a self-organized critical phenomenon[J]. Mountain Research, 1995,13(4): 213-218.

[23] 王裕宜,詹钱登,严璧玉,等. 泥石流体的流变特性与运移特征[M]. 长沙:湖南科学技术出版社,2014: 1-3.

[24] 史道济. 实用极值统计方法[M]. 天津:天津科学技术技出版社,2006: 81-83.

[25] GUMBEL E.J. Statistics of extremes[M]. New York: Columbia University Press, 1958: 269-272.

[26] 张军, 熊刚. 云南蒋家沟泥石流运动观测资料集(1987～1994)[M]. 北京:科学出版社,1997: 1-3.

[27] 吴积善,康志成,田连权,等. 云南蒋家沟泥石流观测研究[M]. 北京:科学出版社,1990: 1-4.

[28] 康志成,崔鹏,韦方强,等. 东川泥石流观测研究站观测实验资料集(1961～1984)[M]. 北京:科学出版社,2006: 1-3.

[29] 景锋,盛谦,张勇惠,等.中国大陆浅层地壳实测地应力分布规律研究[J]. 岩石力学与工程学报,2007,26(10): 2056-2063.

JING Feng, SHENG Qian, ZHANG Yonghui, et al. Research on distribution rule of shallow crustal geostress in China mainland[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 2056-2063.

[30] 杨树新,姚瑞,崔效峰,等. 中国大陆与各活动地块、南北地震带实测应力特征分析[J]. 地球物理学报,2012,55(12): 4207-4217.

YANG Shuxin, YAO Rui, CUI Xiaofeng, et al. Analysis of the characteristics of measured stress in Chinese mainland and its active blocks and North-South seismic belt[J]. Chinese Journal of Geophysics, 2012, 55(12): 4207-4217.

[31] SCHOLZ C H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes[J]. Bulletin of the Seismolo-gical Society of America, 1968, 58: 399-415.

[32] WIEMER S, WYSS M. Mapping the frequency-magnitude distribution in asperities: An improved technique to calculate recurrence times? [J]. Journal of Geophysical Research, 1997, 102(B7): 15115-15128.

[33] WYSS M, SCHORLEMMER D, WIEMER S. Mapping asperities by minima of local recurrence time: San Jacinto-Elsinore fault zones[J]. Journal of Geophysical Research, 2000, 105(B4): 7829-7844.

[34] 李纪汉.b值影响因素的初步研究[J]. 地震学刊,1987(2): 49-53.

LI Jihan. A preliminary study onb-value[J]. Jouranl of Seismology, 1987(2): 49-53.

[35] 姚令侃,邱燕玲,魏永幸. 青藏高原东缘进藏高等级道路面临的挑战[J]. 西南交通大学学报,2012,47(5): 719-734.

YAO Lingkan, QIU Yanling, WEI Yongxing. Challenges in construction of railway and highway from Sichuan to Tibet through eastern margin of Tibetan Plateau[J]. Journal of Southwest Jiaotong University, 2012, 47(5): 719-734.

[36] 易桂喜,闻学泽,范军,等. 由地震活动参数分析安宁河-则木河断裂带的现今活动习性及地震危险性[J]. 地震学报,2004,26(3): 294-303.

YI Guixi, WEN Xueze, FAN Jun, et al. Assessing current faulting behaviors and seismic risk of the Anninghe-Zemuhe fault zone from seismicity parameters[J]. Acta Seismologica Sinica, 2004, 26(3): 294-303.

[37] 刘丽芳,李志海,蒋长胜. 云南地区地震目录最小完整性震级研究[J]. 地震研究,2012,35(4): 491-499.

LIU Lifang, LI Zhihai, JIANG Changsheng. Research on minimum magnitude of completeness for earthquake catalogue in Yunnan region[J]. Journal of Seismological Research, 2012, 35(4): 491-499.

姚令侃(1953—),博士,1996年起至今任职于西南交通大学,现为土木工程学院教授,博士生导师,防灾减灾研究所所长.主要研究方向为铁路公路工程灾害防治及安全技术.获中国科学院科技进步二等奖(1995)、四川省科技进步二等奖(2000)、国家科技进步二等奖(2009)、第十届詹天佑成就奖(2010)、四川省科学技术进步奖一等奖(2013).四川大学兼职教授、中国科学院成都山地灾害与环境研究所所外专家、中国水土保持学会泥石流滑坡专业委员会副主任、铁道部有突出贡献的中青年专家、第三批、第九批四川省学术和技术带头人、享受国务院政府特殊津贴专家.

注:黄艺丹为本文的共同第一作者.

E-mail: yaolk@swjtu.edu.cn

黄艺丹(1982—),博士,2003年起至今任职于西南交通大学,现为土木工程学院讲师.主要研究方向为铁路公路工程灾害防治及安全技术.

E-mail: huangyidan@swjtu.edu.cn

(中文编辑:秦 瑜 英文编辑:兰俊思)

Self-Organized Criticality of Mountain System Catastrophic Behaviors

YAOLingkan1,2,3,HUANGYidan1,2,3

(1. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. MOE Key Laboratory of High-Speed Railway Engineering, Chengdu 610031, China; 3. Road and Railway Engineering Research Institute, Sichuan Key Laboratory of Seismic Engineering and Technology, Chengdu 610031, China)

In order to study the macro-dynamic behavior of mountain systems, a view point was proposed by Davis’s theory of the erosion cycle that valleys in late childhood or mountains in middle adulthood have intrinsic properties of self-organized criticality(SOC). Based on Strahler’s integral, a method for distinguishing landform development stages in a large basin is established. For landslides triggered by earthquake, the data of landslides collected in earthquake zones were analyzed, a cellular automata model was built, and shaking table experiments were performed. As a result, an evolution law of landslides distribution in different seismic intensity zones was revealed. Specifically, there exists a strong negative power-law relationship between the sizes and frequencies of landslides in zones with seismic intensity Ⅶ, Ⅷ and Ⅸ; the relationship becomes a weak power law in zones with seismic intensity Ⅹ, and changes into a lognormal distribution in zones with seismic intensity Ⅺ. Finally, applications of SOC to soil depth assessment under earthquake disturbance, extreme runoff calculation in debris flow control design, and crustal stress evaluation based on the seismic activity parameterb-value, are introduced through three case studies.

mountain system; self-organized criticality(SOC); landslides triggered by earthquake; cellular automata

2015-12-01

国家自然科学基金资助项目(41172321,41571004); 国家重点基础研究发展计划课题(2008CB425802)

姚令侃,黄艺丹. 山地系统灾变行为自组织临界性研究[J]. 西南交通大学学报,2016,51(2): 313-330.

0258-2724(2016)02-0313-18

10.3969/j.issn.0258-2724.2016.02.011

P642

A