迎角/滚转角组合风洞试验中侧向弹性角的影响及处理方法
谢 峰,张 江,秦永明
(中国航天空气动力技术研究院,北京 100074)
迎角/滚转角组合风洞试验中侧向弹性角的影响及处理方法
谢 峰*,张 江,秦永明
(中国航天空气动力技术研究院,北京 100074)
通过迎角/滚转角组合改变模型姿态是横向测力风洞试验中重要的试验方式,此类试验中虽然会提供侧向弹性角数据,但在使用试验数据时往往不使用侧向弹性角数据,这会使得气动载荷与模型姿态对应关系不准确。侧向弹性角由侧向力和偏航力矩引起,在侧向力和偏航力矩较大的试验中,侧向弹性角的影响尤为显著,如方向舵效率试验。本文通过分析侧向弹性角的影响,提出一种侧向弹性角数据处理方法,经试验应用表明可以有效地提高数据使用的准确性。
迎角/滚转角组合;侧向弹性角;数据处理方法
0 引 言
横向试验是风洞试验的重要内容,在飞行器风洞试验中占有很大的比重。常用的横向试验方法有两种[1,2]:1)改变迎角α和侧滑角β组合序列的方法;2)改变迎角α和滚转角γ组合序列的方法,即研究对象为迎角/滚转角组合测力试验,姿态角调节方式具体表现为吹风过程中预置机构滚转角γm,按照序列改变机构迎角αm。其中方法2)比较于方法1)具有堵塞度小的优点,且在大尺寸风洞和小尺寸风洞中都适用,因此在风洞试验中应用十分广泛。
在尾支撑风洞试验中,吹风载荷下天平系统的弹性变形会导致实际姿态角与名义姿态角不同,支杆和天平的弹性形变的角度称为弹性角[1-3]。吹风过程中的实际弹性角由迎角、侧滑角和滚转角三个方向的分量组成,通常利用弹性角校测公式计算得到。在迎角/滚转角组合测力试验中,理想侧滑角保持0°,但实际上由于侧向弹性变形的存在,实际模型的侧滑角并不等于0°,而等于模型的侧向弹性角。当模型所受的侧向力和偏航力矩较大时(如有较大的方向舵偏时),侧向弹性角也会随着增大,成为一个不可忽视的影响量[4-5]。但是,目前风洞的迎角/滚转角组合测力试验中仅仅是提供侧向弹性角数据,并没有对其影响进行修正,往往在使用气动数据时,将侧滑弹性角当做小量忽略。使用未考虑侧向弹性角影响的迎角/滚转角组合描述模型姿态角,会使得气动载荷与模型姿态对应关系不准确,必然会导致试验数据误差的增大,特别是对侧向力系数和偏航力矩系数的精准度影响明显。
本文针对迎角/滚转角组合风洞试验数据的侧向弹性角数据处理问题,通过分析侧向弹性角的影响,说明侧向弹性角数据处理在高精度测力试验中,以及在模型侧滑角较大和方向舵偏较大的状态下不容忽视,进而提出消除侧向弹性角得到等效迎角/滚转角组合的方法,并以方向舵效率试验为例,表明这种方法的必要性和有效性。
1 侧向弹性角及其计算和影响
天平杆在承受气动力和气动力矩作用时会产生弹性变形,使安装在天平上的模型姿态发生变化,迎角变化Δαe,侧滑角变化Δβe,滚转角变化Δγe。Δαe、Δβe和Δγe分别称为纵向弹性角、侧向弹性角和横向弹性角[6-7]。
当天平杆受到的气动力和气动力矩不超过一定的限度时,弹性角随对应气动力和气动力矩基本呈现线性变化关系。由公式(1)可以导出弹性角。

式中:Mz、y、My、z和Mx分别为天平承受的俯仰力矩、法向力、偏航力矩、侧向力和滚转力矩。系数可以通过天平杆地面静校得到。
在某迎角/滚转角组合风洞试验中,模型预转滚转角从0°到90°,中间间隔5°,选取机构迎角αm= 15°,观察侧向弹性角Δβe随机构滚转角γm的变化,如图1所示。
常规测力试验的角度精度要求不超过±0.05°,国外先进水平的角度精度要求不超过±0.005°。从图1及其数据可以得知侧向弹性角Δβe最大可达0.17°,如果不对侧向弹性角数据进行处理,将对数据使用的准确性带来较大影响。
以往的迎角/滚转角组合风洞试验中因侧滑弹性角较小、影响较小且处理困难等原因,在使用数据时不加以考虑侧向弹性角。然而在高精度测力试验[8]中侧向弹性角的影响不可忽略,而且目前许多飞行器需要测量大侧滑角、大方向舵偏状态下的气动数据,侧向弹性角的影响更加不容忽视。迎角/滚转角组合风洞试验中在使用数据时侧滑弹性角的影响具体表现为:未考虑侧向弹性角Δβe影响的模型迎角/滚转角组合姿态与准确的模型迎角/滚转角组合姿态有较大的不同,从而带来气动特性偏差。

图1 侧向弹性角随机构滚转角的变化Fig.1 Lateral flexible angle change corresponds to roll angle of machanisms
2 侧向弹性角Δβe的数据处理方法
在迎角/滚转角组合测力试验中,机构迎角为αm,机构滚转角为γm,弹性角变形分别为Δαe、Δβe和Δγe,那么模型的姿态角可以表达为:

在使用数据时,若忽略侧向弹性角Δβe数据,则模型姿态角表达为
下面提出一种侧向弹性角Δβe的数据处理方法,其目标是消除侧向弹性角得到准确表达模型姿态的等效迎角/滚转角组合[9]。首先结合风洞坐标系和模型坐标系定义一个空间坐标系,然后基于风洞坐标系与模型坐标系之间的转换关系以及空间坐标系与模型坐标系之间的转换关系,推导出考虑侧向弹性角Δβe影响后的等效模型迎角/滚转角组合。
2.1 轴系定义
风洞坐标系O-xwywzw的原点位于导弹的质心,Oxw轴始终指向导弹的空速方向;Oyw位于包含Oxw轴的铅垂平面内,垂直于Oxw轴,指向上;Ozw轴垂直于Oxwyw平面,其方向按照右手直角坐标系确定。坐标轴对应的单位矢量分别为Oxw、Oyw和Ozw。
模型坐标系O-xbybzb的原点位于导弹的质心,Oxb始终指向导弹的弹体轴线方向,指向前;Oyb轴在弹体的纵向对称面内,垂直于Oxb轴,指向上;Ozb轴垂直于弹体纵向对称面,其方向按照右手直角坐标系确定。坐标轴对应的单位矢量分别为Oxb、Oyb和Ozb。
空间坐标系O-xsyszs的原点位于导弹的质心,Oxs轴始终指向导弹的空速方向;Oys位于Oxs轴和Oxb轴所在的平面内,垂直于Oxs轴,指向上;Ozs轴垂直于Oxsys平面,其方向按照右手直角坐标系确定。坐标轴对应的单位矢量分别为Oxs、Oys和Ozs。
2.2 轴系转换
以风洞坐标系为基准,依次转过αa角、βa角和γa角,得到模型坐标系的姿态(如图2所示)。两坐标轴之间的转换关系应有[10]:
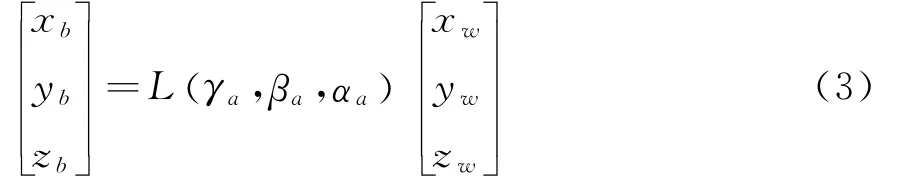
式中:

以空间坐标系为基准,依次转过αeq角和γeq角,得到模型坐标系的姿态(如图3所示)。两坐标轴之间的转换关系应有:
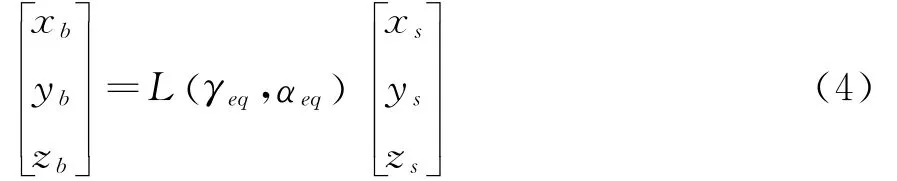

图2 风洞坐标系与模型坐标系转化关系图Fig.2 Relationship of wind tunnel coordinate and model coordinate

图3 空间坐标系与模型坐标系转化关系图Fig.3 Relationship of space coordinate and model coordinate
式中:
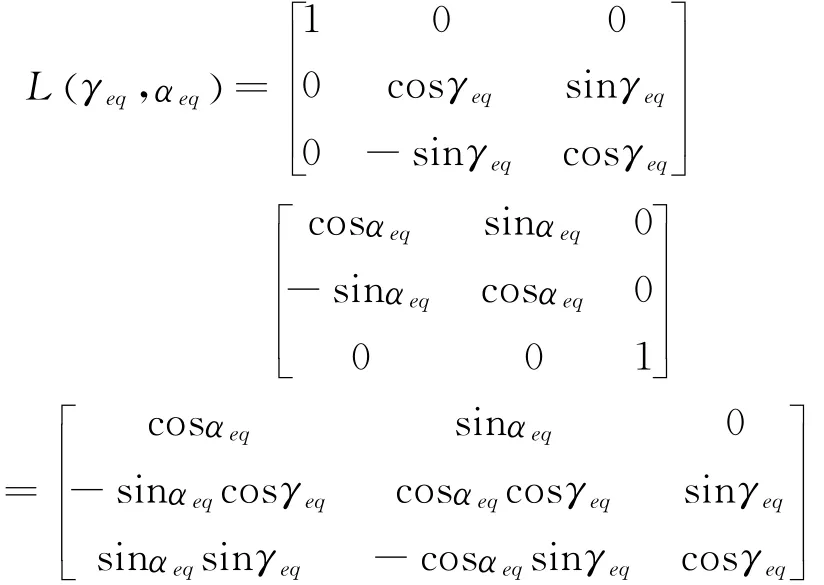
2.3 等效迎角/滚转角组合公式
由坐标系定义可知,Oxw与Oxs为同一矢量,因此方向余弦〈Oxb,Oxw〉=〈Oxb,Oxs〉,〈Oyb,Oxw〉=〈Oyb,Oxs〉,〈Ozb,Oxw〉=〈Ozb,Oxs〉,展开得如下三个关系式:
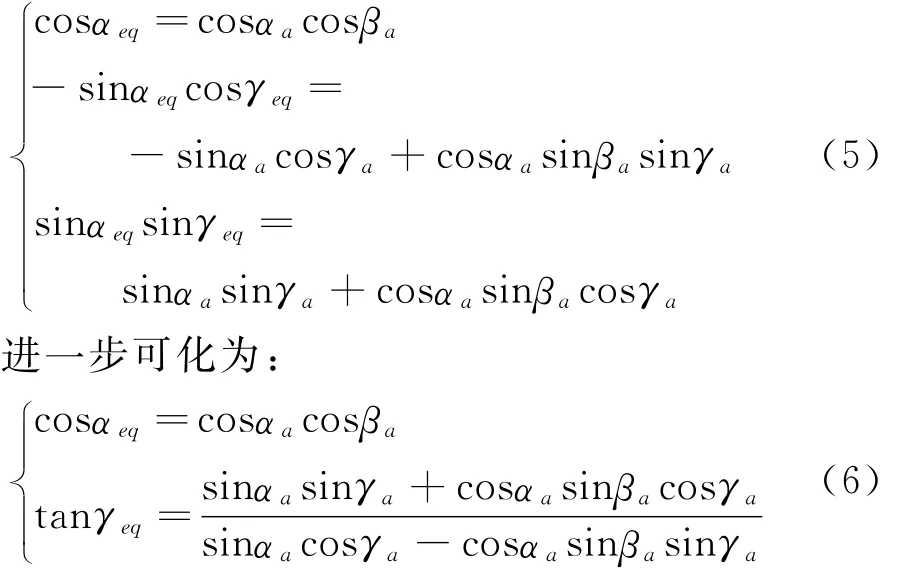
从公式中可以看出当αa接近于0°时,tanγeq≈近似互余关系,γeq与γa差别很大,使滚转角γeq序列不连续,给使用数据带来不便。又因为在迎角/滚转角组合测力试验中,零机构迎角状态下的气动载荷非常小,不同的滚转角之间不会有很大的气动载荷变化,从而侧向弹性角也非常小,其影响可以忽略不计,所以对零机构迎角状态的情况可以不考虑侧向弹性角影响。
2.4 侧向弹性角对迎角和滚转角的影响根据算例试验数据,分别计算得到组合与组合,对比结果如图4所示。
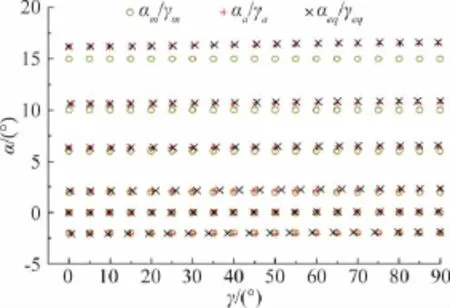
图4 不同姿态角组合的对比结果Fig.4 Compare of different attitude angle combination
选取机构迎角αm=15°时,(αa,βa,γa)与(αeq,βeq,γeq)的对比数据如表1所示。
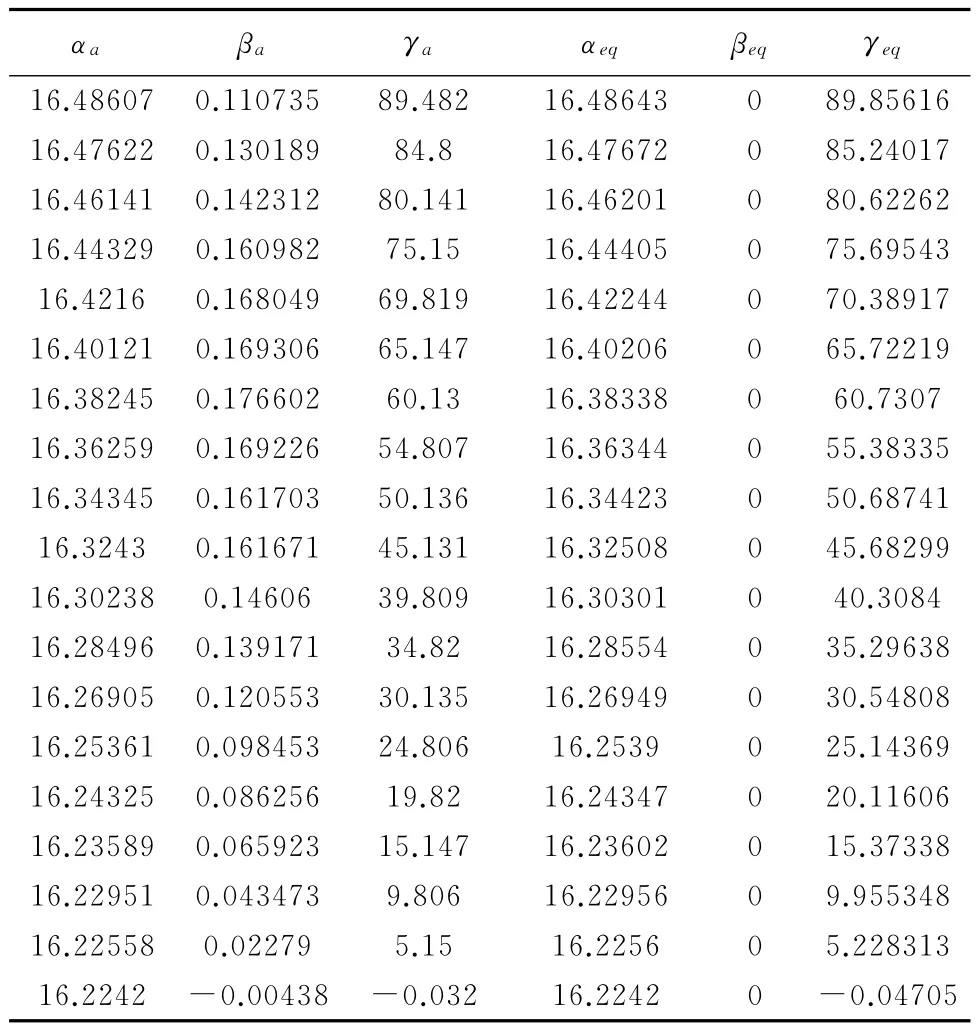
表1 (αa,βa,γa)与(αeq,βeq,γeq)的对比数据Table 1 Compare between(αa,βa,γa)and(αeq,βeq,γeq)
从图及其表可以得知,αa与αeq相比差别较小,γa与γeq相比差别较大,在机构迎角αm=15°时αa与αeq相差0.0005°左右,γa与γeq相差可达0.5°。因此侧向弹性角Δβe对模型迎角影响可以忽略不计,对模型滚转角带来的影响较大。
2.5 侧向弹性角对侧向力和偏航力矩的影响
下面分析侧向弹性角对侧向力和偏航力矩的影响。在迎角-滚转角组合测力试验中,风洞坐标下的气动力和气动力矩需要转换到模型坐标系下的气动力和气动力矩。将气动力和气动力矩转换到模型坐标系的公式如下:
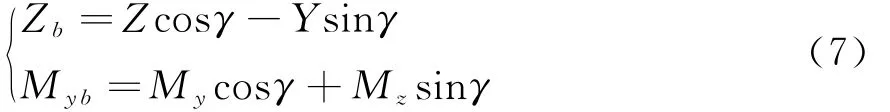
其中,Zb和Myb为模型坐标系下的侧向力和偏航力矩,Z、Y、My和Mz分别为天平测得的侧向力、法向力、偏航力矩和俯仰力矩。γ在这里根据是否考虑侧向弹性角Δβe影响,分别表现为γeq与γa。
机构迎角αm为15°,模型滚转角变化范围为[0°,90°]的情况下,侧向弹性角对模型坐标系下的侧向力和偏航力矩的影响如图5和图6所示。

图5 侧向弹性角对侧向力的影响Fig.5 Lateral flexible angle influence on lateral force

图6 侧向弹性角对偏航力矩的影响Fig.6 Lateral flexible angle influence on yawing moment
从 图 中 可 以 看 出,在 γ ∈ (0°,20°)∪(70°,90°)时,侧向弹性角Δβe对侧向力系数Czb和偏航力矩系数myb的影响较小,在时,侧向弹性角Δβe会对Czb产生0.018左右的修正量,约占Czbmax的10%,并且对myb产生0.015左右的修正量,约占mybmax的4%,在要求高精度试验数据时必须考虑Δβe的影响。
3 应用示例-导弹方向舵效率试验
着方向舵偏角的增大而增大,随迎角的变化近似呈现点对称分布,且在迎角-5°时达到最大值,最大值分别为0.238和0.076。
通过计算ΔCz与方向舵效率的比值可以得到ΔCz的等效方向舵偏角,计算Δmy与方向舵效率的比值可以得到Δm的等效方向y
导弹方向舵效率试验[2]若采用迎角/滚转角组合测力方式,侧向力和偏航力矩较大,可能会带来较大的侧向弹性变形,侧向弹性角的数据处理对导弹气动特性的影响较大。以某导弹测力试验为例,Ma=0.9,机构滚转角γ=45°,模型迎角α序列[-15°,-10°,-5°,0°,5°,10°,15°],方向舵偏角δ序列[-25°,-12.5°,0°,12.5°,25°],侧向弹性角Δβe对模型滚转角的影响量为Δγ(Δγ=γeq-γa),Δγ随迎角和方向舵偏角的变化曲线如图7所示。舵偏角,如表2和表3所示。
从表中可以得知,在舵偏角δ=-25°,迎角α=-5°时,ΔCz和Δmy的等效方向舵偏角在2°左右。这在方向舵效率试验中为不可忽略的偏差,因此考虑侧向弹性角Δβe影响对迎角/滚转角组合进行修正是不可忽略的数据处理步骤。

图7 Δγ随迎角和方向舵偏角的变化曲线Fig.7 Δγversus angle of attack and angle of rudder

图8 ΔCz随迎角和方向舵偏的变化曲线Fig.8 ΔCzversus angle of attack and angle of rudder
从图中可以看出,Δγ在正负迎角范围内变化近似关于原点呈点对称分布,分别在α=±5°时绝对值达到极大。与此同时,舵偏量越大,Δγ越大。在此试验中,δ=-25°,α=5°,Δγ达到最大值3.87°,可见比无方向舵偏情况下对模型滚转角数据造成更大的影响。
考虑侧向弹性角Δβe影响的情况下,模型坐标系下的侧向力系数Cz与偏航力矩系数my的影响量分别为ΔCz与Δmy。ΔCz与Δmy随迎角和方向舵偏的变化曲线如图8和图9所示。
从图8和图9中可以看出,ΔCz与Δmy基本上随

图9 Δmy随迎角和方向舵偏的变化曲线Fig.9 Δmyversus angle of attack and angle of rudder

表2 ΔCz的等效方向舵偏角Table 2 Equivalent rudder angle ofΔCz

表3 Δmy的等效方向舵偏角Table 3 Equivalent rudder angle ofΔmy
4 结 论
通过迎角/滚转角组合改变模型姿态是重要的横向测力风洞试验方式。本文分析侧向弹性角的影响,并且通过定义一个空间坐标系,建立了模型姿态(αa,βa,γa)与模型姿态(αeq,γeq)之间的关系式,给出了侧向弹性角数据处理方法。通过计算及试验得到如下结论:
(1)侧向弹性角对模型迎角影响不大,对模型滚转角影响较大;
(2)在一定机构滚转角范围内,侧向弹性角对模型坐标系下的侧向力和偏航力矩影响较大;
(3)在方向舵效率试验中,侧向力和偏航力矩较大,从而侧向弹性角较大,侧向弹性角对模型滚转角、侧向力和偏航力矩的影响更为显著。侧向弹性角引起的ΔCz和Δmy的等效舵偏角在方向舵效率试验中为不可忽略的偏差。
(4)本文给出的侧向弹性角处理方法,能够得到准确表达模型姿态的等效迎角/滚转角组合,提高试验数据的使用准确性。
[1] 范洁川.风洞试验手册[M].北京:航空工业出版社,2002.
[2] 恽起麟.实验空气动力学[M].北京:国防工业出版社,1991.
[3] 恽起麟.风洞试验[M].北京:国防工业出版社,2000.
[4] Goether B H.Transonic Wind Tunnel Testing[M].1961.
[5] 王文正.基于数学模型的气动力数据融合研究[J].空气动力学报,2009,27(5):524-528.
[6] 王铁城.空气动力学实验技术[M].北京:航空工业出版社,1995.
[7] 贺德馨.风洞天平[M].北京:国防工业出版社,2001.
[8] GJB 1061-1991高速风洞和低速风洞测力试验精度指标[S].
[9] S.Tavoularis.Equivalence between sideslip and roll in wind-tunnel model testing[J].J.Aircraft,2012,36(5):895-896.
[10]方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2005.
The effect and processing method for the lateral flexible angle in the angle of attack and roll coupled wind tunnel test
Xie Feng,Zhang Jiang,Qin Yongming
(China Academy of Aerospace Aerodynamics,Beijing 100074,China)
Changing the model attitude with the coupled angle of attack and roll is an important mode for the lateral test.Although the lateral flexible angle is offered in this kind of test,the data of lateral flexible angle is often neglected,which leads to the inaccuracy of the relation between the aerodynamic loads and the model attitude.Lateral flexible angle is generated from the lateral force and the yawing moment,and the effect of the lateral flexible angle will be notable when the values of the lateral force and the yawing moment are large in the test,for example,the yaw steerage test.The effect of the lateral flexible angle is analyzed,offers a data processing method of the lateral flexible angle.Calculative and experimental results show that the method can increase the accuracy of the application data.
the angle of attack and roll coupled;the lateral flexible angle;a data processing method
V211.7
Adoi:10.7638/kqdlxxb-2015.0115
0258-1825(2016)01-0027-06
2015-07-21;
2015-09-09
国家自然科学基金(11302214)
谢峰(1988-),男,福建福州人,助理工程师,硕士,研究方向:飞行力学.E-mail:xiefeng11112@163.com
张江(1978-),男,博士,高级工程师,研究方向:实验空气动力学.E-mail:13611319903@163.com
谢峰,张江,秦永明.迎角/滚转角组合风洞试验中侧向弹性角的影响及处理方法[J].空气动力学学报,2016,34(1):27-32.
10.7638/kqdlxxb-2015. Xie F,Zhang J,Qin Y M,et al.The effect and processing method for the lateral flexible angle in the angle of attack and roll coupled wind tunnel test[J].Acta Aerodynamica Sinica,2016,34(1):27-32.

