基于三维数字图像相关法（DICM）的输电导线风致动态位移测试及分析

王述良，梁枢果，邹良浩，杨 威，吴 鹏

（武汉大学土木建筑工程学院，湖北武汉 430072）

基于三维数字图像相关法（DICM）的输电导线风致动态位移测试及分析

王述良，梁枢果＊，邹良浩，杨 威，吴 鹏

（武汉大学土木建筑工程学院，湖北武汉 430072）

基于三维DICM的非接触位移测试技术对导线气弹模型沿跨位移时程进行了测试，并对其进行统计与频谱分析，得到了导线风致位移的变化规律与概率分布特性。分析结果表明：导线在风荷载作用下，水平向振动表现为以一阶面外振型为主导、面内亦有一定贡献的振动形式，且随着风速的增加，面内振型的贡献也相应提高，从而使得导线在高风速下的面内振型的贡献不可忽略；对于竖向振动而言，其主导振型为面外一阶以及面内对称一、二阶；总体而言，在考虑导线风致响应时，选择包含面外一阶、面内一、二阶对称振型在内的三阶振型能够较为精确地反映其风致振动的主要能量组成；随着风速的增加，输电线面内、外非线性耦合程度增强，其风致响应不再满足高斯分布，位移响应峰因子应作相应调整。

三维DICM技术；输电导线；风洞试验；气弹模型；位移测试

0 引 言

输电导线是输电塔－线体系的重要组成部分，其大跨、高柔的结构特性使得其在风荷载作用下发生大幅振动，由此引起的动张力可能导致塔体和连接构件的损坏，以至于影响整个线路的正常运行。然而，目前对输电导线风致振动的研究主要集中在理论层面［1］，其合理性有待现场实测［2］或风洞试验［3］的验证。针对导线风洞试验而言，导线敷冰舞动机理及其气动特性是既有研究的重点［4－5］。实测结果［6］表明：引起导线大幅振动的因素除了极端气候条件下的舞动以外，常规气候条件下抖振引起的输电线路构件的疲劳破坏也不可忽视。在风荷载作用下，由于来流湍流引起的导线振动表现出其面内、外振型耦合的复杂动力特性及气动特性。

为了了解导线的风致振动机理及气弹效应，基于气弹模型风洞试验的位移测试是一种重要手段。然而，导线这样的柔性悬索结构，在风荷载作用下表现为三维强非线性振动形式，且其细长的结构特性，使得位移测试相当困难，尽管目前针对位移测试所采用的常规接触式［7］和非接触式［8］技术已经非常成熟，但针对导线位移的测试却存在以下不足：1）接触式位移测试技术会给测试对象引入附加条件而产生测试误差，尤其对导线而言这种误差将会更为显著；2）尽管相对于常规的物理、机械式位移测试技术，激光位移计避免了接触式位移测试技术所产生的误差，但其在位移测试中受到多种条件的限制：需要足够的反射面才能捕捉和反射入射激光；激光强度和电子元件阈值的限制使得激光布置的范围受限，其离结构表面的距离不可太近或太远；仅限于一维单点位移的测试。针对既有接触式、非接触式位移测试技术的缺陷，学者已开展了基于数字图像相关方法［9－10］（Digital image correlation method，DICM），采用光学相机采集的图像结合后期处理的全局化、自动化位移测试技术的研究，在工程中也得以广泛应用［11－13］。然而，传统的基于单摄像机的二维DICM，只能测量结构表面的面内位移［12］。

鉴于此，本文进行了导线全跨气弹模型风洞试验，并采用基于双目视觉的三维DICM测试技术对导线沿跨多点位移进行了测试，该技术基于双目立体视觉原理实现了导线风致三维位移的捕捉。在试验数据的基础上分析了导线风致位移响应的一般变化规律，并初步分析了导线的风致振动机理以及导线风致位移响应的概率分布，以期为导线风致响应的计算提供一定参考。

1 立体视觉测量基本原理

立体双目视觉由左右两部摄像机组成，基于视差原理实现三维动态位移的测试。图1所示为简单的平视双目立体成像原理图，两摄像机的投影中心连线的距离，即基线距为b。摄像机坐标系原点在摄像机镜头的光心处，坐标系如图1所示。事实上摄像机的成像平面在镜头的光心后，图1中将左右成像平面绘制在镜头的光心前f处，这个虚拟的图像平面坐标系O1的u轴和v轴与和摄像机坐标系的x轴和y轴方向一致，这样可以简化计算过程。左右图像坐标系的原点在摄像机光轴与平面的交点O1和O2。空间中某点P在左图像和右图像中相应的坐标分别为P1（u1，v1）和P2（u2，v2）。

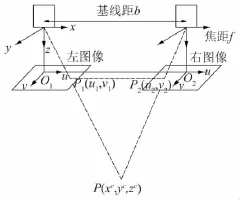
图1 双目立体视觉成像原理图Fig.1 Schematic of image formation based on binocular vision

假定两摄像机的图像在同一个平面上，则点P图像标的Y坐标相同，即v1＝v2。由三角几何关系得到：

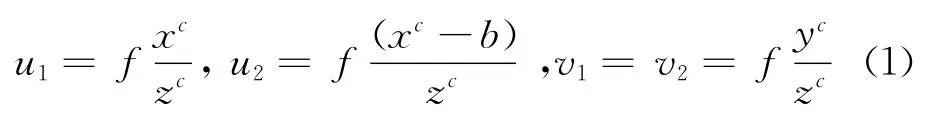
式中，（xc，yc，zc）为点P在左摄像机坐标系中的坐标，b为基线距，f为两个摄像机的焦距，（u1，v1）和（u2，v2）分别为点P在左图像和右图像中的坐标。视差定义为某一点在两幅图像中相应点的位置差：

由此可计算出空间中某点P在左摄像机坐标系中的坐标为：

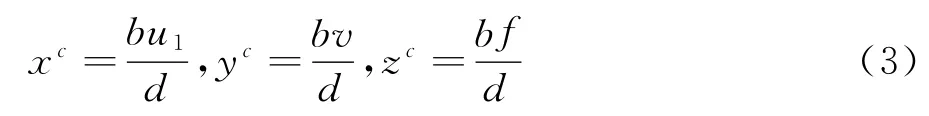
因此，只要能够找到空间中某点在左右两个摄像机像面上的相应点，并且通过摄像机标定获得摄像机的内外参数，就可以确定这个点的三维坐标。

2 风洞试验

2.1 气弹模型设计与制作

本次试验以实际JL／G3A－1000／45型号特高压输电线为蓝本，设计并精细制作了六分裂输电线气弹模型，该型号单根导线截面直径42.08mm，线密度3100kg／km，弹性模量60.6GPa。导线档距500m，悬挂高度75m，垂度17.5m，分裂间距500mm。

根据相似理论，按照几何缩尺比λL＝1∶25制作了满足几何相似及质量、阻尼、弗劳德数、斯托罗哈数和柯西数等气动参数的输电导线气弹模型，其制作方法为：采用铜丝模拟导线的刚度，塑料管模拟导线的外形，分段包于铜丝之外，不提供输电线模型的拉伸刚度。铅丝紧密缠绕于塑料管表面提供附加质量以模拟输电线的线密度。同时，作为增加由于塑料管材料截面的限制造成的迎风面积的不足。使用1mm厚ABS板模拟六分裂输电线间隔棒，其质量相对于输电线本身而言可以忽略。

2.2 风洞试验设备与方法

输电导线气弹模型风洞试验在西南交通大学XNJD－3号风洞中进行，该风洞为立式回流闭口式边界层风洞，试验段截面宽22.5m，高4.5m，长36m。试验风速范围为1m／s至16.5m／s连续可调。试验时，采用多个尖劈和分布立方体粗糙元模拟输电塔－线体系B类典型地貌湍流风场，如图2所示。试验风速2～7m／s。风洞试验照片如图3所示。图4为经处理之后的导线灰度图，其中Tap3～Tap0分别为跨中及距离为2m的四个测点。位移数据采样频率40Hz，采样时间40s，尽管采样频率只有40Hz，但由于输电导线的卓越频率相对较低，也足以涵盖其风致振动的主要信息。

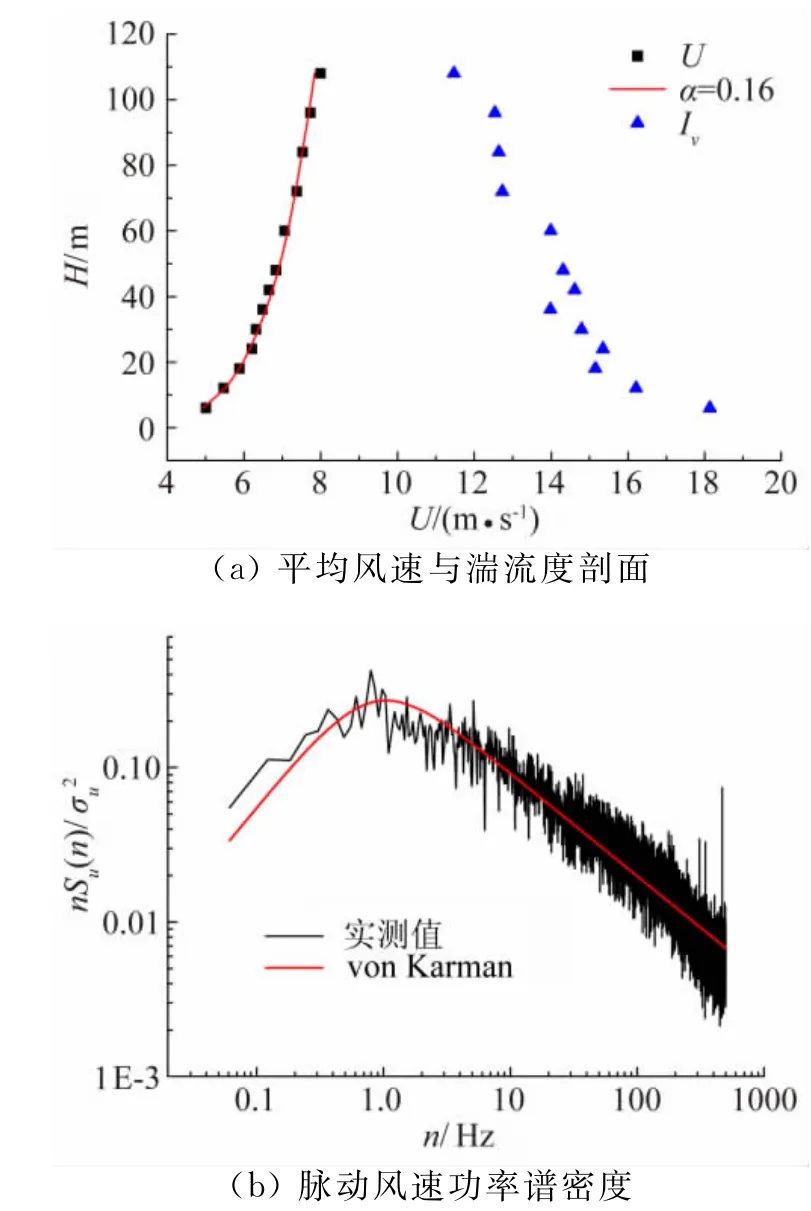
图2 风场模拟Fig.2 Wind field simulation

图3 风洞试验位移测试Fig.3 Displacements measurement of transmission line in wind tunnel

图4 图像处理及测点捕捉Fig.4 Image capturing and processing of measuring taps

3 动力特性

根据悬索理论［14］，可以求得本次试验导线模型振型频率的理论解，如表1所示。

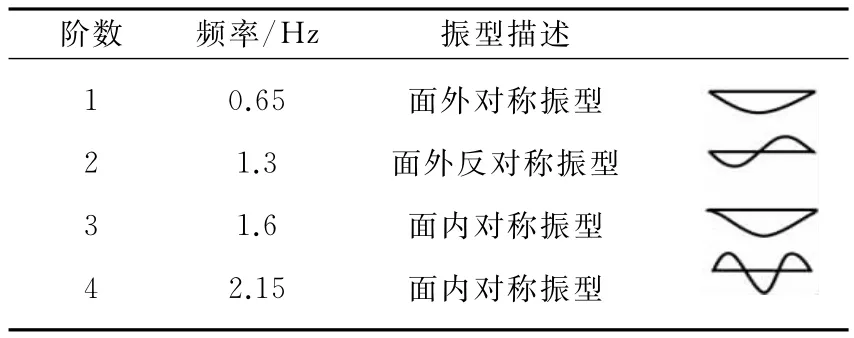
表1 导线模型前四阶振型频率Table 1 Frequencies of the first four modes of transmission line model

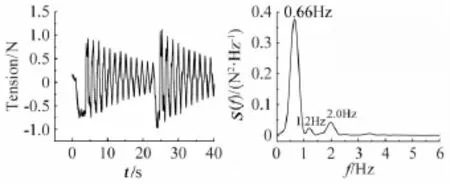
图5 自由振动下导线平面外张力时程及功率谱Fig.5 Time history and PSD of out－of－plane tension of transmission line

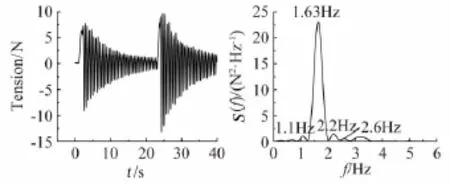
图6 自由振动下导线平面内张力时程及功率谱Fig.6 Time history and PSD of in－plane tension of transmission line

为了验证输电导线气弹模型制作的效果，对导线模型进行了自由振动响应的测试，采用测力天平测得的张力进行频率识别。图5和图6给出了导线自由振动平面内、平面外动张力时程以及对应的功率谱密度函数。由图可以看出导线模型面外一阶对称振型频率实测值为0.66Hz与目标值比较接近，竖向激发出面内一阶对称振型，其频率为1.63Hz与目标值也比较接近，验证了本文模型制作的可靠性。

4 试验结果及分析

4.1 试验测试结果

双摄像机采集到振动过程中导线各瞬时的位置，并对图像进行初步的灰度处理以便识别测点标识，通过数字图像相关法，搜索并捕捉各测点并计算其坐标，再根据相机的基本参数，识别出导线各测点的位移时间历程。由于位移数据通过图像处理完成，因此在处理过程中由于导线在大风速下发生大风偏角振动，测点标识会出现一定的倾斜，导致相机难以准确捕捉其位置，因此会产生数据点遗失的问题。数据点遗失率与导线平均风偏角的关系如图7所示。可知，随着风速的增加导线风偏角增大，测点Tap1和Tap3的遗失率会急剧增加，但Tap2数据样本完好。因此除了测点标识的倾角外，测点位置对相机测量精度也有很大影响。但总体而言，整个数据样本点的遗失率均控制在6%以内，能够满足导线在强风作用下的位移响应测量。

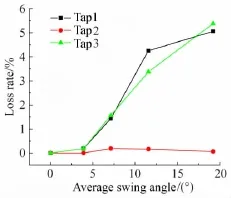
图7 位移测试采样数据点遗失率Fig.7 Loss rates of displacement sampling data

图8给出了5m／s时导线跨中测点Tap3的水平向（Horizontal）、竖向（Vertical）以及弦向（Chordwise）三个方向的位移风致位移响应时程。初步可以看出导线水平向振动较为明显，同时发生与竖向的耦合振动，但弦向位移较小，且在实际输电塔线体系中往往由于多跨的存在使得弦向振动相互抵消，因此在进行响应计算及分析时不予考虑。对比不同测点的水平向位移时程可知，导线跨中位移最大，离跨中越远位移响应越小。

4.2 位移响应统计分析图9给了导线跨中水平向、竖向以及弦向平均及均方根位移随风速的变化情况。由图可知，导线水平向位移较竖向位移大得多，实际风速35m／s时候，平均位移可达近10m。对于竖向平均位移而言，低风速下位移很小，高风速时位移增加也比较显著，实际风速35m／s时，位移亦可达到1.25m。随着风速的增加各个方向位移响应差异会更为明显。

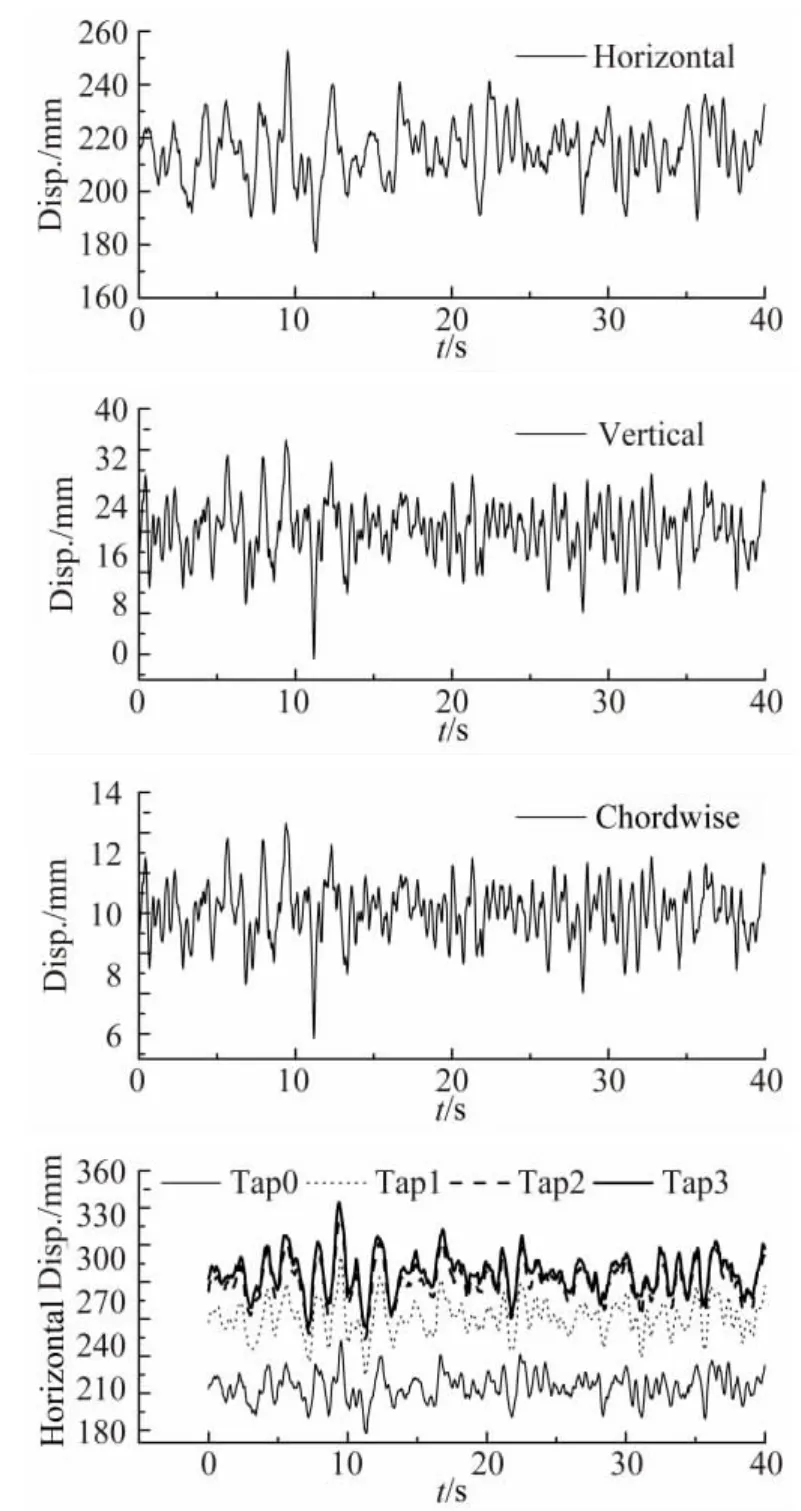
图8 导线位移时程Fig.8 Time history of transmission line displacements

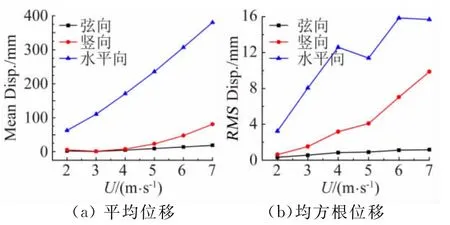
图9 导线位移响应Fig.9 Displacement responses of transmission line

根据水平向位移和弧垂可以确定导线平均风偏角。需要指出的是，尽管导线在风荷载作用下由于附加张力的存在使得导线有一定的拉伸，但其幅度不足以引起导线在平均风偏位置弧垂的较大变化。因此，在计算平均风偏角时，弧垂取初始构形的弧垂。图10给出了不同测点平均风偏角随风风速的变化情况。可知，导线各测点平均风偏角一致，说明导线在平均风偏位置的构形仍然处于同一平面。因此，从风洞试验的角度看，导线的风致振动可以分为包括自重状态的初始构形、平均风荷载作用下的平均风偏构形以及平均风偏位置的脉动这三个状态，这一点与理论模型［15］是一致的，三种状态的力学分析坐标系和简图如图11所示。

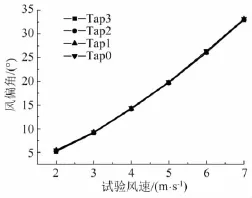
图10 导线各测点平均风偏角Fig.10 Average swing angles

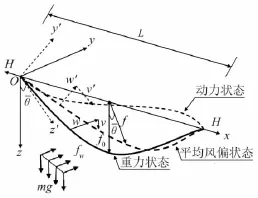
图11 空间导线的动态构形Fig.11 Dynamic configuration

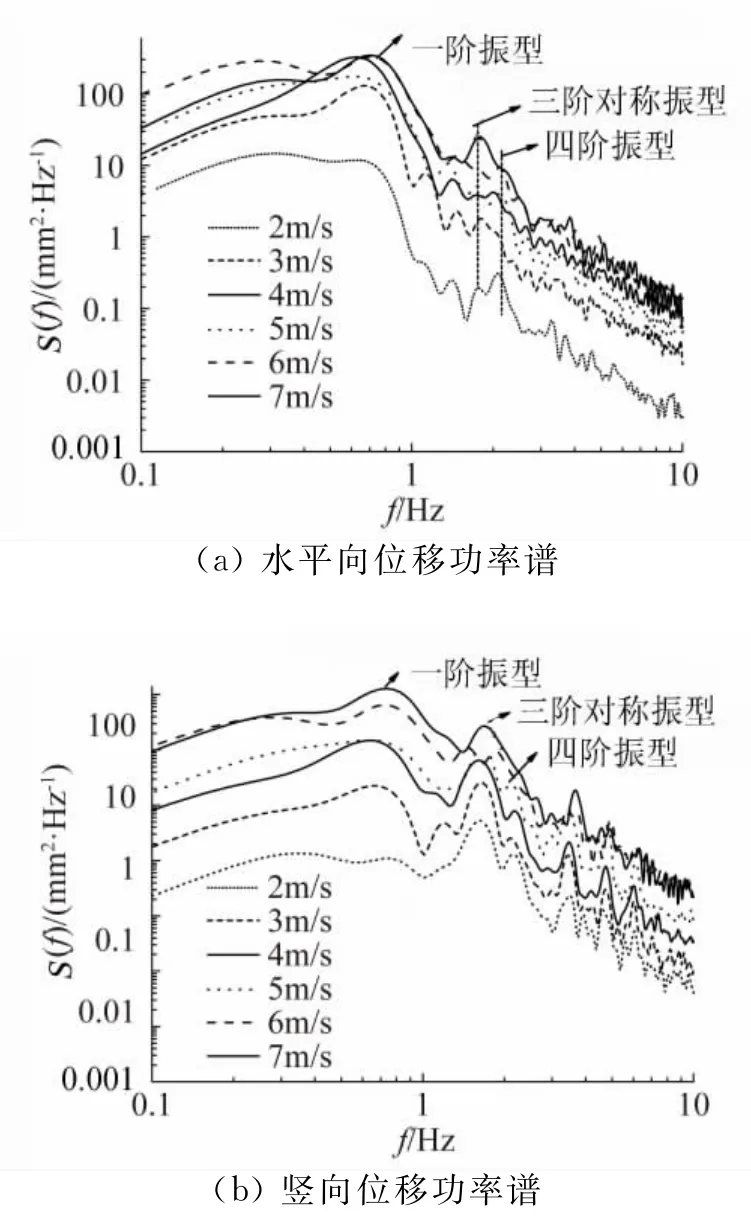
图12 导线跨中位移响应功率谱Fig.12 PSDs of displacement of intermediate measuring tap

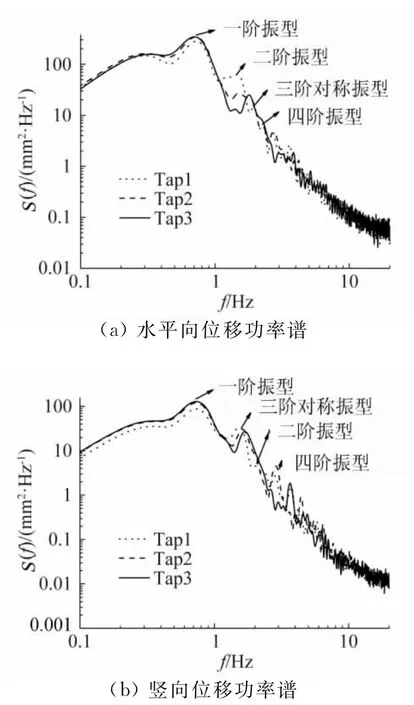
图13 导线跨不同位置位移响应功率谱Fig.13 PSDs of displacement of different measuring taps

4.3 位移响应频谱分析

根据导线位移时程可以计算得到位移功率谱密度函数。图12（a）和（b）给出了不同风速下导线跨中测点的水平向、竖向位移功率谱，由图可以看出：导线水平位移响应功率谱的成分相对单一，其主导频率为导线的平面外一阶对称振型频率，但随着风速的增加面内一、二阶对称振型频率亦有一定的贡献，总体而言并不显著。对于竖向位移功率谱而言，面内、面外一阶对称振型频率占主导地位，随着风速的增加高阶振型的贡献不可忽略。因此，在进行导线风致响应计算分析时取导线面外对称一阶、面内对称一阶以及面内对称二阶振型是合理的。

图13（a）和（b）分别给出了试验风速7m／s时导线沿跨不同测点水平向和竖向位移响应功率，可以看出：对于水平向位移功率谱而言，各测点频率分布特性类似，但需要指出的是，导线的反对称振型在非跨中的位置有所显现，而跨中位移响应谱中二阶反对称振型频率没有明显的峰值，其原因是反对称振型在跨中位置出现奇点。与水平向位移功率谱不同的是，竖向位移功率谱除了主导频率有所不同以外，不同测点低频能量会有所差异，除此之外，离跨中位置越远的测点其面内一阶振型频率的贡献越大，而二阶对称振型频率则刚好相反。同样，在出现跨中奇点的反对称振型频率有明显峰值的测点不包含在跨中位置的测点位移响应谱中。

4.4 位移响应概率分布特性分析

图14给出了导线竖向和水平向位移响应的概率分布与高斯分布的对比情况，从图可以看出，试验风速2m／s时，导线竖向与水平向位移响应实际概率分布与高斯分布存在较大差异，呈现出一种“双峰”分布形式，整体而言表现为一种更宽的分布特性。而对于试验风速4m／s时，响应的实际分布与高斯分布比较吻合。高风速时，尽管响应的实际分布形式类似于高斯分布，但表现为一种“尖而窄”的单峰分布形式。其原因在于：导线在低风速下的振动由来流湍流引起，来流湍流的高斯分布特性决定着其响应的分布特性，随着风速的增加，导线面内、外非线性耦合作用的增强，使得其响应分布特性发生改变。

通常情况下，风荷载服从高斯分布，确定性结构在其作用下的响应也应服从高斯分布。因此，在保证率为99.73%的情况下，峰因子的取值为3。但实际上，从导线位移响应峰因子（如图15所示）可以看出：如果按照高斯分布来考虑导线的风致响应，低风速时会高估其极值响应，以此作为参考进行结构设计会偏于安全；而高风速时，又会低估其极值响应，因此取峰因子为3会使得导线的结构设计偏于危险。故在进行导线风致极值响应分析时，高风速下其峰因子应该适当的提高。

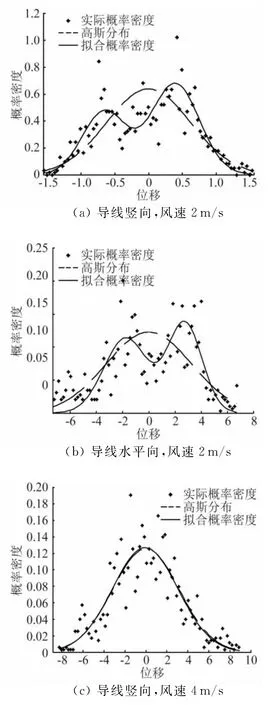
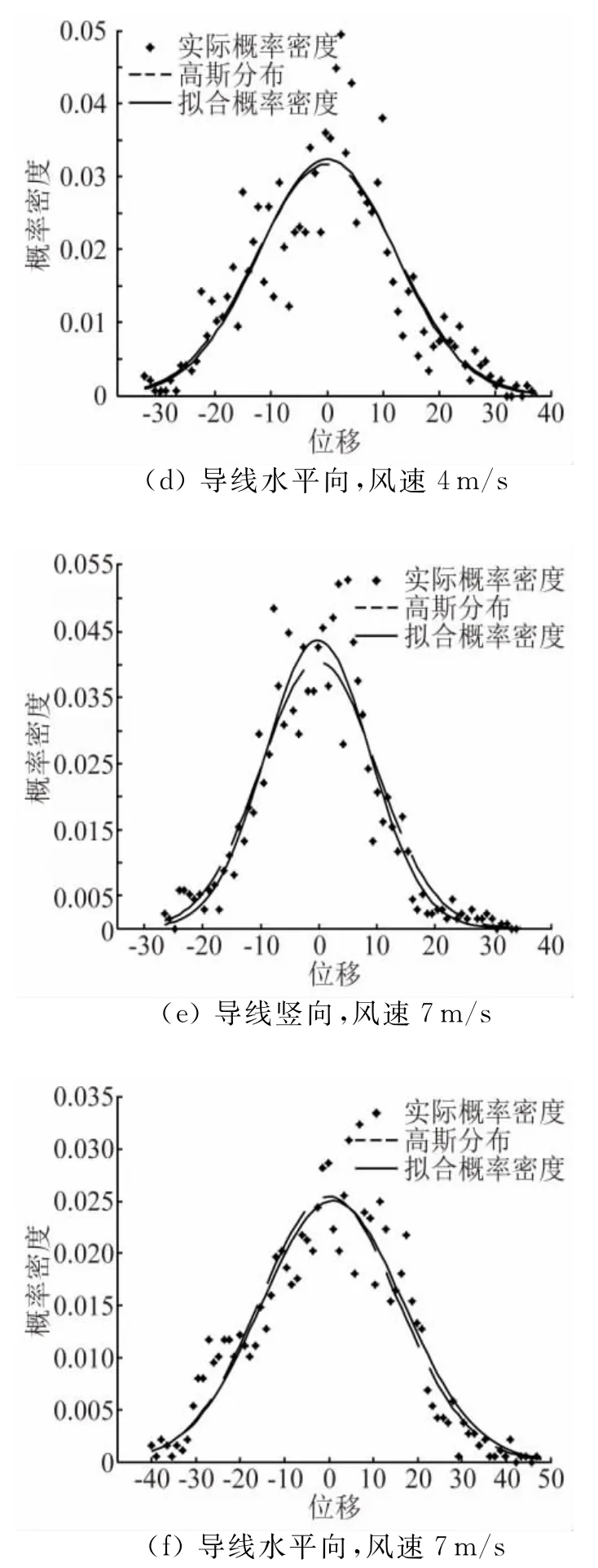
图14 导线跨中位移响应概率分布：Fig.14 PDF of displacements for intermediate measuring tap

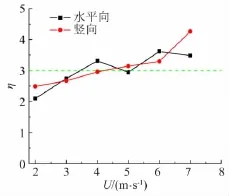
图15 位移响应峰因子Fig.15 Peak factors of displacement responses

4.5 导线风致运动特性分析

图16为导线跨中和1／4跨位置测点的运动轨迹。总体而言，导线的风致振动表现为一种混沌特性。对低风速而言，导线以水平向振动为主，竖向振动较小，导线跨中两个方向的振动较1／4跨具有更强的非线性耦合振动特性。对于高风速而言，导线跨中两个方向的耦合振动更类似如一个平面轨迹，此时发生较强的非线性耦合振动，而1／4跨的振动更为随机。

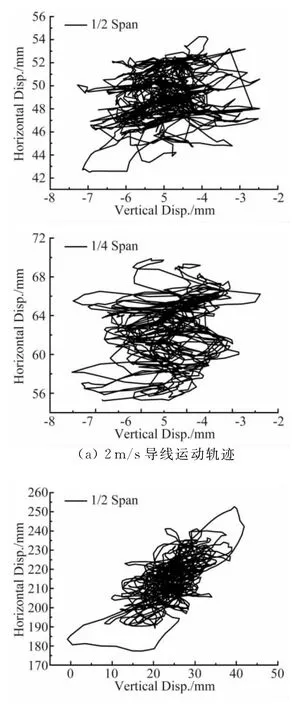
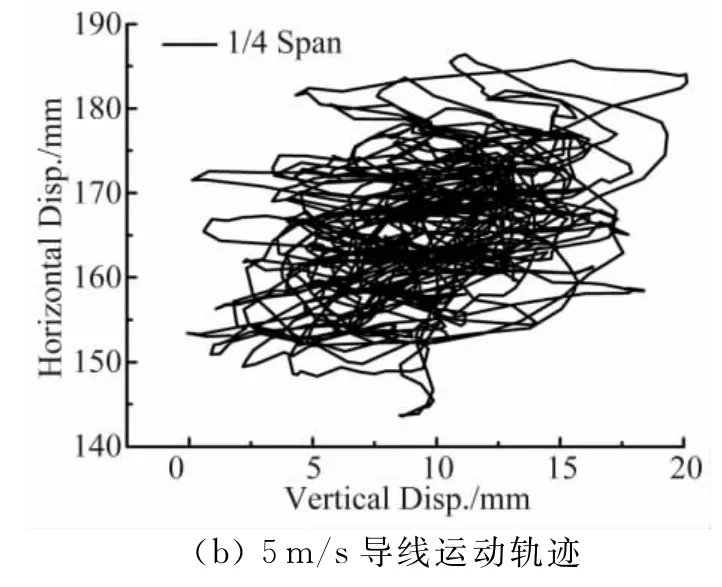
图16 位移响应轨迹图Fig.16 Trajectory diagrams of displacement responses

5 结 论

本文基于三维DICM的位移测试技术对导线沿跨多点位移进行了测试，并对位移进行了统计及频谱分析，得到如下主要结论：

1）三维DICM的位移测试技术对类似输电导线这种结构形式的风致三维耦合振动风洞试验测试技术的提升具有重要的意义；

2）导线的风致振动主要是一阶面外、一阶面内以及二阶面内对称振型起到控制作用，但对于非跨中位置位移响应的计算还应该考虑反对称振型的影响。

3）在风荷载作用下，随着风速的增加，输电线面内、外非线性耦合程度增强，其风致响应不再满足高斯分布，位移响应峰因子应作相应调整。

4）低风速时，导线以水平向振动为主；而高风速时，则发生两个方向的耦合振动，跨中位置的耦合振动较其他位置更强，其他位置的振动表现出更强的随机。

［1］Michael Fette，Juergen Voss，Liliana Oprea，et al.Modeling and simulation of high－voltage transmission lines with frequency dependent parameters［J］.Simulation Practice and Theory，1998，6：323－336.

［2］Pham Viet Hung，Hiroki Yamaguchi，Masanori Jsozaki，et al.Large amplitude vibrations of long－span transmission lines with bundled conductors in gusty wind［J］.Journal of Wind Engineering and Industrial Aerodynamics，2014，126：48－59.

［3］Loredo－Souza A M，Davenport A G.A novel approach for wind tunnel modeling of transmission lines［J］.Journal of Wind Engineering and Industrial Aerodynamics，2001，89：1017－1029.

［4］Wang Xin，Lou Wenjuan，Shen Guohui，et al.A wind tunnel study on aerodynamic characteristics of iced conductor［J］.Acta Aerodynamica Sinica，2011，29（5）：573－579.（in Chinese）王昕，楼文娟，沈国辉，等.覆冰导线气动力特性风洞试验研究［J］.空气动力学学报，2011，29（5）：573－579.

［5］Yan Bo，Liu Xiaohui，Hu Jing，et al.Wind－tunnel test for galloping of iced quad bundle conductors［J］.Acta Aerodynamica Sinica，2014，32（1）：109－115.（in Chinese）严波，刘小会，胡景，等.覆冰四分裂导线节段模型驰振风洞模拟试验［J］.空气动力学学报，2014，32（1）：109－115.

［6］Gurung C B，Yamaguchi H，Yukino T.Identification of large amplitude wind－induced vibration of ice－accreted transmission lines based on field observed data［J］.Engineering Structures，2002，24：179－188.

［7］Yao Lixin，Bao Qilian.Measurement of micro－displacement based on eddy current sensor and virtual instrument［J］.Measurement ＆Control Technology，2006，25（6）：13－15.（in Chinese）要利鑫，鲍其莲.基于电涡流位移传感器和虚拟仪器技术的微小位移测量［J］.测控技术，2006，25（6）：13－15.

［8］Chen Su，Chen Guoxin，Han Xiaojian，et al.Development for non－contact displacement test method and its application verification［J］.Journal of Basic Science And Engineering，2013，21（4）：725－734.（in Chinese）陈苏，陈国兴，韩晓健，等.非接触性动态位移测试方法的研发及应用验证［J］.应用基础与工程科学学报，2013，21（4）：725－734.

［9］Peters W H，Ranson W F.Digital imaging techniques in experimental stress analysis［J］.Optic Engineering，1982，21（3）：427－431.

［10］Chu T C，Ransom W F，Sutton M A，et al.Applications of digital image－correlation techniques to experimental mechanics［J］.Expriment Mechnics，1985，25（3）：232－245.

［11］Chen Haiyu，Xu Fuwei，Tao Li.Measurement of displacements in physical landslide model test based on noncontact optic measurement technique［J］.J of China Three Gorges Univ.（Natural Sciences），2005，27（6）：487－489，513.（in Chinese）陈海玉，徐福卫，陶莉.基于非接触式光学测量的滑坡模型位移测试［J］.三峡大学学报（自然科学版），2005，27（6）：487－489，513.

［12］Luo Xianqi，Chen Haiyu，Shen Hui，et al.Application of automatic mesh methods to landslide model test［J］.Rock and Soil Mechanics，2005，26（2）：231－234，238.（in Chinese）罗先启，陈海玉，沈辉，等.自动网格法在大型滑坡模型试验位移测试中的应用［J］.岩土力学，2005，26（2）：231－234，238.

［13］Chen Xujun，Lin Zhuming，Wu Guanghuai.Testing method and data analysis of moving－load－induced dynamic displacements of floating bridges［J］.Journal of Vibration，Measurement ＆Diagnosis，2006，26（2）：97－101.（in Chinese）陈徐均，林铸明，吴广怀.通载浮桥动态位移的测试方法与数据分析［J］.振动、测试与诊断，2006，26（2）：97－101.

［14］Ji Yunfeng.Computer vision approach for structure dynamic displacement measurement［J］.Jornal of Tongji University（Nature Science），2013，44（11）：1670－1674.（in Chinese）季云峰.结构动位移测试的计算机视觉方法实现［J］.同济大学学报（自然科学版），2013，44（11）：1670－1674.

［15］Irvine H M.Cable structure［M］.The MIT Press，1981.

［16］Wang Dahai，Li Jie.Nonlinear stochastic response of transmission tower－line system under strong wind［J］.Journal of Vibration and Shock，2009，29（6）：62－65.（in Chinese）汪大海，李杰.强风下高压输电塔线系统非线性随机动力响应［J］.振动与冲击，2009，29（6）：62－65.

Measurement and analysis of wind－induced dynamic displacements of transmission conductors based on 3－D DICM

Wang Shuliang，Liang Shuguo＊，Zou Lianghao，Yang Wei，Wu Peng

（China School of Civil Engineering，Wuhan University，Wuhan 430072，China）

Displacements along the transmission line were measured through the 3－D DICM（Digital image correlation method）.Statistics and spectra of the wind－induced displacements were analyzed，and the results illustrated that under the wind loads，horizontal vibration of the transmission line is dominated by the first symmetric out－of－plane mode coupled with certain participation of in－plane mode，and as the wind speed increases，the contribution of in－plane mode become significant；as to the vertical vibration of the transmission line，the dominated modes include the first symmetric out－of－plane mode，the first and second symmetric in－plane modes.Overall，three modes mentioned above can be chosen to analyze the wind－induced vibration of the transmission line，which are sufficient to reflect the main components of wind－induced vibration energy；with the increasing of wind speed，the PDFs of the wind－induced displacements are non－Gaussian any more，and peak factors should be adjusted accordingly.

3－D DICM；transmission line；wind tunnel test；aero－elastic model；displacement measurement

TU312＋.1

Adoi：10.7638／kqdlxxb－2014.0138

0258－1825（2016）04－0503－08

2014－12－16；

2015－02－25

国家自然科学基金（51078296）

王述良（1985－），男，硕士，博士研究生，研究方向：结构风工程.E－mail：diy1985＠126.com

梁枢果＊（1950－），男，硕士，教授，研究方向：结构风工程.E－mail：liangsg＠public.wh.hb.cn

王述良，梁枢果，邹良浩，等.基于三维数字图像相关法（DICM）的输电导线风致动态位移测试及分析［J］.空气动力学学报，2016，34（4）：503－510.

10.7638／kqdlxxb－2014.0138 Wang S L，Liang S G，Zou L H，et al.Measurement and analysis of windinduced dynamic displacements of transmission conductors based on 3－D DICM［J］.Acta Aerodynamica Sinica，2016，34（4）：503－510.