联合多代卫星测高数据建立江苏海域平均海面高模型研究

王敏

【摘 要】本文联合多代卫星测高资料，研究了基于支持向量机与共线平均算法的交叉点确定方法，利用多代卫星的交叉点平差，削弱了径向轨道误差；通过比较多种测高数据格网化算法精度，选择最优算法建立了江苏海域23年平均海面高模型。

【关键词】卫星测高；平均海面；支持向量机；格网化

0 引言

平均海面是物理海洋学与大地测量学的重要内容，它是由大地水准面与海面地形两部分构成，是研究大地水准面、分析地球内部动力学机制及地壳形变的重要基础数据。

为了计算高质量的平均海面模型，合理利用多源测高卫星数据成为其中的关键[1]。国内外一些学者已经先后研究出了多个平均海平面高模型。李建成等利用联合交叉点平差法计算了2.5′×2.5′的中国沿海平均海面高模型[1-2]；SLOOP利用卫星测高数据得到了消除海面时变影响的格网分辨率为2′×2′平均海面高模型MSS-CNES-CLS11[3]；CLS-CNES利用沿轨梯度值海面高替代法，选用二维傅立叶插值算法得到了格网分辨率为2′×2′的GFSC00 MSS平均海面高模型[4-5]；邓凯亮等学者联合GeosatGM、ERS21、T/P、T/P新轨道、ERS/2和GFO等卫星测高数据，确定了中国沿海2′×2′的平均海面高模型[1]。

本文联合Envisat数据、Envisat新轨道数据、ERS-1数据、ERS-2数据、T/P数据、T/P新轨道数据、Jason-1数据、Jason-1新轨道数据、Jason-2数据和GFO数据，确定了江苏海域格网分辨率为2.5′×2.5′的平均海面高模型。江苏海域研究区域为领海基线以内以及往深海区域延伸100海里的海域范围（31.44°N～36.07°N、119.18°E～123.93°E）。

1 研究数据

本文采用了Aviso发布的DT CorSSH卫星测高数据，数据列表如表1所示，所有数据基准均已统一到T/P卫星所在坐标框架上。同时数据已预先对干湿对流层、固体潮、电离层，风速等数据进行了改正[6]。

由表1可知，本文采用了共计23年（1992至2015年）的测高数据，其数据量及时间跨度较大，且数据均匀分布。

2 数据分析与处理

2.1 卫星弧段的拟合

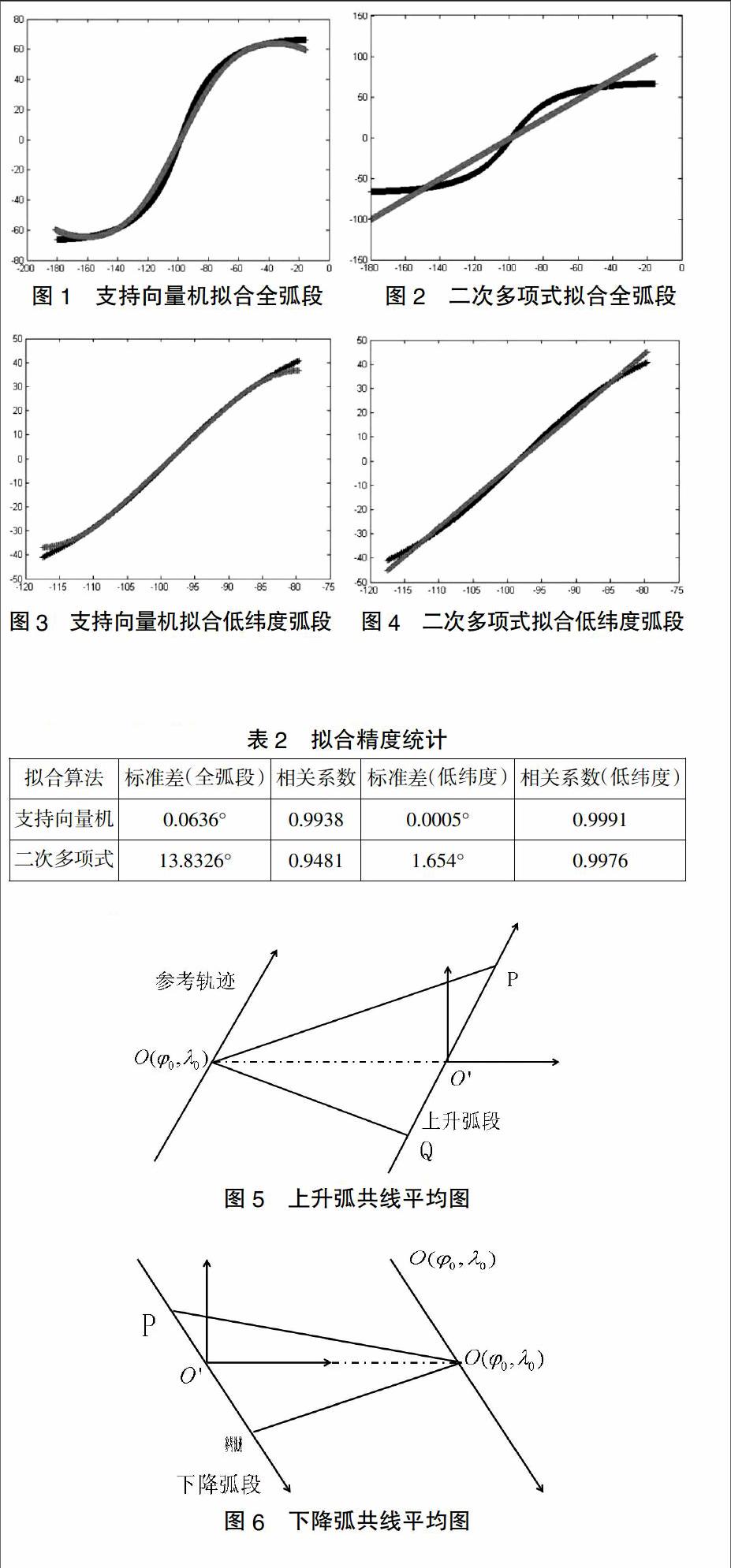
卫星测高数据存在径向轨道误差，主要反映在交叉点不符值上。交叉点不符值的确定对交叉点平差至关重要，其精度主要由交叉点位置决定[7]。弧段的曲线拟合方法直接影响交叉点概略位置的求解精度。本文利用支持向量机方法分别拟合一个全弧段及低纬度区域的弧段，并将其与二次多项式方法拟合结果进行了比较，拟合结果见图1、图2。两种方法拟合低纬度区域弧段结果见图3、图4。

由图1、图2、图3、图4可知，支持向量机方法在高纬度及低纬度区域拟合效果均优于二次多项式拟合。其二者拟合精度见表2。

表2 拟合精度统计

由表2可知，支持向量机拟合算法在小区域低纬度范围及全球范围内拟合精度较高，本文采用该算法进行弧段拟合。

2.2 共线平均

利用共线平均可减小线性变化和常量偏差造成的径向轨道误差[8]。该方法是通过选择合适的参考周期卫星轨迹来计算其它重复轨迹上相同纬度点的经度及海面高。共线平均示意图见图5、图6。

以图5、图6为例，O为参考点，O′为其它周期轨迹与O纬度相同的点。由于测高密度有限，因此该点一般不存在卫星测高数据。因此该点卫星测高数据，可利线性内插求取[8]。推导可得下降弧段与上升弧段的计算公式：

式中：λ为经度，ψ为纬度，H为海面高，D为共线轨迹弧段的斜率。

利用共线平均，可以削弱卫星轨道误差，同时可削弱如厄尔尼诺和拉尼娜现象等异常气候现象所引起的测高数据短波误差[1]，共线平均前后交叉点不符值精度如表3所示。

由表3可知，GFO、ERS-1、ERS-2、T/P、Jason-1、Jason-2、Envisat以及Evisat新轨道在共线平均后交叉点不符值精度均有所提高，表明经过共线平均短波误差得到较好的削弱。

2.3 联合交叉点平差

由于中长波误差的影响，共线平均后交叉点不符值精度（RMS）仍在0.94～6.2cm之间（见表3）。由于所有数据基准均统一在Jason-1、Jason-1新轨道以及Jason-2所在的坐标框架，且其精度最高。因此可认为，这三类测高数据受中长波误差影响最小。因此，采用这三个数据所在框架作为平均框架，并利用强制改正法[1]，削弱其余测高数据中长波误差，改正前后精度如表4所示。

由表4、表5可知，交叉点平差后，除固定框架的三类数据外，其余交叉点不符值精度均小于3.7cm。

2.4 格网化

本文选取了多种算法对江苏海域海面高数据进行格网化处理，交叉验证结果见表6。

由表6可得，克里金法格网化方法均方根误差、绝对值偏差平均值、STD均为最小。故本文选择克里金法进行格网化处理。

利用克里金法格网化后所得平均海面的等值线图（B、L、H）如图7所示。

由表6、图7可知，对江苏海域应用克里金格网化算法可以制作满足精度的平均海面数据。

3 精度评定

3.1 用MSS-CNES-CLS11海平面模型检验

MSS-CNES-CLS11使用了15年的TOPEX/POSEIDON、ERS-2、GFO、JASON-1、ENVISAT数据以及168天非重复周期的ERS-1数据，该模型的短波误差经过了很好的修正。由于MSS-CNES-CLS11默认分辨率为2′×2′，实验中对其进行了处理，转换为了2.5′×2.5′分辨率。为了进行外部精度检验，本文将计算的平均海面高模型与处理后的MSS-CNES-CLS11全球平均海平面高模型在江苏海域内进行了数值比较和验证。将由本文所建立的模型与MSS-CNES-CLS11在江苏海域内的格网值比较结果如表7，其所分析的数据为MSS-CNES-CLS11模型的值减本模型的值。

从表7可得，本文建立的江苏海域平均海面模型与MSS-CNES-CLS11模型差值的标准差是0.0814m，RMS为0.1484m。由此可得，本文所建立的江苏海域平均海面高模型正确、精度较高。

3.2 用Jason-1、Jason-1新轨道及Jason-2平均框架检验

由表3可知，Jason-1、Jason-2精度为各类卫星中最高。因此利用该平均框架来检验本模型的方法是可行的。本文利用260个周期的Jason-1数据、13个周期的Jason-1新轨道数据和160个周期的Jason-2数据按照共线平均法得到了平均框架。为了更为客观地反映本模型的精度，同样利用该框架对MSS-CNES-CLS11模型进行了比较。差值统计结果见表8。

由表8可以看出，本文所建立的平均海平面模型在江苏近海区域比MSS-CNES-CLS11的平均海平面模型的精度略优，预计精度优于10cm。

4 结论

本文研究了利用支持向量机方法拟合卫星测高弧段的理论，证明其能显著提高卫星弧段的拟合精度。利用共线平均，削弱测高数据短波误差，利用强制改正，削弱了中长波误差。选择（下转第46页）（上接第10页）克里金方法进行了数据格网化，最终建立了江苏海域平均海面高模型。将本模型与MSS-CNES-CLS11平均海平面高模型进行了比较，所得差值的均方根（RMS）为：0.1484m，标准差（STD）为：0.0814m。将本模型与Jason-1、Jason-2平均框架进行了比较，差值的均方根（RMS）为：0.0855m，标准差（STD）为：0.0841m。结果表明，本模型精度可靠，计算方法可行。

【参考文献】

[1]邓凯亮，暴景阳，许军，章传银.用强制改正法建立中国近海平均海平面高模型[J].武汉大学学报（信息科学版），2008，33（12）：1283-1287.

[2]姜卫平，李建成，王正涛.联合多种测高数据确定全球平均海面WHU2000[J].科学通报，2002，47（15）：1187-1191.

[3]MSS_CNES_CLS10 was produced by CLS Space Oceanography Division and distributed by Aviso，with support from Cnes（http：//www.aviso.oceanobs.com/）[OL].

[4]Hernandez F，Schaeffer P， Altimetric Mean Sea Surfaces and Gravity Anomaly maps Inter-Comparisons[R].AVISO Technical Report，AVI-NT-011-5242-CLS，Toulouse，France， 2000.

[5]赵倩，黄舒青，朱明磊.利用Jason-1卫星确定全球平均海面高[J].测绘信息与工程，2008，33（1）：4-6.

[6]AVISO/Altimetry.DTCorSSH and DT SLA Product Handbook[M].CLS-DOS-NT-08.341，2012.

[7]周晓光，苗洪利，王云海，等.卫星地面轨迹分段拟合确定交叉点的方法研究[J].测绘学报，2012，41（6）：811-815.

[8]陈俊勇，李建成，晁定波.用T/P测高数据确定中国海域及邻海的海面高及海面地形[J].武汉测绘科技大学学报，1995，20（4）：321-326.

[9]Hwang C， Hsu HY， Jang R J.Global Mean Sea Surface and Marine Gravity Anomaly from Multi-satellite Altimetry：Applications of Deflection-geoid and Inverse Vening Meinesz Formulae[J].Journal of Geodesy，2002，76（8）：407-418.

[责任编辑：王楠]