强冲击荷载作用下加无粘结预应力筋格栅坝动力响应分析

王秀丽，张嘉懿，陈 露

(1．兰州理工大学土木工程学院，甘肃兰州730050; 2．兰州理工大学西部土木工程防灾减灾教育部工程研究中心，甘肃兰州730050)

强冲击荷载作用下加无粘结预应力筋格栅坝动力响应分析

王秀丽1，2，张嘉懿1，2，陈 露1，2

(1．兰州理工大学土木工程学院，甘肃兰州730050; 2．兰州理工大学西部土木工程防灾减灾教育部工程研究中心，甘肃兰州730050)

泥石流拦挡坝主要以增加自身刚度来提高其拦挡能力，但对于巨石块的碰撞，坝体刚度越大，其受冲击力也越大，相应的坝体结构破坏也越大。创新性地将无粘结预应力筋设置在普通格栅坝中，利用ABAQUS软件对普通格栅坝和加无粘结预应力筋格栅坝在相同冲击条件下(以10m/s的冲击速度)坝体被撞后动能的变化、加速度响应值、位移值和Von-mises应力进行了有限元数值模拟计算与对比分析。结果表明:加无粘结预应力筋格栅坝比普通格栅坝能吸收更多的冲击能量，冲击方向的加速度响应值更小，具有更好的抗冲击性能。

格栅坝;强冲击荷载;无粘结预应力筋;ABAQUS;动力响应

泥石流是山区常见［1］的一种地质灾害，具有暴发突然、流速快、历时短和危害严重等特征，主要以冲撞和淤积两种方式对人类和环境造成危害。每年6～8月份的暴雨季节，泥石流灾害频繁发生，特别是我国西部地区，近年来泥石流灾害造成的人民生命及财产损失相当严重［1］。

泥石流防治手段主要采取在泥石流沟内设置拦挡坝用以拦截泥石流。拦挡坝坝型主要分为实体拦挡坝和格栅拦挡坝两种。格栅拦挡坝是采用旧铁轨、钢管、钢筋混凝土框架等结构形式来拦挡可能阻塞河道的巨石块［2］。

针对无粘结预应力筋的极限应力的计算，早在1949年 Baker［3］就提出折减系数的概念，随后Pannell［4］提出采用等效矩形区长度计算无粘结预应力筋的极限应力，陆洲导等［5］在火灾中考虑无粘结预应力混凝土框架在非线性全过程中的力学响应。

目前，拦挡坝坝体大部分通过提高自身刚度来增加其抵抗巨石冲击力的能力。然而，拦挡坝坝体其自身刚度越大受到的冲击力也越大，而坝体弹性变形能力有限，只能依靠塑性变形来消耗大部分的能量，这会对其结构造成一定的破坏，使其使用寿命减少。本文创新性地将无粘结预应力筋置入格栅坝中，无粘结预应力筋在与被施加预应力筋混凝土之间滑动，无应力，其消耗部分冲击能量，从而使混凝土塑性消耗的冲击能量减少，表明加无粘结预应力筋格栅坝坝体在巨石冲击下抗冲击性能更好。

1 计算模型及材料的选择

本文分别利用仿真模拟软件ABAQUS建立普通拦挡格栅坝(以下简称为普通格栅坝)和加无粘结预应力筋拦挡格栅坝(以下简称为加预应力筋格栅坝)的计算模型。

普通格栅坝基础采用底部固结，加预应力筋格栅坝采用底部铰接。普通格栅坝与加预应力筋坝体的尺寸均统一，坝高为9 m，依据日本学者对格栅坝间隔对堵塞率的影响分析［6］，设定格栅坝前后坝间隔为1．5 m，竖向间隔为1．5 m，格栅柱截面为1．5 m×1．5 m，格栅梁截面为1．5 m×1．5 m(见图1)，取被撞击的一榀框架进行格栅坝坝体抗冲击性能分析。

为避免材料差别对结果造成的误差，两个坝体均采用相同的材料，即强度为C40的混凝土，混凝土采用塑性损伤模型，其密度为2 500 kg/m3，弹性模量为32．5 GPa，泊松比为0．2;纵筋采用HRB400，箍筋采用HPB300，箍筋均间隔150 mm均匀布置，选择公称直径为9．5 mm、预应力大小为1 220 N/ mm2的无粘结预应力筋置于格栅柱中心，设置无粘结预应筋的初始应力为1 220 N/mm2［7］;钢球采用Q345钢材，其直径为1．5 m，泊松比为0．3，屈服强度为345 MPa，弹性模量为206 GPa，切线模量为2．06 GPa，密度为7 850 kg/m3。普通格栅坝和加预应力筋格栅坝钢筋骨架见图2。

图1 格栅坝坝体尺寸Fig．1 Dimension of the grille dam

图2 格栅坝钢筋骨架Fig．2 Reinforcement cage of the grille dam

2 有限元数值模型的建立

2．1 相互作用设置

本文结合实际情况，将混凝土各部件之间的相互作用使用tie(绑定)使之成为一个整体的混凝土框架;普通钢筋与箍筋使用tie(绑定)为一个整体，钢筋股价整体embed(内嵌)于混凝土框架内;无粘结预应力筋置于格栅柱的最中间，为保证无粘结预应力筋与混凝土部分之间产生滑移，无应力，采用coupling(耦合)接触;钢球与坝体相撞不考虑钢球变形，将其设定为钢体，钢球与格栅坝碰撞的面设置为硬接触。

2．2 网格划分

在ABAQUS/Explicit模拟冲击时各部件的单元库采用Exiplicit，几何阶次为线性单元。

普通格栅坝的混凝土部分的网格划分采用扫掠技术进阶算法(在合适的部分使用映射网格)，这样划分能产生均匀的网格，且计算较快、精度也较高，由于框架结构形式规整，其划分单元尺寸皆为300 mm×300 mm的小正方形，其网格划分见图3。

图3 混凝土框架网格划分Fig．3 Mesh generation of the concrete frame

普通钢筋粘结为一钢筋骨架整体，单元类型设定为truss(桁架)，T3D2单元。无粘结预应力筋置于格栅柱中心，其采用三折线模型［4］，单元类型设置为truss;同时为了保证无粘结预应力筋与混凝土之间只发生Y方向的位移，其与混凝土的约束采用coupling(耦合)约束［8］。钢筋骨架和无粘结预应力筋网格划分分别见图4和图5。

图4 钢筋骨架网格划分Fig．4 Mesh generation of the reinforcement cage

图5 无粘结预应力筋网格划分Fig．5 Mesh generation of the unbonded prestressed tendon

钢球的网格划分采用扫掠技术进阶算法，网格单元尺寸近似全局尺寸为170 mm，见图6。

图6 钢球网格划分Fig．6 Mesh generation of the steel ball

钢球初速度的确定是根据对舟曲三眼峪沟泥石流堆积区大块石的实地测量，得知沟口堆积扇区堆积的最大颗粒直径为7．5 m，从而计算得出泥石流中块石流速为10．95 m/s，灾害中泥石流流速为10．4 m/s，故本文设定钢球的初速度为10 m/s［9］。

3 模拟结果对比分析

3．1 动能分析

在耗能方面主要体现在拦挡物动能的改变［10］。普通格栅坝和加预应力筋格栅坝坝体的动能时程曲线见图7。

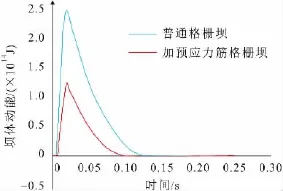
图7 格栅坝坝体动能时程曲线Fig．7 Time-history curves of kinetic energy of the grille dams

在撞击之前钢球的动能为6．749 2×1014J。由图7可见，在撞击后普通格栅坝的最大动能为2．313×1014J，加预应力筋格栅坝在撞击后最大动能为1．182×1014J，球体撞击后加预应力筋格栅坝的最大动能是普通格栅坝的1/1．957，因此很容易可以得出加预应力筋格栅坝在抵抗钢球冲击时能更好地吸收冲击能量。

3．2 加速度分析

冲击荷载作用下，结构的加速度响应尤其是最大加速度是一个重要参数，根据达朗贝尔原理，加速度会在结构中产生惯性力，结构在真实的外荷载、虚拟的惯性力共同作用下，处于动态平衡状态。在大多数工程材料中，应力波的传播速度很快，因而有限尺度的结构受到动荷载后将迅速达到平衡，这时应力波效应就消失了;但是结构自身还继续发生变形和整体运动，因而惯性效应还会持续相当长的时间，是不能忽略的［11］。

利用ABAQUS软件处理后，可模拟计算得出格栅坝坝体和钢球撞击后的最大加速度及其加速度时程曲线，见表1、图8和图9。由表1可见，钢球撞击加预应力筋格栅坝后其加速度减小很多，加预应力筋格栅坝中的钢球在X方向的加速度仅为普通格栅坝中的钢球的1/3．171，在Y方向的加速度仅为1/1．726。钢球撞击格栅坝坝体的速度和质量是一样的，但由于这两个格栅坝坝体刚度不同，在撞击过程中钢球受到的最大加速度相差很大，从而使钢球传给坝体的冲击力相差较大;很明显，加预应力筋格栅坝中的钢球传给坝体的冲击力比普通格栅坝减小很多。也就是说，相同冲击条件下普通格栅坝受到的冲击力更大，受到的破坏也就更大。此外，由表1可见，与钢球相反，加预应力筋格栅坝坝体在X、Y、Z方向的最大响应加速度比普通格栅坝坝体减小很多，最为明显的即为X方向，其为普通格栅坝最大加速度的1/11．93。

表1 钢球和格栅坝坝体在X、Y、Z方向的最大加速度(×103mm/s2)Table 1 Maximum acceleration of the steel balls and grille dams in theX，YandZdirection(×103mm/s2)

图8 钢球在X方向的加速度时程曲线Fig．8 Time-history curves of acceleration of the steel balls in theXdirection

由图8可见，加预应力筋格栅坝与普通格栅坝中的钢球的加速度在撞击过程中一直保持为正值，此后便减小为零且不变，这与实际较为符合，因为在撞击前后，钢球由向X轴正向运动变为了向X轴负向运动，最终保持匀速运动。

图9 格栅坝坝体在X方向的加速度时程曲线Fig．9 Time-history curves of acceleration of the grille dams in theXdirection

由图9可见，在撞击过程中，普通格栅坝坝体加速度值较大，坝体响应加速度在撞击结束后，其值基本保持在较大值且不停地上下波动、来回振荡，直到计算结束时坝体还没有稳定，说明在撞击结束后普通格栅坝坝体的惯性效应特别明显;而加预应力筋格栅坝在受撞击时最大的响应加速度小于普通格栅坝，且在撞击后加速度基本保持在零左右，其惯性效应优于普通格栅坝。

3．3 位移分析

利用ABAQUS软件处理后，可模拟计算得出格栅坝坝体在X方向的最大位移见表2。

表2 格栅坝坝体的最大位移Table 2 Maximum displacement of the grille dam

由表2可见，两个格栅坝坝体的变形均很小，加预应力筋格栅坝坝体在X方向的最大位移为44．07 mm，普通格栅坝坝体在X方向的最大位移为53．67 mm。

普通格栅坝和加预应力筋格栅坝最大位移节点在X方向的位移时程曲线见图10。

由图10可见，在0．07 s左右，普通格栅坝坝顶的位移到达峰值，而后其位移值减小至46．3 mm左右，加预应力筋格栅坝坝顶的位移值则一直减小，直至0．21 s后位移值在15．9 mm附近波动，其最大的位移仅为普通格栅坝的1/1．22。

图10 格栅坝坝体最大位移节点在X方向的位移时程曲线Fig．10 Time-history curves of displacement in theXdirection in the nodes with the maximum displacement of the grille dams

3．4 Von-mises应力对比

本文通过比较加普通格栅坝和预应力筋格栅坝的Von-mises应力来进一步评价这两种格栅坝抗冲击性能的好坏。利用ABAQUS软件处理后，可模拟计算得出普通格栅坝和加预应力筋格栅坝的Vonmises应力云图，见图11和图12。

图11 普通格栅坝的Von-mises应力云图Fig．11 Von-mises stress of the ordinary grille dam

图12 加预应力筋格栅坝的Von-mises应力云图Fig．12 Von-mises stress of the grille dam with unbonded prestressed tendon

由图11可见，普通格栅坝坝体在钢球撞击的瞬间，撞击位置处的应力立刻达到了混凝土的极限抗压承载力(图中深色部分)，说明撞击位置处的混凝土已经失效;随着冲击的进行，混凝土的失效面积逐步扩大，在冲击荷载达到峰值时，普通格栅坝坝体被撞击面积的混凝土全部失效，说明普通格栅坝被撞击的格栅柱已经破坏;此外，通过计算可知钢球撞击普通格栅坝坝体的整个时间很短，仅为0．036 s。

由图12可见，在钢球撞击加预应力筋格栅坝坝体的瞬间，即t=0．006 3 s时，撞击位置处的应力并未达到混凝土的极限抗压承载力，且撞击位置处的混凝土未失效;在冲击荷载达到峰值时，被撞击的格栅柱并未受到破坏。

对比图11和图12可见，相对于加预应力筋格栅坝，普通格栅坝的应力更为集中，更容易被破坏。通过计算可知钢球撞击加预应力筋格栅坝的时间仅为0．068 7 s，为普通格栅坝冲击时间的1．91倍。此外，由冲量定理I=F·t可知，在冲量大小相同时，当撞击时间t越长，冲击力F则越小，这一点正好印证了本文在前面所提出的结论:加预应力筋格栅坝坝体所受冲击力要小于普通格栅坝。

4 结 论

本文利用ABAQUS软件对普通格栅坝和加无粘结预应力筋格栅坝进行了动态有限元数值模拟计算与对比分析，得到如下结论:

(1)加预应力筋格栅坝与普通格栅坝相比，其坝体对于冲击能量能多吸收3倍;钢球撞击加预应力筋格栅坝后其加速度减小很多，加预应力筋格栅坝中的钢球在X方向的加速度仅为普通格栅坝中钢球的1/3．171，在Y方向的加速度仅为1/1．726，说明加预应力筋格栅坝具有更好的抗冲击性能。

(2)加预应力筋格栅坝在冲击作用下，坝体各处的变形比较均匀，材料得到充分利用，能够抵抗更大的冲击力，证明能够更好地缓冲泥石流的冲击。

(3)加预应力筋格栅坝在受到冲击后混凝土并未被撞坏，这是因为植入无粘结预应力筋的格栅坝为半刚性结构，在受到冲击后通过整体变形来分担部分冲击荷载，可发挥结构的整体性，且应力分布均匀，较普通格栅坝来说，减少了局部破坏，增加了坝体的使用寿命。

［1］张宇，王青，尹明．无铰拱形泥石流拦挡坝研究［J］．自然灾害学报，2006，15(2):20-24．

［2］王秀丽，黄兆升．冲击荷载下泥石流拦挡坝动力响应分析［J］．中国地质灾害与防治学报，2013，24(4):61-65．

［3］Baker A L L．A plastic theory of design for ordinary reinforce and prestressed concrete including moment redistribution in continuous members［J］．Magazine of Concrete Research，1949，1(2):57-66

［4］Pannell F N．Ultimate moment resistance of unbounded prestressed concrete beams［J］．Magazine of Concrete Research，1969，21(66): 43-54．

［5］陆洲导，李刚，许立新．无粘结预应力混凝土框架火灾下结构反应分析［J］．土木工程学报，2003，36(10):30-35．

［6］水山高久，小桥澄治，水野秀明．格子型リルの·-·流砂减少率に关する研究［J］．砂防学会志，1995，47(5):8-13．

［7］JGJ 92—2004 无粘结预应力混凝土结构技术规程［S］．

［8］郑炜鋆．无粘结预应力混凝土梁的ABAQUS有限元模拟［J］．福建建筑，2014，197(11):51-53．

［9］邓虎，陈宁生，胡桂胜，等．甘肃舟曲三眼峪沟泥石流动力学特征参数计算［J］．重庆交通大学学报(自然科学版)，2011，30(4): 833-838．

［10］楼铁炯．无粘结预应力梁的有限元建模与性能分析研究［D］．杭州:浙江大学，2005．

［11］郑国足，王秀丽，张守丽．带弹簧支撑的新型泥石流拦挡坝抗冲击性能研究［J］．防灾减灾工程学报，2014，34(5):551-558．

Dynamic Response of Grille Dam with Unbonded Prestressed Tendon under Strong Impact Load

WANG Xiuli1，2，ZHANG Jiayi1，2，CHEN Lu1，2
(1．School of Civil Engineering，Lanzhou University of Technology，Lanzhou730050，China; 2．Research Center of Western Civil Engineering Disaster Prevention＆Mitigation Attachedto Ministry of Education，Lanzhou University of Technology，Lanzhou730050，China)

The resistance ability of debris dam is mainly increased by improving stiffness of the dam．However，under the impact of stones，the bigger the dam’s stiffness is，the bigger impact force it bears，and the greater structural damage it gets．Based on this point，this paper innovatively sets unbonded prestressed tendon in the ordinary grille dam，and conducts the finite element numerical simulation and comparison analysis of the ordinary and improved grille dam by applying ABAQUS software．Under the same impact condition with impact velocity of 10 m/s，the paper compares the grille dams before and after the impact from the aspects including changes of kinetic energy，acceleration respon sevalues，dam displacement and Von-mises stress．The result shows that the grille dam with unbonded pestressed tendon absorbs more impact energy，and the acceleration response value is smaller．The grille dam with unbonded pestressed tendon exhibits better performance in impact resistance．

grille dam;strong impact load;unbonded prestressed tendon;ABAQUS;dynamic response

X93;P642．23

ADOI:10．13578/j．cnki．issn．1671-1556．2016．05．024

1671-1556(2016)05-0144-05

2015-11-03

2016-01-19

国家自然科学基金项目(51278236);国家科技支撑计划项目(2011BAK12B07)

王秀丽(1963—)，女，博士，教授，博士生导师，主要从事大跨度空间结构及泥石流防治技术方面的研究。E-mail:2024934784@qq．com