乘用车副车架计算模态分析边界当量方法研究
高继东 陈达亮 李洪亮 王海洋
(中国汽车技术研究中心,天津300300)
乘用车副车架计算模态分析边界当量方法研究
高继东陈达亮李洪亮王海洋
(中国汽车技术研究中心,天津300300)
【摘要】针对某车型刚性前副车架低频(0~200 Hz)有限元模态分析中车身边界当量处理方式的问题,对其中以橡胶衬套约束连接的柔性边界进行了合理简化,并对通过螺栓连接的车身边界提出了以车身连接点处动刚度导入作为边界约束的当量处理方法。计算模态与试验模态的对比分析结果表明,计算模态频率偏高问题得到纠正,模态频率计算误差控制在10%以内,验证了所提边界条件当量处理方法的合理性与可行性。
1 副车架安装状态分析
汽车副车架按其与车身的连接方式可分为弹性与刚性两种类型,前者通过橡胶衬套等弹性元件与车身连接,后者通过螺栓等与车身连接。一般认为,刚性副车架与车身的连接刚度远大于弹性副车架,甚至可近似为刚性连接。
现有某车型副车架为刚性连接,并且存在严重的低频(0~200 Hz)NVH问题。通过前期研究,已确定该问题与副车架有关,主要表现为车辆行驶于不平路面时,路面激励通过副车架传递至车身从而引起地板振动和车内噪声过大,因此需开展副车架结构动态特性有限元分析。
针对副车架的动态特性分析一般涉及自由模态、约束模态两个方面,并多以约束模态信息作为NVH问题分析与诊断的直接依据。采用有限元方法处理时,往往先实施自由模态分析并对分析结果加以验证,以此检视结构离散化处理及材质定义的合理性。在此基础上,引入边界条件进行约束模态分析。对于前述具体车型,其副车架的安装约束情况如图1所示,副车架与下摆臂内端、转向系统下端、横向稳定杆、发动机后侧悬置点处通过橡胶衬套弹性相连,而与车身则通过螺栓刚性连接在一起。孙凤蔚[1]等人将副车架与车身处理为刚性连接,该方法虽然简单、高效,但忽略了车身连接点局部刚度的影响,导致分析精度不高。为了克服以上缺点,提出将橡胶衬套、车身与副车架连接位置的动刚度值作为当量边界条件,在充分考虑车身连接点局部刚度的同时,避免了车身局部结构有限元建模与分析的繁琐,预期处理效果良好。
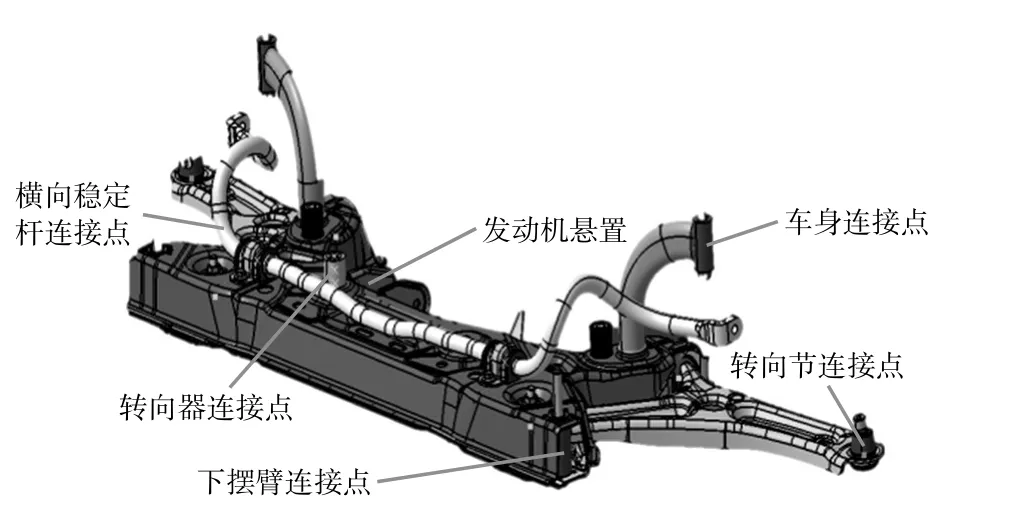
图1 副车架安装状态边界条件
2 副车架试验模态分析
为了验证该副车架结构有限元建模及分析的准确性,需进行副车架自由模态与约束模态测试。
2.1副车架自由模态测试
副车架自由模态测试通过橡胶绳悬挂的方式使其处于自由悬挂状态,并采用SIMO即单输入多输出的方式进行。测试结果如图2与表1所示,可知该副车架在自由状态下200 Hz以内仅有1阶模态,为170.6 Hz。
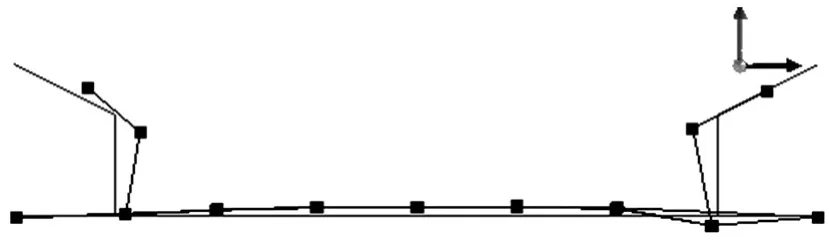
图2 副车架自由模态试验振型

表1 副车架自由模态结果对比
2.2副车架约束模态测试
约束模态测试在副车架装车条件下进行,测试同样采用SIMO方式进行,测试结果如图3所示。
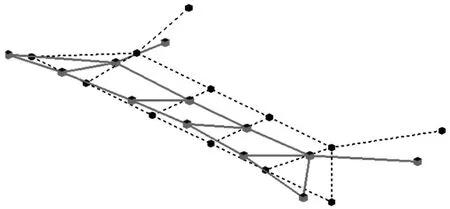
图3 副车架约束模态试验振型
3 副车架结构自由模态分析及验证
为了研究副车架边界条件的有限元当量方法,需进行副车架结构计算自由模态分析。在获取该副车架的三维模型之后,通过相关软件建立副车架有限元模型,其中网格单元大小为8 mm,网格类型为四边形或三角形壳单元,材质按实际属性赋予,焊缝以RBE2单元模拟,并开展模态分析,结果如表1与图4所示。

图4 副车架自由模态仿真分析振型
由表1、图3与图4可知,在200 Hz内副车架有限元自由模态计算与自由模态试验结果均仅有1阶模态,且振型相同,并且模态频率的误差为7.7 %,满足工程分析需要。因此,该有限元模型精度满足后续分析要求,可用于计算约束模态分析。
4 副车架弹性边界的定义与简化
橡胶衬套作为副车架的弹性边界条件,在计算模态分析中,由于其质量较轻,可忽略其质量对模态的影响[2]。橡胶材料动态特性受激振振幅和激振频率的影响[2],使橡胶衬套的动刚度随着激励频率和振幅的改变而变化,这种动刚度特性使得副车架与周围部件的边界条件随激励而变化,对副车架动态特性有较大影响,因此需考虑橡胶衬套的动刚度特性。考虑到计算复杂度的影响,在分析时选取试验模态峰值频率所对应的橡胶衬套刚度值作为橡胶衬套边界条件动刚度,并以弹性单元进行模拟[3~5],如图5所示(以横向稳定杆连接处衬套为例)。
4.1下摆臂
下摆臂内端与副车架之间通过橡胶衬套连接,外端通过球铰连接于转向节。在装配状态下,下摆臂相对副车架存在一定的浮动空间。由于下摆臂自由度过多,需要将其与副车架视为一个整体进行约束模态分析[6],因此在仿真计算时将下摆臂外端的球铰作为边界,下摆臂内端与副车架之间的橡胶衬套用赋予该衬套在175.9 Hz动刚度值的弹性单元进行模拟。
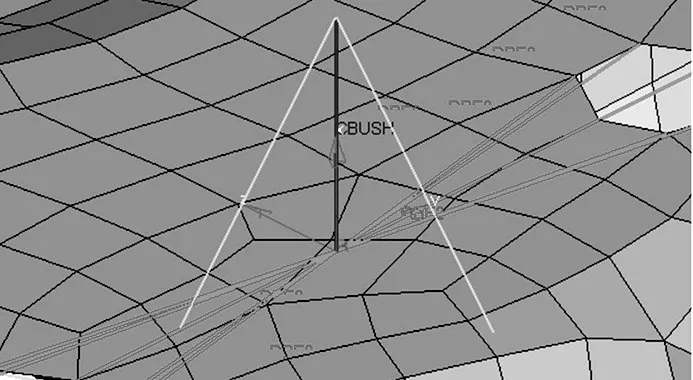
图5 弹性单元模拟橡胶衬套
4.2转向机壳体
转向机壳体通过3个衬套连接于副车架,且由于转向系统下端与车架固定连接,从而可将转向机壳体视为刚体,此处的3个衬套同样用赋予各衬套在175.9 Hz动刚度值的弹性单元进行模拟。
4.3横向稳定杆
横向稳定杆通过2个衬套连接于副车架。由于衬套的刚度远小于连接处横向稳定杆的刚度,因此将横向稳定杆视为刚体,并将衬套与横向稳定杆连接处作为边界,动刚度赋值方法同上。
4.4发动机
发动机后悬置通过橡胶衬套与副车架相连,其余悬置通过衬套与车架相连,因此发动机后悬置对副车架的约束较弱,其橡胶悬置对副车架产生的约束作用可忽略不计,不作为边界条件处理。
5 副车架车身边界的当量方法及验证
副车架通过螺栓与车身刚性连接在一起,但由于车身连接位置的刚度较低,不宜将车身边界视为刚体,并且基于橡胶衬套动刚度当量方法的思想,此处车身与副车架连接位置的边界条件可用车身连接位置在175.9 Hz处的动刚度值导入弹性单元来模拟。图6所示为副车架与车身边界条件当量方法模型示意。

图6 副车架与车身连接处边界条件有限元当量方法模型
为了验证副车架边界条件有限元当量方法的有效性,并与传统处理方法[1]进行对比,设计并实施了如下3种方法,
方法1:与副车架相连的橡胶衬套使用各衬套的静刚度值导入弹性单元进行模拟,其刚度值如表2所示,并将副车架与车身的螺栓连接视为固定副;
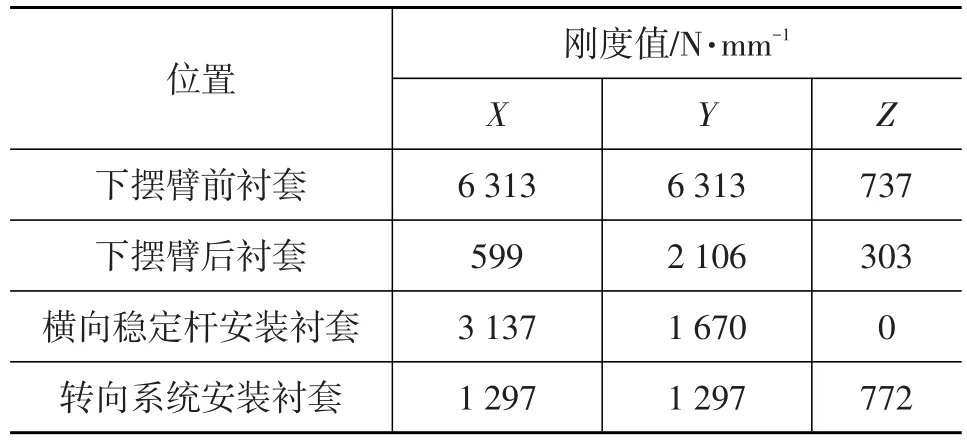
表2 副车架边界约束位置处各方向静刚度值
方法2:与副车架相连的橡胶衬套使用各衬套在175.9 Hz处的动刚度值导入弹性单元进行模拟,其刚度值如表3所示,副车架与车身的螺栓连接仍视为固定副;
方法3:副车架边界条件采用所提出的当量方法,即与副车架相连的橡胶衬套使用各衬套在175.9 Hz处的动刚度值导入弹性单元进行模拟,副车架与车身的螺栓连接使用车身连接位置在175.9 Hz处的动刚度值导入弹性单元进行模拟,所使用的各边界约束当量动刚度值如表3所示。
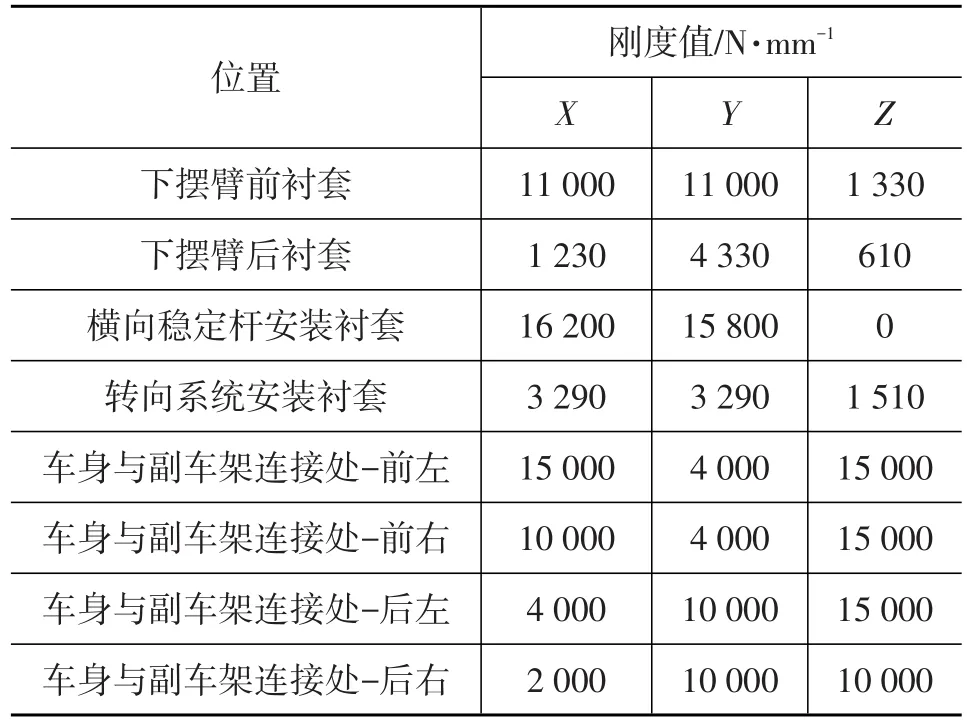
表3 副车架边界约束位置各方向175.9 Hz处动刚度值
上述方法1~方法3的仿真结果如图7~图9所示,副车架约束模态结果对比如表4所列。由此可知,方法1的仿真结果虽然振型与试验吻合,但是1阶模态频率与试验值误差太大,超过100 %,该方法仿真结果不可信;方法2将橡胶衬套在175.9 Hz处的动刚度值带入仿真计算,仿真与试验振型吻合,并且缩小了1阶模态频率计算结果与试验结果的误差(22.9 %),但该方法仿真模态频率仍偏高;方法3的仿真结果不仅振型与试验相同,且1阶模态频率计算值与试验值非常接近,误差只有2.3 %,验证了该方法的准确性与有效性。因此,该当量方法能够揭示副车架在实车状态下的动态特性,可用于刚性副车架约束模态的有限元建模与分析。

图7 副车架自由模态振型仿真(方法1)

图8 副车架自由模态振型仿真(方法2)

图9 副车架自由模态振型仿真(方法3)
6 结束语
建立了副车架结构有限元模型,并通过与自由模态测试结果对比,验证了该有限元模型的有效性。
提出了以橡胶衬套在试验模态频率点动刚度值代替静刚度值作为弹性边界条件的当量方法,以及以车身与副车架连接位置在试验模态频率点动刚度值代替固定约束作为刚性边界条件的当量方法。通过对比与分析,验证了该当量方法的有效性与正确性。
参考文献
1孙风蔚,徐昊,陈杰龙,等.某车前副车架模态分析与改进.汽车工程学报, 2012.
2余振龙,具龙锡.轿车悬架橡胶衬套结构特点分析.汽车技术, 2009.
3宋纪侠,雷明星,董慧利,等.某轻型商用车整车模态有限元分析研究.河南工程学院学报(自然科学版), 2014.
4段巧玉,姚寿广,许江涛.基于Hyper Mesh的副车架有限元分析.科学技术与工程, 2008.
5张焜煌,钱彦岭,徐慧峰,等.基于Nastran的粘性和粘弹性人工边界的模拟与验证.兵工自动化, 2009.
6史建鹏,管欣.悬架下摆臂的疲劳寿命分析.汽车工程, 2013.
7石少亮,吴伟蔚,黄虎,等.车用橡胶衬套的非线性有限元分析.机械设计与制造, 2011.
(责任编辑帘青)
修改稿收到日期为2015年12月1日。
Investigation on Equivalent Method of Front Subframe Boundary Conditions of Passenger Car for Computational Modal Analysis
Gao Jidong, Chen Daliang, Li Hongliang, Wang Haiyang
(China Automotive Technology and Research Center, Tianjin 300300)
【Abstract】To find the equivalent processing method about the body boundary conditions of the finite element modal analysis for the rigid front subframe low frequency (0~200 Hz) of a vehicle model, the flexible boundary of rubber bushes constraint joining are simplified and the bolted connection between the vehicle body and the front subframe is defined as the local dynamic stiffness. The method is applied to calculate the constrained modal analysis of a front subframe. The results show that the numerical error of the computational modal frequencies compared with the experimental ones is under 10% and the equivalent method is validated reasonably and feasibly.
Key words:Subframe,Boundary conditions,Dynamic stiffness,Modal analysis
中图分类号:U463.32
文献标识码:A
文章编号:1000-3703(2016)02-0042-03
主题词:乘用车副车架边界条件动刚度模态分析

