基于Benford法则的保险欺诈识别研究
张伟科
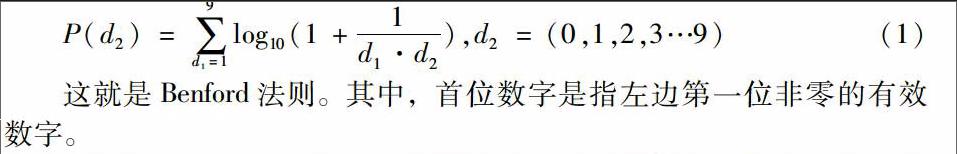

摘要:随着保险业的发展,保险欺诈呈现蔓延态势,如影随形,医疗保险欺诈已经成为大数据时代研究的方向和核心。本文利用在实践中广泛应用的数据质量检验方法Benford法则以及统计检验方法,以某保险公司医疗险理赔数据为样本,检验Benford法则在识别医疗保险欺诈的有效性和可行性,并采用统计检验的实证研究方法,从而找出可能存在保险欺诈样本的方法。
关键词:Benford法则;医疗保险;保险欺诈;统计检验
一、文献综述
Benford法则由美国数学家、天文学家Simon Neweomb在1881年首次发现。到了1938年,美国GE的物理学家Frank Benford注意到同样的现象,并且通过大量的数据对该观点进行了证实。Benford法则作为一种简单易行的数据检测方法,已经在经济审计等领域得到了广泛的应用。Carlaw(1988)通过Benford法则对新西兰证券交易所所有上市公司的收益数据进行了统计分析,结果显示收益数据存在着认为操纵迹象。Thomas(1989)运用Benford法则分析了美国上市公司净利润的前两位数字,研究显示盈利和亏损公司对净利润存在着人为操纵行为。Nigrini(1977)将Benford法则应用到了税务、会计等领域。Pericchi.L(2011)将Benford法则应用到了美国总统选举是否公平的检测。综上所述,Benford法则在经济等领域中得到了大量的应用。
二、Benford法则的基本原理
经过研究,Frank Benford得出这样的一个结论:对于大量自然统计数据,每个位置上的数字分布存在着一定的规律,呈单调下降趋势。其首位数字是数字d2的概率分布为:
P(d2)=∑9d1=1log10(1+1d1·d2),d2=(0,1,2,3…9)(1)
这就是Benford法则。其中,首位数字是指左边第一位非零的有效数字。
根据Benford法则,没有人为操纵的高质量数据各个位置上数字的分布应该遵循上述规律,并且样本越大,这种概率分布越应该符合Benford法则。如果存在欺诈或者弄虚造假的行为,这种概率分布规律可能被打破。可以用x2拟合优度检验和Pearson相关系数等方法来检验各个位置上数字的概率分布是否符合Benford法则。
三、实证结果与分析
本研究的数据全部来源于某人寿保险公司理赔数据,包括2013年1月至2014年10月所有医疗险理赔数据,其中删除了拒赔和赔付金额为0的数据样本。
本文将从两个方面对保险理赔数据的准确性进行统计分析。首先对保险理赔数据首位数字1至9这九个自然数和第二位数字0至9这十个自然数分别利用Benford法则进行可靠性分析。然后运用非参数统计中的x2拟合优度检验来估计每个数字出现的次数和Benford法则期望次数之间分布的整体拟合程度,利用z值来检验具体每个数字的出现频率的差异程度,从而验证保险理赔数据的首位和第二位数字的分布规律与Benford法则下的期望规律是否一致。x2检验的公式如下:
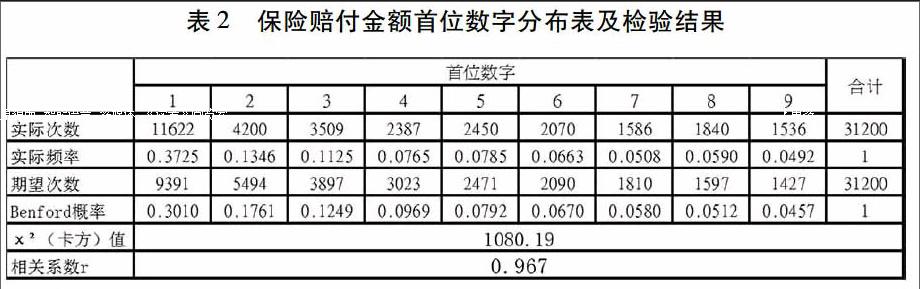
首先我们通过表2来观察保险理赔数据首位数字出现的次数和频率与Benford法则是否一致。
从表2可以看出,保险理赔金额首位数字的实际频率总体上呈递减趋势,但是首位数字5的分布频率稍大于数字4的实际频率,首位数字8的实际频率稍大于数字7的实际频率,首位数字1的实际频率明显大于Benford法则的期望频率,首位数字2的实际频率明显小于Benford法则的期望频率,其他数字的频率分布与Benford法则的期望频率相差较小。以上差异是否在我们可以接受的范围内,本文利用统计量进行拟合优度x2检验和Pearson相关系数检验,结果如表2所示。
从表2可以看出,在0.05显著性水平下,8个自由度的x2临界值为15.507,而保险赔付金额首位数字的x2检验值为1080.19,远大于临界值15.507,所以我们拒绝H0假设,接受H1假设,即赔付金额的首位数字出现次数与Benford法则的期望次数有显著差异,换句话说,赔付金额存在着人为操作因素,可能存在着保险欺诈。结合相关系数r=0.967,可以看出保险赔付金额首位数字与benford法则存在着显著的相关性,但是Pearson相关系数r≤0.97,可以认为该保险理赔数据存在着欺诈。
四、结论
本文从一个全新的视角,运用Benford法则对某保险公司2013年1月至2014年10月医疗险理赔数据是否存在欺诈进行了分析研究。从x2检验结果和Pearson相关系数值来看:首位数字分布的x2值为1080.19,远大于0.05显著性水平下、自由度为8的x2分布临界值15.507,相关系数r=0.967<0.97,因此我们可以认为该保险赔付数据首位数字是不准确的,存在着欺诈;综合上述分析,笔者认为该保险公司医疗险赔付数据不符合Benford法则,存在着保险欺诈。
参考文献:
[1]许涤龙;基于Benford法则的M2统计数据准确性研究[J],统计与信息论坛,2010(8)
[2]曾五一,薛梅林;GDP国家数据与地区数据的可衔接性研究[J],厦门大学学报(哲学社会科学版),2014(02)
[3]刘云霞等;关于综合运用Benford法则和面板模型检测统计数据质量的研究[J],统计研究,2012(11)

