不确定条件下的区间两阶段模糊可信性约束规划配水模型研究

张成龙，郭 萍，赵建明

(中国农业大学中国农业水问题研究中心 水利与土木工程学院，北京 100083)

黑河中游干旱少雨，水资源有限，短缺形势严峻，加之，2000年开始实施的黑河干流跨省区分水方案，限制了中游地表水资源可利用量[1]。同时，黑河中游农业用水占到总用水量的80%以上，水资源总量的80%以上来自黑河。农业用水的增加，导致整个流域农业用水和生态用水、中游用水和下游用水的矛盾日益尖锐[2]。因此良好的水资源管理规划有助于区域农业生产和经济发展。由于中游地区有限的地表水资源，决策者可通过优化配水方案得到最大的经济效益，即把水资源合理地分配到不同区域内的不同作物。同时，在农业灌溉系统中，存在许多不确定性问题。例如：灌溉水可利用量，灌溉水量目标，和灌溉定额，这些参数很难得到精确的量化的数据。因此，近年来，许多不确定性水资源优化配置方法被用于水资源管理系统中[3-8]。

在灌溉水资源优化配置系统中，水量分配的越多，农民将会获得更大的经济效益，但是在来水水平很低时，农民会面临很大的缺水损失；相应的，降低灌溉目标也就降低了缺水损失，但是效益也会随之减少。因此，如何通过建立模型来平衡灌区农业水资源供需矛盾，是灌溉水资源优化配置需要解决的问题。两阶段规划 (Two-stage Stochastic Programming, TSP) 是解决这类问题的有效方法，尤其是在不确定性条件下的水资源系统中。在TSP模型中，如果随机事件不确定，需要先确定第一阶段，当随机事件确定之后，再进行第二阶段的修正来减少系统惩罚损失[5-7]。在实际中，管理者通常要考虑系统中的不确定性带来的风险违规问题。TSP模型能够有效处理不确定性，但不能处理带有风险违规的不确定性问题。机会约束规划(Chance-constrained Programming, CCP) 和模糊可信性约束模型(Fuzzy Credibility Constrained Programming, FCCP) 都能有效解决此类问题。这类方法不要求所有的约束必须严格满足，相反，只需在给定的违规概率/置信水平下部分满足。但是，CCP在实际应用中，不确定性信息常常不能满足概率分布函数的要求，而模糊分布信息则比较容易获得[9]。并且，当系统中存在模糊变量时，只有基于可信性测度而建立的模糊可信性约束模型能解决此类问题[10-12]。因此，可把FCCP模型结合到TSP模型中，建立TFCP (Two-stage Stochastic Fuzzy Credibility Constrained Programming) 模型用以解决带有违背概率的模糊风险问题。TFCP模型可解决约束右侧的模糊参数问题，但不能处理约束左端和效益系数的不确定性问题，因此可引入IPP (Interval Parameter Programming)模型，有效补充TFCP模型的应用范围，最终得到ITFCP模型。通过Lingo软件进行模型求解，得到不同情景的优化决策方案。不同置信水平下的结果可帮助管理者衡量系统的不确定性，去制定合适的政策。

1 模型的建立

1.1 两阶段随机规划(TSP模型)

TSP模型可有效平衡不确定性条件下的灌溉农业水资源。通常，模型如下：

maxf=cx-E[Q(y,δ)]

(1)

式中：δ是第二阶段的决策变量，是随机变量，概率分布很难确定。

因此，可将不同来水水平情况下的缺水量按照离散变量处理，并对应不同来水水平出现的概率为ph：

(2)

(3)

模型线性形式如下：

(4)

约束条件：

Ax≤b

(5)

T(εh)x+W(εh)=g(εh) ∀h=1,2,……,H

(6)

x≥0

(7)

y(εh)≥0

(8)

通常，系统的决策变量被表示为带上下界的区间参数。所以将IPP结合到TSP模型中，即得区间两阶段随机规划(ITSP)模型：

(9)

约束条件：

A±x±≤b±

(10)

T(ε±h)x+W(ε±h)=g(ε±h) ∀h=1,2,…,H

(11)

x±≥0

(12)

y(ε±h)≥0

(13)

ITSP模型能够有效处理随机不确定性，但不能处理带有风险违规的不确定性问题。特别是当系统中存在模糊变量时，只有基于可信性测度而建立的模糊可信性约束模型能解决此类问题。

1.2 模糊可信性约束规划模型

模糊可信性约束规划模型为[13]：

(14)

约束条件：

(15)

xj≥0j=1,2,…,n

(16)

假设ξ为三角模糊变量(r1,r2,r3)：μ为隶属函数，x为实数；则x≤ξ的可信性可表示为：

(17)

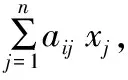
(18)

约束条件：

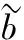
(19)

xj≥0j=1,2,…,m

(20)

将此式带入模型求得最优解。由上述模型可知，模糊可信性约束规划模型转化为一个线性规划模型，可以按照线性规划模型的解法求解。

1.3 区间两阶段模糊可信性约束规划

综合上述模型，本文建立了区间两阶段模糊可信性约束规划(ITSFCP)模型用于水资源优化配置，目标函数是在满足各项约束条件的前提下，达到利益最大化。约束条件包括：3个地区作物总的需水量和供水量，最小需水量约束，土地面积约束，非负约束等。模型如下：

目标函数。

约束条件。

(1)可利用水量约束：

(23)

∀h,l=1,2,…,m

(2)种植面积约束：

DT±ijh≤AT±ij,∀i,j,h

(24)

AT±ij-DT±ijh≥Aijmin,∀i,j,h

(25)

(3)非负约束。

DT±ijh≥0,∀i,j,h

(26)

2 模型求解

在上述模型中，AT±ij是区间形式的，因此线性规划的方法通常不能直接应用。因此引入决策变量zij，zij∈[0,1]，令AT±ij=AT-ij+zijΔATij，其中ΔATij=AT+ij-AT-ij，zij是确定值，因此AT±ij可用线性规划方法求解。当zij=0时，AT±ij取最小值，结果为模型下限；当zij=1时，AT±ij取最大值，结果为模型上限。通过求解得到优化决策变量zijopi，则AT±ijopt=AT-ij+zijoptΔATij。同时，根据区间交互算法，因为目标函数是经济效益最大，需要先进行符合f+的模型计算，扩大决策空间。

2.1 上限子模型

目标函数：

(27)

约束条件：

(1)可利用水量约束：

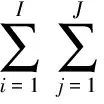
(1-2λi)(Qshηs+Qghηg-Qshηs-Qghηg)

(28)

(2)种植面积约束：

DT-ijh≤AT-ij+zijΔATij,∀i,j,h

(29)

AT-ij+zijΔATij-DT-ijh≥Aijmin,∀i,j,h

(30)

(3)非负约束：

DT-ijh≥0,∀i,j,h

(31)

式中：DT-ijh和zij是上限子模型的决策变量；f+opt，DT-ijh和zijopt是优化解，优化灌溉目标为AT±ijopt=AT-ij+zijoptΔATij。

2.2 下限子模型

目标函数：

(32)

约束条件：

(1)可利用水量约束：

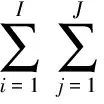
(1-2λi)(Qshηs+Qghηg-Qshηs-Qghηg)

(33)

(2)种植面积约束：

DT-ijh≤DT+ijh≤AT-ij+zijoptΔATij,∀i,j,h

(34)

AT-ij+zijoptΔATij-DT+ijh≥Aijmin,∀i,j,h

(35)

(3)非负约束：

DT+ijh≥0,∀i,j,h

(36)

式中：DT+ijh是决策变量；f-opt，DT+ijh是优化解。

因此，模型的优化解如下：

f±opt=[f-opt,f+opt]

(37)

DT±ijhopt=[DT-ijh,DT+ijh]

(38)

AT±ijopt=AT-ij+zijoptΔATij

(39)

3 实例研究

3.1 基本资料

以黑河中游甘州，临泽，高台的3种作物：夏收作物，秋收作物，经济作物为研究对象，进行优化配水。表1是不同地区不同作物的灌溉目标，灌溉定额和相关的经济参数。如果水量足够的话，可以获得一定的经济效益，如果水量短缺，就会缩减当前的规划或者从其他途径获取更多的水量，从而会有相应的惩罚，导致经济效益的损失。本模型中地表水和地下水的可利用水量是随机的，同时带有模糊属性，可看作为模糊随机变量，将其变成离散变量及其相应的概率。不同水平年地表水地下水可利用水量是三角模糊数(r1,r2,r3)，不同来水水平可能出现低流量、中流量、高流量3种情况，3种流量出现的概率分别为0.2、0.6、0.2。表2是地表水和地下水不同来水水平的可利用水量及其概率。地表水和地下水的灌溉水利用系数分别为η1=0.5，η2=0.65。一般来说，有意义的可信性置信水平应该大于0.5，见表3[11]。分别取可信性置信水平为1，0.9，0.875，0.85，0.8进行对比。

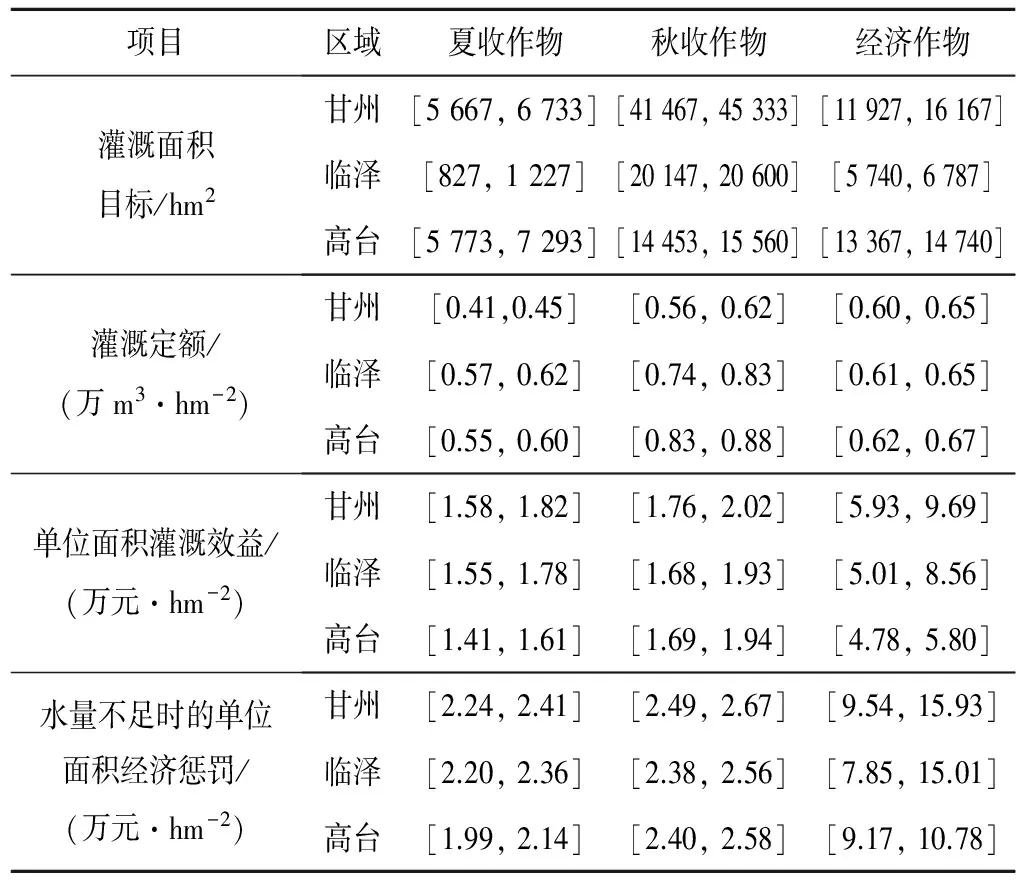
表1 灌溉面积目标及相关经济参数Tab.1 Irrigation targets and relevant model's economic parameters

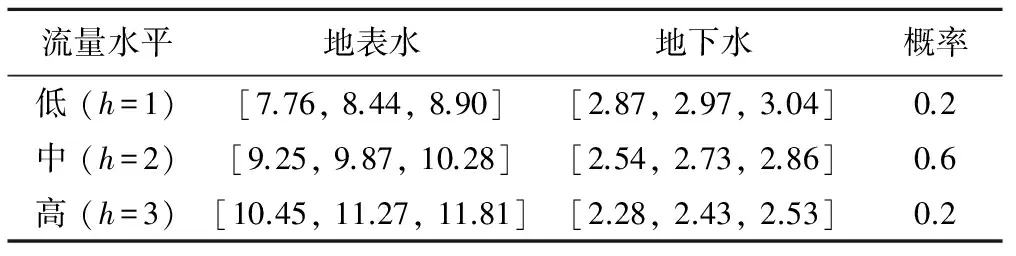
表2 可利用水量及概率分布Tab.2 Available water and corresponding probability distribution

3.2 结果分析

表4是不同可信性置信水平λl下的优化灌溉目标结果。对比不同地区的3种作物的灌溉面积，可知不同地区的不同作物之间存在用水的竞争。当可信性置信水平从λ=1到λ=0.8时，甘州区的夏收作物的优化灌溉面积不断增大，从5 667～6 733 hm2，分别是预先给定的灌溉目标的下限(zij=0)和上限(zij=1)。结果表明，随着可信性置信水平的降低，分配到该地区对应于夏收作物的水量不断增加，同时会面临伴随的缺水违规风险。如果管理者希望有更多的灌溉面积，则要面临较高的系统风险，导致可靠性降低。同时，3个地区的经济作物和秋收作物的结果分别是上限(zij=1)和下限(zij=0)，表明了管理者对经济作物的灌溉面积持积极态度，对秋收作物的灌溉面积持保守态度。因为两种作物的单位经济效益的不同，经济作物的收益较高，水量会优先满足；秋收作物的种植面积较大，应当适当压缩。

表3 可信度水平分类表Tab.3 The classification of credibility levels

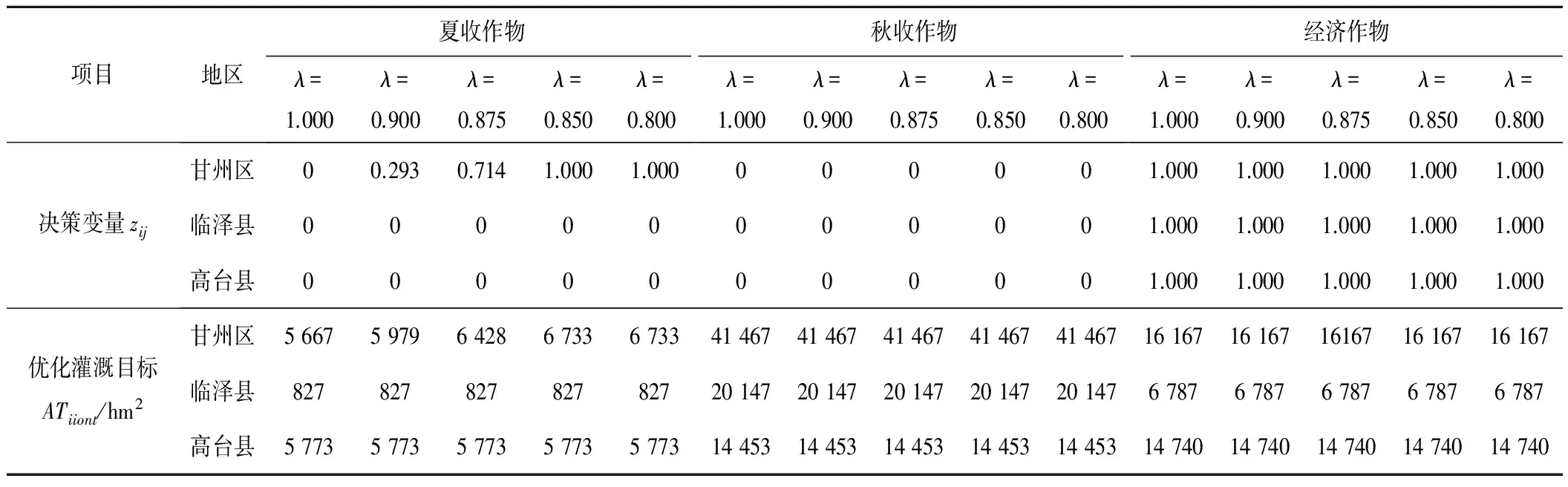
表4 不同可信性置信水平 下的优化灌溉目标结果 Tab.4 Optimal irrigation targets under different credibility levels

考虑不同可信性置信水平λl下的缺水作物灌溉面积，不同来水水平时缺水量是不同的，因此低流量水平时缺水灌溉的面积较大，高流量水平时缺水灌溉面积较小。以可信性置信水平λl=0.9为例，低水平(h=1)时，甘州区的秋收作物由于缺水而不能灌溉的面积是[16 465, 22 085] hm2；中水平是[3 338, 10 078] hm2；高水平时没有缺水。因此，如图1所示，实际的灌溉面积随着不同来水水平而增加。

图1 置信水平为λl=0.9时实际灌溉面积Fig.1 Actual irrigated crop area under λl=0.9 level

根据模型可得到系统的经济收益，给出了区间上下限f-opt和f+opt的结果。由于不确定性的可利用水量，结果应在此区间波动。上限的结果是在可利用水量更多的情景下得到，水资源短缺较少，但同时违规缺水风险较大；下限的结果则相反。因此，管理者需要平衡经济收益和缺水风险。由于λ=1代表系统需求条件下的最高可信度水平，因此λ的不同取值所得到的系统收益代表了不确定性约束条件下满足系统目标及约束水平的可信度水平。不同可信性置信水平对应的经济收益分别是λ=1时[23.36, 34.79]亿元，λ=0.9时，[23.65, 35.06]亿元，λ=0.875时[23.71, 35.13]亿元，λ=0.85时[23.78, 35.19] 亿元，λ=0.8时[23.92,35.32]亿元。由图2和图3分别是不同置信水平条件下的经济收益和缺水经济损失对比。可看出，随着可信性置信水平的降低，经济效益呈现增加的趋势，缺水经济损失逐渐变小。表明随着系统的风险违规程度的增加，系统可靠性程度降低，从而导致可利用水量的约束放松，相应的可利用水量增加，决策空间扩大，因而带来更多的经济收益。因此，系统收益和约束满足程度之间的权衡可为管理者提供不同的决策方案。

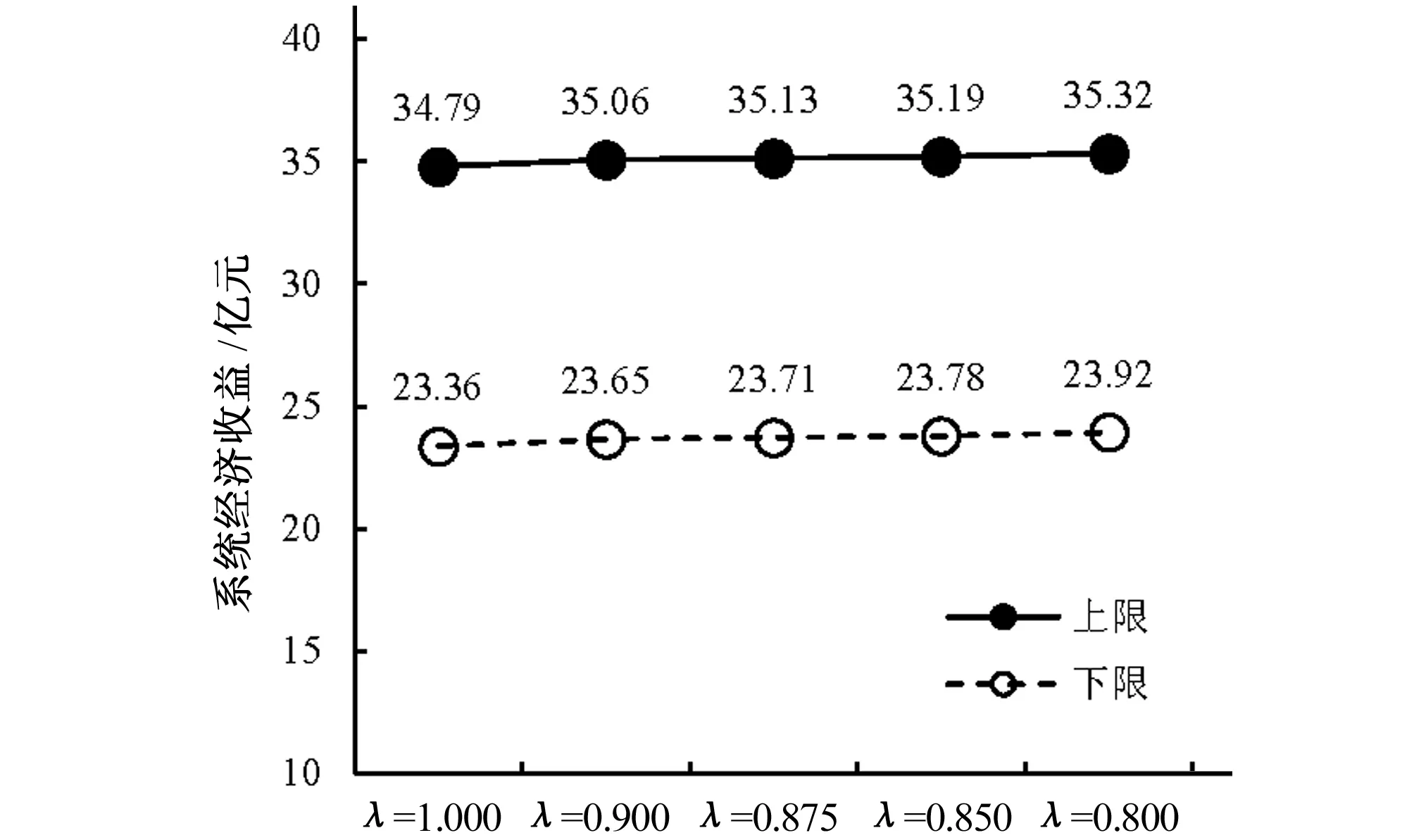
图2 不同可信性置信水平下的经济收益Fig.2 System benefits under different credibility levels

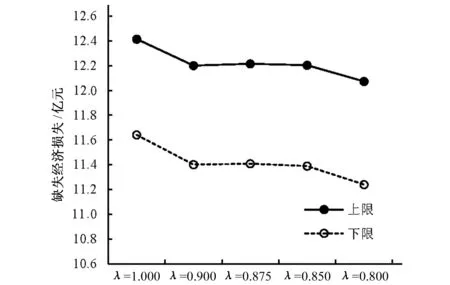
图3 不同可信性置信水平下的缺水经济损失Fig.3 System economic losses under different credibility levels

4 结 语

本文建立了不确定条件下的区间两阶段模糊可信性约束规划模型，用于黑河中游灌溉农业水资源优化配置。该方法扩展了区间两阶段随机规划和约束违规的情景，考虑用模糊可信性约束规划解决带有违背概率的模糊风险问题。模型可处理离散区间、概率密度函数和模糊变量的不确定性，能更实际的反映灌区水资源管理的不确定性。不同置信水平下得到的结果可帮助管理者更深入的了解系统的不确定性，并可按照实际情况去制定相关决策。同时，预先给定的灌溉目标表明，需要给予经济作物更多的关注，并适当压缩秋收作物的灌溉面积，从而实现节水高效农业的要求。本文得到的结果可为当地水资源管理和作物种植面积优化提供决策支持。

□

[1] 石敏俊, 王 磊, 王晓君. 黑河分水后张掖市水资源供需格局变化及驱动因素[J]. 资源科学, 2011,33(8):1 489-1 497.

[2] Cheng G, Li X, Zhao W, et al. Integrated study of the water-ecosystem-economy in the Heihe River Basin [J]. National Science Review, 2014,1(3):413-428.

[3] 李 茉, 郭 萍, 杨献献. 基于分式规划的种植结构多目标不确定性模型研究[J]. 节水灌溉, 2013,(9):79-81.

[4] Li Y P, Huang G H, Nie S L. An interval-parameter multi-stage stochastic programming model for water resources management under uncertainty [J]. Advances in Water Resources, 2006,29(5):776-789.

[5] Guo P, Huang G H. Two-stage fuzzy chance-constrained programming: application to water resources management under dual uncertainties [J]. Stochastic Environmental Research & Risk Assessment, 2009,23(3):349-359.

[6] Li W, Li Y P, Li C H, et al. An inexact two-stage water management model for planning agricultural irrigation under uncertainty [J]. Agricultural Water Management, 2010,97(11):1 905-1 914.

[7] 付银环, 郭 萍, 方世奇,等. 基于两阶段随机规划方法的灌区水资源优化配置[J]. 农业工程学报, 2014,30(5):73-81.

[8] 张 静, 黄国和, 刘 烨,等. 不确定条件下的多水源联合供水调度模型[J]. 水利学报, 2009,40(2):160-165.

[9] Zeng X, Kang S, Li F, et al. Fuzzy multi-objective linear programming applying to crop area planning [J]. Agricultural Water Management, 2010,98(1):134-142.

[10] 李 婷. 不确定性条件下基于水质模拟的流域水环境管理优化研究[D]. 北京：华北电力大学, 2013.

[11] 李小萌, 何 理, 卢宏玮. 基于模糊可信度约束的不确定性农业水资源规划模型研究[J]. 水资源与水工程学报, 2014,25(4):108-114.

[12] 陶子乐滔, 王 静, 蔡怡馨,等. 基于可信性规划的昆明市水资源优化配置模型[J]. 水电能源科学, 2015,30(7):30-33.

[13] 刘宝碇. 不确定规划及应用[M]. 北京：清华大学出版社, 2003.