条件非线性最优扰动(CNOP):简介与数值求解
孙国栋穆穆段晚锁王强彭飞
(1 中国科学院大气物理研究所,大气科学和地球流体力学数值模拟国家重点实验室,北京 100029;2 复旦大学大气科学研究院,上海 200433;3 中国科学院海洋研究所,海洋环流与波动重点实验室,青岛 266071;4 中国科学院大学,北京 100049)
条件非线性最优扰动(CNOP):简介与数值求解
孙国栋1,4穆穆2段晚锁1王强3彭飞1,4
(1 中国科学院大气物理研究所,大气科学和地球流体力学数值模拟国家重点实验室,北京 100029;2 复旦大学大气科学研究院,上海 200433;3 中国科学院海洋研究所,海洋环流与波动重点实验室,青岛 266071;4 中国科学院大学,北京 100049)
介绍了条件非线性最优扰动(Conditional Nonlinear Optimal Perturbation,CNOP)的定义及其在大气和海洋等可预报性研究中的应用。根据研究对象不同,CNOP分为与初始扰动有关的CNOP(CNOP-I)方法、与模式参数扰动有关的CNOP(CNOP-P)方法和同时考虑初始扰动和模式参数扰动的CNOP方法。目前,CNOP-I方法已经应用于ENSO、黑潮和阻塞可预报性以及热盐环流和草原生态系统稳定性的研究。此外,CNOP-I方法也被应用于探讨台风目标观测的研究,利用CNOP-I方法能够识别出台风预报的初值敏感区,通过观测系统模拟试验表明在初值敏感区增加观测能够有效改进台风的预报技巧。CNOP-P方法也在ENSO和黑潮可预报性以及热盐环流和草原生态系统稳定性研究中得到了应用。为了将CNOP方法应用于更多的领域,本文利用一个简单的Burgers方程,介绍了如何通过建立Burgers方程的切线性模式和伴随模式,从而利用非线性最优化算法计算获得CNOP。这一数值试验为将CNOP方法应用于更多的领域提供了借鉴。
条件非线性最优扰动方法(CNOP),可预报性,目标观测
0 引言
大气和海洋科学中的数值天气和气候可预报性研究一直是国内外研究的热点问题。很多方法已经建立并且应用去探讨数值天气和气候的可预报性问题。Leith[1]利用蒙特卡罗技术构建大量的随机初始误差,研究发现这些初始误差对6~10d的风场的预报技巧有较大改进。但是随机样本个数的选取是非常难以决定的,并且选取的初始误差是随机的。近些年,很多学者建立和应用一些方法探讨了数值天气和气候的可预报性,例如繁殖模向量和集合卡尔曼滤波方法等[2-3]。其中,一些产生动力约束的初始扰动的线性方法被建立去研究数值天气和气候可预报性。例如,线性奇异向量方法和Lyapunov向量方法等。这些方法已经被应用于研究海—气耦合模式中误差发展的有关规律[4-5]。这些方法属于初始误差发展的线性理论[6]。只有在时间较短和初始误差较小的情况下,线性近似才是成立的。然而,大气和海洋科学中的物理问题通常是非线性问题。随着初始误差的时间演变,将线性误差理论应用于非线性问题的研究是不合适的。建立非线性误差理论对研究大气和海洋科学中的非线性问题是非常必要的。Mu等[7-8]为了克服线性奇异向量方法的线性局限性,提出了条件非线性最优扰动(Conditional Nonlinear Optimal Perturbation, CNOP)方法。CNOP方法是线性奇异向量方法在非线性框架下自然的扩展。CNOP方法的建立对研究大气和海洋科学的可预报性问题提供了有力的工具。
1 CNOP的定义
CNOP是在一定误差范围内,在预报时刻对预报结果不确定性产生最大影响的误差。根据大气和海洋科学可预报性的分类[9],Mu等[7]建立了研究第一类可预报性问题的方法,与初始误差有关的CNOP方法,记为CNOP-I方法。根据第二类可预报性问题,Mu等[8]建立了与初始误差和模式误差都有关的CNOP方法,其中与模式误差有关的CNOP方法记为CNOP-P方法。具体地,假设一个非线性动力系统:
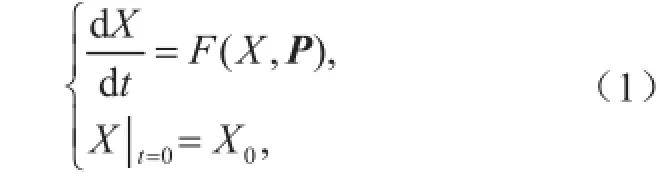
式中,X0表示状态变量X的初始状态。表示模式参数向量,m代表式(1)中参数的个数,F是一个非线性微分算子。在离散状态下,式(1)在T时刻的解可以表示为:
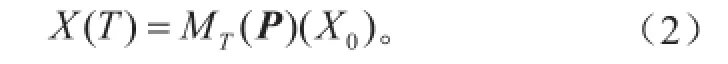
这里MT(P)是在固定参数向量P时的非线性传播算子,它将初始时刻的状态X0“传播”到T时刻的状态X (T)。
用U0表示模式初值,u0表示模式的初始误差,表示模式参数误差,根据式(2),模式的解可写为如下形式:

式中,度量了由联合误差导致状态变量在T时刻偏离参考态U(T)的大小。
假设只考虑初始误差u0,不考虑模式的参数误差,即 =0,根据式(3),我们能获得它所对应的T时刻的解U(T) +u(T) ,即有:
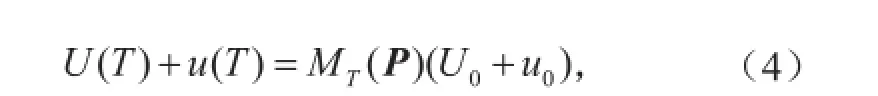
式中u(T)为该初始误差的非线性发展。
假设只考虑模式参数误差 ,不考虑模式的初始误差,即u0=0,那么模式的解可写为如下形式:
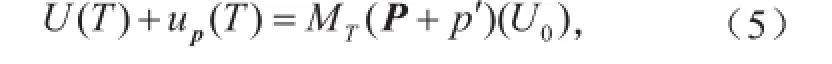
式中up(T)度量了由参数误差导致状态变量在T时刻偏离参考态U(T)的大小。
定义如下的非线性最优化问题:
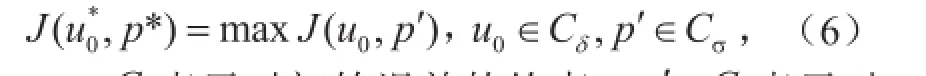
式中,表示对初始误差的约束,表示对参数误差的约束,并且
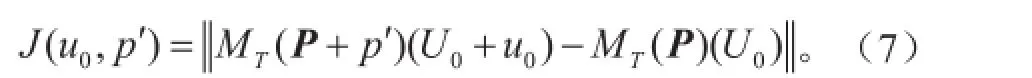
显然,最优化问题式(6)是一个有约束的最优化问题。对于给定的范数,式(6)中最优化问题的解()为最优的初始误差和参数误差,表示在一定误差约束条件下,在T时刻使得目标函数J偏离参考态程度最大。可以看到,当我们仅仅考虑初始误差或者假设参数误差 =0,最优化问题式(6)变为:
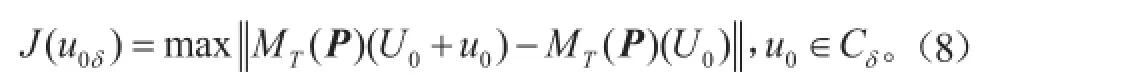
并且满足式(8)的初始误差u0δ就是CNOP-I,即为Mu等[7]定义的CNOP。如果在式(8)中用切线性模式的传播算子代替MT,那么满足式(8)式的初始误差就是线性奇异向量(Linear Singular Vector, LSV),因此,CNOP方法是LSV方法在非线性框架下自然地推广。
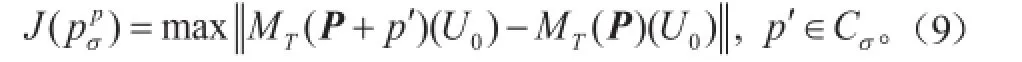
若在式(6)中我们不考虑初始误差,即u0=0,可以得到:式中,是与参数有关的条件非线性最优扰动。类似于CNOP-I,称这样的最优参数误差为CNOP-P。这样可以明确地看到式(6)中的最优联合模态是CNOP-I和CNOP-P的扩展(Mu等[8])。
2 CNOP方法的应用
近些年,CNOP方法已经被应用于研究大气和海洋科学中的一些物理问题[10]。例如,Mu等[11-12]探讨了ENSO的可预报性和春季预报障碍问题(Spring Predictability Barrier, SPB)。研究结果表明CNOP型初始误差有明显的季节依赖性,在El Niño事件的不同发展阶段,CNOP型初始误差都会导致SPB。尽管LSV型初始误差的发展也有季节依赖性,但在各个季节的增长率远远小于CNOP型初始误差导致的预报误差的增长率,这体现了CNOP和LSV间的差异[13-14]。Mu等[15]在热盐环流的非线性变化方面也进行了探索。研究结果指出通过对流过程,初始误差的非线性作用导致了非对称的响应。Jiang等[16]将CNOP方法也应用于集合预报的研究,结果表明由CNOP方法生成的集合样本对中期集合预报的技巧高于由线性奇异向量方法。近些年,有一些学者将CNOP方法应用于台风目标观测的研究中。Mu等[17]研究结果表明用CNOP方法确定的敏感区进行目标观测对台风预报的改善程度大于用LSV确定的敏感区[18]。Terwiss-cha van Scheltinga等[19]用CNOP方法研究了正压模式中双环流的非线性变化,结果表明当雷诺数达到一定数值后,双环流的非对称且线性稳定的状态将变为非线性不稳定性的。上述研究属于第一类可预报性研究范畴。为了研究第二类可预报性问题,Duan等[20]用CNOP-P方法研究了ENSO事件的SPB现象。CNOP-P方法也在陆地生态系统变化研究中进行了应用。Sun等[21-23]将温度和降水视为外强迫型参数,应用CNOP-P方法研究了温度和降水变化情况下,中国区域陆地生态系统变化的对外强迫最大响应。结果表明在干旱和半干旱区域以及南方区域,陆地生态系统的响应较为明显。
上述研究只是针对单独考虑初始扰动或者模式参数扰动。近些年,一些研究同时考虑初始扰动和参数扰动。Wang等[24]用CNOP方法考察了模式参数误差对黑潮路径变异的影响,结果表明,尽管初始误差导致的黑潮路径变异的预报误差大于模式误差导致的预报误差,但是模式误差对黑潮路径变异的影响不容忽视。Yu等[25]利用Zebiak-Cane模式分析了初始误差和模式误差在导致显著春季预报障碍中所扮演的角色。数值结果表明在导致显著春季预报障碍中,初始误差比模式误差更重要。Sun等[26]利用CNOP方法研究了草原生态系统的稳定性,结果表明在不同强度人类活动情况下,对草原生态系统模拟不确定性影响最大(即发生突变)的气候变化类型是不相同的。这意味着气候变化的模态对于草原生态系统的维持或退化是非常重要的,同时告诉我们应该合理地利用草原生态系统。上述这些研究说明了CNOP方法在大气和海洋科学的非线性问题的研究中是一个有效的工具。
3 CNOP的数值求解
计算CNOP是一个求解有约束条件的非线性最优化问题的过程。如何计算这个非线性最优化问题是应用CNOP方法研究大气和海洋科学的非线性物理问题的关键之处。我们以计算CNOP-I这个非线性最优化问题为例,计算CNOP-P与其是类似的。计算CNOP-I就是利用合适的最优化算法求解式(8)。事实上,已有很多较为成熟的最优化算法能够求解公式(8)。序列二次规划(Sequential Quadratic Programming, SQP,Barclay等[27])算法﹑谱投影梯度(Spectral Projected Gradient, SPG,Birgin等[28])算法和Limitedmemory Broyden-Fletcher-Goldfarb-Shanno(L-BFGS, Liu等[29])方法等都是求解有约束的非线性最优化问题的最优化算法。如果能够将目标函数﹑目标函数关于优化变量的梯度和约束条件准确地输入到非线性最优化算法中,就可以通过计算得到CNOP-I。
目标函数﹑目标函数关于优化变量的梯度和约束条件需要使用者定义并且输入到非线性最优化程序中(图1)。首先,物理问题的约束条件可以较为容易地在约束优化算法中建立。有些约束优化算法也需要约束条件关于优化变量的梯度,例如SQP算法。这也可以较为容易地建立。其次,在优化算法中,需给出正确的目标函数值。式(7)中算子MT代表一个非线性模式从初始时刻到预报时刻T的传播算子。为了得到目标函数,需要将非线性模式向前积分的信息输入到优化算法中。即优化算法程序需要调用两次模式的数值积分程序:一次是参考态(或基本态)MT(P) (U0),此时并未考虑初始误差;一次是考虑初始误差时的非线性积分MT(P) (U0+u0)。将这两次非线性积分的结果输入到优化算法程序中,从而获得目标函数。最后,目标函数关于优化变量的梯度是应用约束优化算法计算CNOP中非常重要的信息,它也是能否找到最优值的关键。定义法是求梯度最基本的方法。这种方法对理论模型是非常有效的。然而对于大气和海洋科学中的海-气耦合模式,由于该模式包含了较为复杂的动力框架和物理过程,用定义法求梯度的计算量非常大。对于大气和海洋科学中的数值模式,获得目标函数梯度的另一种技术是伴随技术。在这里,我们不介绍伴随技术。利用向前积分模式﹑其切线性模式和伴随模式,可以获得目标函数关于优化变量的梯度,将梯度信息输入到约束优化算法中,即优化算法程序中需要调用向前积分模式﹑其切线性模式和伴随模式三个程序。至此,上述三个信息输入到约束优化算法中并且给出初始猜测值,算法就能正常运行并最终得到CNOP-I。
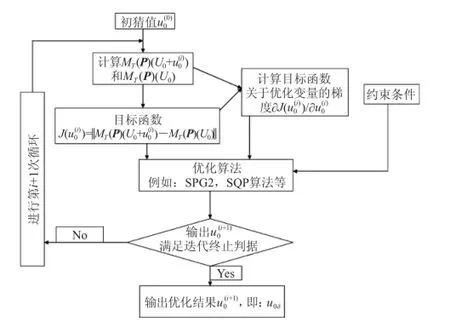
图1 计算CNOP的流程图Fig. 1 The flow chart to calculate CNOP
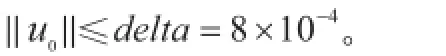
1)Burgers方程
Burgers方程如下所示:
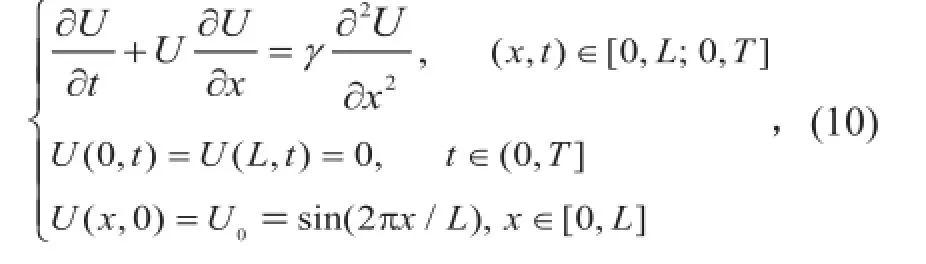
它描述了状态变量U随时间的变化。在这里,γ=0.005m2/s,L=100m,T=30s。我们使用中心有限差分方法对式(10)进行离散化,得到了Burgers方程的数值积分模式,空间步长和时间步长分别是Δx=1.0m(空间格点总数目nx=101)、Δt=1.0s。然后在此基础之上,写出方程的切线性模式和伴随模式(为了求目标函数关于优化变量的梯度)。使用Fortran进行编程,在附录中我们给出了各模式的程序[30]。
2)切线性模式、伴随模式以及梯度计算检验
在积分伴随模式求目标函数关于优化变量的梯度之前,一般要对切线性模式、伴随模式以及所得的梯度进行检验,从而保证实际应用中所得的结果与理论分析相符合。下面将分别给出这三部分的检验结果。需要说明的是:以下数值结果都是在变量和参数取双精度的情况下得到的;各部分中扰动u0的取值都是u0(i)=Δ×i×0.01×(-1)i(i=1,…, nx-2)。Δ表示优化问题中的约束半径。
① 切线性模式程序检验结果
根据切线性模式的定义,对所建立的切线性模式程序是否正确可以采用以下公式进行检验:
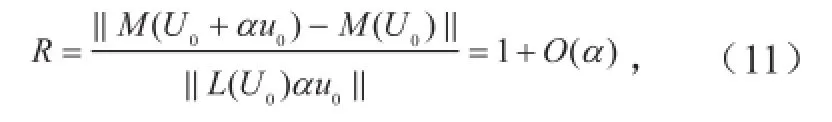
式中,M表示非线性模式,L表示M的切线性模式,表示取欧氏范数,u0是U0的扰动,0<α<1。某一基态下,切线性模式程序检验结果如表1所示。由此可知,当α趋于0时,R一致的逼近于1。这说明切线性模式的程序非常准确。
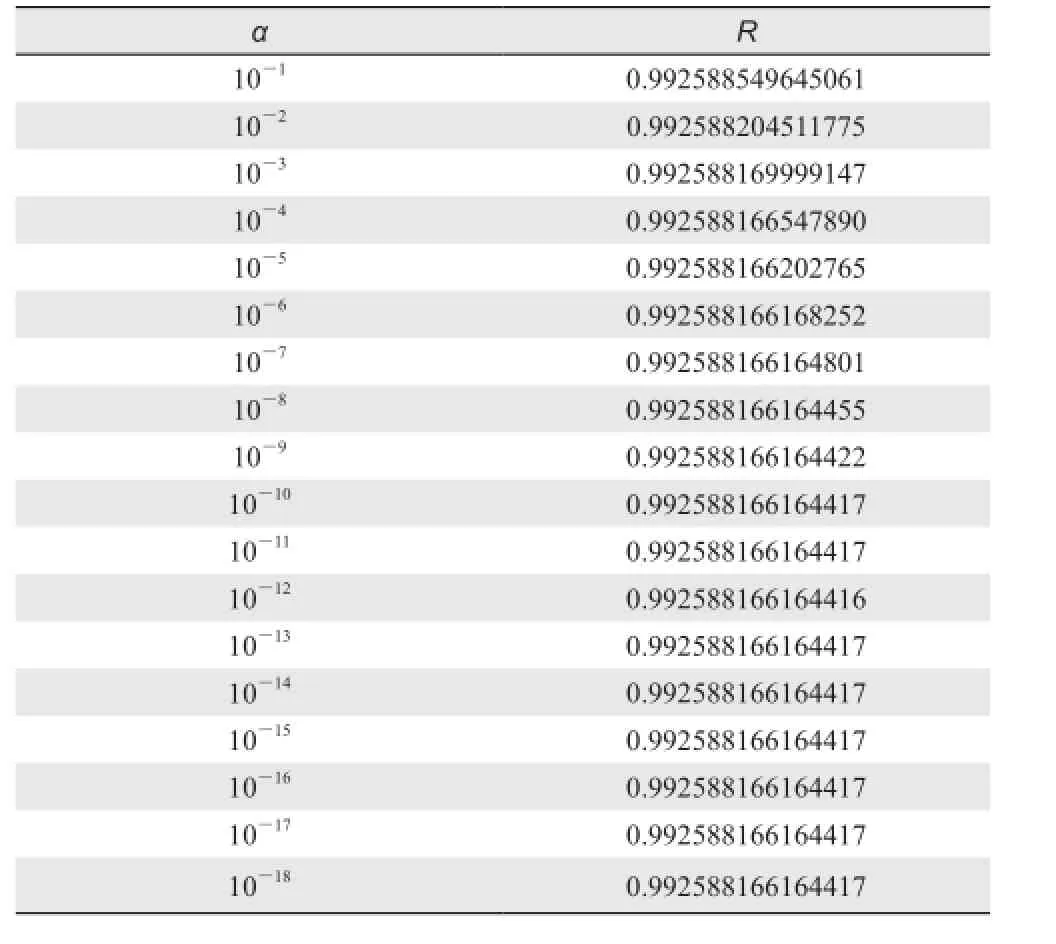
表1 切线性模式的检验结果Table1 The results of the tangent linear model
② 伴随模式程序检验结果
根据伴随算子的定义,伴随模式程序的检验公式如下:
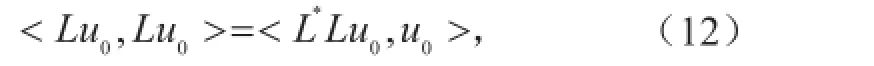
式中,L表示切线性模式,L*表示伴随模式,u0代表扰动。
依照式(12),以u0为初值,积分切线性模式,将结果和其自身作内积,记作Valtlm。然后以Lu0为初值,积分伴随模式,将结果和u0作内积,记作Valadj。最后在机器精度的标准下,检验Valtlm=Valadj是否成立。某一基态下,伴随模式检验结果如表2所示。

表2 伴随模式的检验结果Table2 The results of the adjoint model
由表2可知,Valtlm和Valadj相等的有效数字达到15位,非常接近机器精度(16位有效数字),这说明从切线性模式程序出发建立的伴随模式程序是准确的。
③ 梯度计算检验结果
根据定义,梯度计算的检验公式如下:
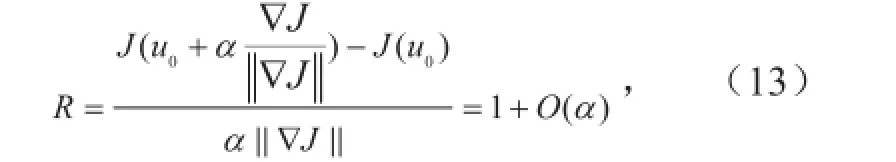
式中,J(u0)是目标函数,是由伴随程序计算的J在扰动u0处的梯度表示取欧氏范数,0<α<1。梯度的检验结果如表3所示。由表可知,当α趋于0时,R在1附近呈现抛物型结构,这说明伴随模式可用于求解优化问题中代价函数的梯度。
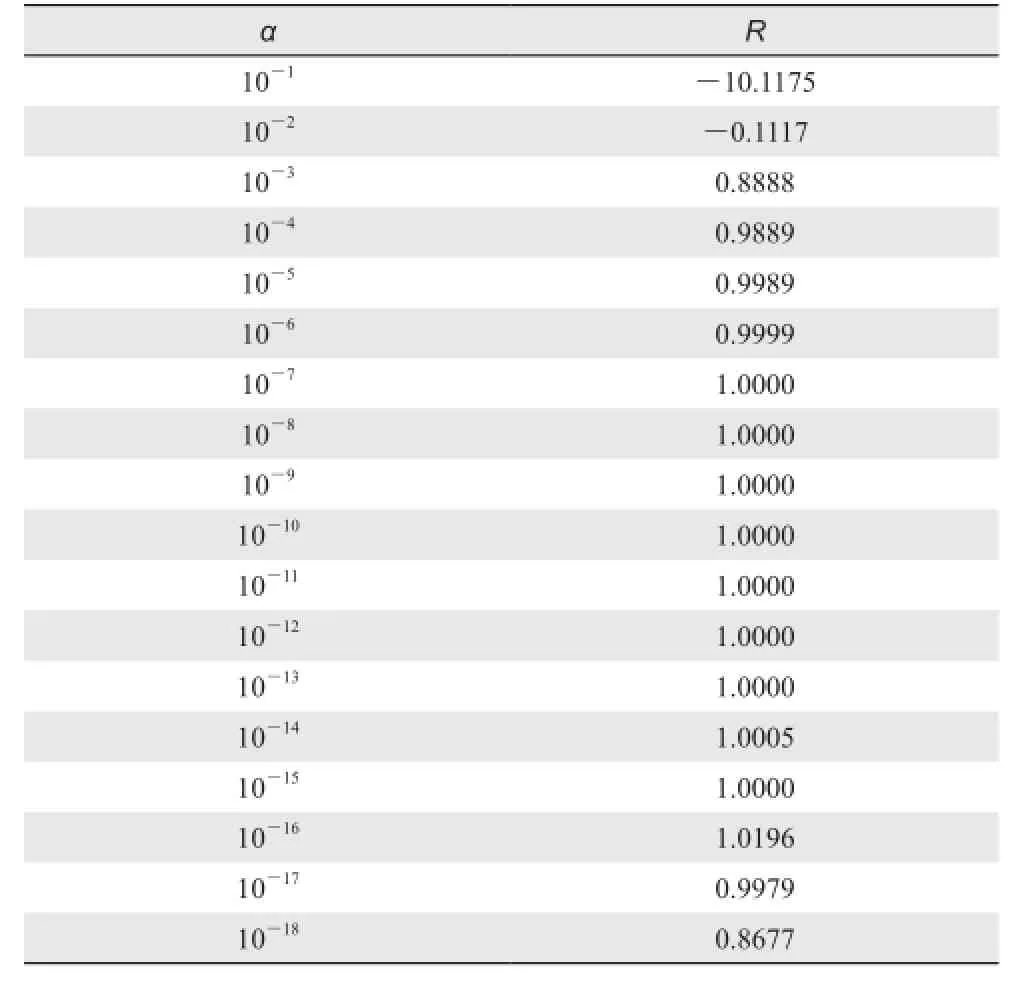
表3 梯度计算的检验结果Table3 The results of gradients
3)计算结果
图2是当Burgers方程中初始条件为U0时,状态变量U随时间的发展,也是我们求解CNOP时的基态,也可以称其为参考态,即式(7)中MT(P) (U0)。
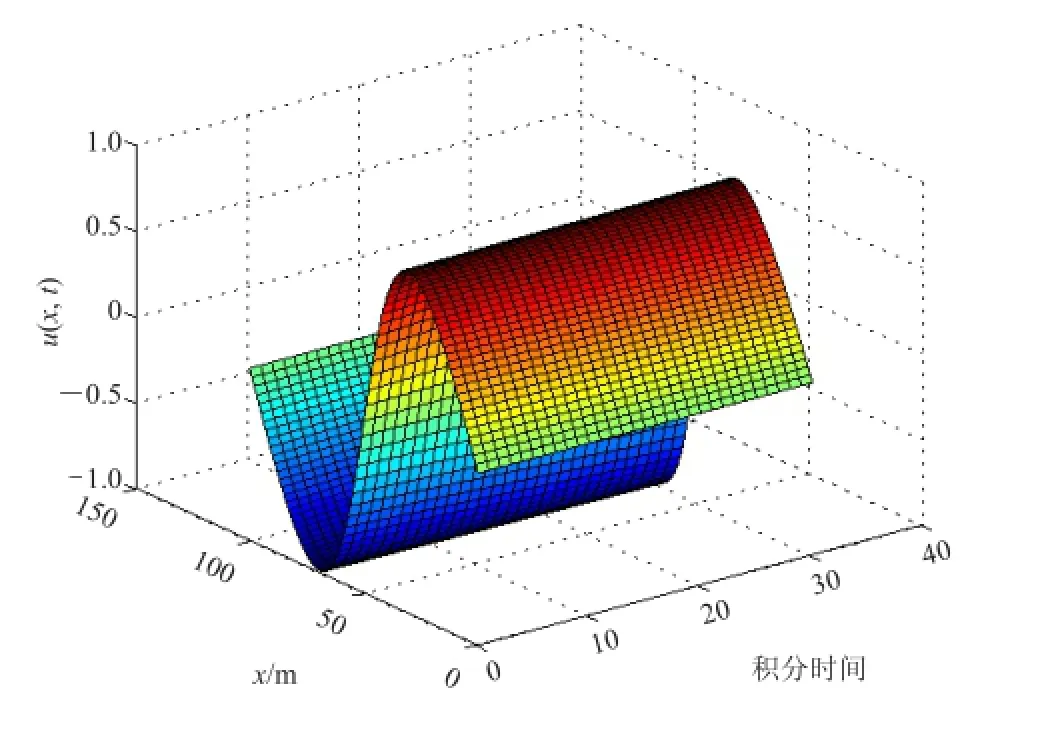
图2 初始条件为U0时状态变量U的非线性发展Fig. 2 The nonlinear evolution of the state variableUwhen the initial condition isU0
在求解目标函数J(u0)最小值和最小值点(CNOP)时,我们使用的优化算法是SPG2,该算法需要使用目标函数的梯度信息。下面分别使用定义法和伴随方法获取目标函数的梯度,进而求得CNOP,并且比较两种方法得到的CNOP有何差异。
如图3所示,两种方法所得到的CNOP空间分布极其相似。图4是两个CNOP差异的空间分布。由上可知,基于伴随方法得到的CNOP和基于定义方法得到的CNOP几乎是一样的,而且两者随时间的发展也几乎一样,如图5所示。综上可知,两种方法得到的CNOP几乎一样。然而基于伴随求CNOP的方法所使用的CPU时间远远小于基于定义求CNOP的方法所使用的CPU时间(图5)。因而,基于伴随求CNOP的方法准确而且效率高。图6给出了CNOP非线性发展的时空分布。由此看到在时刻T,CNOP类型初始扰动有最大非线性发展。
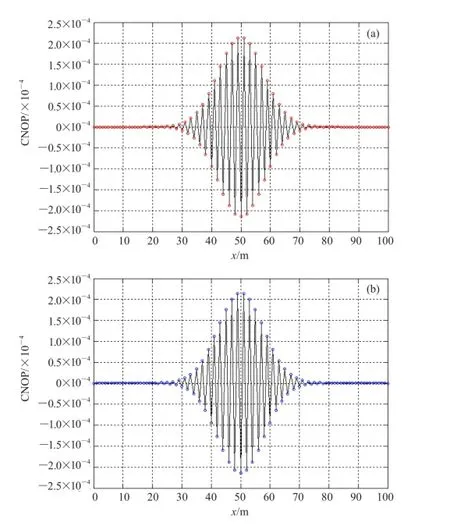
图3 CNOP的空间分布(a)基于伴随方法;(b)基于定义方法Fig. 3 The spatial distribution of CNOP(a)The adjoint method;(b)The definition method
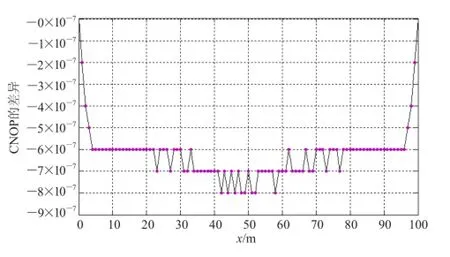
图4 基于伴随方法和定义方法计算得到的CNOP的差异Fig. 4 The difference of CNOP obtained by the adjoint method and the definition method
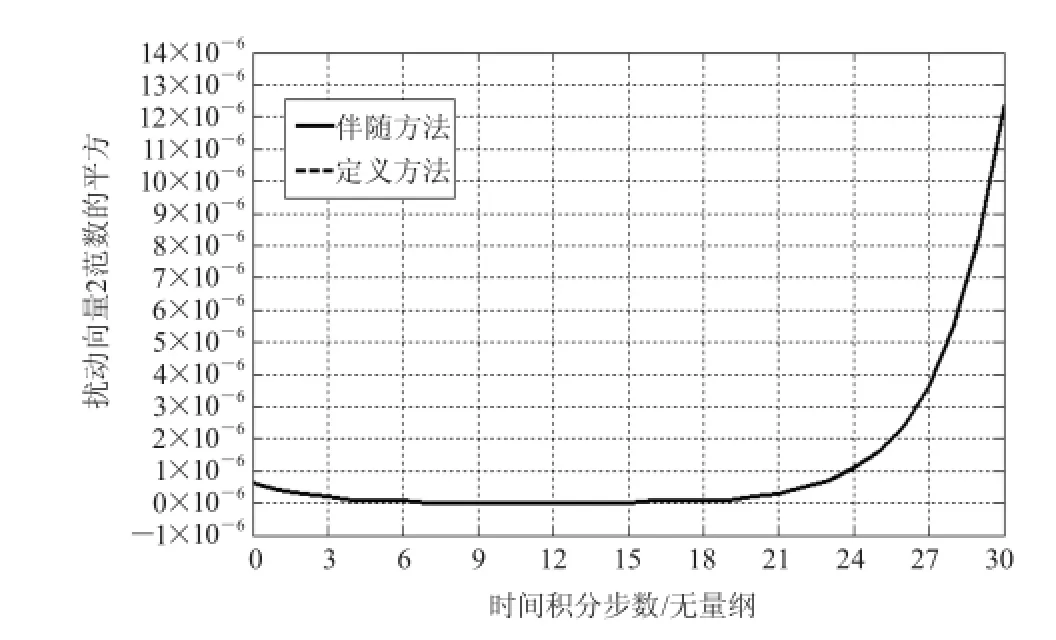
图5 基于伴随方法和定义方法的CNOP的非线性发展Fig. 5 The nonlinear evolution of CNOP obtained by the adjoint method and the definition method
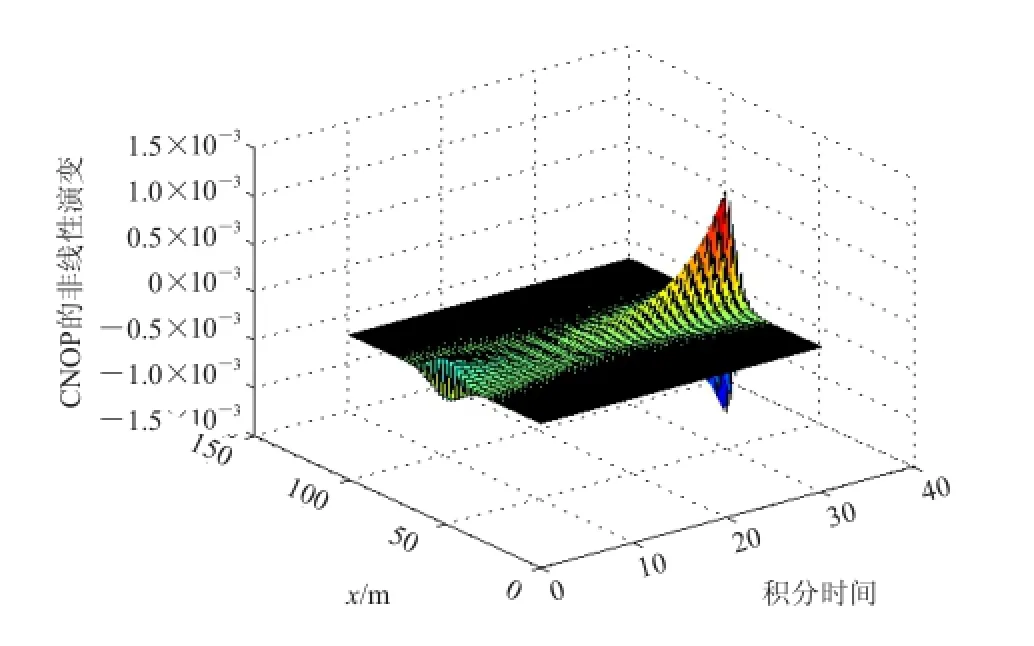
图6 CNOP非线性演变的时空分布特征Fig. 6 The spatial and temporal difference of the nonlinear evolution of CNOP
4 结论和讨论
天气和气候的可预报性问题是目前科学研究的热点问题之一。传统的LSV方法在研究天气和气候的可预报性问题上具有局限性,因为此方法是假设天气和气候事件的演变过程是线性的。为了扩展LSV方法的局限性,Mu等[7-8]建立了CNOP方法。本文不仅介绍了CNOP的定义和拓展CNOP等定义,并且详细地介绍了CNOP方法在ENSO、黑潮和阻塞可预报性,以及热盐环流和草原生态系统稳定性研究中的应用。
特别地,为了让更多的学者能够应用CNOP方法并将其应用于更多的研究领域,本文利用一个理论的Burgers方程,详细地介绍了如何建立此方法的积分模式、切线性模式和伴随模式[30],通过介绍计算CNOP的流程图,尝试让学者了解如何利用非线性最优化算法计算CNOP。本文只是介绍了与初始扰动有关的CNOP的计算,如果计算CNOP-P,可以参考Mu等[8]的研究。从本文的介绍可以看出,计算CNOP需要积分模式对应的切线性模式和伴随模式。然而,目前有些海-气耦合模式缺乏相应的切线性模式和伴随模式。为了能使CNOP方法得到更广泛的应用,一些学者[31-32]利用集合投影方法近似计算梯度信息,从而避免了需要积分模式对应的切线性模式和伴随模式而获得梯度信息。这为CNOP方法的应用提供了一种可行的途径。
[1]Leith C E. Theoretical skill of Monte Carlo forecast. Mon Wea Rev, 1974, 102: 409-418.
[2]Houtekamer P L, Lefaivre L, Derome J, et al. A system simulation approach to ensemble prediction. Mon Wea Rev, 1996, 124: 1225-1242.
[3]Toth Z, Kalnay E. Ensemble forecasting at NCEP: the breeding method. Mon Wea Rev, 1997, 125: 3297-3318.
[4]Buizza R, Palmer T. Potential forecast skill of ensemble prediction, and spread and skill distributions of the ECMWFensemble prediction system. Mon Wea Rev, 1997, 125: 99-119.
[5]Hamill T M, Snyder C, Morss R E. A comparison of probabilistic forecasts from bred, singular-vector, and perturbed observation ensembles. Mon Wea Rev, 2000, 128: 1835-1851.
[6]Garcia-Moya J A, Callado A, Escriba P, et al. Predictability of short-range forecasting: a multimodel approach. Tellus A, 2011, 63: 550-563.
[7]Mu M, Duan W S, Wang B. Conditional nonlinear optimal perturbation and its applications. Nonlin Processes Geophys , 2003, 10: 493-501.
[8]Mu M, Duan W S, Wang Q, et al. An extension of conditional nonlinear optimal perturbation approach and its applications. Nonlin Processes Geophys, 2010, 17: 21-220. doi:10.5194/ npg-17-211-2010.
[9]Mu M, Duan W S, Wang J C. The predictability problems in numerical weather and climate prediction. Adv Atmos Sci, 2002, 19(2): 191-204.
[10]穆穆,段晚锁.2013.条件非线性最优扰动在可预报性问题研究中的应用.大气科学,37(2):281-296. doi:10.3878/ j.issn.1006-9895.2012.12319.
[11]Mu M, Duan W S, Wang B. Season-dependent dynamics of nonlinear optimal error growth and El Niño-Southern Oscillation predictability in a theoretical model. J Geophys Res, 2007, 112, D10113. doi:10.1029/2005JD006981.
[12]Mu M, Xu H, Duan W S. A kind of initial errors related to “spring predictability barrier” for El Niño events in Zebiak-Cane model. Geophys Res Lett, 2007, 34, L03709. doi:10.1029/2006GL027412.
[13]Duan W S, Xu H, Mu M. Decisive role of nonlinear temperature advection in El Niño- and La Niña- amplitude asymmetry. J Geophys Res, 2008, 113, C01014. doi:10.1029/2006JC003974.
[14]Mu M, Duan W S, Wang J F. Nonlinear optimization problems in atmospheric and oceanic sciences. East-west J Math, Thailand, 2002, (S): 155-164.
[15]Mu M, Sun L, Dijikstra H A. The sensitivity and stability of the ocean’s thermohaline circulation to fi nite amplitude perturbations. J Phys Oceanogr, 2004, 34: 2305-2315.
[16]Jiang Z N, Mu M. A comparisons study of the methods of conditional nonlinear optimal perturbations and singular vectors in ensemble prediction. Adv Atmos Sci, 2009, 26(3): 465-470. doi: 10.1007/s00376-009-0465-6.
[17]Mu M, Zhou F F, Wang H L. A method for identifying the sensitive areas in targeted observations for tropical cyclone prediction: conditional nonlinear optimal perturbation. Mon Wea Rev, 2009, 137: 1623-1639.
[18]Qin X, Mu M. Influence of conditional nonlinear optimal perturbations sensitivity on typhoon track forecasts. Quart J Roy Meteor Soc, 2011, 138: 185-197.
[19]Terwisscha van S A D, Dijkstra H A. Conditional nonlinear optimal perturbations of the double-gyre ocean circulation. Nonlin Processes Geophys, 2008, 15: 727-734. doi:10.5194/npg-15-727-2008.
[20]Duan W S, Zhang R. Is model parameter error related to a signi fi cant spring predictability barrier for El Nino events? Results from a theoretical model. Adv Atmos Sci, 2010, 27(5): 1003-1013.
[21]Sun G D, Mu M. Responses of soil carbon variation to climate variability in China using the LPJ model. Theoretical and Applied Climatology, 2012, 110:143-153. doi:10.1007/s00704-012-0619-9. [22]Sun G D, Mu M. Understanding variations and seasonal characteristics of net primary production under two types of climate change scenarios in China using the LPJ model. Climatic Change, 2013, 120:755-769.doi: 10.1007/s10584-013-0833-1.
[23]Sun G D, Mu M. The analyses of the net primary production due to regional and seasonal temperature di ff erences in eastern China using the LPJ model. Ecological Modelling, 2014, 289: 66-76. doi: 10.1016/j.ecolmodel.2014.06.021.
[24]Wang Q, Mu M, Dijkstra H A. Application of the conditional nonlinear optimal perturbation method to the predictability study of the Kuroshio large meander. Adv Atmos Sci, 2012, 29(1): 118-134. doi: 10.1007/s00376-011-0199-0.
[25]Yu Y S, Mu M, Duan W S. Does Model Parameter Error Cause a Signi fi cant “Spring Predictability Barrier” for El Niño Events in the Zebiak–Cane Model? J Climate, 2012, 25: 1263-1277. doi: http://dx.doi.org/10.1175/2011JCLI4022.1
[26]Sun G D, Mu M. Inducing unstable grassland equilibrium states due to nonlinear optimal patterns of initial and parameter perturbations: theoretical models. Adv Atmos Sci, 2012, 29(1): 79-90. doi: 10.1007/s00376-011-0226-1.
[27]Barclay A, Gill P E, Rosen J B. SQP methods and their application to numerical optimal control. Numerical Analysis Report 97-3, Department of Mathematics, University of California, San Diego, La Jolla, CA, 1997.
[28]Birgin E G, Martinez J M, Raydan M. Nonmonotone spectral projected gradient methods on convex sets. SIAM J Optimization, 2000, 10(4): 1196-1211.
[29]Liu D C, Nocedal J. On the limited memory BFGS method for large scale minimization. Math Prog, 1989, 45: 503-528.
[30]Kalnay E. Atmospheric Modeling, Data Assimilation, and Predictability. Cambridge: Cambridge University Press, 2003.
[31]Wang B, Tan X W. Conditional nonlinear optimal perturbations: adjoint-free calculation method and preliminary test. Mon Wea Rev, 2010, 138: 1043-1049
[32]Chen L, Duan W S, Xu H. A SVD-based ensemble projection algorithm for calculating conditional nonlinear optimal perturbation. Sci China: Earth Sci,2014,58 :385-394. doi: 10.1007/ s11430-014-4991-4.
附录1 Burgers方程的数值积分模式、切线性模式和伴随模式
1)数值积分模式
SUBROUTINE BURGER(nx,n,ui,ub,u)
implicit none
integer nx !number of grid points
integer n !number of time steps
double precision ub(nx,n) !basic states(u)
double precision u(nx,n) !model solutions
double precision ui(nx) !initial conditions
double precision dx !space increment
double precision dt !time increment
double precision gamma ! diffusion coeff i cient
double precision c0,c1
integer i,j
common /com_param/ c0,c1
gamma=0.005d0
dx=0.01d0
dt=0.001d0
c0=dt/dx
c1=gamma*dt/(dx**2)
!set the initial conditions:
do i=1,nx
u(i,1)=ui(i)
end do
!set the boundary conditions:
do j=1,n
u(1,j)=0.
u(nx,j)=0.
end do
!integerate the model numerically:-----use central fi nite difference method on spatial and temporal directions
do i=2,nx-1
u(i,2)=u(i,1)-0.25*c0*(u(i+1,1)*u(i+1,1)-u(i-1,1)*u(i-1,1))+c1*(u(i+1,1)+u(i-1,1)-2*u(i,1))
end do
do j=3,n
do i=2,nx-1
u(i,j)=u(i,j-2)-0.5*c0*(u(i+1,j-1)*u(i+1,j-1)-u(i-1,j-1)*u(i-1,j-1))+2*c1*(u(i+1,j-1)+u(i-1,j-1)-2*u(i,j-1))
end do
end do
!save the nonlinear solutions to the basic fi elds:
do j=1,n
do i=1,nx
ub(i,j)=u(i,j)
end do
end do return
END SUBROUTINE
2)切线性模式
SUBROUTINE BURGER_TLM(nx,n,ui,ub,u)
implicit none
integer nx,n
double precision ub(nx,n) !basic state
double precision u(nx,n) !TLM solutions
double precision ui(nx) !initial conditions
common /com_param/ c0,c1
double precision c0,c1
integer i,j
! set the initial conditions
do i=1,nx
u(i,1)=ui(i)
end do
! set the bundary conditions:
do j=1,n
u(1,j)=0.
u(nx,j)=0.
end do
! integer the model numerically:
do i=2,nx-1
u(i,2)=u(i,1)-0.5*c0*(ub(i+1,1)*u(i+1,1)-ub(i-1,1)*u(i-1,1))+c1*(u(i+1,1)+u(i-1,1)-2*u(i,1))
end do
do j=3,n
do i=2,nx-1
u(i,j)=u(i,j-2)-c0*(ub(i+1,j-1)*u(i+1,j-1)-ub(i-1,j-1)*u(i-1,j-1))+2*c1*(u(i+1,j-1)+u(i-1,j-1)-2*u(i,j-1))
end do
enddo
! set the fi nal value of u in ui
do i=1,nx
ui(i)=u(i,n)
end do
return
END SUBROUTINE
3) 伴随模式
SUBROUTINE BURGER_ADJ(nx,n,ui,ub,u)
implicit none
integer nx,n
double precision ub(nx,n) !basic states
double precision u(nx,n) !modle solutions
double precision ui(nx) !initial conditions
double precision dt !time increment
double precision dx !space increment
double precision c0,c1
integer i,j
common /com_param/ c0,c1
!initialize adjoint variables:
do j=1,n
do i=1,nx
u(i,j)=0.
end do
end do
!set the fi nal conditions:
do i=1,nx
u(i,n)=ui(i)
ui(i)=0.
end do
do j=n,3,-1
do i=nx-1,2,-1
u(i,j-2)=u(i,j-2)+u(i,j)
u(i-1,j-1)=u(i-1,j-1)+(2*c1+c0*ub(i-1,j-1))*u(i,j)
u(i,j-1)=u(i,j-1)-4*c1*u(i,j)
u(i+1,j-1)=u(i+1,j-1)+(2*c1-c0*ub(i+1,j-1))*u(i,j)
u(i,j)=0
end do
end do
do i=nx-1,2,-1
u(i-1,1)=u(i-1,1)+(c1+0.5*c0*ub(i-1,1))*u(i,2)
u(i,1)=u(i,1)+(1-2*c1)*u(i,2)
u(i+1,1)=u(i+1,1)+(c1-0.5*c0*ub(i+1,1))*u(i,2) u(i,2)=0
end do
!set the boundary conditions:
do i=1,n
u(1,i)=0.0
u(nx,i)=0.
end do
!set the fi nal value of u in ui:----Gradent
do i=1,nx
ui(i)=ui(i)+u(i,1)
end do
return
END SUBROUTINE
附录2 谱投影梯度(SPG2)算法简介
谱投影梯度(Spectral Projected Gradient Method,SPG2)是一种非单调梯度投影算法,用于解决大规模的、可行域是凸集的优化问题(Birgin 等)[A1]。这种优化问题具有如下形式:
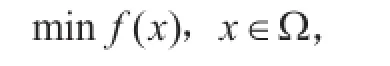
式中,Ω是Rn中的闭凸集,而且目标函数f在包含Ω的开集上具有连续偏导数。
需要说明的是,对于任意的,定义是与给定范数有关的在闭凸集Ω上的投影。g(x)表示目标函数的梯度,即。该算法以任意的开始。整数m表示算法中存储的目标函数值的最大个数;αmin是一个小参数,并且大于0;αmax是一个大参数,αmax>αmin;,代表一个足够小的参数;参数σ1,σ2满足:0<σ1<σ2<1;表示内积。SPG2算法具体如下:
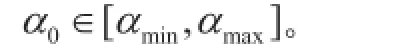
Step1 计算谱投影梯度。检验算法终止准则是否满足。如果满足,算法结束,xk即为最小值点;否则执行Step2。
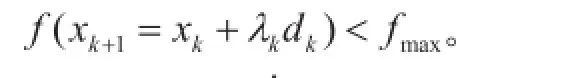
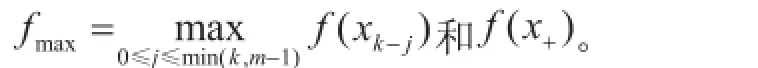
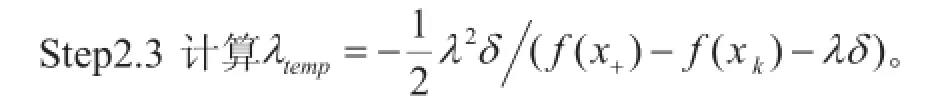
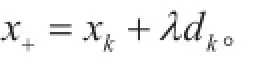
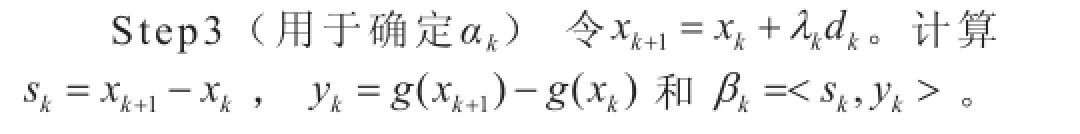
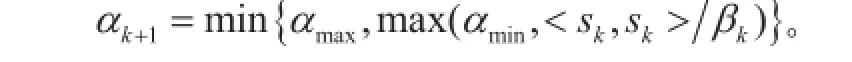
Step4 迭代次数k=k+1。进行Step1。
在SPG2优化算法中,收敛准则是:或者,其中ε1,ε2都是很小的数。如果收敛准则满足,则算法终止。此外,如果迭代次数k超过了给定的最大迭代次数maxit,或者目标函数值的计算次数超过了给定的最大计算次数maxfun,则算法同样会终止。此外,需要注意的是这个算法中目标函数值和目标函数的梯度需要由使用者给出。
参考文献
[A1] Birgin E G, Martinez J M, Raydan M. SPG: software for convexconstrained optimization. ACM Trans Math Softw, 2001, 27(3):340-349.
Conditional Nonlinear Optimal Perturbation: Introduction and Numerical Computation
Sun Guodong1,4, Mu Mu2, Duan Wansuo1, Wang Qiang3, Peng Fei1,4
(1 State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics (LASG), Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029 2 Institute of Atmospheric Sciences, Fudan University, Shanghai 200433 3 Key Laboratory of Ocean Circulation and Wave, Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071 4 University of Chinese Academy of Sciences, Beijing 100049)
This paper introduces the def i nition of conditional nonlinear optimal perturbation (CNOP), and the applications of the CNOP in atmosphere and ocean studies. The CNOP approach is expanded as that related to initial perturbation (CNOP-I), related to parameter perturbation (CNOP-P), and the combined both of CNOP-I and CNOP-P, according to the different perturbation types. The CNOP-I approach has been applied to the predictability studies of ENSO events, Kuroshio path anomalies, blocking, nonlinear stabilities of thermohaline circulation and grassland ecosystem. The CNOP-I has been further employed to explore the target observation of typhoon. The sensitive region could be identif i ed by using the CNOP-I approach. The forecast skill may be improved by adding more adaptive observations in the sensitive region. The CNOP-P approach has been applied also to Kuroshio path anomalies, nonlinear stabilities of thermohaline circulation and grassland ecosystem. Here, we carried out a numerical simulation how to obtain the CNOP with the Burgers equation through building the tangent linear model and adjoint model. The result shows that the CNOP can be calculated by using the Burgers equation, the tangent linear model and the adjoint model with nonlinear optimization algorithm; It supplies a guide to a beginner to learn the CNOP and a reference for employing the CNOP to other applicable subjects.
conditional nonlinear optimal perturbation (CNOP), predictability, adaptive observations
10.3969/j.issn.2095-1973.2016.06.001
2014年10月23日;
2015年3月31日
孙国栋(1980 —),Email: sungd@mail.iap.ac.cn
资助信息:国家自然科学基金(41375111,91437111)
 Advances in Meteorological Science and Technology2016年6期
Advances in Meteorological Science and Technology2016年6期
- Advances in Meteorological Science and Technology的其它文章
- 榜单
- SVM方法在霾识别和能见度预报中的应用
- 认识碳卫星
- 数字
- 媒体扫描MEDIA SCAN
- 风电功率组合预测技术研究综述
