磁力张量数据的目标体边界识别方法探讨

秦秀颖， 鲁光银， 朱自强， 曹书锦

(中南大学　地球科学与信息物理学院，长沙　410083)



磁力张量数据的目标体边界识别方法探讨

秦秀颖， 鲁光银， 朱自强， 曹书锦

(中南大学地球科学与信息物理学院，长沙410083)

摘要：这里系统地介绍了磁张量数据边界识别数值计算的几种方法，包括利用磁张量不变量、水平梯度模法(the total horizontal derivatives，THDR)、解析信号法(The analytic signal amplitude，ASM)、Tilt梯度法、Tilt梯度的水平导数法、Theta图法、Bspan的水平梯度模法等，给出了各种方法的张量组合方式、各自的适用范围及优缺点，利用结果图中的极值点、零点或其他特征点来识别边界。通过对矩形棱柱体的模型验算，证明深度、磁倾角对边界识别影响较大，磁偏角几乎无影响。利用磁梯度不变量、解析信号法、Tilt梯度法得到目标体边界精确、完整，与实际目标体边界吻合度高，表明利用这些方法能够很好地完成磁张量数据的边界识别。

关键词：磁张量； 张量不变量; 磁源边界; 边界提取

0引言

在研究地质目标体的横向不均匀性特别是地质目标体的边缘位置时，磁位场有其独特的优势。这里的地质目标体边缘是指断裂构造线、不同地质体的边界线，实际上是具有一定磁性差异的地质体的边界线。磁力梯度测量作为一种新型的地球物理勘探方法，具有快速、经济、范围大等优点，是划分大地构造单元，进行构造分区，确定断裂构造带的位置，区分不同岩性与地层的分布，进行物性填图快速而有效的手段[1]。磁力梯度张量测量系统的测量对象是磁场矢量分量的梯度，磁测结果能够反映目标体的矢量磁矩信息，可用于描述场源体的磁化方向和几何形态，提高对磁源体的分辨率。随着工艺技术的发展，磁张量测量已经成为现实[2]。现今有关张量数据处理方法的研究受到人们广泛地关注，但大多是针对重力张量数据，而对于磁张量数据的研究方法较少[3]。在地质体的边缘附近，磁梯度是磁场中场变化最剧烈的地方，磁异常变化率较大，它反应了地质体的边界，故所有的边缘识别方法均利用这一特点进行设计[4]。利用磁位场识别地质体边缘的方法分为数理统计，数值计算和其他三大类，这里主要介绍数值计算类[5]，它包括利用磁张量不变量、水平梯度模法、解析信号法、Tilt梯度法、Tilt梯度的水平导数法、Theta图法、BZZ的水平梯度模法等，并设置多个模型来验证各种方法的应用效果与优势。

1边界提取方法

磁法勘探中测量的物理量有地球磁场总场的模量、总磁场模量的空间变化率、地球磁场的三个分量、磁场三分量的空间变化率，即磁梯度张量。

磁梯度张量是磁场矢量的三个分量在相互正交的三个方向的空间变化率，磁场为矢量场，在形式上，梯度张量可以表示为两个三元素矢量的矩阵乘法运算：

(1)

其中:U为磁标势；Bx、By和Bz是磁场矢量B在空间三个方向上的分量。

由磁场强度旋度为零可知，磁梯度张量是对称的，即：

Bxy=Byx,Byz=Bzy,Bxz=Bzx

(2)

而且在无源区，磁势满足拉普拉斯方程：

▽·U=0

(3)

则磁梯度张量对角元素之和为零，即：

Bxx+Byy+Bzz=0

(4)

根据式(2)和(4)可知，磁梯度张量的九个元素中，只有五个元素是独立的，则可将其表示为：

(5)

综上可得磁场三个矢量分量、总场强度以及磁梯度张量各元素在直角坐标系中的关系如图1所示。

地质体边界的圈定一直是磁场数据解释中的重要内容，可以用很多方法对地质体边界进行识别[6]，数值计算类边界识别方法是研究最多、应用最广的边界识别方法。边界识别结果是一种定性或半定量解释结果，与定量解释结果有一定区别，识别结果可作为边界位置定量反演的初值。直接根据原始磁异常不能准确地划分出地质体的边界，但对某个张量数据单独进行处理解释，忽略有用信息，容易造成信号的不合理解释[7]。张量分量的不同组合所产生的不变量形式简单、容易处理解释，并且与磁异常体的大小、形状相关，集中把多个分量的信息增强，能够更好地处理和解释数据[8]。目前常用的磁张量数据边界识别数值计算的方法，包括利用水平梯度模法、解析信号法、Tilt梯度法、Tilt梯度的水平导数法、Theta图法、BZZ的水平梯度模法等，下面研究它们的张量组合方式、各自的适用范围及优缺点。

由实对称矩阵的性质可知，磁梯度张量矩阵具有三个旋转不变量，这三个不变量不受坐标系统旋转变换影响，分别表示为式(6)[8]：

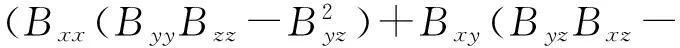
BxyBzz+Bxz(BxyByz-BxzByy))1/3

(6)

这三个张量组合同时包含了五个独立分量，上述磁力张量不变量I1本身具有很好的性质，如不变量等值线图不受地磁场方向影响，能够很好地绘出场源边界，而I2能很好地突出浅部异常体的特征。

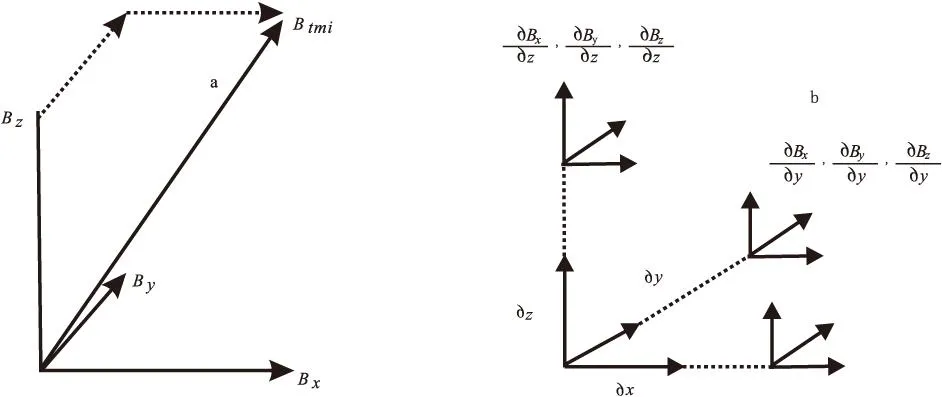
图1　磁场矢量分量、总场强度以及磁梯度张量各元素关系图Fig．1　The relationship diagram of magnetic field vector components, the total field strength and the magnetic gradient tensor elements(a)磁场分量、总场强度；(b)磁梯度张量各元素间关系

水平梯度模也是一种常用的边界识别方法，余钦范[4]指出了可以利用水平梯度极大值法识别磁性体边界，利用重力位与磁位的泊松关系，把磁异常换算为伪重力异常(磁源重力异常)，然后计算伪重力异常水平梯度的模(强度)，经过处理后的水平梯度模便可用来确定物性边界的位置。在水平梯度模极大值位置处绘出标志以表示边界位置，其表达式为式(7)[9]。

(7)

最近几年，国内、外文献有不少关于利用磁异常总梯度模进行磁测资料解释的报导，它能迅速推断磁源的水平边界位置。Roest等[11]人提出了利用三维解析信号法(总梯度模)进行磁异常解释。总梯度模法，又称为解析信号法，其表达式为式(8)[10]：

(8)

解析信号振幅的极大值出现在磁性差异处，利用这些极大值可以确定目标体边界的位置。总梯度模法在磁异常方面研究较多，它受磁化方向影响小，能够准确地识别有一定走向的垂直边界、无限延深厚板等磁性体的位置。吴文贤[10]用模型试验表明了该方法在低纬度地区磁异常分析与解释方面的有效性,并将基于总梯度模的磁异常分析方法应用于老挝爬立山铁矿区的磁测资料处理，由此排除了由化极不稳定导致的虚假磁异常，由该方法确定的磁异常区域与区内磁铁矿体分布位置的吻合性较好,圈定了矿体异常的分布范围，进一步指导矿区铁矿勘探。

Tilt梯度是用垂直梯度比上水平梯度的绝对值的arctan角度(式(9))[11]：

(9)

Hood[15]探讨了应用垂直梯度法和水平梯度法来识别磁性体的垂直边界；Grauch[16]提出用最大水平梯度法探测倾斜台阶的倾斜边界；余钦范[4]利用水平梯度极大值法识别密度和磁性体边界，假定磁源边界为单个垂直边界，磁异常水平梯度模在边界上恰好取得极大值，由此便可确定磁源边界的位置。

Theta图法利用解析信号振幅对总水平导数进行归一化，其θ角的计算公式如式(10)所示[12]：

(10)

式中cosθ的取值在0～1之间，在场源边界处的取值趋近于1。Wijins[14]完成了二度体磁力异常和三度体磁力异常的模型试算以及实际资料处理，指出此法不受磁异常分量和磁化方向的影响，比解析信号振幅的分辨能力更强。

HDT法(horizontaldirectivetendencyordifferentialcurvaturemagnitude)，也可称作水平方向性或是微分曲率幅值[13]，其表达式为式(11)。

(11)

2模型试算

为了检验上述几种边界识别方法的应用效果，现对矩形棱柱体模型引起的磁张量异常进行处理。

模型一：场源空间大小为1 000m×1 000m×500m，场源空间存在一个400m×400m×200m的矩形棱柱体，棱柱体顶部埋深为50m，底部埋深为450m，长方体的水平中心位置为(500m，500m)，磁化强度为1nT/m，x、y方向点距为50 m，测线长度为1 000 m。

当磁倾角为90°，磁偏角为0°时，对于上面提到的6种磁梯度测量边界提取方式分别进行了计算，所得等值线图如图2～图7所示。

图2为磁张量不变量I2的结果等值线图，图2中白色虚线表示实际目标体的边界。可以看出，由磁张量不变量I2等值线图，可以很好地勾绘出实际目标体边界。

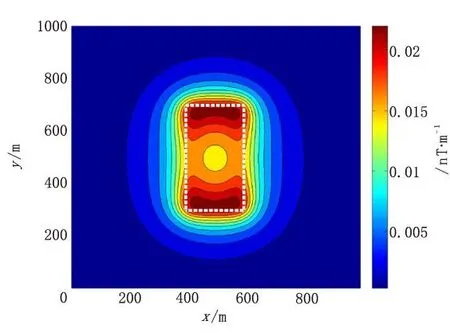
图2　磁张量不变量I2等值线图及边界提取结果Fig．2　Magnetic tensor invariant I2contour 　　　map and boundary recognition results

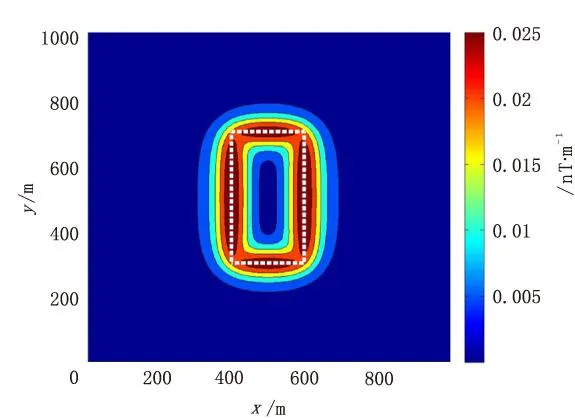
图3　水平梯度模等值线图及边界提取结果Fig．3　Horizontal gradient mode contour map 　　　and boundary recognition results

图3为水平梯度法的等值线图及边界提取结果。其中白色虚线代表实际目标体边界。从图3中可以看出，在水平梯度模的极大值处描绘的标志，与实际目标体边界吻合较好。

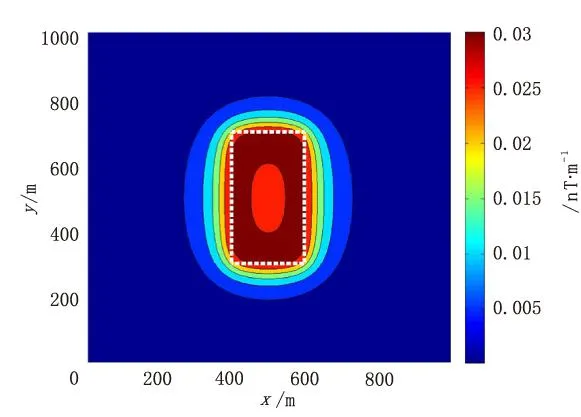
图4　解析信号法的等值线图及边界提取结果Fig．4　Analytical method of signal contour 　　　map and boundary recognition results

图4是利用解析信号法得到的边界提取结果等值线示意图。图4中白色虚线表示实际目标体的边界。对于有一定水平尺度的磁性体，磁异常总梯度模极大值与磁性体浅部边界有较好的对应关系，利用ASM可以较准确地圈定磁性地质体的边界位置。其表达式相对简单，具有较强的分辨迭加异常的特性。从图4中可以看出，利用总梯度模能够很好地确定磁源边界。

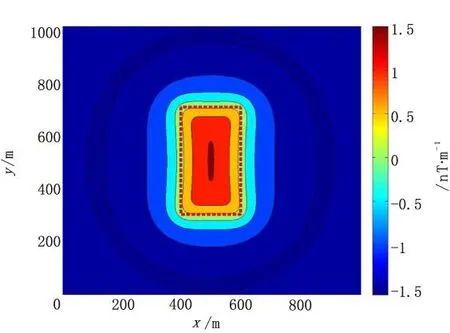
图5　Tilt梯度等值线图及边界提取结果Fig．5　Tilt gradient contour map and 　　　boundary recognition results

图5为Tilt梯度等值线图，图5中红色虚线表示实际目标体的边界。Miller[17]等指出，Tilt梯度在场源上为正值，场源边界处取为零值，在场源外部为负值。Tilt梯度的零等值线位置对应物体源的边界，从图5中可以看出，Tilt梯度的零等值线与目标体的理论边界刚好重合。

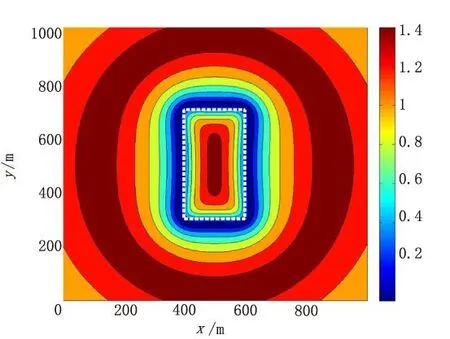
图6　Theta图的等值线图及边界提取结果Fig．6　Theta map contour map and 　　　boundary recognition results

图6显示了利用Theta图计算的等值线图及边界提取结果。其中白色虚线代表实际目标体边界。在cosθ取值趋近于“1”时绘制目标体边界。从图6中可以看出，所得到结果与实际边界吻合度较高。

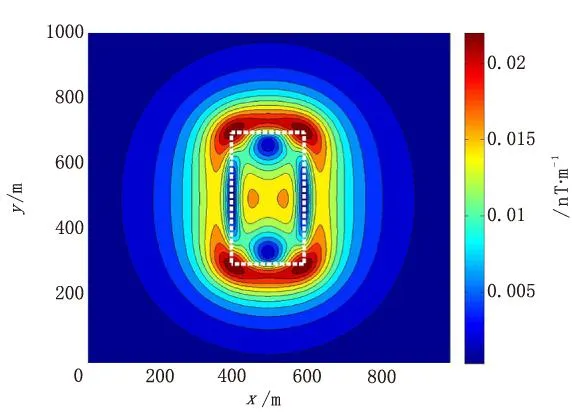
图7　HDT法的等值线图及边界提取结果Fig．7　HDT method contour map and 　　　boundary recognition results

图7显示了HDT法的等值线图及边界提取结果。其中白色虚线代表实际目标体边界。从图7中可以看出，由磁异常的微分曲率幅值的最大值可以确定边界的四个角点，从而确定目标体边界。

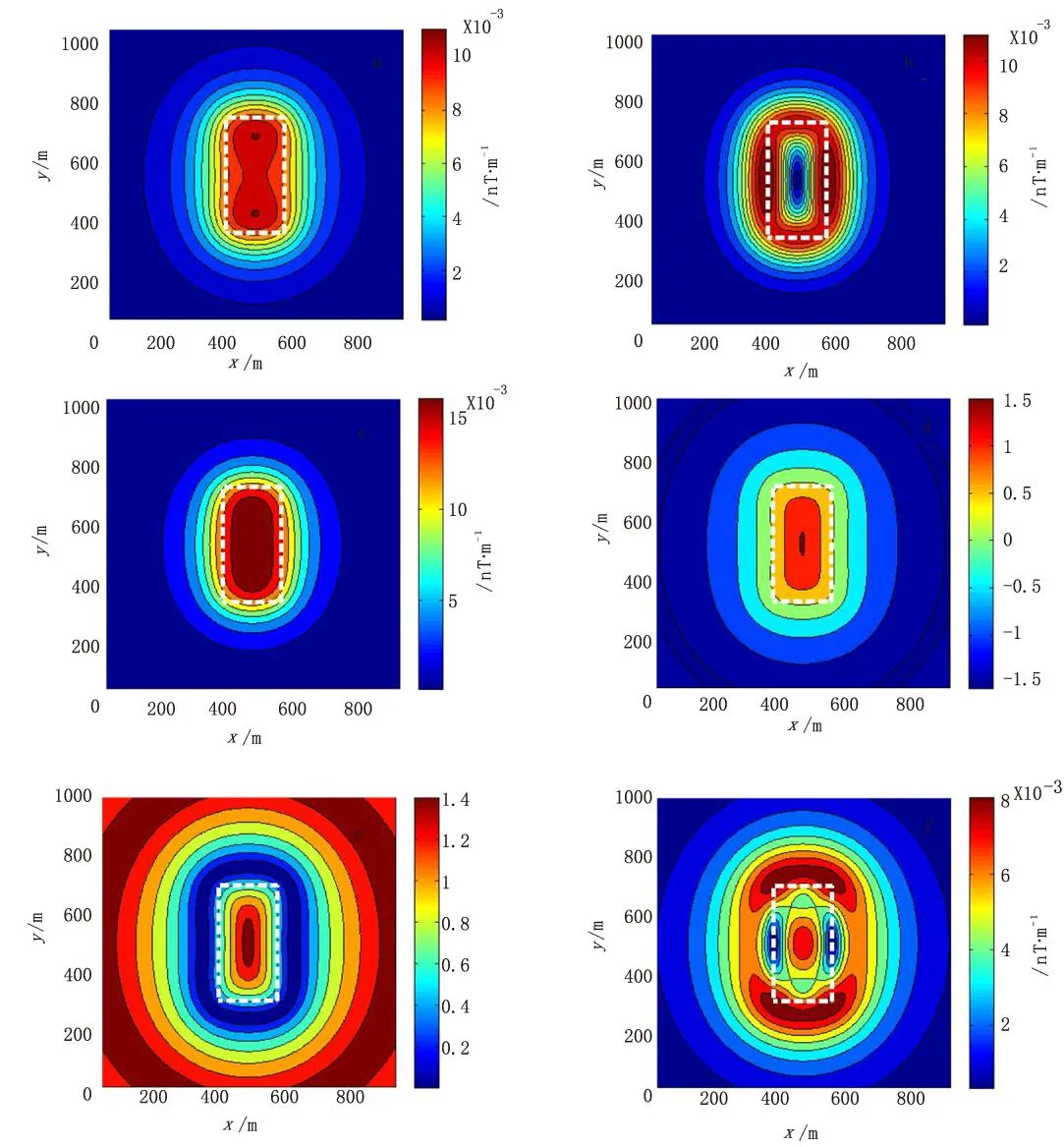
图8　模型二边界提取结果等值线图Fig．8　Edge recognition results based on the model 2(a)磁张量不变量I2; (b)水平梯度模;(c)解析信号法;(d)Tilt梯度;(e)Theta图;(f)HDT法

为验证深度对边界识别效果的影响，现设置模型二：场源空间大小 1 000m×1 000m×500m，场源空间存在一个400m×400m×200m的矩形棱柱体，改变棱柱体顶部埋深为100m，底部埋深为500m，长方体的水平中心位置为(500m，500m)，磁化强度为1nT/m，x、y方向点距为50 m，测线长度为1 000 m。计算结果如图8所示。

从图 8中可以看出识别效果受异常体埋深影响，图9为选用解析信号法提取边界结果随深度变化的误差分布曲线。中心位置深度变化在(50 m，240 m),从图中可看出计算误差在(0，0.2)区间范围内，并且随深度的增加先降后升，即识别能力随着地下目标体埋深的增大先升后降，中心位置深度在(130 m，190 m)区间内可以得到较好的边界识别结果。

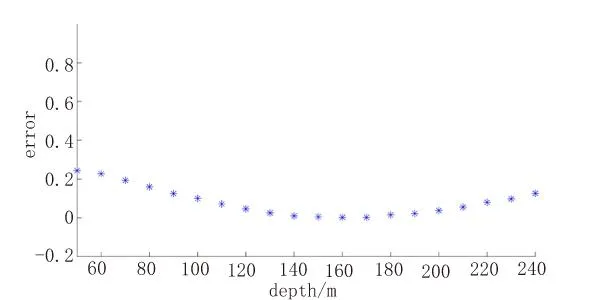
图9　解析信号法提取边界结果随深度变化误差分布曲线Fig．9　The error distribution curves of the results 　　　of analytic signal method vary with depth

为验证不同磁倾角、磁偏角磁异常体边界识别效果，现设置模型三：模型三(A)当磁偏角为45°，磁倾角为90°；模型三(B)当磁偏角为0°，磁倾角为75°。对上述边界识别方法进行计算得到等值线图如图10所示。

由图10、图11中可以看出，改变磁偏角大小，这几种方法的计算结果等值线图几乎没有改变，与实际边界吻合度仍旧较高，说明这几种边界识别方法不受磁偏角的影响；当磁倾角改变时，几种边界提取方法的计算结果与实际目标体的边界有一定的偏差，图12为解析信号法提取边界结果随磁倾角变化误差分布曲线，磁倾角变化范围(0°，90°)，边界识别结果受磁倾角变化的影响较为复杂，误差曲线前半部分呈下降趋势，倾角越大，误差越小，在磁倾角为60°时可取得较为理想的边界识别效果；后半部分随着磁倾角的增大误差先增大后减小。

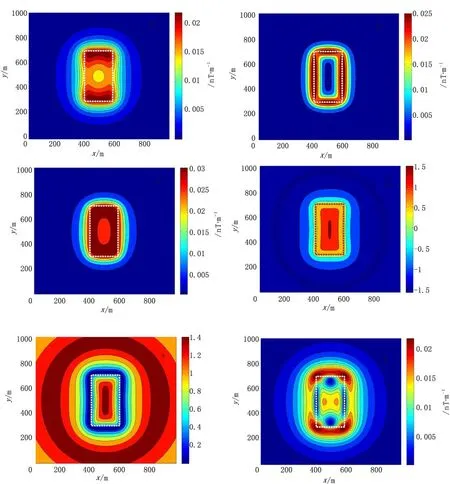
图10　模型三(A)边界提取结果等值线图Fig．10　Edge recognition results based on the model 3(A)(a)磁张量不变量I2；(b)水平梯度模；(c)解析信号法；(d)Tilt梯度；(e)Theta图；(f)HDT法

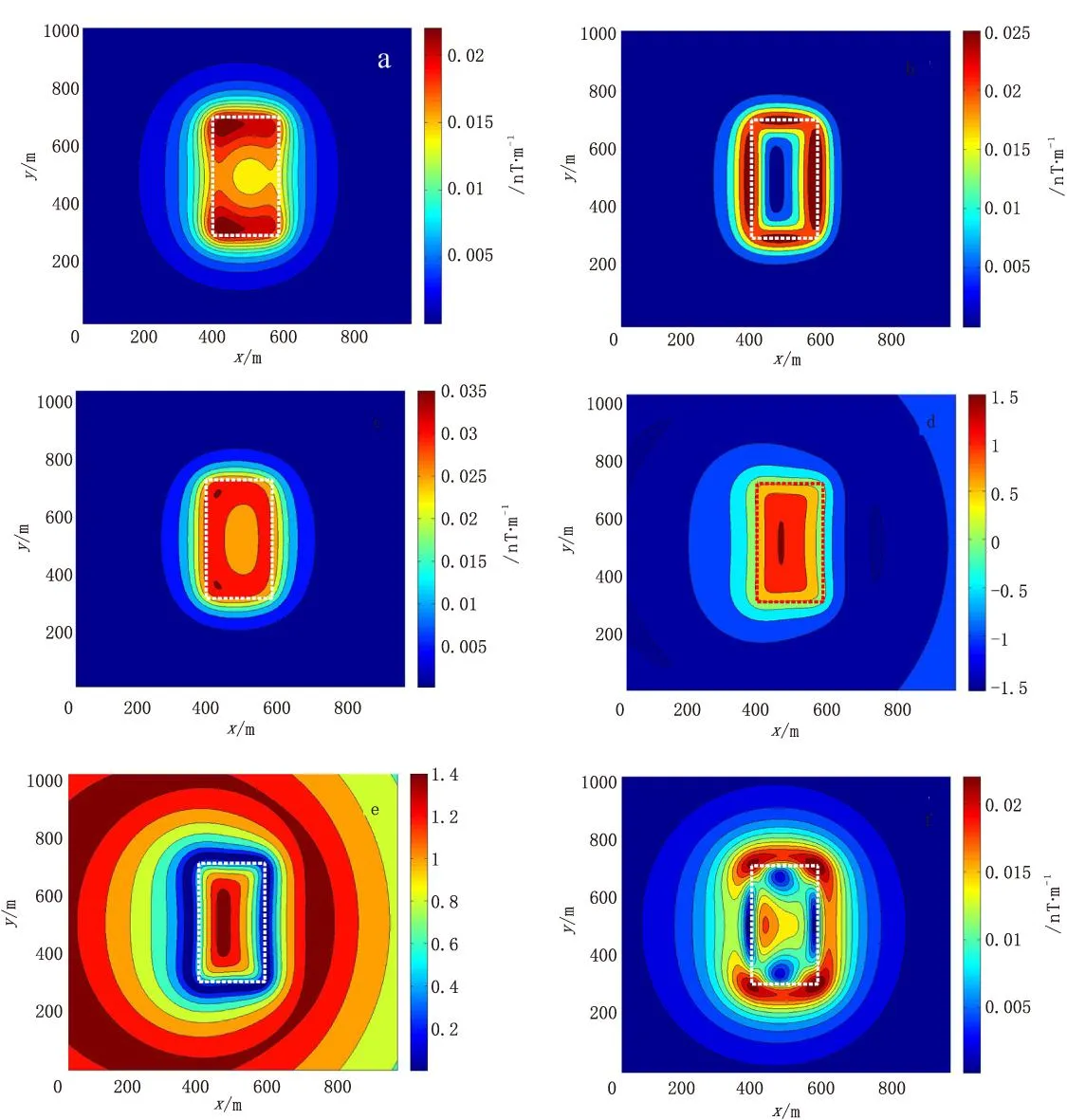
图11　模型三(B)边界识别结果等值线图Fig．11　Edge recognition results based on the model 3(B)(a)磁张量不变量I2；(b)水平梯度模；(c)解析信号法；(d)Tilt梯度；(e)Theta图；(f)HDT法

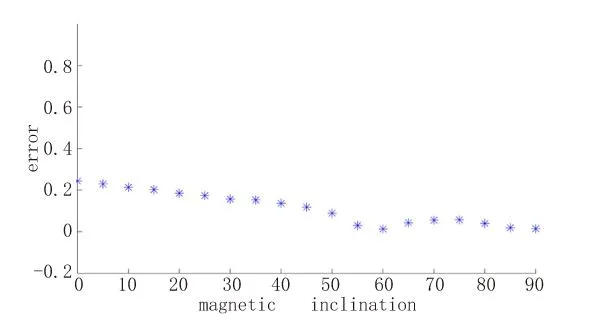
图12　解析信号法提取边界结果随磁倾角　　　　　　　变化误差分布曲线Fig．12　The error distribution curves of the results 　　　of analytic signal method vary with 　　　magnetic inclination

为了验证上述几种边界识别方法在多个地质体模型中的应用效果，现设置模型四(A)：场源空间大小为 1 000 m×1 000 m×500 m，如图所示，场源空间存在两个矩形棱柱体，磁化强度为1 nT/m，左侧棱柱体顶部埋深为50 m，顶部中心位置为(300 m，500 m)，顶部尺寸为400 m×200 m,底部埋深为450 m。右侧棱柱体顶部埋深为50 m，顶部中心位置为(700 m,500 m)，顶部尺寸为400 m×200 m,底部埋深为450 m。x、y方向点距为50 m，测线长度为1 000 m。磁偏角为0°，磁倾角为90°。通过计算所得模型边界提取结果等值线图如图13所示。

模型四(B)：场源空间大小为1 000 m×1 000 m×500 m，场源空间存在三个矩形棱柱体，磁化强度为1 nT/m，左侧棱柱体顶部埋深为50 m，顶部中心位置为(200 m，700 m)，顶部尺寸为300 m×150 m,底部埋深为350 m。中间棱柱体顶部埋深为50 m，顶部中心位置为(500 m，500 m)，顶部尺寸为300 m×150 m,底部埋深为350 m。右侧棱柱体顶部埋深为50 m，顶部中心位置为(800 m,300 m)，顶部尺寸为300 m×150 m,底部埋深为350 m。x、y方向点距为50 m，测线长度为1 000 m。磁偏角为0°，磁倾角为90°。通过计算所得模型边界提取结果等值线图如图14所示。

从图13、图14中可以看出，当出现多个地质体模块时，上述几种数值边界识别方法均可标记出目标体边界，与磁异常体排列顺序无关。其中直接利用磁张量不变量、解析信号、Tilt梯度方法所得结果，与实际边界吻合度更高，能够更好地反映目标体的位置和大小，相比于其他几种方法更为精准。

为了检验上述几种边界识别方法的抗干扰能力,在模型四(B)的基础上加入12%的随机噪声，各边界识别方法计算结果如图15所示。

图15为对上述各个张量组合分别加入12%的随机噪声的边界提取结果，从图15中可以看出在随机噪声使得各等值线图不平滑，这些不平滑影响了异常体边界识别结果。但仍旧可以得到与实际目标磁性体吻合的边界，可看出几种边界识别方法有较好的抗干扰能力。

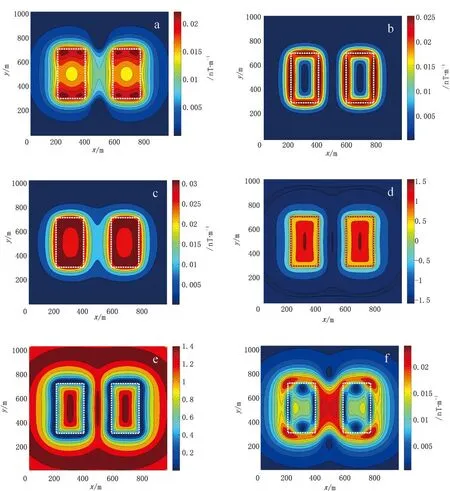
图13　模型四(A)边界识别结果等值线图Fig．13　Edge recognition results based on the model 4(A)(a)磁张量不变量I2；(b)水平梯度模；(c)解析信号法；(d)Tilt梯度；(e)Theta图；(f)HDT法

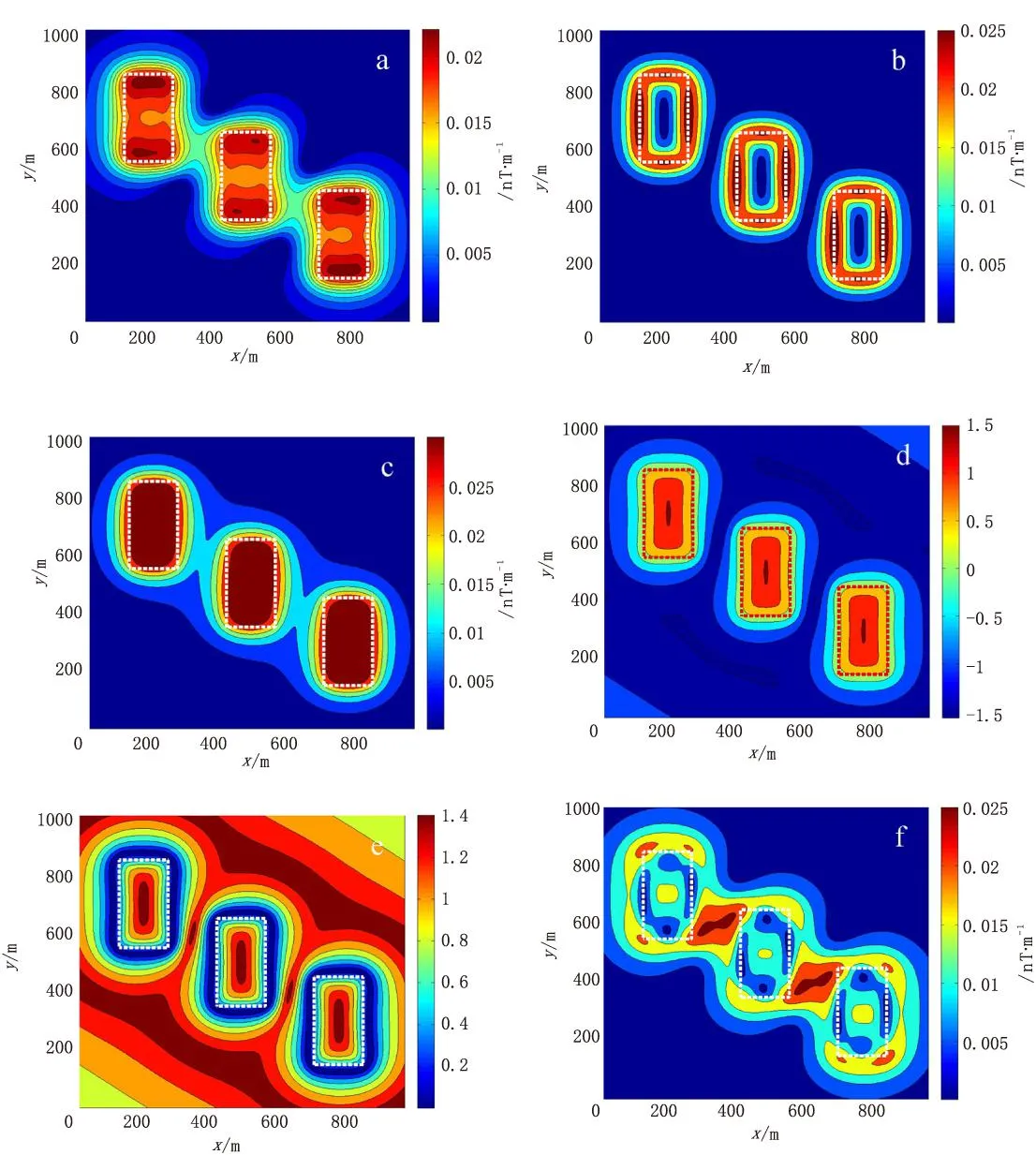
图14　模型四(B)边界识别结果等值线图Fig．14　Edge recognition results based on the model 4(B)(a)磁张量不变量I2；(b)水平梯度模；(c)解析信号法； (d)Tilt梯度；(e)Theta图；(f)HDT法

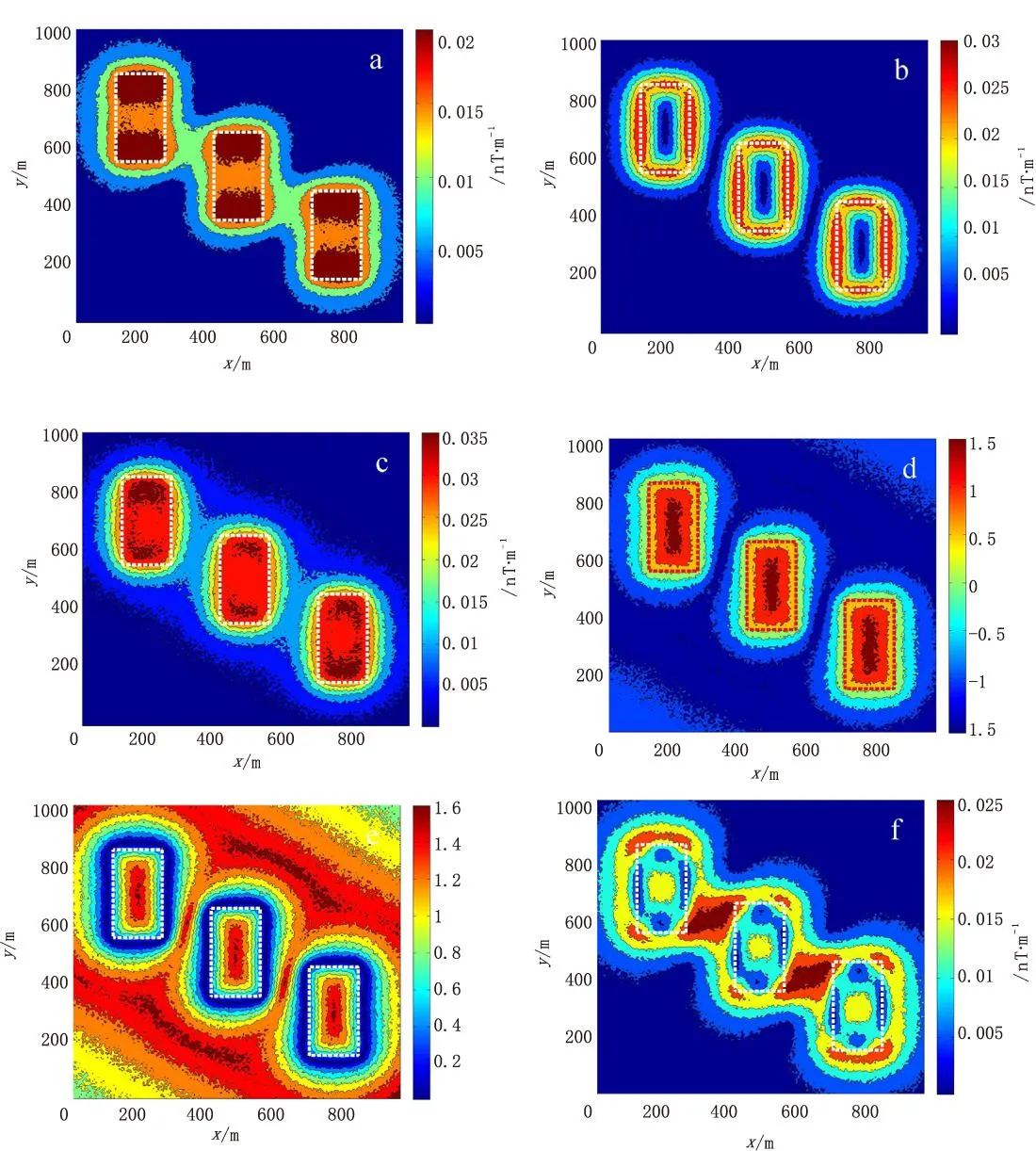
图15　模型四(C)边界识别结果等值线图Fig．15　Edge recognition results based on the model 4(C)(a)磁张量不变量I2；(b)水平梯度模；(c)解析信号法； (d)Tilt梯度；(e)Theta图；(f)HDT法

3结论

作者系统地阐述了磁梯度张量数据边界提取的各种方法，并均进行计算得出结果，针对解析信号法计算出随深度及磁倾角变化的误差分布曲线。识别方法随着地质体埋深的增大而识别能力先上升后下降；在埋深相同的情况下，识别能力不受磁偏角的影响；受磁倾角影响情况较为复杂。通过对矩形棱柱体的结果检验，说明利用磁梯度不变量、解析信号法、Tilt梯度相对于其他边界提取算法所得的边界，能更好地反映磁源的边界位置，特别是对于埋深较浅的垂直棱柱体，其边界与实际模型吻合得非常好。在多个矩形棱柱体模型验算中，几种方法所得边界简单，清晰，易于识别，精确度依旧很高，抗干扰能力较强，证明方法可行。磁梯度张量数据，对于直接勾划异常体的边界、圈定地下异常体具有更高的精度，将其应用于实际磁梯度张量测量时，有一定的指导意义。

参考文献：

[1]马国庆, 李丽丽, 杜晓娟. 磁张量数据的边界识别和解释方法[J]. 石油地球物理勘探, 2012, 47(5): 815-821.

MA G Q, LI L L,DU X J.Boundary detection and interpretation by magnetic gradient tensor data[J]. OGP, 2012, 47(5): 815-821.(In Chinese)

[2]吴招才, 刘天佑. 磁力梯度张量测量及应用[J]. 地质科技情报, 2008, 27(3): 107-110.

WU Z C, LIU T Y. Magnetic gradient tensor: its properties and uses in geophysics[J]. Geological Science and Technology Information, 2008, 27(3): 107-110.(In Chinese)

[3]BEIKI M, PEDERSEN L B, NAZI H. Interpretation of aeromagnetic data using eigenvector analysis of pseudo gravity gradient tensor[J]. Geophysics, 2011, 76(3): L1-L10.

[4]余钦范, 楼海. 水平梯度法提取重磁源边界位置[J]. 物探化探计算技术, 1994, 16(4): 363-367.

YU Q F, LOU H. Locating the boundaries of magnetic or gravity sources using horizon gradient anomalies[J]. Computing Techniques for Geophysical and Geochemical Explosion,1994, 16(4): 363-367.(In Chinese)

[5]王万银, 邱之云, 杨永. 位场边缘识别方法研究进展[J].地球物理学进展, 2010, 25(1): 196-210.

WANG W Y, QIU Z Y, YANG Y. Some advances in the edge recognition of the potential field[J].Progress in Geophysics,2010, 25(1): 196-210.(In Chinese)

[6]BEIKI M, PEDERSEN L B. Eigenvector analysis of gravity gradient tensor to locate geologic bodies[J]. Geophysics, 2010, 75(6): 137-149.

[7]朱自强, 曾思红, 鲁光银. 重力张量数据的目标边缘检测方法探讨[J].石油地球物理勘探, 2011, 46(3): 482-488.

ZHU Z Q, ZENG S H, LU G Y. Discussion on the edge detection technique for gravity gradient tensor data[J]. OGP,2011, 46(3): 482-488.(In Chinese)

[8]AFIF H. SAAD. Understanding gravity gradient statutorily[J]. The Leading Edge,2006, 25(8): 942-947.

[9]PEDERSEN L B, RASMUSSEN T M The gradient tensor of Potential field anomalies: some imp- lications on data collection and data processing of maps [J]. Geophysics, 1990, 55(12): 1558-1566.

[10]吴文贤，范文玉，王永华. 基于总梯度模分析的磁源体边界信息提取及找矿意义[J].地质与勘探,2013,49(6):1164-1169.

WU W X,FAN W Y,WANG Y H.Based on the analysis of total gradient mode of magnetic source body boundary information extraction and prospecting significance[J].Geology and Prospecting,2013,49(6):1164-1169.(In Chinese)

[11]WR ROEST J, VERHOEF, M PILKINGTON, et al. Magnetic interpretation using the 3-D analytic signal [J]. Geophysics, 1992, 57(l): 116-125.

[12]GRAUCH, V.J.S.,CORDELL, LINDRITH.Mapping basement magnetization zones from aeromagnetic data in the San Juan basin,New Mexico[A].//Hinzc W J.The utility of regional and magnetic anomaly[C].Society of Exploration Geophysicists,1985:181- 197.

[13]BRUNO VERDUZEO J, DEREK FAIRHEAD, CHRIS M. GREEN, et al. The meter reader-new in- sights into magnetic derivatives for structural mapping [J]. The Leading Edge, 2004,23(2):116-119.

[14]CHRIS WIJNS, CARLOS PEREZ, PETER KOWALCZYK. Theta map: Edge detection in magnetic data[J]. Geophysies,2005, 70(4): L39-L43.

[15]HOOD P. Aeromagnetic surveying[M].US:Geophysics. Springer US, 1989.

[16]GRAUCH V J S. Limitations of determining density or magnetic boundaries from the horizontal gradient of gravity or pseudogravity data[J]. Geophysics, 1987, 52(1):118-121.

[17]HUGH G MILLER, VIJAY SINGH. Potential field tilt-a new concept for location of potential fied sources[J].Journal of Applied Geophysics, 1994, 32(2-3):213-217.

Discussion of magnetic tensor data target body boundary identification methods

QIN Xiu-ying, LU Guang-yin, ZHU Zi-qiang, CAO Shu-jin

(School of geosciences and info-physics, Central South University, Changsha410083,China)

Abstract:Several methods of the magnetic tensor data boundary identification of numerical calculation are systematically introduced in this paper, including using the magnetic tensor invariant, horizontal gradient modulus method (the total horizontal derivatives, THDR), analytic signal method, the analytic signal amplitude(ASM), Tilt gradient method, the horizontal derivative of Tilt gradient method, Theta map method and the level of the BZZgradient modulus method. Tensor combination of various methods, their respective applicable scope and the advantages and disadvantages are given. Using the results the extreme value point, zero point, or other feature points in the graph to identify boundary. Through the calculation of rectangular prism model, proving that the depth, dip angle has greater influence on the boundary identification, magnetic declination almost had no effect. The geological edges by using the method of magnetic gradient in-variants, analytic signal and Tilt gradient method are accurate and complete. The result is in accordance with model edge. Showing that is able to complete the boundary identification of the magnetic tensor data.

Key words:magnetic tensor; tensor invariant; magnetic source boundary; boundary extraction

中图分类号：P 631.2

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.01.03

文章编号：1001-1749(2016)01-0019-11

作者简介：秦秀颖(1989-)，女,硕士,主要从事重磁数据处理与解释方面的研究,E-mail:iwanted@126.com。

基金项目:国家自然科学基金(41174061,41374120)

收稿日期：2015-01-04改回日期：2015-04-01