电动汽车电池箱结构随机振动疲劳分析

王文伟++程雨婷++姜卫远++刘志山

摘 要：电动汽车电池箱的结构设计应该满足多变运行环境和工况下的疲劳寿命要求。通过有限元软件对某款电动汽车电池箱结构进行建模，基于频域法分析其在随机振动环境下的响应，根据Miner提出的线性疲劳累计损伤理论和材料S-N曲线，对随机振动条件下的电池箱结构进行疲劳分析。结果表明，原结构可以满足随机振动试验要求。为随机振动环境下电池箱结构的疲劳分析提供了一种有效的计算方法。

关键词：随机振动；疲劳分析；有限元分析；电池箱；电动汽车

中图分类号：U469.72文献标文献标识码：A文献标DOI：10.3969/j.issn.2095-1469.2016.01.02

Abstract：The design of electric vehicle（EV） battery boxes should meet fatigue life requirements under changeable operating conditions. A finite element model was built for the EV battery box， and the response to random vibration was analyzed based on frequency domain methods. The Miner's linear fatigue damage accumulation rule and the S-N curve of the materials were used to analyze the fatigue life of battery box， and the result shows that the original structure can meet the requirements of random vibration test. An effective calculation method is proposed for random vibration fatigue analysis of battery box structure.

Keywords：random vibration； fatigue analysis； finite element analysis； battery box； electric vehicle

由于路面的不平度，电动汽车在行驶过程中所承受的载荷是随机的，电池箱是电动汽车能量供给的关键设备，作为电池组的载体，对电池组的安全工作和防护起着关键的作用，影响整车的安全性。因此电池箱结构设计应满足多变运行环境和行驶工况下的疲劳寿命要求。

随机振动下结构疲劳分析方法主要有时域和频域两种方法，时域法中经典的雨流循环计数方法被认为是最准确的方法，但计算量较大，在工程实践中应用受到很大限制[1]。因此，当前主要使用频域的谱分析法，通过功率谱密度（Power Spectrum Density，PSD）从频域角度准确地描述载荷的统计规律。此外，目前对电池箱的疲劳分析大多在设计完成后按照相关要求，使用随机振动台进行试验，效率低成本高。随着计算机技术及仿真技术的不断发展，使用高性能计算机及相应的软件平台便能实现设备随机振动仿真分析。但对于电池箱结构，随机振动疲劳仿真分析非常少，且对于频域法的应用也尚未形成一套高效可靠的方法。

本文采用有限元方法并基于频域法，根据Miner提出的线性累积损伤理论和材料S-N曲线，对随机振动试验的电池箱结构疲劳寿命进行分析，为随机振动环境下电池箱结构的随机振动分析和疲劳设计提供了一种有效的计算方法。

1 随机振动分析

随机振动是指未来任一给定时刻的瞬时值不能预先确定的机械振动，无法用确定性函数而须用概率统计方法定量描述其运动规律的振动。随机振动条件下结构的疲劳分析方法有很多种，主要分为时域和频域两种分析方法，由于频域内的主要优点是能够描述振动频率，了解振动中的有效频率分量，因此对随机振动的应力分析，主要使用频域的谱分析法。在频域中， PSD是一个最基本的量，通过谱分析可以了解随机振动的频率成分[2]。

功率谱密度的表达式为：

式中：为平稳随机振动的自相关函数；为圆频率。

2 Miner线性累积损伤理论

疲劳累积损伤理论的研究已经持续了数十年，已有疲劳累积损伤理论大致可分为确定性的模型和基于可靠性设计发展起来的概率性模型。确定性模型又可以分为线性累积损伤理论和非线性累积损伤理论。虽然模型众多，但Miner线性累积损伤理论由于其形式简单，使用方便，且在多数情况下其寿命估算与试验结果有相当程度的吻合，成为目前应用最为普遍的疲劳寿命预测方法[3]。

工程界计算结构随机振动疲劳寿命比较简单并且容易进行的是Steinberg提出的应力服从高斯分布的三区间法[4]。Steinberg将Von Mises应力处理成三个阶段，如图1所示，以第一主应力1，第二主应力2，第三主应力3为边界来进行定义。如表1所示，在应力区间-1～1、-2～2、-3～

3 发生振动的时间分别为总时间的68.3%、27.1%和4.33%，认为大于3的应力仅发生在0.27%的时间内，不对结构造成损伤[5]。

Miner根据材料吸收净功原理，提出了随机载荷下的疲劳线性累计损伤计算公式[6]：

式中：Ni为应力幅值为i时，构件破坏的平均激励周期数；ni为强度为i时实际激励周期数；D为按任意次序受到强度为i的激励ni（i=1， 2， …， r）次的总损伤度。

当疲劳损伤值D小于1时，结构在要求的时间内不会发生破坏，满足疲劳破坏要求，且D越小，结构破坏的时间越长；D值累计到1，结构不能满足疲劳破坏要求，在要求时间内会发生破坏。

3 电池箱结构随机振动疲劳分析

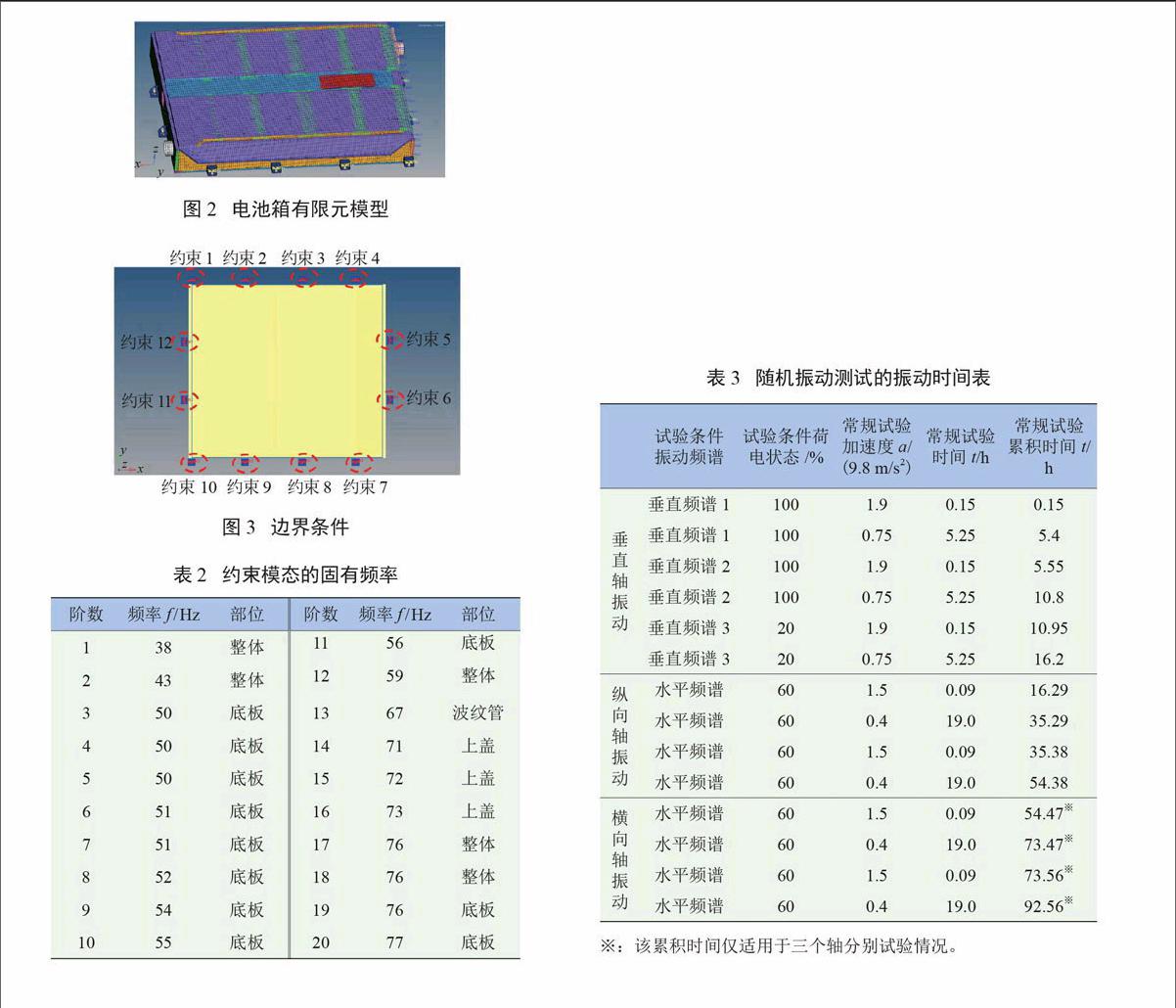
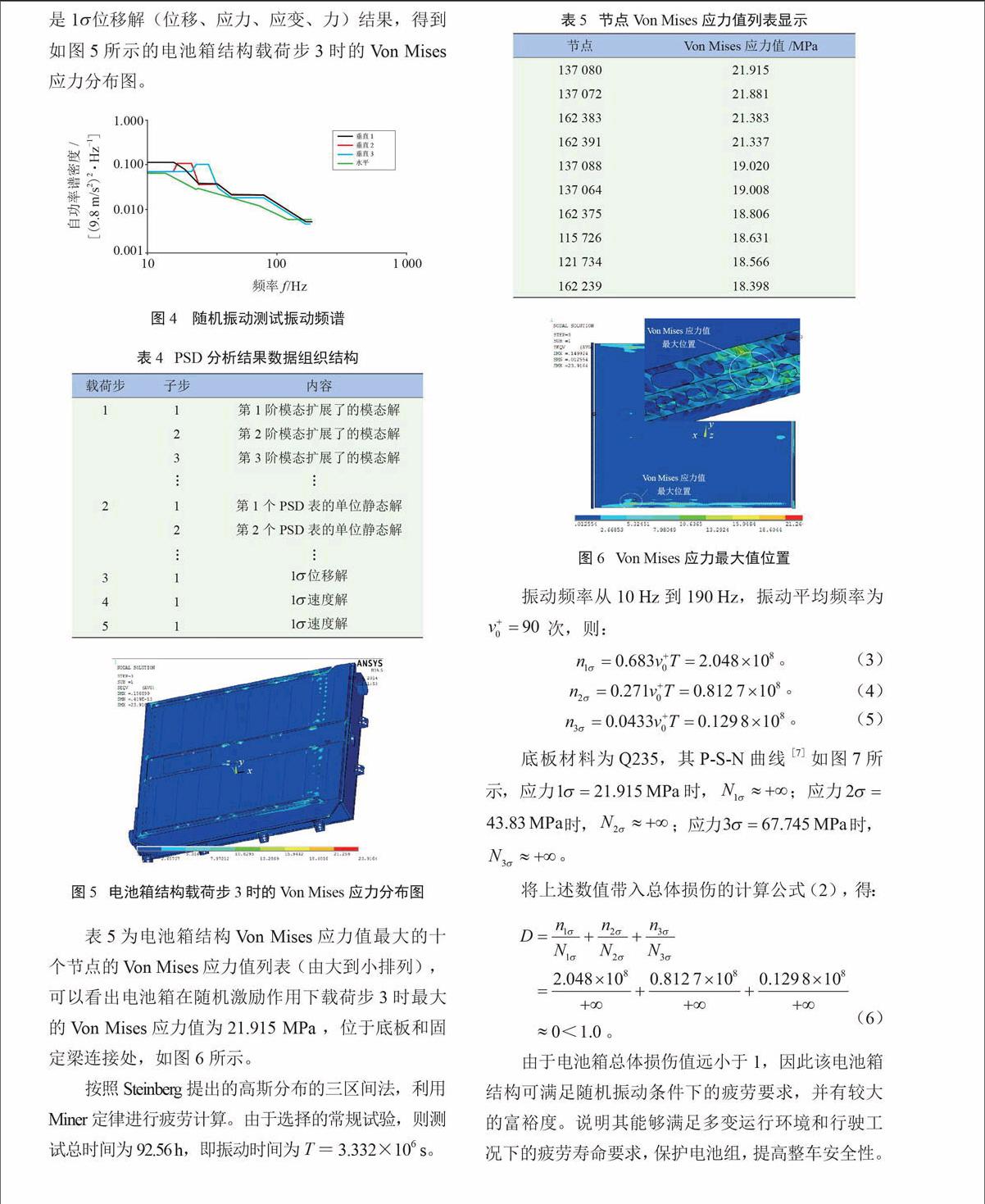
应用Hypermesh软件建立电池箱结构的有限元模型，如图2所示，共117 837个单元。电池箱结构主要采用壳单元，根据分析目的不同，单元分别采用7 mm和12 mm两种尺寸；电池连接杆采用beam单元模拟，并与电池、电池夹板固连；焊点采用Rbe2和Cweld两种连接方式进行模拟，对于电池，作为质量点进行模拟。对电池箱模型进行约束模态分析，边界条件如图3所示，约束模态是施加约束之后的模态分析，能够反映结构的真实振动情况。分析得到约束模态的固有频率见表2，一阶频率结果为38 Hz。分析结果与实际振动情况基本相符，说明模型具有一定的准确性，可以用于随机振动疲劳分析。

SAE J2380是电动汽车电池的振动测试标准，是为了确保电动汽车电池在长时间、道路载荷引起的振动条件下的性能和寿命而制定的标准。振动测试适用于纯电动汽车或混合动力电动汽车，为电池在随机振动条件下的性能和寿命测试提供一种测试程序，包括试验设备、试验条件以及试验步骤等，其中，作为激励的振动频谱是基于不平道路测量而得到的。电池箱是电池的载体，在承受与电池同样运行工况载荷下应该具有一定的疲劳寿命，保证电池的安全，因此，本文基于SAE J2380标准，选择其测试程序中随机振动测试振动频谱作为激励，对电池箱结构进行疲劳分析。

如表3所示，选择常规试验加速度值，同时确定了电池箱的x、y、z各轴要求的振动时间和总振动时间，对应的加速度PSD如图4所示，其中“垂直1”、“垂直2”、“垂直3”分别对应表3中垂直频谱1、2、3，“水平”对应表3中水平频谱。

将模型导入ANSYS软件，输入如图4所示的随机振动激励，对电池箱进行随机振动分析，计算完成后进行结果后处理。表4为ANSYS软件PSD分析结果的数据组织结构，其中提取载荷步3也就是1位移解（位移、应力、应变、力）结果，得到如图5所示的电池箱结构载荷步3时的Von Mises应力分布图。

表5为电池箱结构Von Mises应力值最大的十个节点的Von Mises应力值列表（由大到小排列），可以看出电池箱在随机激励作用下载荷步3时最大的Von Mises应力值为21.915 MPa ，位于底板和固定梁连接处，如图6所示。

按照Steinberg提出的高斯分布的三区间法，利用Miner定律进行疲劳计算。由于选择的常规试验，则测试总时间为92.56 h，即振动时间为T=3.332×106 s。

振动频率从10 Hz到190 Hz，振动平均频率为 次，则：

底板材料为Q235，其P-S-N曲线[7]如图7所示，应力时，；应力

时，；应力时，。

将上述数值带入总体损伤的计算公式（2），得：

由于电池箱总体损伤值远小于1，因此该电池箱结构可满足随机振动条件下的疲劳要求，并有较大的富裕度。说明其能够满足多变运行环境和行驶工况下的疲劳寿命要求，保护电池组，提高整车安全性。

4 结论

应用有限元分析软件分析某款电动汽车电池箱结构在随机振动环境下的响应，并基于频域法利用Miner提出的线性疲劳累计损伤理论和材料S-N曲线，对随机振动试验的电池箱结构的疲劳寿命进行了分析，并发现结构中首先发生损伤的位置。为随机路面激励下的电动汽车电池箱结构的随机振动分析和疲劳寿命估算提供了一种有效的计算方法，对实际生产有工程指导意义。

参考文献（References）：

刘龙涛，李传日，程祺，等. 某结构件的随机振动疲劳分析[J].振动与冲击，2013，32（21）：97-101.

Liu Longtao，Li Chuanri，Cheng Qi，et al. Random Vibration Fatigue Analysis for a Structure [J]. Journal of Vibration and Shock，2013，32（21）：97-101.（in Chinese）

瞿云飞. 垃圾车车厢随机振动疲劳分析及结构优化 [D].南京：东南大学，2008.

Qu Yunfei. Random Vibration Fatigue Analysis and Structure Optimization of Garbage Truck's Compartment [D]. Nanjing：Southeast University，2008.（in Chinese）

惠纪庄，孙德仕，邹亚科. Miner线性累计损伤理论在汽车试验场可靠性试验强化系数研究中的应用 [J]. 工程设计学报，2008，15（4）：264-267.

Hui Jizhuang，Sun Deshi，Zou Yake. Application of Miner Linear Cumulative Damage Law in Reliability Test Intensifying Coefficient on Automotive Proving Ground [J]. Journal of Engineering Design，2008，15（4）：264-267. （in Chinese）

庄表中，陈乃立. 随机振动的理论及实例分析 [M]. 北京：地震出版社，1985：216-222.

Zhuang Biaozhong，Chen Naili. Random Vibration Theory and Case Study [M]. Beijing：Seismological Press， 1985：216-222.（in Chinese）

李舜. 机械疲劳与可靠性设计 [M]. 北京：科学出版社，2006：22-28.

Li Shun. Mechanical Fatigue and Reliability Design [M]. Beijing：Science Press，2006：22-28.（in Chinese）

姚卫星. 结构疲劳寿命分析 [M]. 北京： 国防工业出版社，2003： 82-86.

Yao Weixing. Fatigue Life Prediction of Structures [M]. Beijing： National Defence Industry Press，2003：82-86.

（in Chinese）

鲁惠民，陈远远. 机械工程材料性能数据手册 [M]. 北京：机械工业出版社，1994.

Lu Huimin，Chen Yuanyuan. Mechanical Engineering Material Performance Data Manual [M]. Beijing：China Machine Press，1994.（in Chinese）

Li Junqiu，Tian Helei，Wu Puen. Analysis of Random Vibration of Power Battery Box in Electric Vehicles [C]. ITEC Asia-Pacific，2014.

LEE Y L，PAN J，HATHAWAY R，et al. Fatigue Testing and Analysis （Theory and Practice）[M]. London：ELSEVIER，2005：126-132.

SAE J2380-2009.Vibration Testing of Electric Vehicle Batteries [S]. USA：Society of Automotive Engineers，2009.