网式过滤器的计算模型选择及内部流场分析

陶洪飞，朱玲玲，马英杰，滕晓静，郑文强

(新疆农业大学水利与土木工程学院，乌鲁木齐 830052)

2010年中央1号文件《关于加快水利改革发展的决定》提出加大水利建设，实施最严格的水资源管理制度，在新疆农业用水占社会经济总用水的96%，而对GDP的贡献率却只有17.1%，而农业灌溉仅有39.2%采用了高效节水灌溉，对于水资源短缺的新疆来说农业节水潜力还很大[1]。根据《新疆高效节水建设方案》及《新疆农业节水建设发展规划》确定了每年完成农业高效节水面积20万hm2以上，至2020年新疆农业高效节水面积累计达到286.667万hm2以上的推广目标。目前，新疆已建的有关农业高效节水工程，灌溉水源绝大部分为地下水，但许多地区的地下水超采严重，所以未来选择地表水作为灌溉水源已成为新建微灌工程的最优选择[2]。新疆河水多为山溪性河流，泥沙含量高，易造成灌水器(如滴头、微喷头等)堵塞，目前，采用的是沉沙池和组合式过滤器的方法去除微灌用水中的泥沙，以防止灌水器堵塞，从而保障工程的正常运行[3,4]。过滤器是微灌系统中的关键性设备之一，其中网式过滤器相对于砂石过滤器和叠片过滤器而言，具有容易操作、更方便清洗及对无机污染物有较高的去除效率等优势[5]。目前，大部分学者[6-11]开展了有关网式过滤器系列产品的水力性能、去除效率及结构优化等方面的研究。WU[12]根据网式过滤器的结构参数和大量的水头损失试验数据，得到了一个水头损失计算的三维模型。

通过查阅相关文献，发现对网式过滤器内部流场的研究很少，分析原因是网式过滤器的内部结构较为复杂，很难通过现有的测试手段(如PIV或LDP)来测量速度场，但随着计算机的广泛应用以及计算机容量的增大，仿真模拟流动已具有很高的可靠性和准确度。故选择正确的数学模型对网式过滤器中的流场进行数值模拟不失为一种有效的方法。因此，笔者采用Fluent软件开展了网式过滤器过滤过程中的清水流场模拟，并将计算结果同物理试验结果对比，从而选择最适合模拟网式过滤器内部流场的数学模型，并在此基础上分析了该过滤器的清水流场，计算结果为该过滤器的后续研究工作奠定了基础，同时也为研究网式过滤器提供了一种新的研究手段。

1 网式过滤器的介绍

由图1可知，网式过滤器由罐体、滤网、控制器等主要部分组成，其关键参数包括罐体长度1.031 m，直径0.254 m；滤网长度0.961 m，直径为0.2 m；进、出口直径均为0.2 m；排污口直径0.05 m。

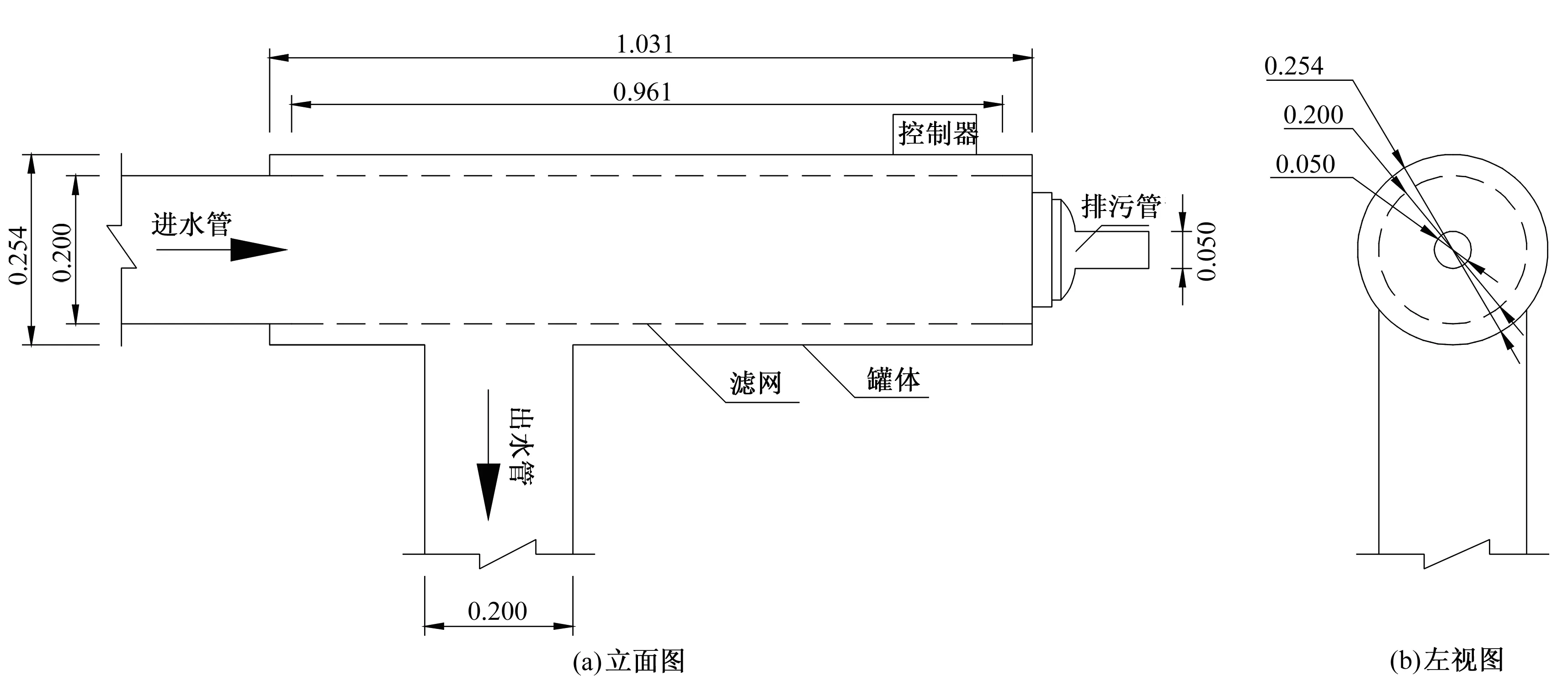
图1 网式过滤器结构示意图(单位：m)Fig.1 Structural diagram of screen filter

过滤器的工作原理描述如下：当灌溉水从进水管流入网式过滤器中，所有大于网孔孔径尺寸的污物都会滞留在滤网上，而过滤水则流向出水管；随着污物的累积，水头损失逐渐增大，当水头损失达到预设压差值时，控制器自动开启排污阀进行排污，排污的同时过滤依然进行，满足灌溉需水要求，当达到预设的排污时间时，排污阀自动关闭，冲洗结束，继续过滤。

2 网式过滤器的CFD模拟

2.1 数学模型

采用Fluent软件中的多孔介质阶跃(Porous Jump)模型来模拟滤网，多孔介质相关参数表达式如下：

(3)

式中：C1为阻力系数，m-2；C2为惯性损失系数，m-1；α为渗透率，m2；D为滤网孔直径，mm；ε为孔隙比(也叫“筛分面积百分比”)，%。

根据物理试验中采用的滤网参数：滤网孔直径D=0.18 mm，孔隙比ε=38%，丝径d=0.112 mm。根据给定的参数值，可计算得到：C1=3.24×1010m-2，C2=219 703.2 m-1，α=3.09×10-11m2。数值计算时考虑过滤网的厚度，其值为0.001 m。

分别选用Fluent6.3提供的Standardk-ε、RNGk-ε及Realizablek-ε为数值计算的湍流模型，与多孔介质阶跃模型耦合求解。这3种模型的湍动能k和耗散率ε的方程见文献[13]。

2.2 坐标建立

图2为网式过滤器的三维坐标。从图2中可知该过滤器的长度方向为X坐标，宽度方向为Z坐标，高度方向为Y坐标。为分析该网式过滤器中的流场分布情况，分别截取X=0.51 m、Y=0 m及Z=0 m 3个典型代表面进行分析研究。并定义远离出水口一侧的滤网为上滤网，靠近出水口一侧的滤网为下滤网；分别选取Y=±0.114、±0.1、±0.086断面与Z=0断面相交的6条线：Y1=0.114(上滤网外侧)、Y2=0.1(上滤网)、Y3=0.086(上滤网内侧)、Y4=-0.086(下滤网内侧)、Y5=-0.1(下滤网)、Y6=-0.114(下滤网外侧)来分析滤网及其内、外侧的流速。

图2 三维坐标Fig.2 Three-dimensional coordinate

2.3 网格划分及计算方法

为减少数值模拟的计算工作量和保证计算精度，对过滤器的计算网格进行了优化。将过滤器的网格进行分块划分，进、出口因为结构简单，采用六面体结构性网格，其余部分采用四面体非结构网格，网格总数为123 252个。

对网式过滤器的数值计算采用非定常的压力基隐式算法，研究的计算区域和控制方程的离散均采用有限体积法。采用Fluent6.3提供的SIMPLE算法来计算压力与速度的耦合方程，差分格式采用精度更高的二阶迎风格式。残差标准为1.0×10-3，迭代时间步长为0.000 1 s。

2.4 边界条件

(1)过滤器进水管中运动的水流，可近似视为均匀流，取进流方向与X轴正向一致，故设置进水口的边界条件为速度进口：U=u，V=0，W=0。根据网式过滤器物理模型试验情况，进流量为352.1 m3/h，则根据流速定义可得该工况下u= 3.11 m/s。

(2)网式过滤器出水口的边界条件设置成压力出口，压力大小为200 kPa。

(3)网式过滤器的罐体、管道内壁及排污管均按固壁定律进行处理，采用无滑移边界条件，即U=V=W=0。

3 最优数学模型的确定

3.1 水头损失对比

对于过滤器而言，我们最为关注的是其水头损失，因为其值的大小是评价过滤器性能的一个重要标准。表1为物理试验结果与数值模拟结果的水头损失对比情况，从表1中可知，物理试验中网式过滤器的水头损失为3 m，而紊流模型中的Standardk-ε模型、RNGk-ε模型、Realizablek-ε模型的计算水头损失分别为3.91、3.18、3.12 m，与物理试验结果的相对误差分别为30.3%、6.0%、4.0%，因此，Realizablek-ε模型与多孔介质阶跃模型耦合的计算结果同物理试验结果吻合最好。同时也验证了Realizablek-ε模型可以模拟高应变率及弯曲程度较大的流动[14,15]。

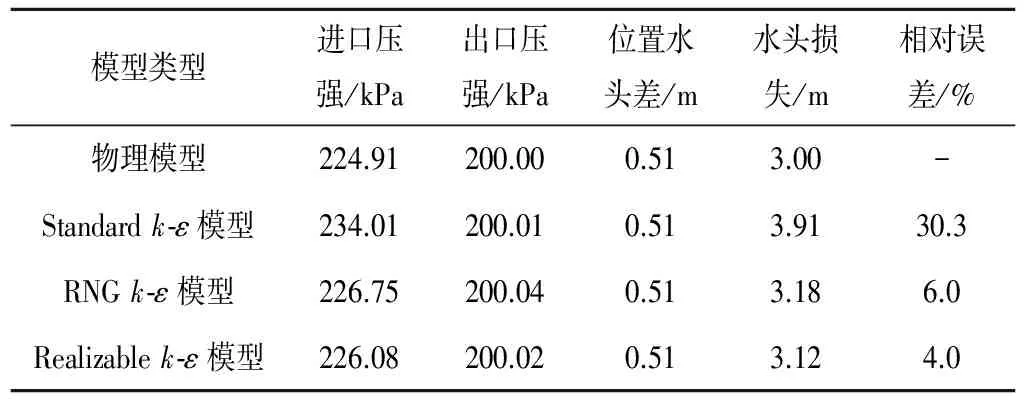
表1 结果对比Tab.1 Results comparison

3.2 计算耗时对比

网式过滤器的数值计算是在同一台计算机上进行，计算机内存都占用127 MB，CPU都占用25%，而当进、出口流量平衡，即完全收敛时，从表2可知，RNGk-ε模型计算用时272 min> Standardk-ε模型计算用时271 min> Realizablek-ε模型计算用时269 mim，但总的来说，三者计算时间相差不大，最长与最短的计算相差仅为3 min。

表2 3种模型的计算时间对比Tab.2 Time comparison of three models

通过水头损失和计算耗时对比，最终选择Realizablek-ε模型与多孔介质阶跃模型来模拟网式过滤中的流场。

4 流场分析与讨论

4.1 速度场对比

图3为网式过滤器中不同断面的速度矢量分布图。从图3(b)和图3(c)中可知，水流从进水管处均匀地流入网式过滤器中，当水流进入罐体时，水流的速度分布特性发生改变，一部分水流进入上滤网，通过滤网孔进行过滤；一部分水流进入下滤网进行过滤，当突然遇到出水口边界时，流速分布发生了巨大的变化，水流由沿X轴正向运动快速转变为沿出水管右侧斜向下运动，从而造成出水管左侧的部分区域产生漩涡，水流运行33 cm左右的距离后，水流沿出水管均匀地向下运动；而X=0.61 m处以后的水流速度大部分呈“点状”分布，说明流速很小。从图3(a)中可知水流在出水管中的流速是关于Z=0截面对称分布的，靠近管壁内侧的水流流速较大，在运动至距出水口10 cm处时，水流流速会减小。

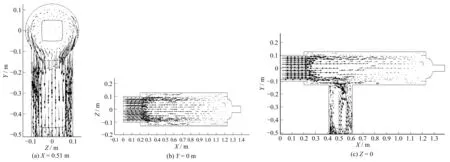
图3 不同断面的速度矢量图Fig.3 Velocity vector diagram of the different section

图4为网式过滤器中不同断面的速度云图。从图4(b)和图4(c)中可以看出进水管中的水流流速分布比较均匀，为3.0 m/s左右；当水流运动至罐体时，过水断面面积增大，水流流速减小，水流继续运动一段路程，过水断面面积没变，但流速却沿X方向逐渐减小，最终达到一个恒定值为0.5 m/s左右。这是因为受到排污口固体边界条件的影响，当水流运动至该处时，水流会发生反向流动，与沿X轴正向运动的水流发生碰撞、摩擦和混掺，从而消耗大量的能量，造成水流流速减小。由于出水口边界条件影响，出水口中间处的水流流速依然较大，为5.0 m/s左右，而左、右侧漩涡处的流速较小，为0.5 m/s左右。从图4(a)可知出水管中的水流流速关于Z=0断面对称分布，水流在出水管Y=-0.12 m左右时的流速最大，5.0 m/s左右。

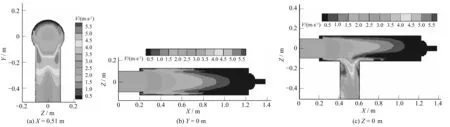
图4 不同断面的速度云图Fig.4 Velocity contours diagram of the different section

4.2 压强场对比

图5为网式过滤器中不同断面的压强场。从图5(a)可知出水口正上方罐体中的水流压强由中心向四周逐渐减小，与速度流场分布规律相反，中心处压强最大，可达230 kPa左右，滤网附近最小的压强为210 kPa左右，两者相差约20 kPa。从图5(b)可知，X=0～0.2 m处，压强分布比较均匀，X=0.2～0.75 m处，上、下滤网的内外压差较大，这是因为水流进入罐体后会以一个相对较大的流速分别流向上、下滤网，并经过滤网孔完成过滤，从而造成滤网的内外压差；X>0.75 m，上、下滤网的内外压差较小，压强分布较均匀。从图5(c)可知进水管处的水流压强明显大于出水管处的水流压强。由于受到罐体中上、下滤网及出水口边界条件的影响，水流从进水管流至出水管过程中会发生局部水头损失和沿程水头损失。故当位置水头和流速水头一定时，进水管处的压强大于出水管处的水流压强，与实际液体恒定总流的能量方程相符合。

图5 不同断面的压强场Fig.5 Pressure flow of the different section

5 流速讨论

图6为水流流速沿X轴的变化曲线。从图6(a)中可得出2点：①上滤网及上滤网外侧的水流流速沿X轴的变化包含两个阶段：流速迅速增大阶段。X=0.2～0.25 m时，上滤网及上滤网外侧的水流流速沿X轴迅速增加，但上滤网的水流流速增加幅度明显大于上滤网外侧，上滤网的流速最大值达2.2 m/s左右，约为上滤网外侧流速最大值的两倍。流速逐渐减小阶段。X=0.25～1.23 m时，上滤网及上滤网外侧的水流流速逐渐减小，虽然减小幅度不同，但减小趋势大体相同。②上侧滤网内侧的水流流速沿着X轴逐渐减小，且水流流速比上滤网外侧的水流流速大很多，但两者的流速差却沿着X轴逐渐减小，两者的最大流速差约为2 m/s；当X=1.05～1.191 m时，上滤网内、外侧的水流流速大体相同，流速差几乎为0。从图6(b)中可知，下滤网及其内外侧的水流流速沿X轴方向的变化规律，与上滤网及其内外侧的有所不同，主要是因为出水口边界条件的影响。

图6 水流流速沿X轴的变化曲线Fig.6 Change curve of water velocity along X axis

综上所述，滤网内、外侧的水流流速沿X轴方向的分布很不均匀，从而影响网式过滤器的过滤效率，特别是网式过滤器尾部附近的滤网，内、外侧流速相差较小，水的渗透率就较小，导致过滤效率较低，如何提高网式过滤器的过滤效率值得进一步研究，可通过改变出水管出水口位置解决水流流速分布不均匀的问题。

6 结 语

利用Fluent6.3软件对网式过滤器的内部流场进行数值模拟，主要得到以下结论。

(1)Realizablek-ε模型与多孔介质阶跃模型能更好地模拟该网式过滤器的内部流场，这为今后该过滤器的结构优化、冲洗过程及水沙两相流流场的数值模拟奠定了基础。

(2)得到了水流从进水管进入网式过滤器并流出出水管的运动状态，指出排污口固体边界和出水口边界条件对该过滤器的速度流场和压强场分布规律影响很大。

(3)滤网内外侧的水流流速沿X轴的分布不均匀，但由于出水口固壁边界条件条件的影响，上滤网水流的流速沿X轴的分布规律不同于下滤网，降低了网式过滤器的过滤效率；同时滤网内外侧较大的压强差，容易导致滤网变形，直至损坏，故减小流速和压强的不均匀分布有待进一步研究。

[1] 苏 荟.新疆农业高效节水灌溉技术选择研究[D]. 新疆石河子：石河子大学，2013.

[2] 孙 娟.河水滴灌重力沉沙过滤池的设计与应用推广[J].节水灌溉，2014,(1):60-64.

[3] 陶洪飞，邱秀云，李 巧，等.不同鳃片间距下的分离鳃内部流场三维数值模拟[J].农业机械学报，2014，45(6):183-189.

[4] 陶洪飞，邱秀云，赵丽娜，等.水沙分离鳃内部流场的数值模拟[J].农业工程学报，2013，29(17)：38-46.

[5] Tajrishy MA,Hills DJ, Tchobanoglous G. Pretreatment of secondary effluent for drip irrigation[J]. Journal of Irrigation and Drainage,1994,120(4): 716-731.

[6] 刘焕芳，刘 飞，谷趁趁，等.自清洗网式过滤器水力性能试验[J]. 排灌机械工程学报，2012，(2)：203-208.

[7] Avner Adin, Giora Alon. Mechanisms and process parameters of filter screens[J]. Irrigation and Drainage Engineering, 1996,293(4):112-115.

[8] Thokal R T, Raghavendra A G, Suresh N M, et al. Effect of sand particle size and concentration on performance of screen filter in trickle irrigation[J]. An-nals of Arid Zone, 2004,43(1):65-71.

[9] 宗全利，刘 飞，刘焕芳，等.滴灌用自清洗网式过滤器排污压差计算方法[J].农业机械学报，2012，43(11)：107-112.

[10] 刘焕芳，郑铁刚，刘 飞，等．自吸网式过滤器过滤时间与自清洗时间变化规律分析[J]．农业机械学报，2010，41(7)：80-83.

[11] 刘 飞，刘焕芳，宗全利，等.自清洗网式过滤器水头损失和排污时间研究[J].农业机械报，2013，44(5)：127-134.

[12] Wenyong WU, Wei CHEN, Honglu LIU, et al. A new model for head loss assessment of screen filters developed with dimensional analysis in drip irrigation systems [J]. Irrigation and Drainage, 2014 (63):523-531.

[13] 白兆亮，李 琳. 有压管道中孔板相对间距对局部阻力系数的影响及其机理研究[J].水电能源科学，2015，33(1)：177-182.

[14] 于 勇. FLUENT入门与进阶教程[M].北京：北京理工大学出版社，2010.

[15] 江 帆，黄 鹏. FLUENT高级应用与实例分析[M].北京：清华大学出版社，2010.