基于多指标的水安全评价模型研究
任永泰,姚继平,高春雨
(1.东北农业大学理学院,哈尔滨 150030;2.东北农业大学工程学院,哈尔滨 150030)
随着全球化进程的不断加快,人类赖以生存的自然环境尤其是水资源的安全受到了严重威胁,由第二届水论坛部长级会议提出的用水安全的呼吁[1],引起了广大学者们对水安全评价的研究。贾绍锋[2]等在分析水资源安全与水资源压力指数的基础上构建了层次分明的水安全评价指标体系。韩宇平[3]等利用多层次多目标决策和模糊优选理论建立的区域水安全评价的模糊优选模型有效地反映了各地区水安全状况。金菊良等[4]将基于加速遗传算法的模糊层次分析法与集对分析法相结合,建立的基于联系数的流域水安全评价模型在一定程度上提高了评价模型的可信度。刘生宝等[5]采用综合指数法对地下水饮水安全的评价很好地反映复杂的地下水安全情况。陈鸿起等[6]提出的基于欧氏贴近度的水安全综合评价模型减少了指标权重确定的主观性。娄梦筠[7]等采用指标规范值的灰色聚类方法对水安全进行评价,有效地减少了白化函数设计的工作量。
研究者们采用各种方法对水安全的研究取得了一定的成绩。然而,基于多指标的区域水安全评价模型中往往会存在许多指标信息冗余和对评价模型影响很小的评价指标,这会导致评价结果显著性和有效性不高。本文对多指标水安全评价体系构建评价模型,采用相关分析与主成分分析相结合的方法,消除评价体系中冗余的指标,以建三江水安全评价为例,运用熵权法求得建三江水安全系统安全指数,对多指标水安全评价具有重要的现实意义。
1 模型构建
1.1 建模思路
(1)将水安全评价指标标准化,计算出各指标之间的相关系数,评价指标两两之间的相关系数反映了它们之间的相关程度[8],为使评价指标体系更加简明有效,避免指标反映信息重叠,消除相关系数较大的指标中对评价不重要的指标。
(2)计算保留的评价指标的相关系数矩阵,利用该相关系数矩阵计算其特征值和特征向量,并将特征值按从大到小排序,通过计算主成分贡献率及累计贡献率确定主成分个数,然后依据确定的主成分得到每个评价指标的因子载荷。因子载荷大小表示评价指标对评价目标重要性的大小[9],为此,淘汰因子其绝对值小的评价指标,保证筛选出的指标对评价体系具有显著性影响。
(3)原始数据经过两次筛选得到最终的评价指标体系,对该评价指标体系构建隶属度矩阵,并对其进行标准化,然后通过标准化后的指标体系计算各个指标的信息熵和各个评价指标的信息熵权重。最后根据标准化的评价指标得分进行加权求和得到各个评价对象的综合得分,即为评价水安全的水安全指数。
1.2 建模步骤
1.2.1评价指标相关分析
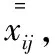
(1)
(3)
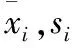
(2)计算相关系数矩阵R。
(4)
式中:rij=1(i=j),rij=rji。
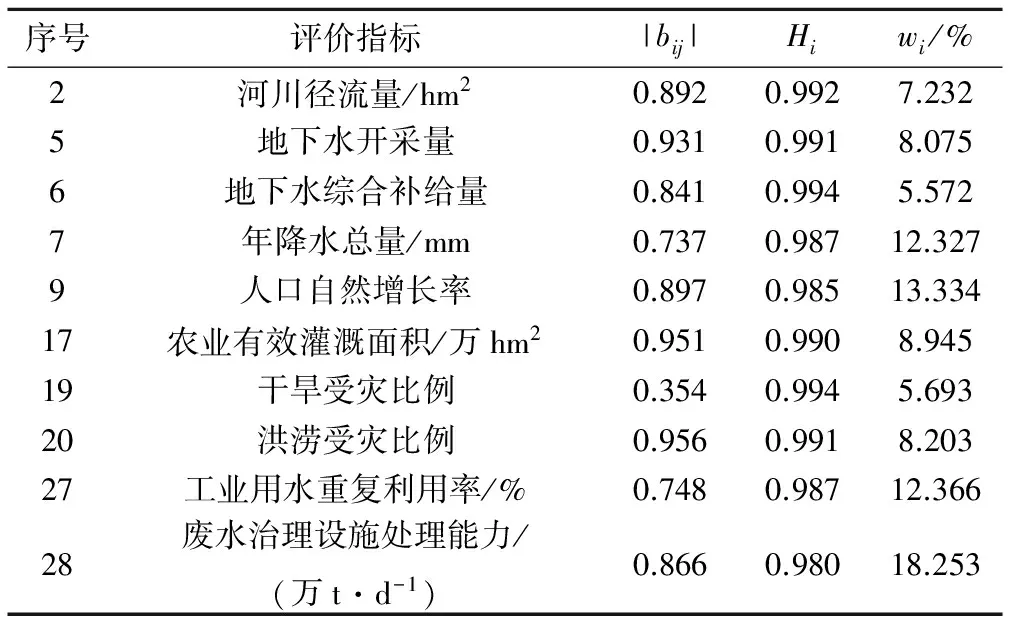
(3)规定一个临界值M(0 1.2.2评价指标主成分分析 (2)计算主成分贡献率及累计贡献率[11]。 主成分Fi的方差贡献率: (5) 式中:第i个主成分Fi的初始信息含量λi占全部原始信息含量的比例。 主成分Fi的方差累积贡献率: (6) 当第s个特征值对应的特征向量λs的累积贡献率αs≥85%时,则选前s个特征值所对应的主成分。 (3)主成分分析对评价指标的筛选。 (7) 因子载荷bij的大小影响指标对评价结果的显著性。因此,保留主成分Fi上的因子载荷|bij|大的评价指标。 1.2.3基于熵权法的综合得分 设m个评价指标,n个评价对象的实际数据构成数据矩阵X,X=(xij) ,表示第j个评价对象在第i个评价指标上的实际数据。 (1)数据标准化。采用式(1)的标准化公式对最终的评价指标体系中的指标进行标准化处理,再将标准化后的值都映射在区间[0,1]上,采用如下公式: (8) (2)计算评价指标的信息熵[12]。设Hi为第i个评价指标的熵值,n为评价对象的个数,则第i个评价指标的信息熵为: (10) (3)计算评价指标的熵权比重。设wi为第i个评价指标的熵权,m为评价指标的个数,则第i个评价指标的熵权为: (11) (4)计算评价对象的综合得分。设Pj为第j个评价对象的综合得分,则: (12) 建三江是中国最大的现代化农业生态园区,位于黑龙江、松花江、乌苏里江三江平原的东北部,土地面积1.235 万km2,该园区拥有15个大中型国有农场,总人口23万人,耕地面积约40万hm2,全区以水稻和大豆种植为主,主要依靠地下水灌溉,水资源丰富,秉承绿色农业,生产高效的理念,是目前我国农业机械化、现代化程度最高的地区。 本文参考《建三江年鉴》和《黑龙江省垦区年鉴》有关数据如表1所示,对建三江水安全进行评价分析。 表1 建三江水安全评价指标体系Tab.1 The water safety evaluation index system of Jiansanjiang 2.2.1建三江水安全评价指标相关分析 应用Matlab由式(1)和式(2)求得建三江水安全评价指标的相关系数矩阵R,并从中找出相关系数绝对值|R|>0.9的相关指标,再根据建三江水安全评价区域的实际情况,对处于同一相关度下的指标进行筛选,结果如表2所示。 表2 相关系数绝对值大于0.9评价指标的筛选Tab.2 The evaluation index screening of the correlation coefficient absolute value greater than 0.9 经相关分析,将保留的|rij|≥0.9的指标和|rij|≤0.9的所有指标作为相关分析后保留的评价指标,如表3所示。 2.2.2相关分析保留的评价指标主成分分析 由式(1)和式(4)计算筛选后保留的21个评价指标的相关系数矩阵R′,应用Matlab计算出R′的特征值λi(从大到小排序)和相应的特征向量ei,同时由式(5)和式(6)计算出Fi的zi和αs,选择αs为93.36%的前6个Fi,并根据式(7)计算出各个Fi中的bij,再从Fi中选择|bij|≥0.8的评价指标,其余Fi中选择|bij|最大的评价指标(见表4)。 表3 相关分析后保留的评价指标Tab.3 The reserved evaluation of the related analysis 表4 主成分的方差累积贡献率 % 表5 主成分分析后保留的评价指标Tab.5 The reserved evaluation of principal component analysis 运用熵权法,根据公式(8)~(12)计算最终得到的评价指标体系的信息熵Hi、熵权wi,如表5所示,最终求得建三江水安全指标的综合得分,即表6中的水安全指数Pj。 表6 建三江水安全评价安全指数Tab.6 The safety index of water safety evaluation 根据表6得出的水安全指数以及参照表7水安全评价标准,结果显示2002-2011年安全指数范围为0.442~0.600,建三江水安全系统整体上处于安全状态,这与建三江水安全系统的实际情况相符。 表7 城市水安全评价标准Tab.7 The criteria of urban water security evaluation 经过分析多指标水安全评价体系中存在冗余指标的问题,提出相关分析与主成分分析结合的方法,构建更加有效的评价指标体系,同时应运熵权法对水安全系统进行综合评价。以建三江地区为例,根据2002-2011年建三江地区影响水安全的各项指标的相关数据进行建模试验,结果显示,更加贴近该地区的实际情况,这表明本文的方法简化了评价模型的同时提高了整个评价体系的显著性和有效性,充分证明了该模型具有较高的实用价值。 [1] 方子云.提供水安全是21世纪现代水利的主要目标----兼介斯德哥尔摩千年国际水会议及海牙部长级会议宣言[J].水利水电科技进展, 2001,21(1):9-10. [2] 贾绍凤,张军岩,张士锋.区域水资源压力指数与水资源安全评价指标体系[J].地理科学进展, 2002,21(6):538-545. [3] 韩宇平,阮本清,解建仓.多层次多目标模糊优选模型在水安全评价中的应用[J].资源科学, 2003,25(4):36-42. [4] 金菊良,吴开亚,魏一鸣.基于联系数的流域水安全评价模型[J].水利学报, 2008,39(4):401-409. [5] 刘生宝,李晋杰,孙国才,等.基于综合指数的小城镇地下水饮水安全评价[J].环境科技, 2010,23(1):46-48. [6] 陈鸿起,汪 妮,申毅荣,等.基于欧氏贴近度的模糊物元模型在水安全评价中的应用[J].西安理工大学学报, 2007,(23):37-42. [7] 娄梦筠,刘志红,戴 睿,等.指标规范值的灰色聚类法用于水安全评价[J].成都信息工程学院学报, 2011,26(4):441-446. [8] 严丽坤.相关系数与偏相关系数在相关分析中的应用[J].云南财贸学院学报, 2003,19(3):78-80. [9] 李鸿禧.基于相关-主成分分析的港口物流评价研究[D]. 辽宁大连:大连理工大学, 2013. [10] 迟国泰,曹婷婷,张 昆.基于相关主成分分析的人的全面发展评价指标体系的构建[J].系统工程理论与实践, 2013,32(1):112-119. [11] 孙 慧,刘媛媛,张娜娜.基于主成分分析的煤炭产业竞争力实证研究[J].资源与产业, 2012,14(1):144-149. [12] 向红梅.区域水安全评价指标体系的构建与应用研究[D]. 广州:暨南大学, 2011.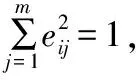
2 实例分析
2.1 建三江概述
2.2 建三江水安评价指标体系建立


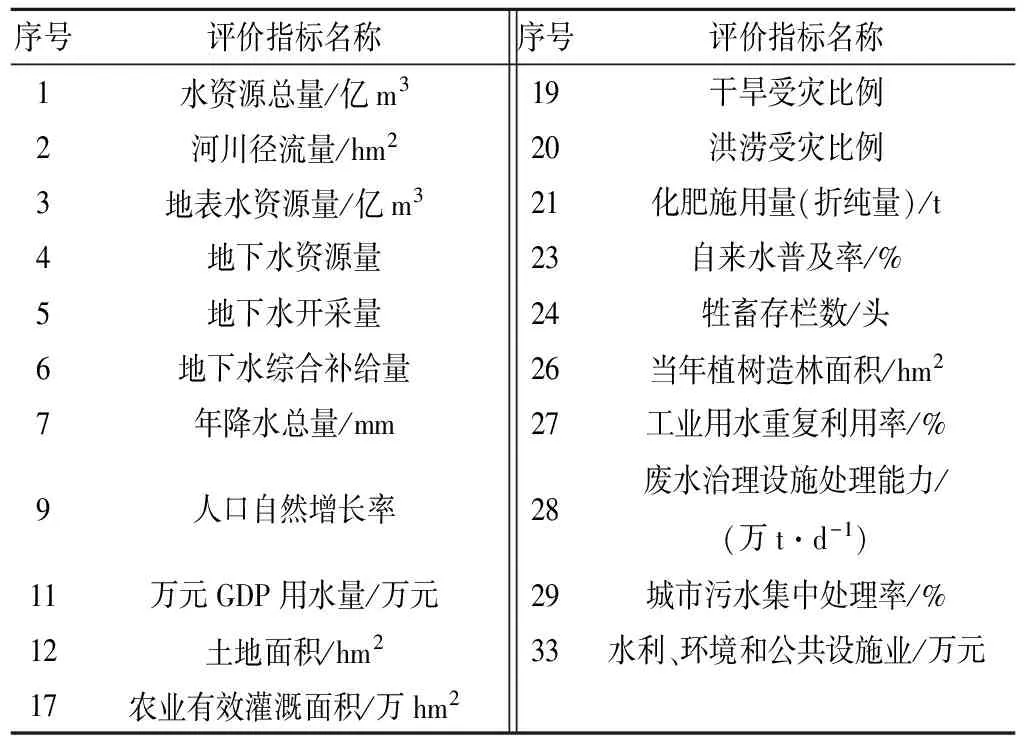

2.3 建三江水安全评价及结果分析


3 结 语

