基于主成分分析的土壤凋萎系数BP预测模型

于 浕，樊贵盛

(太原理工大学水利科学与工程学院，太原 030024)

凋萎系数通常被视为作物有效含水量的下限，是作物开始发生永久凋萎时的土壤含水率[1]，也是进行作物水分调控和田间用水管理的重要参数。准确确定土壤凋萎含水率对于制定合理的灌溉制度，实现节水增产具有重要的指导意义。目前，测定土壤凋萎系数的常用方法分为直接法和间接法。直接法就是在实验室中用生物方法测定；间接法是先测出土壤的吸湿系数,再乘以1.5(或2)[2]。两种方法测定土壤凋萎系数费时费力，而且由于土壤空间变异性大和缺乏精密仪器，使得在农业生产中的应用受到限制。近年来，国内外众多学者致力于利用土壤常规理化参数对土壤凋萎系数预测的研究，取得了显著成果。Pidgeon[3]在分析土壤中微粒级分布的基础上得到了凋萎系数与黏粒含量的线性拟合模型。赵广建、樊贵盛[4]通过对不同有机质含量条件下土壤凋萎系数的试验研究，得到了土壤凋萎系数与有机质的定量函数关系。李任敏[5]等实现了利用土壤机械组成对9种阔叶乔灌树苗期凋萎系数的初步预报。李小刚[6]建立了利用土壤黏粒含量、电导率、全盐量对土壤凋萎系数的线性预报模型，但未考虑有机质等其他重要因素的影响，并且所建模型预测精度尚需进一步提高。

因此，本文在前人研究的基础上，从土壤理化参数与凋萎系数存在非线性关系出发，采用主成分分析法，提取影响因子的特征数据以降低输入变量维数，减少输入层神经元个数，并运用BP神经网络模型在表达非线性、不确定性和模糊关系等方面的强大优势，实现了利用土壤常规理化参数对土壤凋萎系数的多因子预测，在优化神经网络结构和提高预测精度的同时，为黄土高原区作物水分调控和田间用水管理提供了科学依据。

1 样本的获取

1.1 土壤条件

试验土壤选自山西省中南部多个典型试验田，土壤样本特征明显，质地类型丰富，涵盖多种地形地貌单元，是山西省黄土高原区农田耕作土壤的典型代表。试验点土壤样本数据取值范围如表1所示。

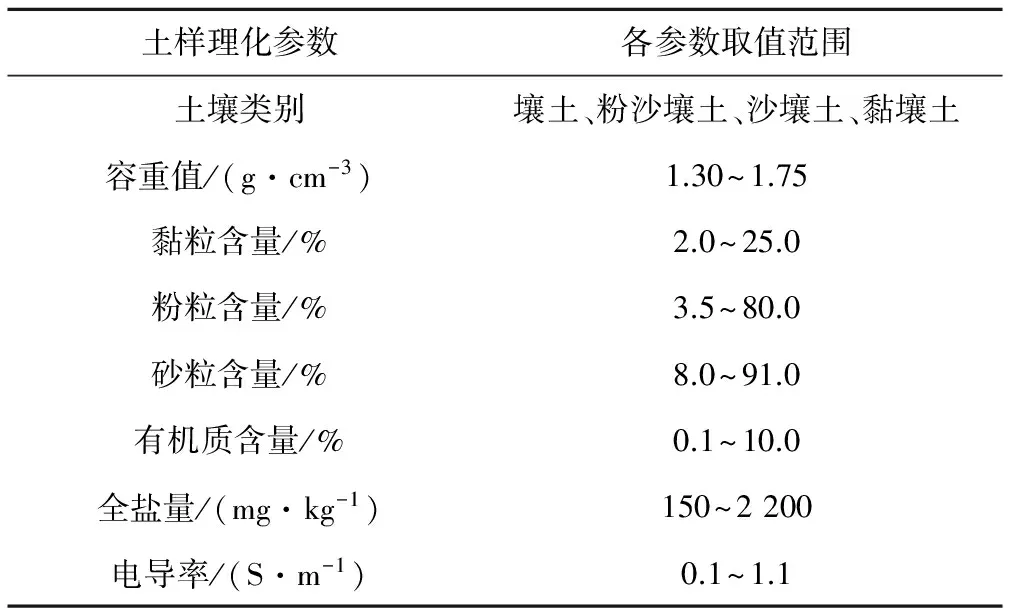
表1 样本数据取值范围表

1.2 试验方案

为了实现本文的研究目的，需要对样本土壤进行基本理化参数和凋萎系数的测定。测定的土壤基本理化参数有土壤质地、土壤有机质含量、土壤无机盐含量。利用激光粒度分析仪测定样本土壤黏粒、粉粒、沙粒的百分比含量，由此确定土壤质地类型。测定土壤有机质含量采用重铬酸钾滴定法，利用浓硫酸和重铬酸钾迅速混合时产生的热来氧化土壤中的有机质，过剩的重铬酸钾溶液用硫酸亚铁标液滴定，进而依据消耗的重铬酸钾量计算土壤中有机质的含量，通过测定土壤中八大主要离子的质量，累加后得到土壤全盐量[2]。

测定土壤样本吸湿系数采用10%硫酸溶液水气平衡吸附法[2]。将风干土样过 1 mm筛后称量10 g平铺在铝盒底部,分别进行称重并编号。将铝盒放置于盛有10%硫酸干燥器的白瓷板上, 加盖密闭并放在温度恒定的地方。每隔24 h用精度为 0.000 1 g 的电子天平称重,控制前后两次称量质量差值在0.05 g范围内，然后进行烘干称重测得土壤的含水量,得到土壤吸湿系数,乘以1.5后得到土壤样本的凋萎含水率。

1.3 样本数据的建立

随机选取的10组取自不同试验田的土样，测得的凋萎含水率(体积含水率)数据和对应样本下土壤的物理性黏粒含量、有机质质量分数、全盐量和电导率等基本理化参数如表2所示，在全部试验数据资料中选取100组具有代表性的土壤样本数据来建立预测模型，并随机预留10组数据用以检验模型精度。

2 BP神经网络模型的建立

2.1 凋萎系数主成分分析

主成分分析是一种常用的多元统计分析法。该方法将多个相关变量进行线性组合后形成新的正交变量，使这些不相关的新变量尽可能多地反映原变量的数据信息[7]。原始变量的数据信息主要体现在方差上，并通过累积方差贡献率衡量。

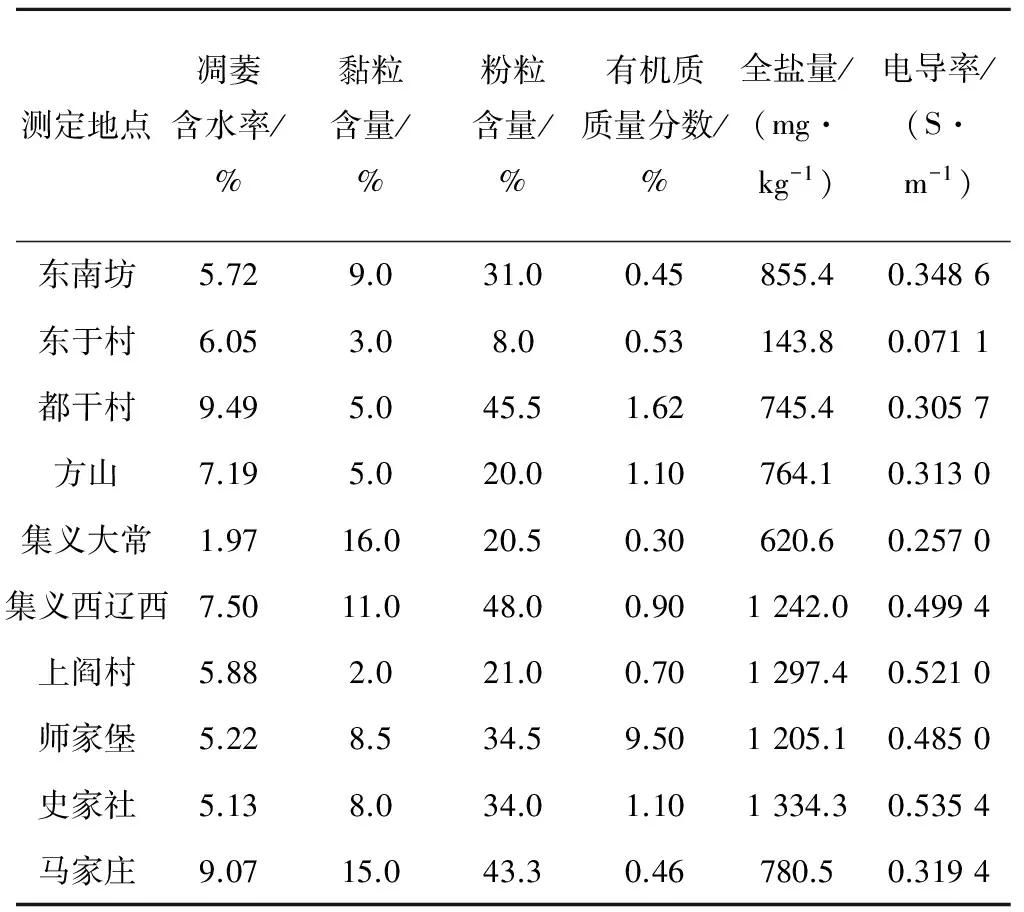
表2 10组试验点样本数据

影响土壤凋萎系数的因素有密度、黏粒含量、粉粒含量、沙粒含量、有机质含量、全盐量和电导率等基本理化参数[6,8-10]，从全部试验数据中选取10组典型试验站测得的数据进行主成分分析。按照先标准化处理得到相关系数矩阵R，再求解R的特征值、特征向量以及方差贡献率等步骤进行计算，并依据累积方差贡献率提取主成分，当累积方差贡献率大于等于85%时，便认为对应的前n个主成分便包含全部全部原始数据的绝大部分信息。表3为特征值及方差贡献率按大小排列的数据表。

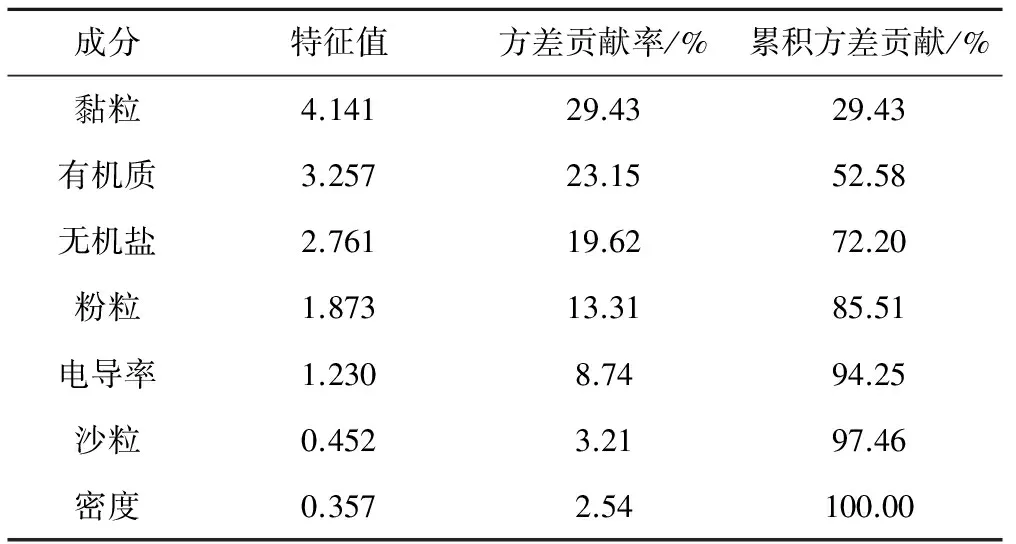
表3 特征值及方差贡献率数据表

根据主成分分析得到的结果确定预报模型的输入因子。因此，选定土壤黏粒含量、有机质含量、全盐量和粉粒含量作为预报模型的输入因子。

当土壤颗粒表面的薄膜水受土壤介质吸着力达到155 m水柱高时，土壤中的水分便不能被植物根系所利用，所以土壤凋萎含水率与土壤比表面积关系密切。分析认为，土壤的物理性黏粒和粉粒含量越多,其比表面积就越大,土壤的凋萎系数也就越大。土壤有机质含量和全盐量对凋萎系数的大小影响显著且影响机理类似，随着土壤中有机质和无机盐含量的增加，土粒表面的土壤水势降低, 土壤颗粒对水的吸附作用显著增强，则在土粒表面吸着的水膜厚度增大,土壤的凋萎系数也随之增大。

选定农田耕作土壤凋萎系数的预测值作为预报模型的输出因子，通过比较预测值与实测值的误差来检验所建模型的预测精度。

2.2 BP神经网络的设计方法

(1)BP神经网络的设计层数。BP神经网络是目前人工神经网络中较为成熟且应用最为广泛的神经网络模型，一般具有3层或3层以上的神经网络结构[11]。本文所建立的BP神经网络系统由输入层、中间隐含层和输出层3部分构成。

(2)BP神经网络各层中的神经元个数。预报模型有4个输入参数，1个输出参数，即输入层有4个神经元，输出层有1个神经元；中间隐含层神经元的数目需要多次迭代计算才能确定，通过逐渐增加隐含层节点数，反复训练样本，直到达到模型的目标精度时训练停止[12]。依据既满足精度要求又减少训练次数的原则,在多次迭代计算后得出,当模型隐含层的神经元个数等于15时训练精度满足要求，故建立比例为4∶15∶1的网络拓扑结构。

(3)BP神经网络训练参数设置。基于Matlab7.0神经网络工具箱中newff函数，在分析所要处理的数据后，选择trainlm函数为模型的训练函数，并利用归一化函数premnmx和还原函数postmam来实现对输入和输出样本的归一化处理，以加快样本的收敛速度。基于归一化处理后数据的特性，选择正切函数tansig作为隐含层的激活函数，线性purelin函数作为输出层的激活函数[13]。本文所训练的模型参数设定为:最大学习迭代次数1 500次，学习率为1%，训练精度为0.05%。

(4)BP神经网络的工作原理。BP神经网络模型又称多层前馈神经网络，由前向传播和后向传播构成。信息经过输入层输入神经网络后，通过中间隐含层神经元的逐层传递，最终在输出层得出输出变量，比较输出变量值与期望输出值，若两者满足允许的误差，则计算结束，若两者误差超过允许误差，则将误差进行反向逐层传回输入层，同时调整各层权值，在不断迭代计算中，使得误差满足目标允许的范围，最后得到准确的输出值[14]。

2.3 农田土壤凋萎系数预报模型

本文建立的BP网络模型结构如式(1)所示。

net=newff(min max (trainput),[15,1],

{‘tansig’, ‘purelin’}, ‘trainlm’)

(1)

式中：net为本文所创建的BP神经网络模型；newff为在Matlab7.0中生成的BP神经网络函数；min max( )为向量矩阵，用以决定输入参数的取值范围；15表示隐含层有15个神经元，1表示输出值有1个，即农田土壤凋萎系数；{‘tansig’, ‘purelin’}分别为隐含层和输出层的激活函数形式；‘trainlm’为网络的训练函数形式。

BP神经网络的训练结果如式(2)所示。

θ=purelin(iw2(tansig(iw1p+b1))+b2)

(2)

p=[γ,δ,β,φ]

(3)

式中：θ表示凋萎含水率；iw1是模型输入层到隐含层的权值；iw2是模型隐含层到输出层的权值；b1是模型输入层到隐含层的阈值；b2是模型隐含层到输出层的阈值；γ为物理性黏粒含量；δ为粉粒含量；β为土壤有机质含量；φ为土壤全盐量。

表4为农田耕作土壤凋萎含水率的预测模型矩阵数值表。

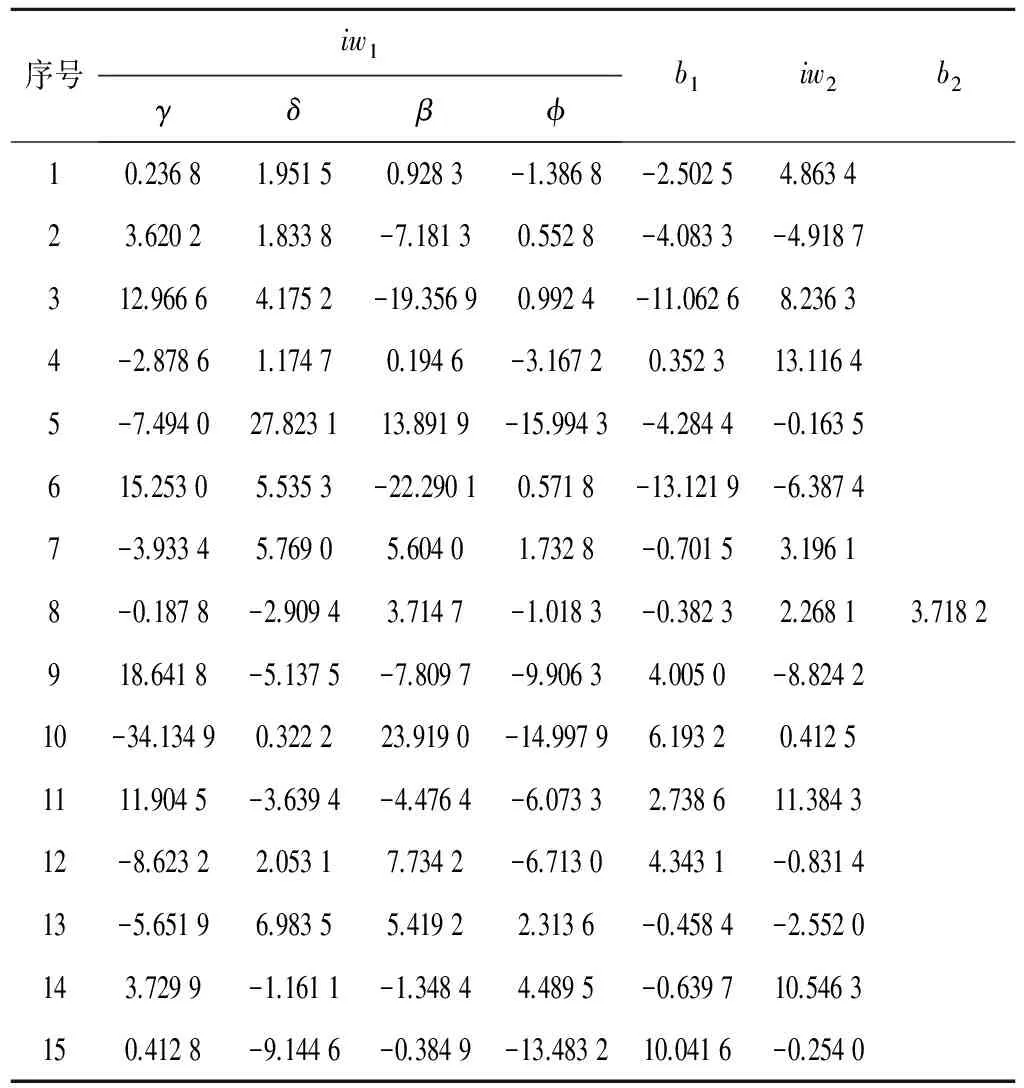
表4 BP预报模型矩阵数值表

3 BP模型的预测结果与精度检验

基于Matlab7.0中得到的BP模型对100组耕作土壤凋萎系数的预测值，计算预测值与实测值的绝对误差和相对误差，结果如表5所示。

表5 凋萎系数预测值与实测值的误差分析表 %

根据Matlab7.0中BP预测模型程序运行的结果得出：当训练步数为354步时，训练精度达到0.000 498 991，满足训练目标精度0.000 5的要求，说明建模所用100组数据的预测值与实测值基本吻合，其绝对误差平均值为0.166%，绝对误差最大值为0.681%，绝对误差最小值为0.000 4%；其相对误差平均值为2.837%，相对误差最大值为12.549%，相对误差最小值为0.007%。通过比较100组土壤凋萎系数实测值与预测值的误差，我们得出，本文选择土壤黏粒含量、粉粒含量、有机质含量和全盐量作为输入参数建立预测模型是合理的，所建模型误差小，预测结果可信度高，可以作为农田耕作土壤凋萎系数的预报模型。用随机预留的10组数据检验模型的预测精度，检测结果如表6所示。

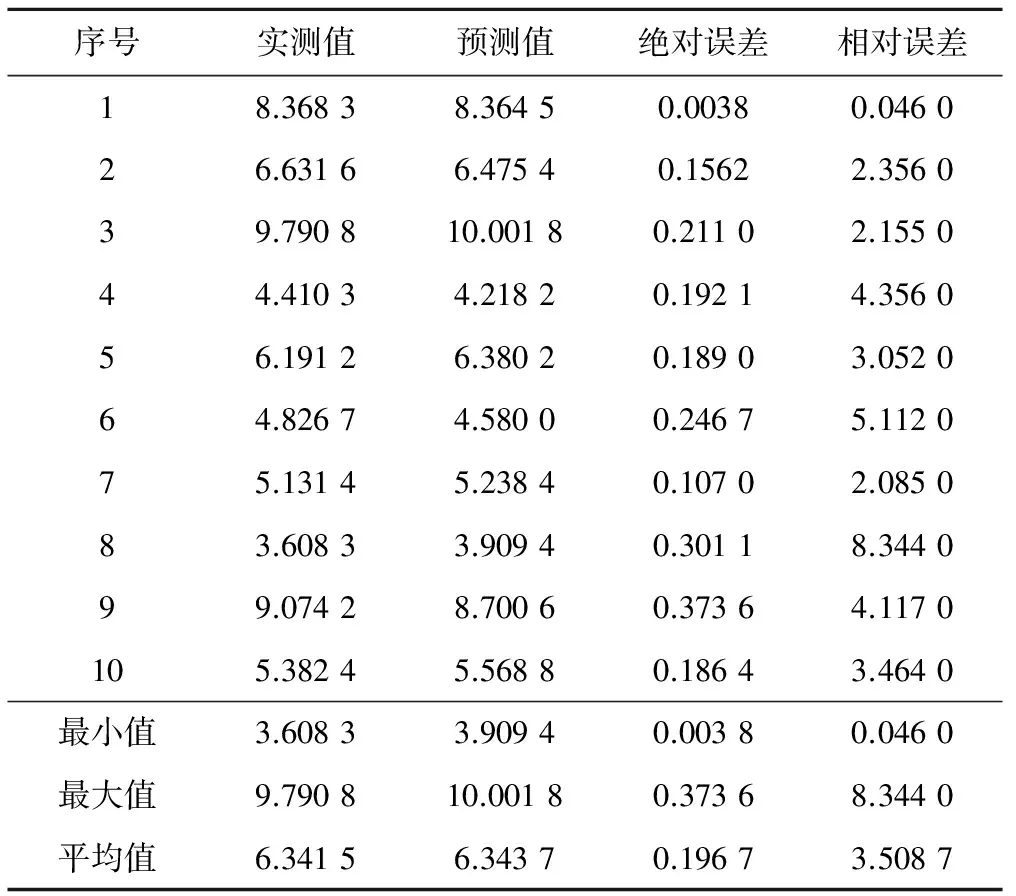
表6 土壤凋萎系数预测精度检验表 %

用随机预留的10组数据检验模型的预报精度,可以看出，绝对误差最大值为0.373 6%，最小值为0.003 8%，平均值为0.196 7%；相对误差最大值为8.344%，最小值为0.046%，平均值为3.508 7%，在可接受的范围，结果表明利用土壤基本理化参数预报农田耕作土壤的凋萎系数是可行的，可以为农业生产提供强有力的理论与技术支撑。

4 结 语

(1)利用土壤常规理化参数对农田耕作土壤凋萎系数的预测是可行的。将土壤物理性黏粒含量、粉粒含量、有机质含量和全盐量作为BP模型的输入变量来预测土壤凋萎系数是合理的。比较100组耕作土壤凋萎系数的实测值与预测值，其绝对误差和相对误差的平均值分别为0.166%和2.837%，预留10组检验样本的绝对误差和相对误差平均值分别为0.196 7%和3.508 7%，误差较小，预测精度较高。这实现了利用土壤常规理化参数对土壤凋萎系数的有效预测，为作物水分调控和田间用水管理提供了重要的理论依据。

(2)本文所建立的基于主成分分析的BP神经网络预报模型达到了预期成效。通过对原始输入因子的主成分提取，有效降低了输入样本的维数，减少了输入层神经元个数，优化了模型结构，加快了迭代速率，提高了预测精度，在丰富土壤理化参数预测理论的同时，也为今后预测、聚类回归等方面的研究提供了一种新方法。

[1] 雷志栋,杨诗秀,谢传森.土壤水动力学[M].北京：清华大学出版社,1988.

[2] 张明炷.土壤学与农作学[M].北京:中国水利水电出版社,1994.

[3] Pidgeon J D. The measurement and prediction of available water capacity of ferrallitic soils in Uganda[J].Journal of Soil Science,1972,23(4):431-441.

[4] 赵广建,樊贵盛.凋萎系数与土壤有机质含量的定量关系研究[J].山西水土保持科技，2008,3(1):12-13.

[5] 李任敏,吕 皎,李莲枝.土壤机械组成对苗木凋萎系数的影响初报[J]. 山西林业科技，1990,(3):29-31.

[6] 李小刚.甘肃景电灌区盐化土壤的吸湿系数与凋萎湿度及其预报模型[J]. 土壤学报，2001,38(4):498-505.

[7] 王 华,王连华,葛岭梅.主成分分析与BP神经网络在煤耗氧速度预测中的应用[J].煤炭学报,2008,33(8)：920-925.

[8] 乔照华.土壤凋萎系数的影响因素研究[J].水资源与水工程学报，2008,19(2):82-85.

[9] Petersen G W, R L Cunningham, R P Matelski.Moisture characteristics of Pennsylvania soils, I. moisture retention as related to texture[J].Soil Science Society America Journal,1968,32(2):271-275.

[10] Lund Z F. Available water-holding capacity of alluvial soil in Louisiana[J].Soil Sci. Soc. Am. Proc.,1959,23:1-3.

[11] 赵西宁,王万忠,吴普特，等.坡面入渗的人工神经网络模型研究[J].农业工程学报,2004,20(3):48-50.

[12] 伍春香,刘 琳,王葆元.三层BP网隐层节点数确定方法的研究[J].武汉测绘科技大学学报,1999,(2):85-87.

[13] 尹京川,马孝义,孙永胜,等.基于BP神经网络与GIS可视化的作物需水量预测[J].中国农村水利水电,2012,(2):13-15,18.

[14] 何 勇,宋海燕.基于神经网络的作物营养诊断专家系统[J].农业工程学报,2005,21(1):110-113.