蓄水坑灌条件下苹果树茎流速率的BP神经网络模型

秦 聪，孙西欢,2，郭向红，马娟娟，桑永青，李 波

(1.太原理工大学水利科学与工程学院，太原 030024; 2.山西水利职业技术学院，山西 运城 044004)

0 引 言

蓄水坑灌法[1]是孙西欢教授针对北方山丘区果林提出的一种灌溉新方法，该方法同时兼具了节水、保水、抗旱等诸多优点，并且可以充分利用降雨、抑制水土流失[2]。目前为止，学者们对蓄水坑灌已有一定的研究：根据蓄水坑灌坑内水头和边界的特点，马娟娟等[3]建立了多坑复杂边界条件下土壤水分运动数学模型，郭向红等[4]建立了蓄水坑灌单坑土壤水分运动的数学模型；考虑到氮肥带来的环境污染和作物的优质生产，李京玲等[5]建立了蓄水坑灌单坑土壤水氮运移的数值模型；为提高土壤水分利用率，崔世勇等[6]分析了蓄水坑灌条件下不同坑深的土壤水分分布特征；迄今为止，对蓄水坑灌条件下茎流方面的研究，只有仇群伊[7]通过热扩散茎流计(TDP)测得树干茎流量，分析了蓄水坑灌条件下苹果树树干茎流量的变化规律，并且把树干茎流量和相关的影响因子进行了简单的拟合。

灌溉制度是为了保证作物的高效、高产所制定的农田灌水方案，包括作物生产周期内的灌水定额、灌溉定额和灌水次数，即制定不同时期的农田水分消耗。农田水分消耗中的作物需水量即作物蒸腾对作物的生长发育和灌溉制度的建立起着决定性的作用。蒸腾是植物体内的水分通过植物表面进入大气的过程，是土壤-植物-大气连续体(SPAC)的重要环节，不仅可以降低植物的温度，其产生的拉力还可促进根系吸收水分。而植物靠根系从土壤中吸收的水除了很少一部分参加各项生命活动，绝大部分用于蒸发蒸腾，而植物蒸腾与茎流之间存在着非常高的相关关系[8]。诸多学者[9-12]对香梨、玉米等植物的茎流速率与环境因子进行了大量的线性回归分析，但利用气象因子对苹果树的茎流速率进行高精度预测的研究甚少，而且茎流计及其配套设备价格较高，难以大面积推广。因此，用较易获得的气象因子对苹果树茎流速率进行预测，不仅预测精度高，而且省钱、省时、省力，对苹果树灌溉制度具有实际的指导意义。本文建立了蓄水坑灌条件下苹果树茎流速率的BP神经网络模型，旨在为制定蓄水坑灌条件下灌溉制度提供可靠依据，进一步完善和推广蓄水坑灌法。

1 BP神经网络模型

BP(Back Propagation)神经网络模型[13-15]起源于1986年，其是由输入层、隐层和输出层所组成的，也是目前比较成熟、效果最好、应用最广泛的神经模型之一。其工作原理为：当信息正向传播时，输入层将输入信息传递给隐含层各个神经元，隐含层经过一系列处理后，由输出层输出结果。如若输出结果达不到预期，则进行误差的反向传播，即将误差由输出层向隐含层和输入层传播，并且依次调整各层的连接权，最终返回输出层。按此过程循环直至达到预期结果后，终止训练。

其训练过程如下：(1)设定BP神经网络的输入节点、隐层节点、输出节点的个数分别为i，j，k。输入层到隐含层的权值为wlm,l=1,2,…,i,m=1,2,…,n，阈值为w=[w1,w2,…,wj]；隐含层到输出层的权值为un，n=1,2,…,k，阈值为u=[u1,u2,…,uk]。

(2)隐含层输出。

式中：f为输入层到隐含层的传输函数;xl为第l个输入节点。

(3)输出层输出。

(4)误差计算。

式中：tgn是当输出节点为n时，在样本g的作用下的期望输出值，同理，qgn为计算输出值；N为样本数。

当E≤e(e为计算期望精度)时，则终止计算；否则，将进行误差的反向传播。

(4)权值更新。

其中，η为学习率。

(5)阈值更新。

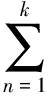
un(v+1)=un(v)+(tn-qn)

图1 BP神经网络结构图

BP神经网络模型能够反映变量之间复杂的非线性关系，具有自组织、自学习等能力，尤以模型识别、数据分类、数据压缩等功能较为突出。基于其算法简单、预测精度高等特点，BP神经网络模型成为众多领域应用的首选模型。

2 茎流速率神经网络模型的建立

(1)输入层和输出层。输入层选取气象因子辐射强度、相对湿度、土壤温度、温度及风速作为输入变量，输出层为预测茎流速率。

(2)隐层的确定。BP神经网络模型是由输入层、隐层和输出层组成的多层前馈网络。隐层数[16]的增加会提高预测精度，但同时会使网络结构复杂化、增加网络训练时间，甚至出现“过拟合”等现象，而Robert Hecht Nielson[17]对神经网络的研究中发现，一个隐层的BP神经网络可以对任何闭区间内的连续函数逼近。因此，本研究采用3层BP神经网络模型对茎流速率进行预测。

(3)传输及训练函数的确定。本文采用连续可微、能够反应非线性特征、运算速度快、结构简单的正切tansig函数 作为输入层的传输函数，线性函数purelin作为输出层的传输函数。选取训练速度快的trainlm函数作为训练函数。

(4)隐层节点数的确定。隐层节点数的选取对神经网络性能及预测效果影响很大，为避免出现泛化能力下降和“过拟合”等问题，Kolmogorov、Jadid和Fairbairn、张清明、高大启等[18]提出了许多选取隐层节点的经验公式，但目前尚无一个普遍和科学的理论方法。本文中采用扩张法反复进行训练，直至达到对误差和结构的要求为止。

(5)模型参数的确定。本文选择的学习率为0.01，这样可以确保模型在学习过程的收敛性；选择的最大训练次数为1 000；为保证模型拟合度高，选择训练目标为0.000 1。

BP神经网络模型中的函数及参数如表1所示。

表1 BP神经网络模型中的函数和参数

3 实例验证

3.1 蓄水坑灌茎流速率数据采集

试验在位于山西省太谷县西南部的山西省农科院果树研究所矮化果园中进行，试验区为南北向，果树行株距为4 m×2 m，灌溉水源为地下水，试材为7年生红富士长富二号矮化砧处理苹果树。

蓄水坑灌法是将水注入到蓄水坑中，通过坑壁向四周渗水，将水直接送到果树根须处。每株果树设置4个蓄水坑，蓄水坑距离树干60 cm，坑深40 cm，直径30 cm，并且采用与蓄水坑形状一致、桶壁均匀分布2 mm孔径出水口的圆形不锈钢铁桶进行固壁。4个蓄水坑之间通过环状沟连接，环状沟深度为10 cm，宽度为30 cm，如图2所示。

图2 蓄水坑灌法田间工程示意图

茎流速率采用TDP插针式植物茎流计进行监测，每半小时自动采集一次；气象因子采用Adcon_Ws无线自动气象监测站进行监测，每15 min自动采集一次，监测的指标包括辐射强度、相对湿度、温度、土壤温度及风速等。

从大量的茎流数据中，随机选取255组数据。其中245组为BP神经网络模型的训练样本，10组为检验样本。

3.2 隐层节点数的确定

本文在根据经验公式确定出隐层节点数的范围的基础上，将其放大，通过不断调整节点数与比较训练目标方差确定最优隐层节点数，如表2所示。

由表2可知，当隐含层节点数变化在10～30，模型完成了最大训练次数1 000次，但是训练目标均方差均大于训练目标0.000 1，无法满足训练要求，模型不收敛；在模型收敛的情况下，训练目标均方差在9×10-5以下的模型对应的节点数为46～49，而隐层节点数为46时对应的训练目标均方差最小、训练次数最少，且模型训练曲线较为光滑。因此，BP神经网络模型的隐层节点数选为46，其训练曲线如图3所示。

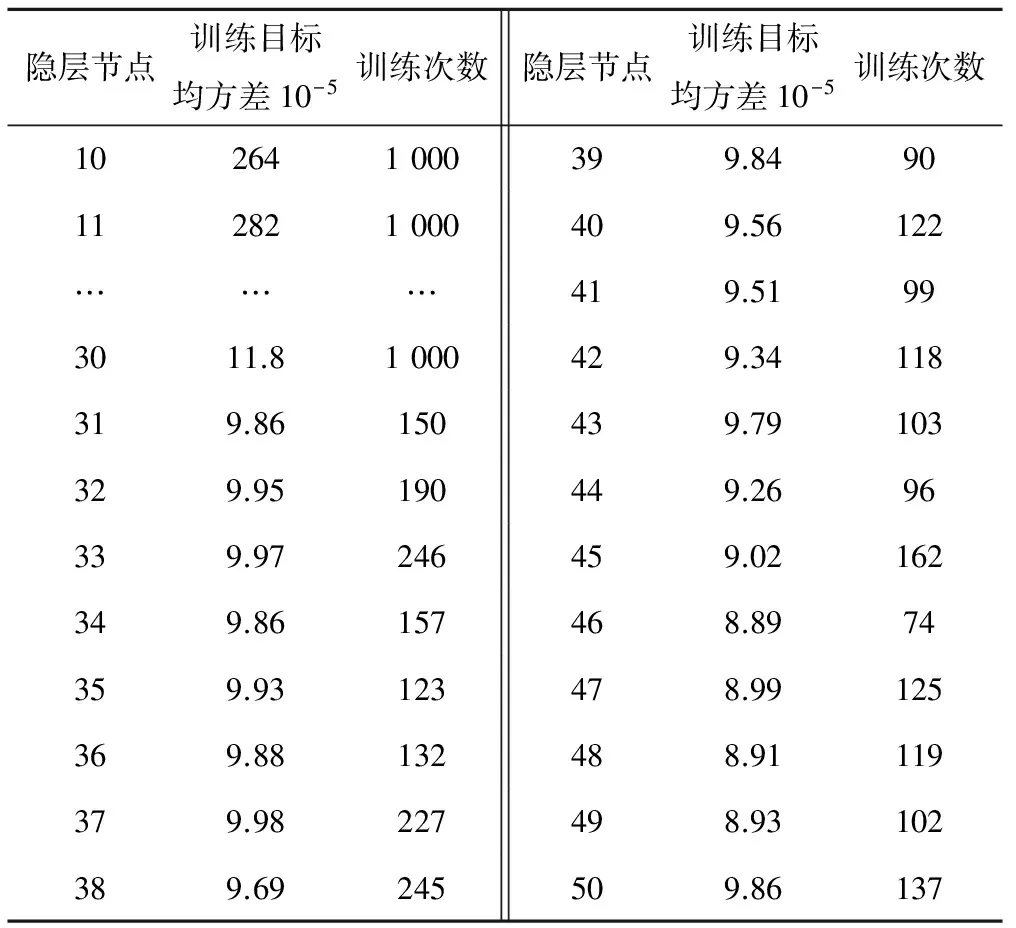
表2 隐层节点数的确定

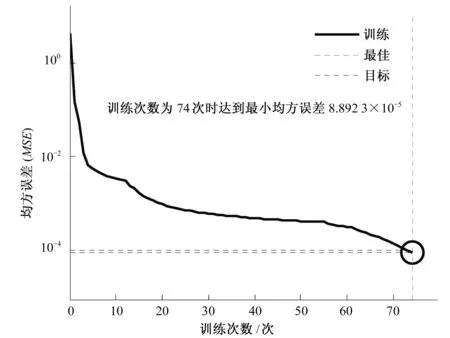
图3 隐层节点数为46时的训练曲线

3.3 模型评价

(1)模型的训练结果。经过对模型函数、参数和隐层节点数的确定，以试验区245组数据作为建模样本，BP神经网络模型部分训练结果(50组)如表3所示。

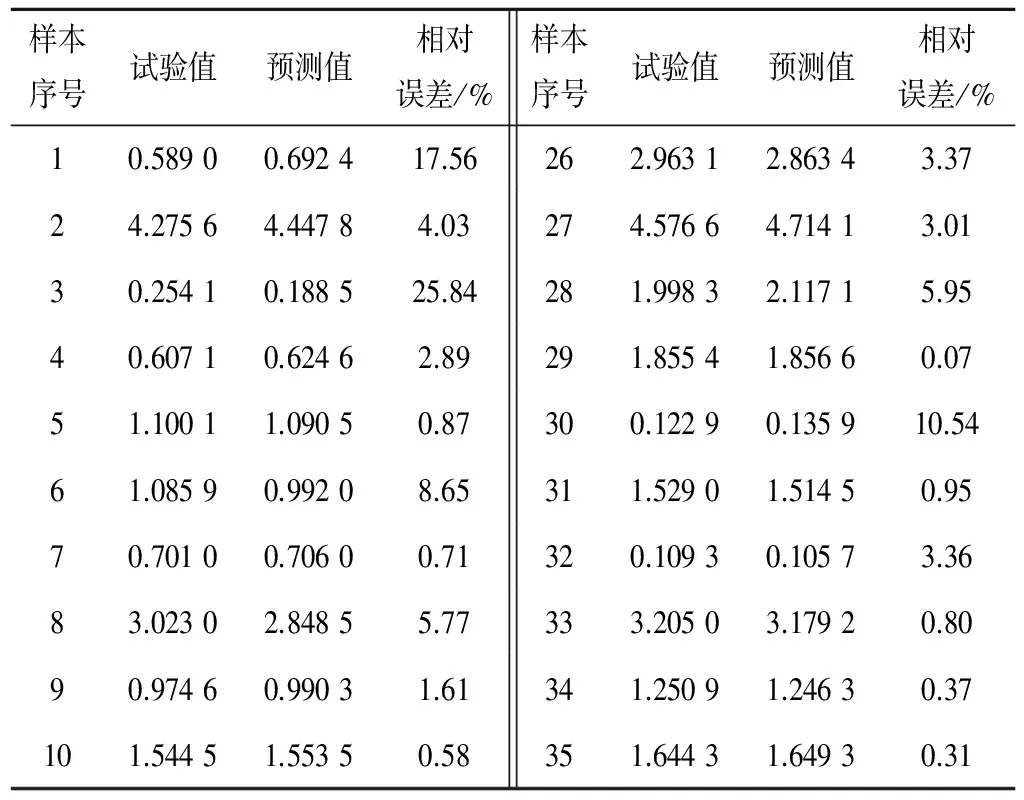
表3 BP神经网络模型的训练结果

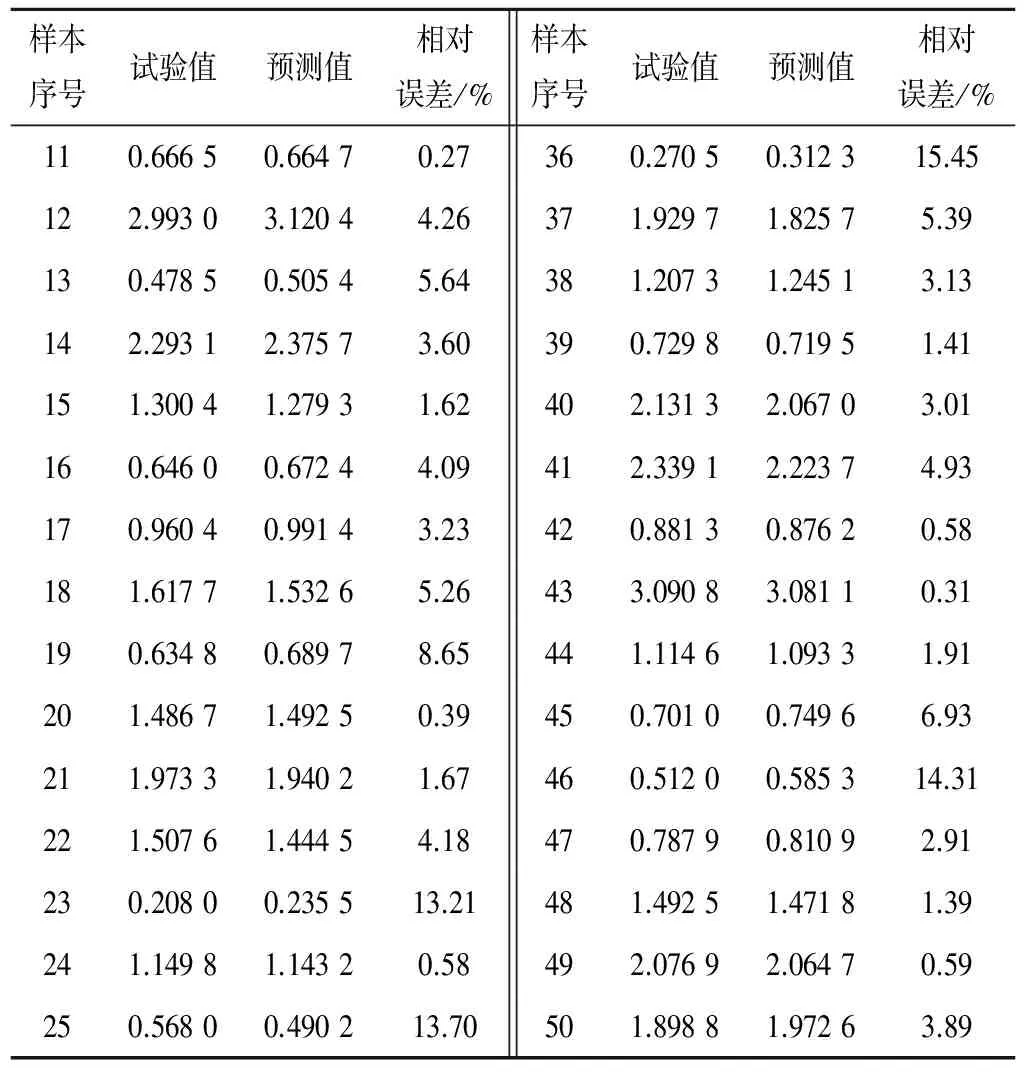
续表3 BP神经网络模型的训练结果

(2)模型的显著性检验。给定显著水平α=0.05，通过计算获得相应的F值，若F>F0.05，则预测模型显著，反之，则不显著，检验结果如表4所示。

表4 模型显著性检验

图3 训练数据拟合效果

由表4及图3可知，F>>F0.05，拟合度为0.998 0，平均相对误差仅为4.4%，说明BP模型显著性强，训练曲线拟合度好，模型预测精度高。

3.4 检验评价

以未参与建模的10组数据代入上述BP神经网络模型对茎流速率进行预测，其试验样本及预测结果如表5所示。

由表5可知，茎流速率的相对误差在0.34%～3.30%范围内变化，满足预测精度要求。由此可见，以辐射强度、相对湿度、土壤温度、温度及风速作为输入变量，采用BP神经网络法，对蓄水坑灌条件下的茎流速率进行预报是可行的。

表5 预报实例

图4 检验数据拟合效果

4 结 语

本文选取辐射强度、相对湿度、土壤温度、温度及风速作为主要因子，建立了蓄水坑灌条件下苹果树茎流速率的BP神经网络模型，并且用未参与建模的数据代入该模型预测苹果树茎流速率，取得了较为理想的结果。因此，使用BP神经网络对蓄水坑灌条件下茎流速率进行预测是可行的，为蓄水坑灌条件下的灌水制度提供了科学合理的依据。

[1] 孙西欢. 蓄水坑灌法及其水土保持作用[J]. 水土保持学报, 2002,16(1):130-131.

[2] 孙西欢. 蓄水坑灌法技术要素初探[J]. 沈阳农业大学学报, 2004,35(5-6):405-407.

[3] 马娟娟,孙西欢. 蓄水多坑入渗条件下土壤水分运动建模与试验[J]. 农业机械学报, 2010,41(3):46-51.

[4] 郭向红,孙西欢. 蓄水坑灌单坑土壤水分运动有限元模拟[J]. 农业工程学报, 2007,23(10):1-5.

[5] 李京玲,马娟娟. 蓄水坑灌单坑土壤氮素迁移转化的数值模拟[J]. 农业工程学报, 2012,28(1):111-117.

[6] 崔世勇,孙西欢. 蓄水坑灌不同坑深条件下土壤水分分布特征分析[J]. 节水灌溉, 2014,(5):14-17.

[7] 仇群伊. 蓄水坑灌条件下苹果树蒸发蒸腾特性研究[D]. 太原：太原理工大学, 2014:31-40.

[8] 庞鸿宾. 节水农业工程技术[M]. 郑州: 河南科学技术出版社,2000.

[9] 刘 浩,孙景生. 温室滴灌条件下番茄植株茎流变化规律试验[J]. 农业工程学报,2010,26(10):77-82.

[10] 李 会,刘 钰. 夏玉米茎流速率和茎直径变化规律及其影响因素[J]. 农业工程学报,2011,27(10):187-191.

[11] 张清林,马英杰. 滴灌条件下核桃树茎流变化规律研究[J].灌溉排水学报,2012,31(1):62-65.

[12] 刘洪波,张江辉. 干旱区香梨茎流特征及其与环境因子的关系[J].节水灌溉.2014,(11):25-28.

[13] 焦李成. 神经网络系统理论[M]. 西安:西安电子科技大学出版社, 1990.

[14] 罗成汉. 基于MATLAB神经网络工具箱的BP网络实现[J]. 计算机仿真, 2004,21(5):109-112.

[15] 李 萍,曾令可. 基于MATLAB的BP神经网络预测系统的设计[J]. 计算机应用与软件, 2008,25(4):149-151.

[16] 严 鸿,管燕萍. BP神经网络隐层单元数的确定方法及实例[J]. 控制工程, 2009,(16):100-103.

[17] Kok JR, Vllassis N. Mutual modeling of teammate behavior[D]. Amsterdam: University of Amsterdam, 2002.

[18] 张清良,李先明. 一种确定神经网络隐层节点数的新方法[J]. 吉首大学学报, 2002,23(1):89-91.