岩心加压饱和地层水时间计算方法

苏广乐　李晓平　袁 淋　杜唐钟

(1. 西南石油大学油气藏地质及开发工程国家重点实验室， 成都 610500；

2. 中石化西南油气分公司川东北采气厂, 四川 阆中 637400；3. 长庆油田第十采油厂, 甘肃 庆城 745100)



岩心加压饱和地层水时间计算方法

苏广乐1李晓平1袁 淋2杜唐钟3

(1. 西南石油大学油气藏地质及开发工程国家重点实验室， 成都 610500；

2. 中石化西南油气分公司川东北采气厂, 四川 阆中 637400；3. 长庆油田第十采油厂, 甘肃 庆城 745100)

摘要：将岩心抽真空后加压饱和流体的过程视为外边界定压、内边界封闭的岩心内径向渗流，建立渗流模型和定解条件，首先将方程和定解条件无因次化，然后进行拉普拉斯变换，利用数值反演后编程得到无因次压力与无因次时间的关系曲线。根据无因次时间的定义，将岩心充分饱和状态的无因次时间变换为真实时间。实例计算结果表明，在较短的时间内，岩心就能达到完全饱和状态。

关键词：岩心； 抽真空； 加压饱和； 渗流模型； 饱和时间

在实验室测定相对渗透率曲线、岩石毛管压力曲线等试验中，需要对岩心抽真空后饱和某种流体，流体是否充分饱和岩心直接关系到后续实验的准确性。在实际实验准备中，对岩心加压饱和流体的时间，行业标准和相关实验书籍没有给出计算方法，实际操作中往往采取经验估计法。如果加压饱和时间不够，导致岩心没有被充分饱和，会造成后续实验的误差。本次研究提出了一种计算真空岩心加压饱和时间的方法，避免由于估计时间而造成的实验误差并提高实验效率。

1岩心内渗流物理过程

岩心在岩心筒内经真空泵抽真空，岩心初始状态时孔隙内压力为零，然后将配置好的地层水经加压泵泵注到岩心筒内，加到一定压力，模拟地层水渗流进入岩心。当岩心轴线的压力等于所施加的压力时，岩心被充分饱和，此时岩心内部压力处处相等[1]。岩心内部压力分布示意图如图1所示。

2渗流模型

加压饱和过程中，流体在岩心内为平面径向流。外边界定压，压力为ps；外边界为岩心半径rb；内边界封闭，内边界rc；初始状态岩心内部压力为真空，原始压力为真空pv。

图1　岩心内压力分布随时间变化示意图

渗流微分方程：

(1)

k—— 渗透率，10-3μm2；

μ —— 流体黏度，mPa·s；

φ —— 岩心孔隙度，无量纲；

t—— 时间，ks；

Ct—— 总压缩系数，MPa-1。

初始条件：

p(r,t=0)=pv

(2)

内边界条件：

(3)

式中：pv—— 真空压力，MPa；

rc—— 内边界半径，m。

外边界条件：

p(r=rb,t>o)=pb

(4)

式中：rb—— 外边界半径，m；

Pb—— 在岩心外边界上施加的压力。

3渗流模型求解

将上述定解问题无因次化[2]，得到：

(5)

初始条件：

pD(rD,tD=0)=0

(6)

内边界条件：

(7)

外边界条件：

pD(rD=rbD,tD>0)=1

(8)

无因次变量分别定义为：

(9)

(10)

(11)

(12)

然后对上述方程进行拉普拉斯变换[3]。

设函数f(t)，当t≥0时，在s的某一区域内收敛(其中s=σ+iω是复参量)，则由此确定函数f(t)的拉普拉斯变换为：

(14)

将上述无因次定解问题进行拉普拉斯变换，有：

(15)

初始条件：

(16)

内边界条件：

(17)

外边界条件：

(18)

方程(15)的通解是零阶虚宗量的Bessel函数I0和K0的线性组合，即：

(19)

由外边界条件得出：

(20)

由内边界条件得出：

(21)

根据式 (20)、(21)，可以求得：

(22)

(23)

将A、B带入式(19)，有

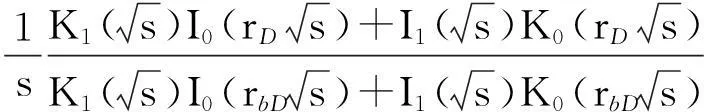
(24)

当rD=1时，

(25)

利用Stehfest数值反演[4-5]的方法可得到真实空间下压力随时间变化的曲线。Stehfest数值反演方法公式如下:

(26)

利用MATLAB编程计算无因次压力随无因次时间的关系图。

图2　无因次压力随无因次时间变化曲线

4实例计算

某致密气藏岩心直径为2.5 cm，长度为7.8 cm，孔隙度为13.6%，渗透率为0.013 4×10-3μm2，饱和液体黏度为1.2 mPa·s，综合压缩系数为5.6×10-4MPa-1。

在加压饱和真空岩心过程中，实际rc=0，但是在计算过程中，可以用一个相当小的数值代替。经验证，rc在足够小时对计算结果没有影响。本次取rc为1×10-6m。在实验室对岩心抽真空后，岩心并没有达到真正的真空状态，岩心中实际还存留有少量气体。在加压饱和过程中，实际是气水两相渗流，因此水的相渗透率不能采用岩石的绝对渗透率，为方便计算，取水的相对渗透率为0.1。

根据无因次时间变量的定义，将岩心充分饱和状态的无因次时间变换为真实时间。计算岩心完全饱和时间为136 s，时间较短。

5结语

(1)将真空岩心加压饱和流体过程视为流体在外边界定压、内边界封闭的岩心内径向渗流，建立渗流模型和定解条件。

(2)加压饱和时间与岩心渗透率成反比，与孔隙度、总压缩系数、流体黏度成正比。计算结果表明岩心加压饱和地层水在较短的时间内就能达到完全饱和。

参考文献

[1] 李晓平.地下油气渗流力学[M].北京:石油工业出版社，2008:96-99.

[2] 李晓平,张烈辉,刘启国.试井分析方法[M].北京:石油工业出版社，2009:35-36.

[3] 吴小庆.数学物理方程及其应用[M].北京:科学出版社，2008:122-126.

[4] STEHFEST H. Algorithm 368 Numerical Inversion of Laplace Transforms[J]. Communications of ACM, 1970,13(1):47-49.

[5] STEHFEST H. Remark on Algorithm 368 Numerical Inversion of Laplace Transforms[J]. Communications of ACM, 1970,13(10):624-625.

Method to Calculate the Core Pressurized SaturationTime of Formation Water

SUGuangle1LIXiaoping1YUANLin2DUTangzhong3

(1. State Key Lab of Oil & Gas Reservoir Geology and Exploitation, Southwest Petroleum University,Chengdu 610500, China; 2. Northeastern Sichuan Production Gas Plant of Sinopec Southwest Oil and Gas Field Co., Langzhong Sichuan 637400, China;3. The Tenth Oil Production Plant of Changqing Oilfield Company, Qingcheng Gansu 745100, China)

Abstract:This paper will consider the process of saturating core with liquid as a radial flow in core with a constant pressure outer boundary and closed inner boundary. After the differential equation and boundary conditions is established, we can rewrite them in dimensionless form, then in Laplasse transform. Finally, by numerical inversion method we could get the curve of dimensionless pressure and dimensionless time. According to the definition of the dimensionless time, the dimensionless time when the core was fully saturated is converted into the real time. The example shows the core is completely saturated in a relatively short time.

Key words:core; evacuation; pressurized saturation; percolation model; saturation time

文献标识码：A

文章编号：1673-1980(2016)01-0034-03

中图分类号：TE312

作者简介：苏广乐(1984 — )，男，河南漯河人，西南石油大学在读硕士研究生，研究方向为油气藏工程。

基金项目：国家杰出青年科学基金项目“油气渗流力学”(51125019)

收稿日期：2015-03-22