基于自适应变异因子策略的混合蛙跳算法

赵付青,陈自豪

(1.兰州理工大学 计算机与通信学院,甘肃 兰州　730050;

2.西北工业大学 现代设计与集制造技术教育部重点实验室,陕西 西安　710072)



基于自适应变异因子策略的混合蛙跳算法

赵付青1,2,陈自豪1

(1.兰州理工大学 计算机与通信学院,甘肃 兰州730050;

2.西北工业大学 现代设计与集制造技术教育部重点实验室,陕西 西安710072)

摘要由于基本混合蛙跳算法在对问题的优化求解中存在着收敛速度慢、优化精度低且容易陷入局部最优等问题,因此提出了一种新的混合蛙跳算法。对基本混合蛙跳算法的组内更新策略进行重新设计,引入自适应变异因子来控制青蛙的移动步长；在算法中将改进的粒子群优化算法有机地嵌入其中,这样算法在搜索过程中就增加了发现新解的概率,维持了种群的多样性,从而使算法不易陷入局部最优。通过对标准函数进行优化测试,结果证明其具有良好的优化性能。

关键词混合蛙跳算法；自适应变异因子；移动步长；粒子群优化算法

混合蛙跳算法(SFLA,shuffled frog leaping algorithm)是2003年由Eusuff和Lansey提出的一种基于群体智能的生物进化算法[1]。它具有参数少、概念简单、计算速度快、全局寻优能力强及易于实现等特点。目前该算法在改进和应用方面都得到了相应提高,并且利用它解决了许多实际优化问题,如函数优化、水资源网络分配问题、成品油管网优化设计、车间调度问题、旅行商问题等[2-4]。然而它还是存在着许多缺点,如收敛速度较慢、优化精度相对低、易陷入局部最优等,尤其在解决高维函数问题时,这些缺点表现的更明显,从而算法的效率非常低。因此改进基本混合蛙跳算法,提高算法性能就变得非常急切。目前,研究者们用不同的方法对算法的各个过程进行改进。文献[5-10]中介绍了国内和国外学者们对基本混合算法进行的改进,确实提高了算法的优化性能。但是现有的混合蛙跳算法的优化性能依旧比较低,所以需要对其进行进一步的改进和研究。

我们重新设计了混合蛙跳算法的组内更新策略,引入自适应变异因子来动态控制青蛙移动步长,并将粒子群优化算法有机地嵌入其中,从而增加算法发现新解的概率,提高了解的多样性,避免算法陷入局部最优,提高了算法的优化性能。

1混合蛙跳算法

1.1算法描述

SFLA是一种新型的后启发式群体智能进化算法。它的实现机理是通过模拟现实自然环境中青蛙群体在觅食过程中所体现的信息交互和协同合作行为,来完成对问题的求解过程。采用模因分组方法把种群分成若干个子种群,每个子种群称为模因分组,种群中青蛙被定义为问题解。模因组中的每个青蛙都有努力靠近目标的想法,具有对食物源远近的判断能力,并随着模因分组的进化而进化。在模因组的每一次进化过程中,找到组内位置最差和最好的青蛙。组内最差青蛙要按照一定更新策略来进行位置调整。对每个模因组进行一定次数的模因进化后,把所有模因分组重新混合成新的群体,实现各个模因组交流与共享彼此间的信息,算法一直执行到种群预定的进化次数才结束。

SFLA中信息传递是通过种群分类来实现的,它相间进行局部进化和重新混合过程,有效地将全局信息交互和局部搜索相结合,具有很强的全局搜索能力。

1.2算法数学模型

混合蛙跳算法首先随机初始化P个解来组成青蛙的初始种群,例如解决d维的优化问题时,可以把第i个解记作Xi=(xi1,xi2,…,xid),适应度值可记作Y=f(Xi),Y是目标函数值。根据适应度将P只青蛙按从大到小排列,然后对种群进行分组,把它分为n个模因组,每组有s个青蛙(解)。把第一只青蛙分配到第一个模因组,第二只青蛙分配到第二个模因组,直到第n只青蛙分配到第n个模因组；接着把第n+1只青蛙分配到第1个模因组,第n+2只青蛙分配到第2个模因组,依次类推,直到所有解分配完毕。模因组中最差青蛙记为Xw,最好青蛙记为Xb,整个种群中位置最好的青蛙则记为Xg,其中Xb=(xb1,xb2,…,xbd),Xw=(xw1,xw2,…,xwd),Xg=(xg1,xg2,…,xgd)。在模因组中执行局部搜索,适应度值最差的青蛙得到更新,其公式如下:

ΔX=rand()×(Xb-Xw),

(1)

newXw=Xw+ΔX,ΔXmax≥ΔX≥-ΔXmax

(2)

其中:newXw为最差解Xw更新后的新解,newXw=(newxw1,newxw2,…,newxwd);ΔX为青蛙的最大移动步长;rand()表示0～1之间的随机数。计算新解,如果得到了更优的解,则用newxw取代Xw,否则则用Xg代替式(1)中的Xb,重新计算新解。如果产生新解的适应度值还没被改善,那么就随机生成新解。重复执行以上更新过程对模因组进行模因进化,当达到设定的迭代次数后模因进化结束,重新混合所有模因组成新的种群,再对新种群按照上面分配原则重新划分模因组,然后继续对每个模因组进行模因进化。如此反复,直到满足终止条件。

1.3算法流程

步骤1随机生成包含P个解的初始种群P=N×S,青蛙的最大移动步长设为ΔXmax,子种群间最大混合迭代次数设为G,子种群内迭代次数设为T;

步骤2计算种群中每个解的适应度值,并用Xg表示全局最优解；

步骤3按照适应度值对种群中P个解进行降序排列,然后把种群划分为N个子种群,每个子种群体中含有S个解;

步骤4根据适应度值找到每个子种群中的最差解和最优解,将它们分别记作Xw和Xb,以及当前种群的最优解Xg,利用更新策略,对子种群的最差解Xw进行更新;

步骤5判断是否达到子群内的最大迭代次数,如果没有就转到步骤4,否则重新混合所有子种群,构造下一代种群;

步骤6判断终止条件。群间迭代如果达到终止条件就结束,算法结束并输出最优解Xg;否则转向步骤2。

2改进的混合蛙跳算法

2.1引入自适应变异因子

引入自适应变异因子主要是对青蛙的移动步长进行动态调整。因为在算法进化的初期阶段应加大移动步长,扩大搜索范围,使青蛙快速向更好的方向跳动,从而加快算法的收敛速度。但是在进化的后期应该减小青蛙的移动步长,缩小搜寻空间,让算法进行深度局部搜索,避免跳出最好解。同时组内青蛙的平均值比最优青蛙更能代表组内青蛙所处的位置,因此用组内平均值代替最优解来对最差解进行更新。在基本算法中更新最差解时,最差青蛙的移动起点总是从自身出发,这样产生的解还保留了最差青蛙部分坏的信息,容易产生一些劣质解,影响算法的收敛速度。文献[10]中提到了青蛙个体对自己的历史最优解存在记忆功能,因此采用以从组内最优青蛙和最差青蛙的历史最优解之间的随机点出发和从自身出发的随机混合方式来更新最差青蛙,这样不仅能提高解的质量,而且还增加种群多样性。具体的更新策略为

(3)

其中:Δx代表青蛙的移动步长;Δxmax是Δx的最大值;r1、r2和r3是0~1之间的随机数;Xa代表青蛙组内的平均值;Xw和 Xb分别是组内的最优和最差解;Xh是最差青蛙的历史最优值;K是自适应变异算子,它的值是随着进化的过程呈线性递减的;Ke和Ks分别是K取值的最小值和最大值。

2.2嵌入粒子群优化算法

粒子群优化(PSO,particleswarmoptimization)算法是一种有效的全局寻优算法,目前它已经被广泛应用于数值的优化、神经网络训练、数据挖掘等应用领域。在PSO中,可以用三元组(Xi,Vi,Pi)来表示i粒子,其中Xi=(xi1,xi2,…,xid)T为其目前位置;Vi=(vi1,vi2,…,vid)T为其目前速度;Pi=(pi1,pi2,…,pid)T为其经过的最优位置；又设全局最优位置Pg=(pg1,pg2,…,pgd)T∈S ,则i粒子的速度进化公式为

vij(t+1)=wvij(t)+c1r1(pij(t)-xij(t))+

c2r2(pgj(t)-xij(t)),

1≤i≤s,1≤j≤d

(4)

其中:r1,r2表示(0,1)之间的随机生成数,w代表惯性权重;c1与c2代表加速正常数。文献[9]中提出了一种带有递减扰动项的改进粒子群算法(DDPSO),由于SFLA和DDPSO在搜索机制方面具有各自的优点,把它们相结合可以提高算法搜索新解的能力,同时也扩大算法的搜索空间,使其不易陷入局部最优。改进混合蛙跳算法表述如下:

初始化种群及参数:种群大小为P,子种群个数为S ,子种群内最大迭代次数为N,种群间混合迭代次数为 G。

Fori=1∶G

If mod(I,R)~=0

用组内更新策略改进的SFLA进行搜索

Else

用DDPSO算法进行搜索

End

End

其中R为算法交替的控制参数,mod( )代表取余函数,SFLA和DDPSO相结合维持了种群的多样性,提高了整个算法的性能。

3实验方法与结果分析

3.1实验设计

为验证改进SFLA的优化性能,采用如表1所列的Sphere,Rosenbrock,Rastrigin,Griewank,Ackley和Schaffer’s f6等标准测试函数对SFLA和ISFLA进行仿真实验比较。实验代码用MATLAB实现,电脑用个人PC机,操作系统是Windows 7,CPU为Core i3,内存是2 G。6个标准测试函数的3D图见图1。

参数设置:P=300,N=10,S=30,T=20,G=500,TS=8,Te=4,R=10,其他需要的参数配置和文献[9]中一致。基本SFLA和改进SFLA两个算法的相关参数相同,它们分别对6个测试函数独立运行30次。

3.2实验结果与分析

改进SFLA和基本SFLA的实验对比结果见表2。从表2的实验结果可以明显看出,ISFLA的优化结果要比SFLA的好,而且ISFLA 的标准差要小于SFLA,表明ISFLA的稳定性也要好于SFLA。ISFLA采用自适应变异因子,动态地控制青蛙移动步长,从而平衡了算法的开发与探索,提高了其收敛速度；同时把SFLA和DDPSO相结合,利用它们各自的寻优特性,增强了整个算法的优化性能。ISFLA不容易陷入局部最优,有很强的全局寻优能力,而且其鲁棒性很强。

表1　6个标准测试函数

图1　6个标准测试函数的3D图Fig.1　3D diagram of six standard test functions

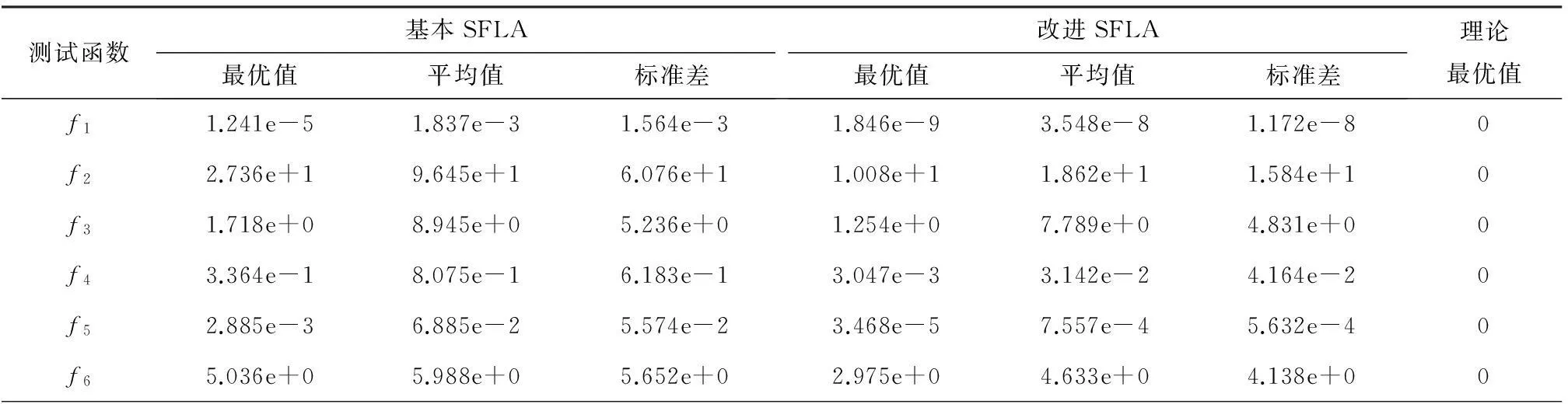
测试函数基本SFLA最优值平均值标准差改进SFLA最优值平均值标准差理论最优值f11.241e-51.837e-31.564e-31.846e-93.548e-81.172e-80f22.736e+19.645e+16.076e+11.008e+11.862e+11.584e+10f31.718e+08.945e+05.236e+01.254e+07.789e+04.831e+00f43.364e-18.075e-16.183e-13.047e-33.142e-24.164e-20f52.885e-36.885e-25.574e-23.468e-57.557e-45.632e-40f65.036e+05.988e+05.652e+02.975e+04.633e+04.138e+00

为了验证改进SFLA的收敛性能,上述6个测试函数采用两种算法运行30次后求得的平均适应度进化曲线见图2,图2中迭代进化代数G由横坐标表示,每一代的平均最优适应值由纵坐标表示。

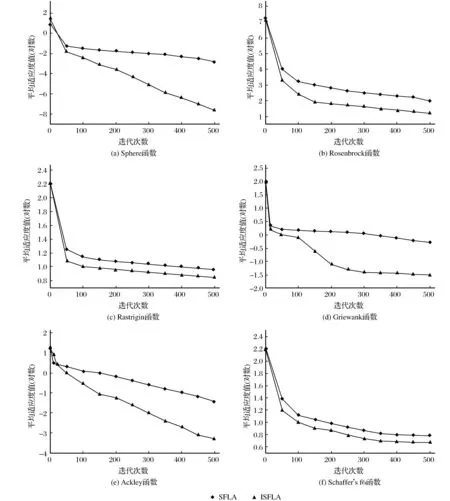
图2　6个标准测试函数的平均进化曲线Fig.2　The average evolutionary curve of six standard test functions

从图2可以明显看出,ISFLA的收敛速度比基本 SFLA的快,在算法进化初始阶段就能快速收敛到理论最优解附近,然后向理论最优解不断地靠近,收敛性能非常好。比较算法对被测函数的求解精度,表3列出了它们的目标收敛精度,维数设置为30,对ISFLA算法独立运行30次,实验结果由表4所列。

通过表4中的结果可以得知,在指定的目标收敛精度下对以上6个标准测试函数进行优化,ISFLA的成功率很高,一般都能达到 90%以上,而SFLA算法的成功率相对比较低,大部分都很难达到指定的精度,因此可以说明ISFLA算法在求解优化问题中有较高的成功率。

表3　6个测试函数的目标收敛精度

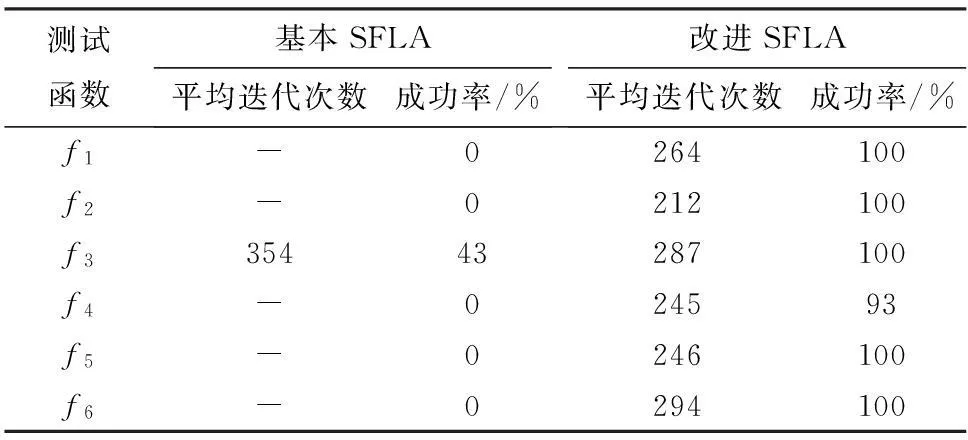
表4　改进SFLA和基本SFLA的平均迭代次数对比

综上所述,我们提出的改进算法克服了基本混合蛙跳算法的一些缺点,提高了算法的收敛速度和寻优精度,同时算法也不易陷入局部最优,提高了算法的优化性能。

4结论

在基本混合蛙跳算法的基础上,在其组内更新策略中引入自适应变异因子,对青蛙的移动步长进行有效地动态调整。在对最差解更新策略中采用以从最优解和最差解的历史最优值之间随机点出发和从自身出发混合进行的模式,提高了解的质量,从而加快了算法的收敛速度。在全局信息交换过程中将粒子群优化算法有机地嵌入其中,增加了在搜索过程中发现新解的概率,提高了解的多样性,使算法不易陷入局部最优。最后通过仿真实验表明改进算法的性能更好,今后要对改进算法在实际应用方面进行研究。

参考文献:

[1]Eusuff M M,Lansey K E.Optimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm[J].Journal of Water Resources Planning and Management,2003,129(3):210-225.

[2]Poli R,Kennedy J,Blackwell T.Particle Swarm Optimization[J].Swarm Intelligence,2007,1(1):33-57.

[3]Niknam T,Farsani E A,Nayeripour M,etal.A New Tribe Modified Shuffled Frog Leaping Algorithm For Multi-objective Distribution Feeder Reconfiguration Considering Distributed Generator Units[J].European Transactions on Electrical Power,2012,22(3):308-333.

[4]Amiri B,Fathian M,Maroosi A.Application of Shuffled Frog Leaping Algorithm on Clustering[J].International Journal of Advanced Manufacturing Technology,2009,45(1-2):199-209.

[5]Elbeltagi E,Hegazy T,Grierson D.A Modified Shuffled Frog-leaping Optimization Algorith-m:Applications to Project Management[J].Structure and Infrastructure Engineering,2007,3(1):53-60.

[6]Khorsandi A,Alimardani A,Vahidi B,etal.Hybrid Shuffled Frog Leaping Algorithm and Nelder-Mead Simplex Search for Optimal Reactive Power Dispatch[J].IET Generation,Transmission & Distribution,2011,5(2):249-256.

[7]Roy P,Chakrabarti A.Modified Shuffled Frog Leaping Algorithm for Solving Economic Load Dispatch Problem[J].Energy and Power Engineering,2011,3(4):551.

[8]Rahimi-Vahed A,Mirzaei A H.Solving a Bi-criteria Permutation Flow-shop Problem Using Shuffled Frog-leaping Algorithm[J].Soft Computing,2008,12(5):435-452.

[9]赵付青,唐建新,张秋余.一种带有递减扰动项的粒子群优化算法[J].兰州理工大学学报,2011,37(6):88-93.

[10]代永强,王联国.带记忆功能的混合蛙跳算法[J].计算机工程与设计,2011,32(9):3 170-3 173,3 202.

Shuffled Frog-Leaping Algorithm Based on the Theory of Adaptive Mutation Factors

Zhao Fuqing1,2,Chen Zihao1

(1.SchoolofComputerandCommunication,LanzhouUniversityofTechonlogy,Lanzhou730050,China;2.KeyLaboratoryofContemporaryDesign,IntegratedManufacturingTechnology,MinistryofEducation,NorthwesternPolyTechnicalUniversity,Xi’an710072,China)

AbstractShuffled frog-leaping algorithm is an optimized solution,but its local search ability is weak,optimization accuracy is low and it is easily caught in local optimum.In this paper,a modified SFLA is proposed to overcome the disadvantages.This new algorithm reconstructs the initial SFLA by redesigning its update strategy within the group and using adaptive mutation factors to control frogs' step length.This new algorithm contains the improved particle swarm optimization as an integrated part which increases the chances of finding new solutions in the process of searching,maintains population diversity and avoids being trapped in local optimum.And an optimization test on criteria functions proved a good optimal performance of SFLA.

Key wordsShuffled frog-leaping algorithm;Adaptive mutation factors;Step length;Particle swarm optimization

中图分类号:TP391

文献标志码:A

文章编号:1004-0366(2016)01-0006-06

作者简介:赵付青(1977-),男,甘肃酒泉人,博士,教授,研究方向为复杂系统、计算智能.E-mail:7673385510@qq.com.

基金项目:国家自然科学基金(51365030).

收稿日期:2015-03-31;修回日期:2015-05-06.

doi:10.16468/j.cnki.issn1004-0366.2016.01.002.

引用格式:Zhao Fuqing,Chen Zihao.Shuffled Frog-Leaping Algorithm Based on the Theory of Adaptive Mutation Factors[J].Journal of Gansu Sciences,2016,28(1):6-11.[赵付青,陈自豪.基于自适应变异因子策略的混合蛙跳算法[J].甘肃科学学报,2016,28(1):6-11.]