波形特征和频谱特征组合识别纤维断裂声信号

赵春龙， 于伟东， 刘洪玲

(东华大学 纺织学院， 上海 201620)

波形特征和频谱特征组合识别纤维断裂声信号

赵春龙， 于伟东， 刘洪玲

(东华大学 纺织学院， 上海 201620)

利用波形特征和频谱特征组合的方法，去除背景噪声和瞬态噪声对纤维断裂声信号判识的影响，实现对纤维断裂声信号的准确识别.首先,采用小波包法去除部分背景噪声，然后利用其波形和频谱特征去除声信号中的剩余噪声.试验结果证明，该方法的误差率小于4%，可以有效应用于纤维断裂伸长率的表征.

纤维断裂声信号； 小波包去噪； 频谱特征； 波形特征； 断裂伸长率分布

纤维的断裂伸长率分布是衡量纤维拉伸性能均匀性的一个重要指标[1]，其直接关系到成纱的加工和纺织品的最终适用性能.利用束纤维与单纤维拉伸测量结果间的关系[2-3]，通过束纤维的拉伸曲线可以预测单纤维的断裂伸长率分布[4-5]，避免繁琐、冗长的单根纤维的测量.基于声与拉伸曲线的组合，采用振幅阈值去噪方法区分底噪声和环境噪声，从而计算得到刚性纤维的断裂伸长率分布[6-8]已见报道.但对于羊毛类有卷曲或交叉排列的纤维束而言，因其在拉伸中存在交互作用而产生瞬态噪声信号，导致断裂与否判断的失误[9].因此，将此类瞬态噪声信号剔除并准确判定纤维断裂声信号是问题的关键.

已有研究采用小波去噪对原始束纤维断裂声信号进行去噪处理，然后将去噪后的信号中疑似纤维断裂声信号提取出来，并采用复合波形参数的方法对纤维断裂声信号进行辨别[9].该方法对于断裂声信号幅值较大的澳毛纤维有用，对于断裂声信号幅值较小的国产羊毛纤维则效果较差[10].为此，本文针对断裂声信号幅值较小而瞬态噪声较强、较多的羊毛纤维，利用纤维断裂声信号在波形和频率上的特征，采用波形特征和频谱特征组合方法，将其与背景噪声和瞬态噪声区分开来，从而实现对纤维断裂声信号的识别.

1 试 验

1.1 试样

所有试样均为国产羊毛纤维，含有较多的天然卷曲.试验条件为标准大气条件.

1.2 测量仪器与方法

测量仪器为自行研制的智能束纤维强力仪(TMT-InFiBTensor)，该仪器拉伸时拉伸速率恒定为6.6 mm/min，初始拉伸夹头间隔距为10 mm.

录取声信号的麦克风为AT9904，其频率响应范围为30～18 000 Hz，灵敏度为-42 dB，测量时其位于试样正上方5 mm处.录取声信号所用的软件为cooledit，用该软件录取声信号时采样频率为40 kHz，声道为单声道，采样精度为16 bit.声信号的录取先于束纤维的拉伸，当开始拉伸束纤维时，束纤维强力仪会同时发出一个声音信号，作为拉伸开始的标志.

1.3 噪声去除原理

在束纤维拉伸过程中，可采集得到的声信号包含3部分：纤维断裂声信号、背景噪声，以及由于纤维间纠缠、摩擦、滑移、脱开等造成的瞬态噪声.羊毛纤维束拉伸时的声信号如图1所示.其中，图1(b)是图1(a)方框中信号的放大显示；图1(c)和1(d)为对称和非对称两种不同类型的瞬态噪声.

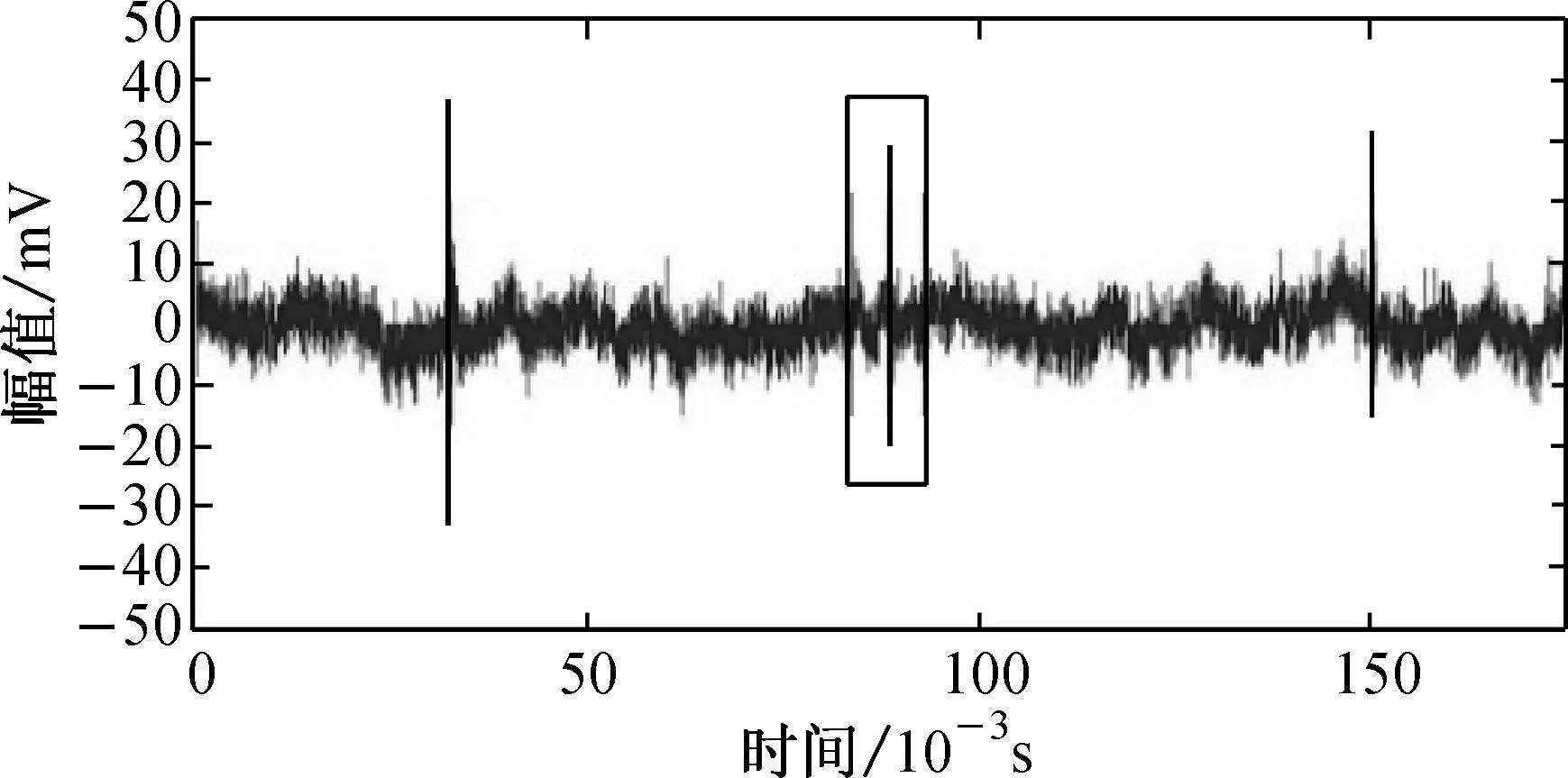
(a) 带背景噪声的声信号

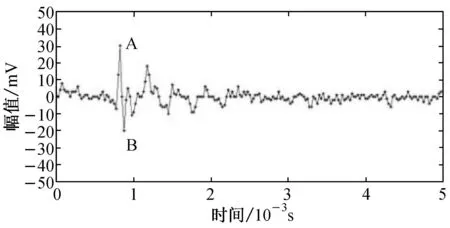
(b) 纤维断裂的声信号

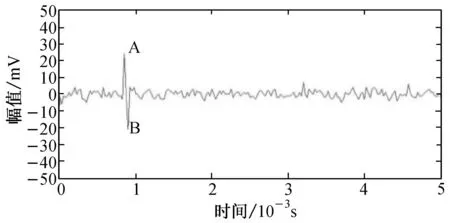
(c) 瞬态噪声一

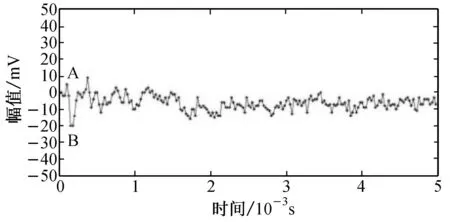
(d) 瞬态噪声二

从图1可以发现，纤维断裂声信号振幅明显大于背景噪声，因而可以利用正振幅(图1(b)中A点值)与负振幅(图1(b)中B点值)的幅值差大于背景噪声中任意两个信号点的幅值差，将纤维断裂声信号提取出来.但瞬态噪声的正负振幅幅值差有时会与纤维断裂声信号幅值差相近甚至更大，如图1(c)和1(d)所示的两种类型的瞬态噪声，均无法以幅值差阈值来识别提取. 对比图1(c)和1(d)可以发现，前者中A点振幅值与B点振幅值相近，为对称振幅，而后者为非对称幅值，故可以通过该差异去除图1(d)型的非对称瞬态噪声. 对比图1(b)和1(c)可以发现，两者在对称性和正负振幅幅值差上差别均较小，但后者无余震迹象，故可以通过此差异将其区别除去.

2 结果与讨论

2.1 小波去噪结果

小波去噪可以同时在时频域中对信号进行分析[11]，为了显示出小波去噪的效果，取时间间隔为2 s的原信号作说明. 原信号如图2(a)所示，小波去噪后的信号如图2(b)所示.其中，小波去噪方法如下：(1)参照文献 [9]采用db5 小波[12]对原始信号进行6层分解；(2)对高频6层信号重构并相加生成新的信号[14]；(3)对新生成的信号再次采用 db5 小波进行6层分解；(4)采用最小极大方差阈值对各层噪声分别进行软阈值[15]处理；(5)重构阈值处理过的各层信号[16]. 由图2可以观察到，小波去噪去除了背景噪声，降低了纤维断裂声信号的幅值，其中对振幅较小信号的降幅特别明显.

对于较弱的纤维断裂声信号，小波去噪不仅会降低其幅值，还会对波形产生破坏.正负振幅差在35 mV内的纤维断裂声信号如图3(a)所示，其小波去噪结果如图3(b)所示；正负振幅差在60 mV内的纤维断裂声信号如图3(c)所示，其小波去噪结果如图3(d)所示.

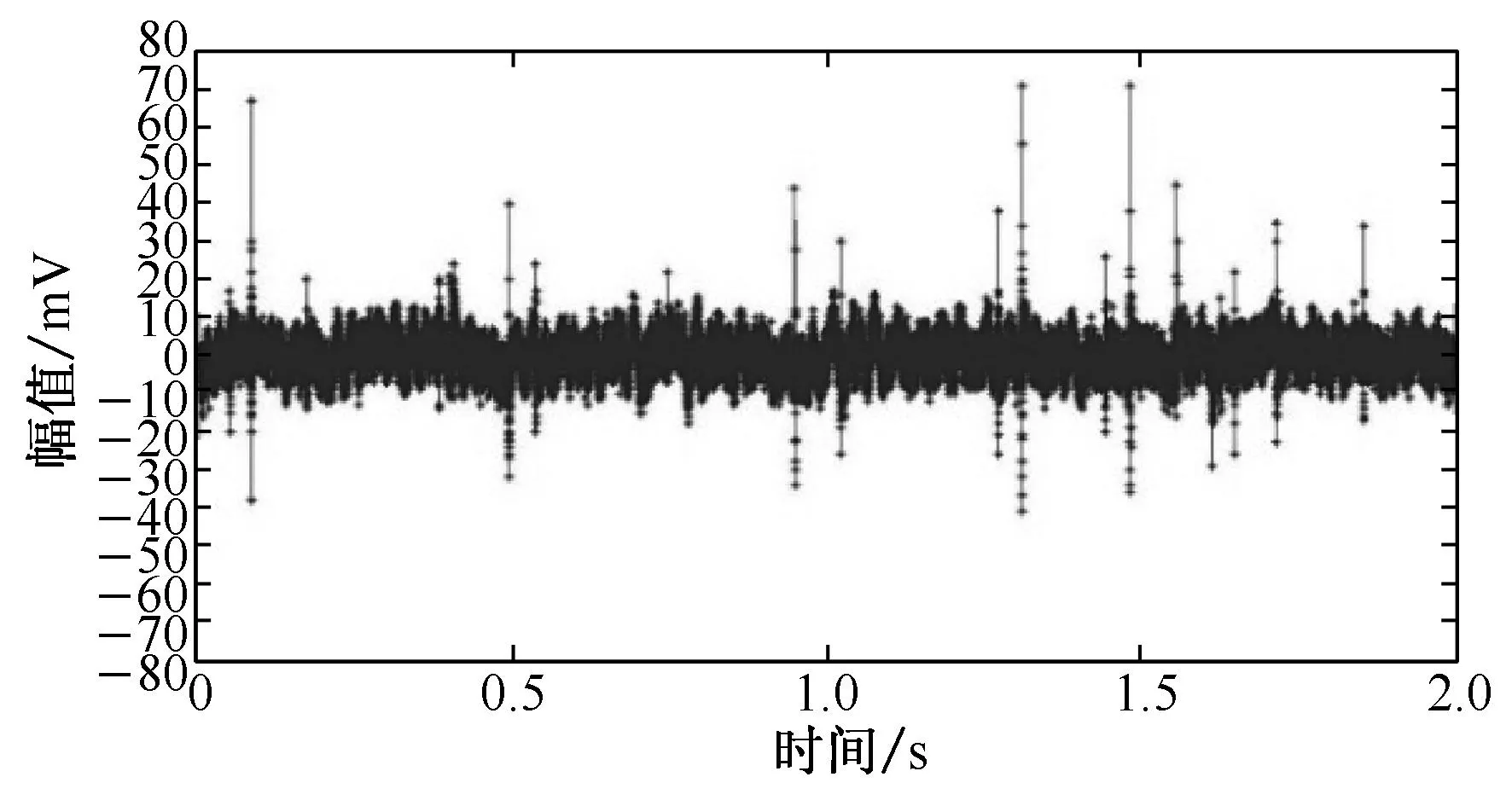
(a) 原始信号

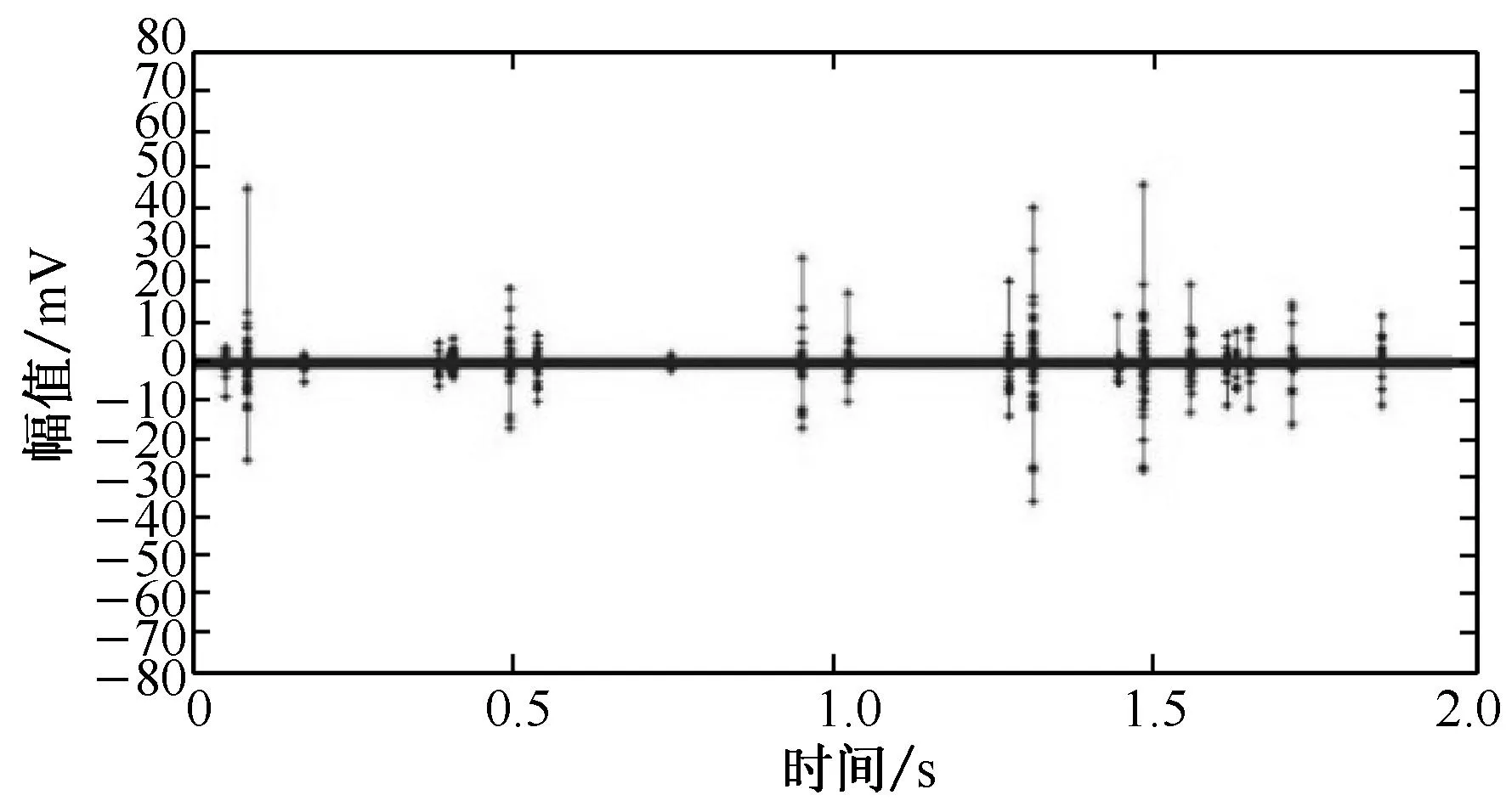
(b) 小波去噪后信号

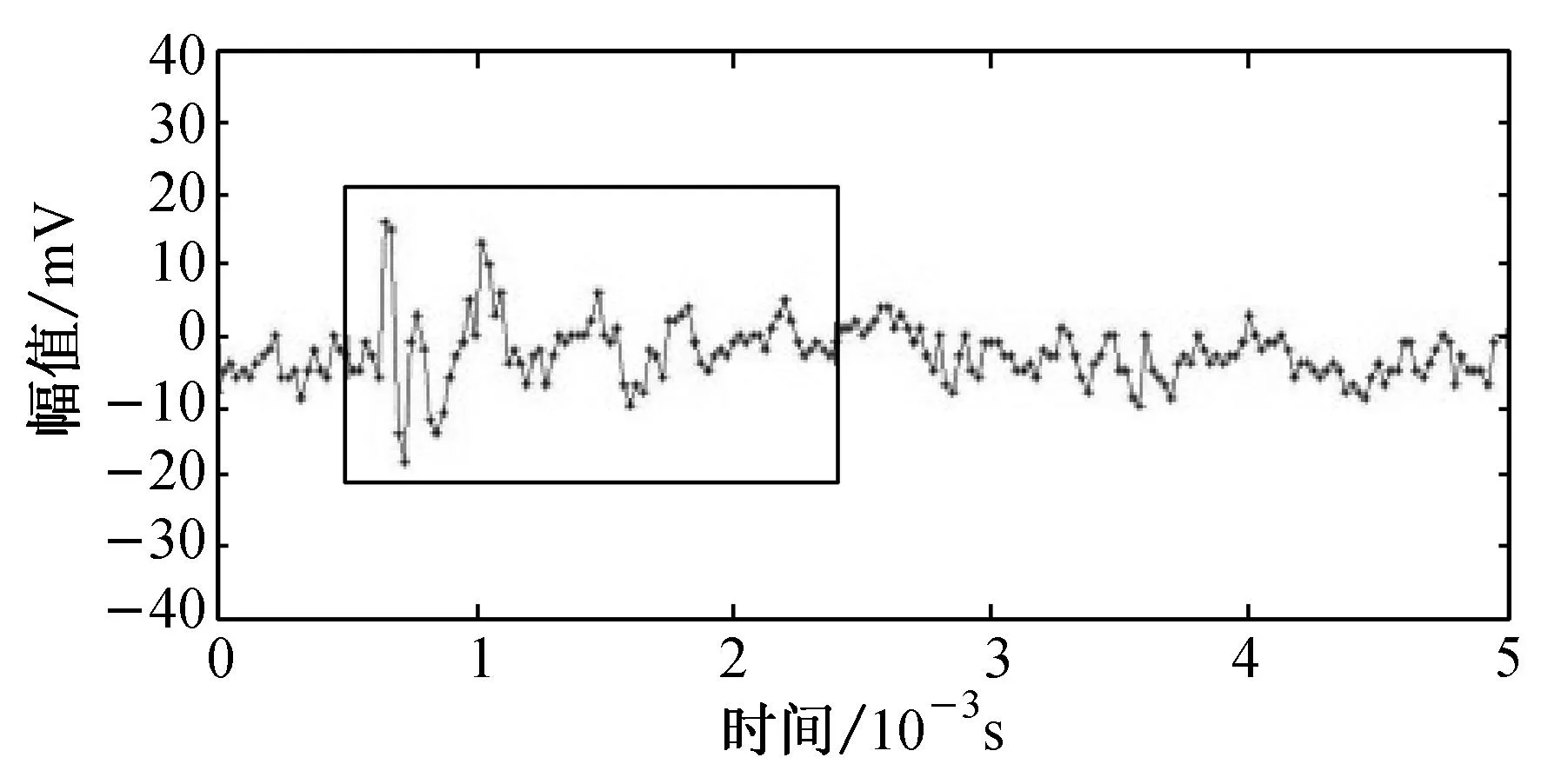
(a) 正负振幅差在35 mV内的信号

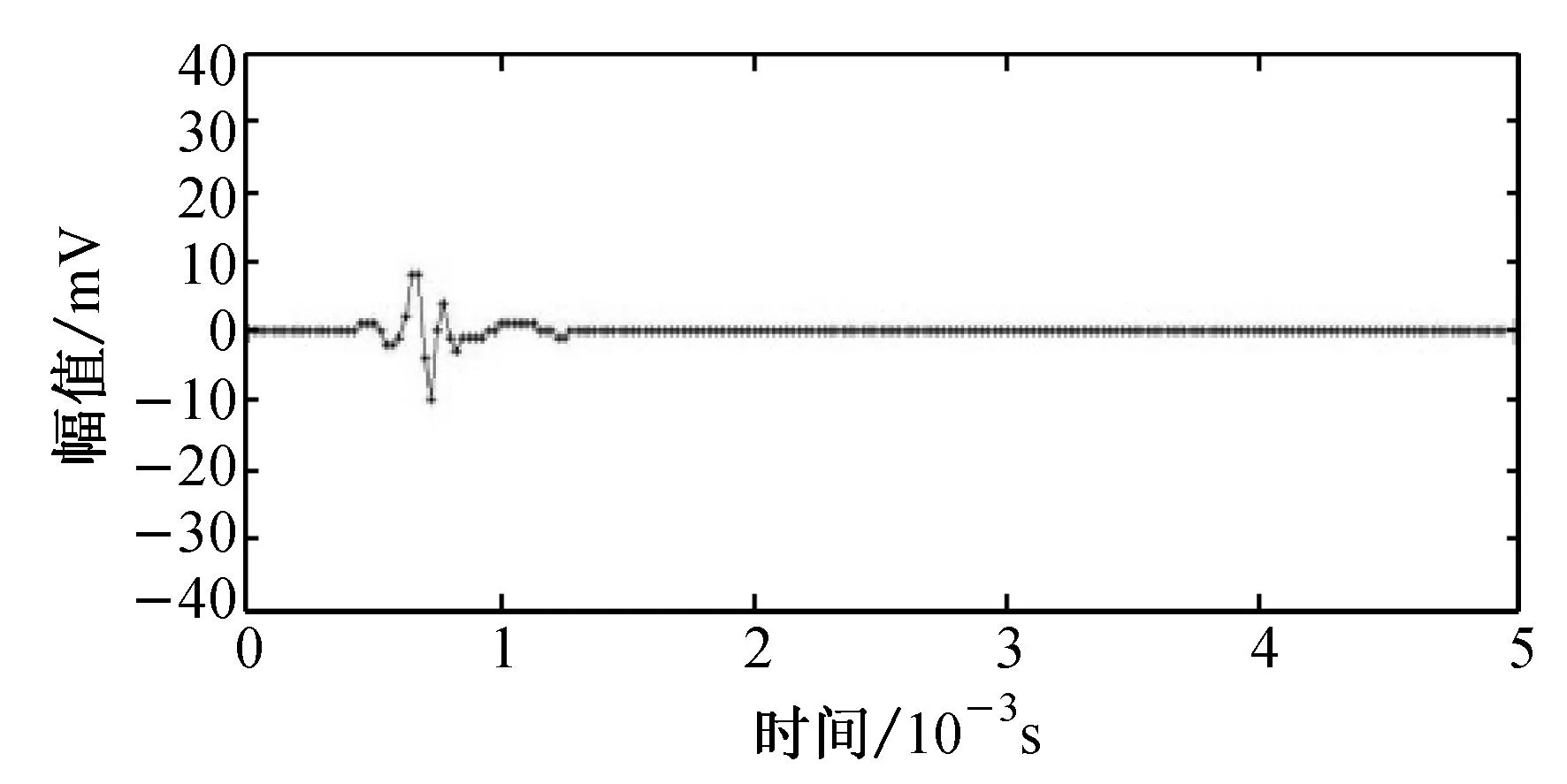
(b) 图(a)中的信号去噪后结果

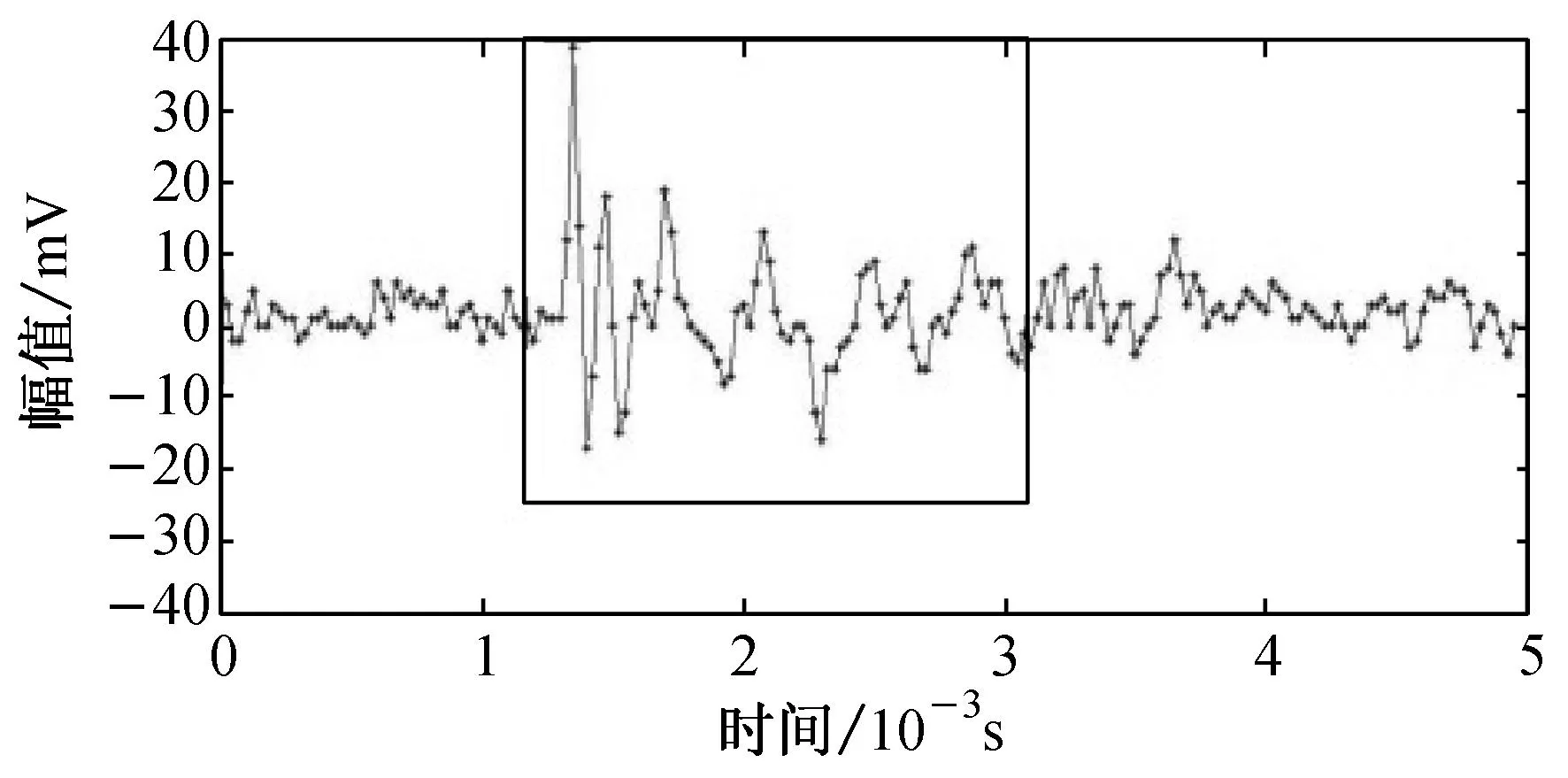
(c) 正负振幅差在60 mV内的信号

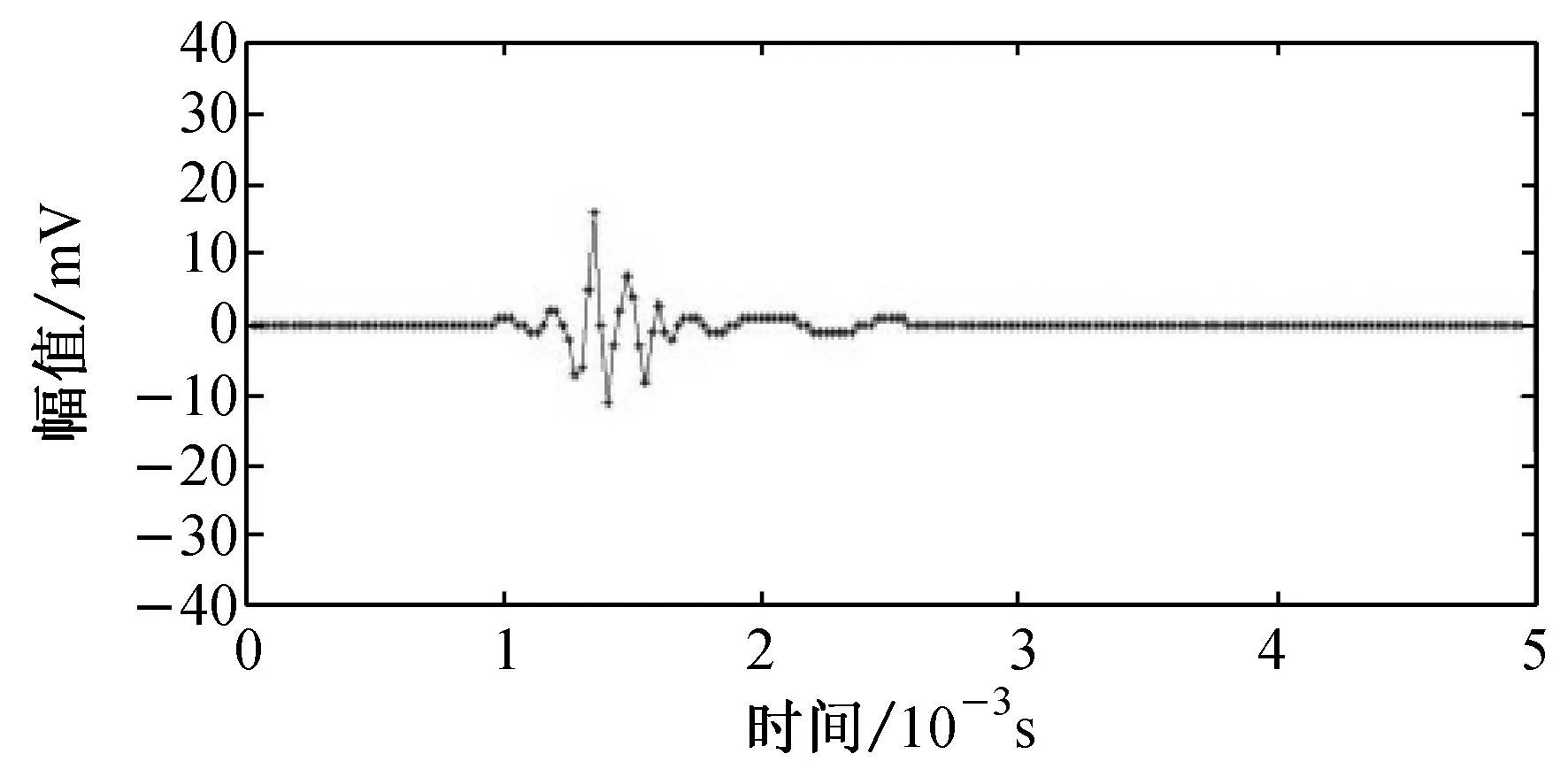
(d) 图(c)中的信号去噪后结果

从图3可以发现，小波去噪对幅值较小的纤维断裂声信号(占总纤维断裂根数的5%以上)的破坏非常明显，图3(a)和3(c)两纤维断裂声信号经过小波去噪后其幅度[9]分别下降了47.1%和50.0%，波形持续时间[9]分别下降46.3%和26.4%，波形衰减时间[9]分别下降50.0%和28.0%，声信号的能量[9]降低了78.3%和83.6%.在此基础上进行复合波形参数的计算必然存在较大误差.

2.2 小波包去噪结果

小波包去噪[17]是在小波多分辨分析基础上，将小波分解中获得的高频部分继续分解为低频和高频两部分，与小波多分辨分析相比，它具有更精细的去噪能力，小波分解和小波包3层分解分别如图4(a)和4(b)所示，其他多层分解依次类推. 小波包分解是将小波分解中获得的高频部分继续分解为低频和高频部分.

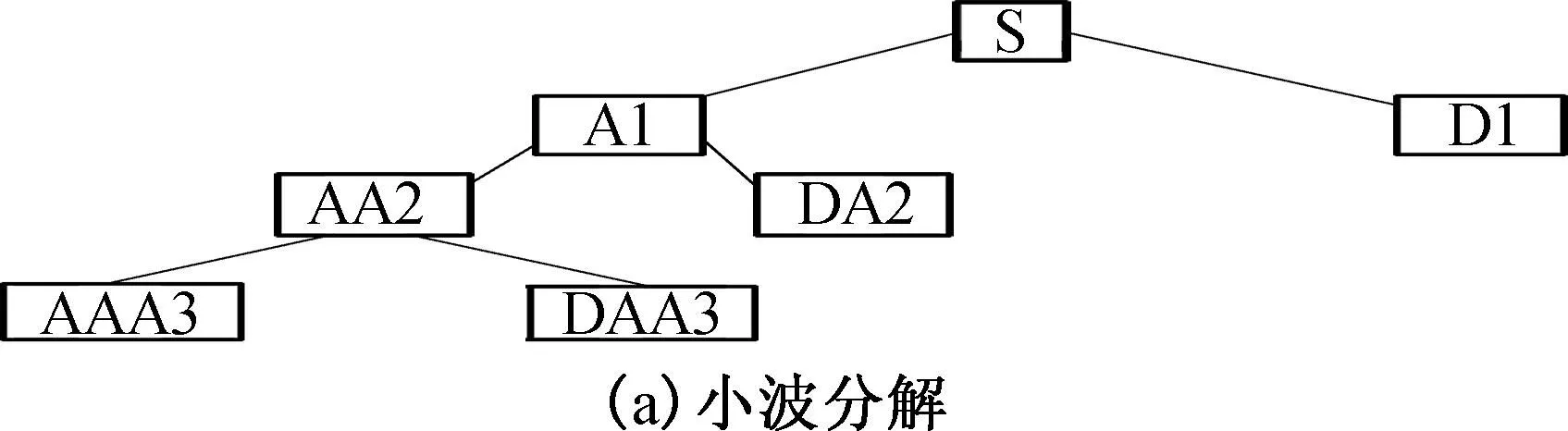
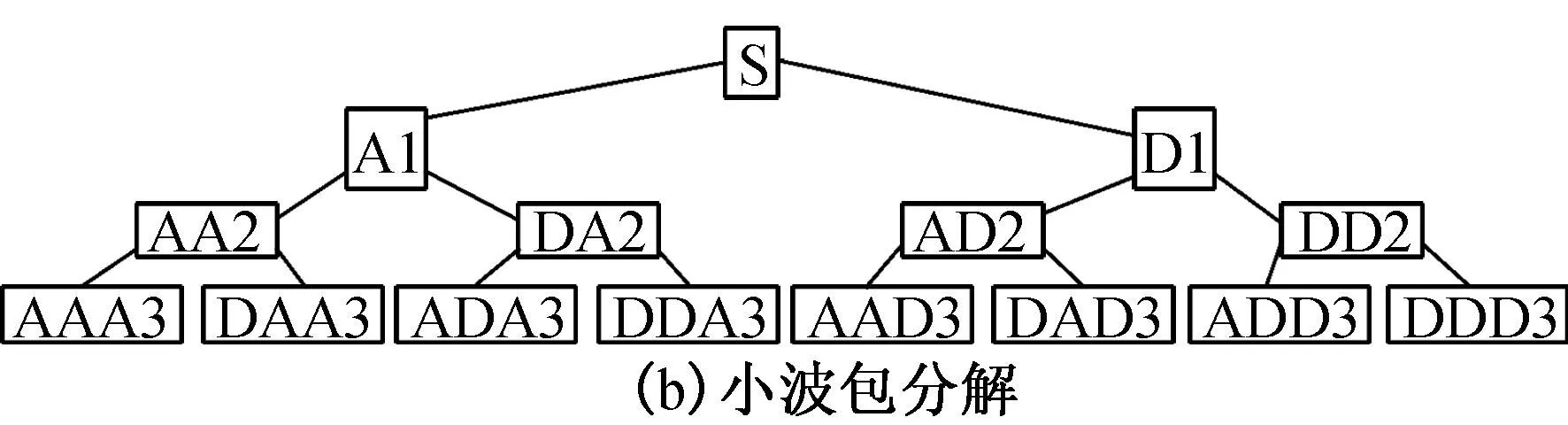
S—原始信号；A—低频信号；D—高频信号

在小波包分析中可以利用熵值判定低频或高频是否要继续分解，从而产生最优小波包分解[18].如果用小波包完全去除背景噪声，其去噪结果会与小波去噪相同，因而本文采用如下的去噪方法去除部分背景噪声，以有利于后面的频谱分析.(1)采用 db5 小波对原始信号进行5层最优小波包分解(由于采用5层分解就可以达到较好的效果，可使最前端的低频系数部分恰不含有纤维断裂声信号，因此采用5层分解)；(2)将不存在纤维断裂声信号频率范围的系数调整为0；(3)重构阈值处理过的各层信号，合并输出去噪信号[19-20].

取如图5(a)所示的2 s原信号，对其进行小波包去噪，得到去噪后的信号如图5(b)所示.正负振幅差在35 mV内的纤维断裂声信号如图5(c)所示，

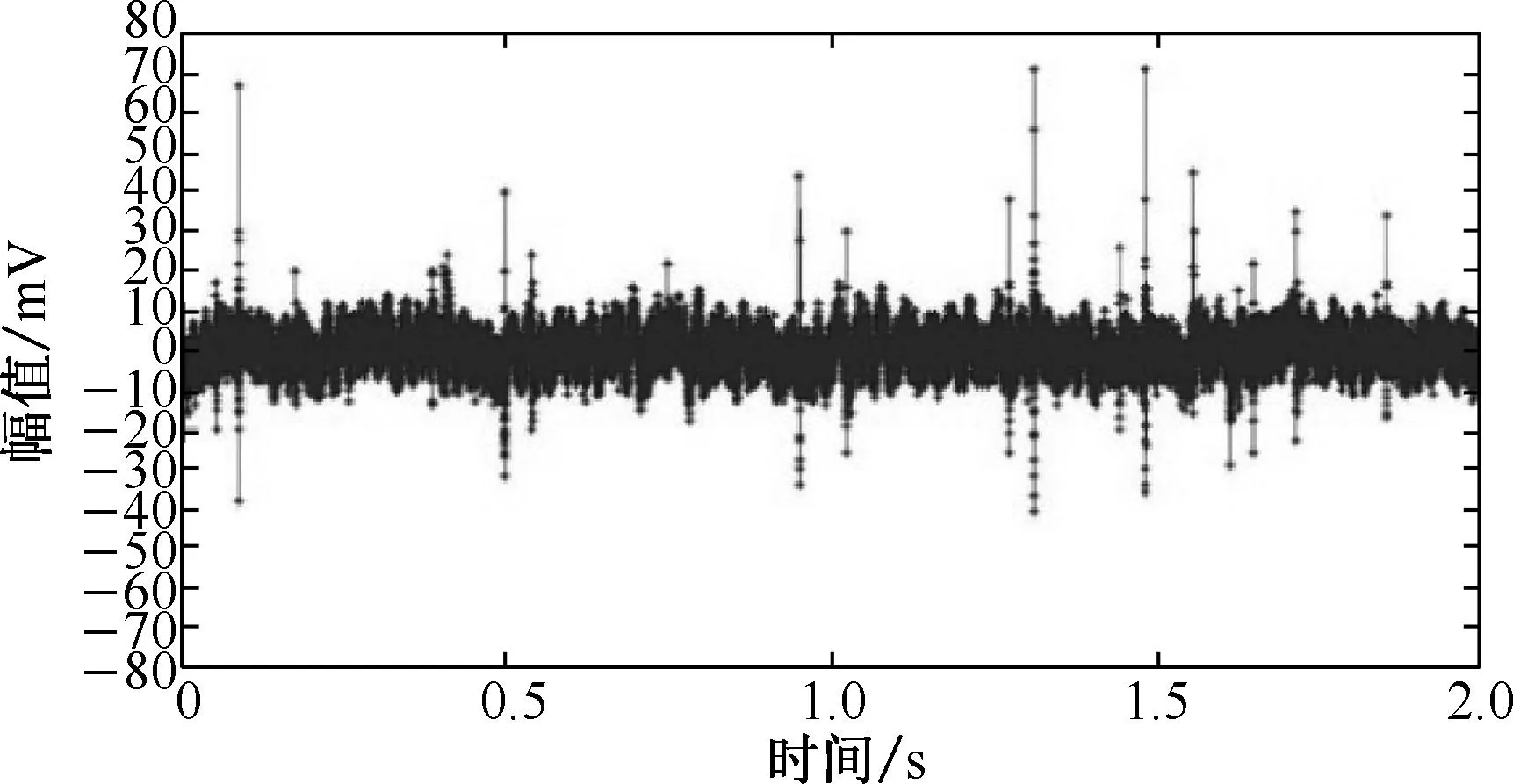
(a) 原始信号

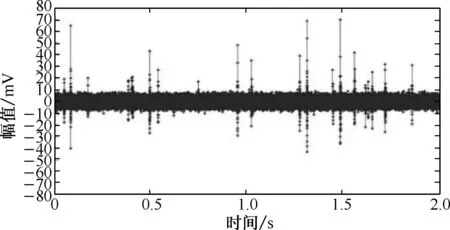
(b) 小波包去除部分背景噪声后信号

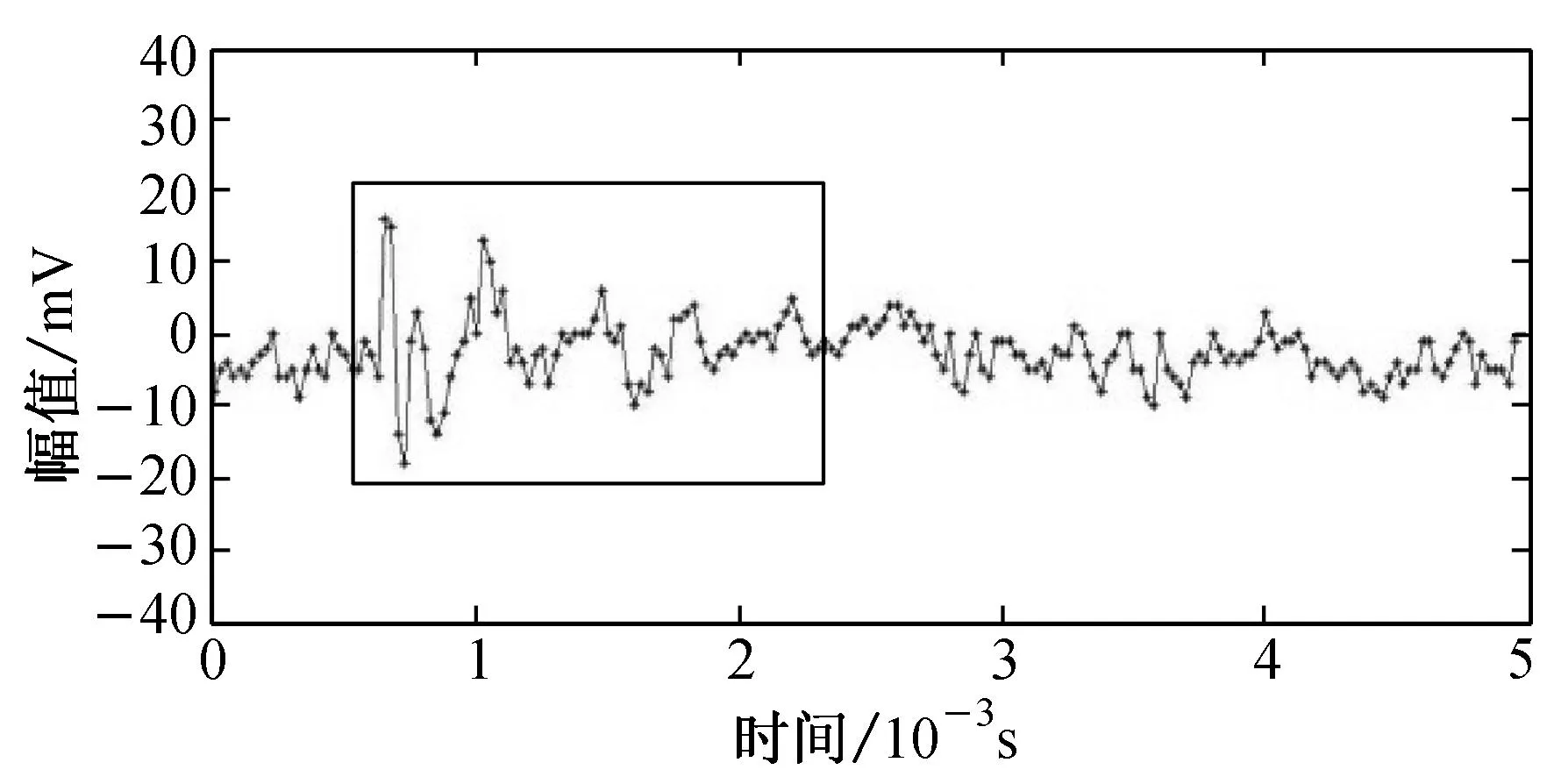
(c) 正负振幅差小于35 mV的信号

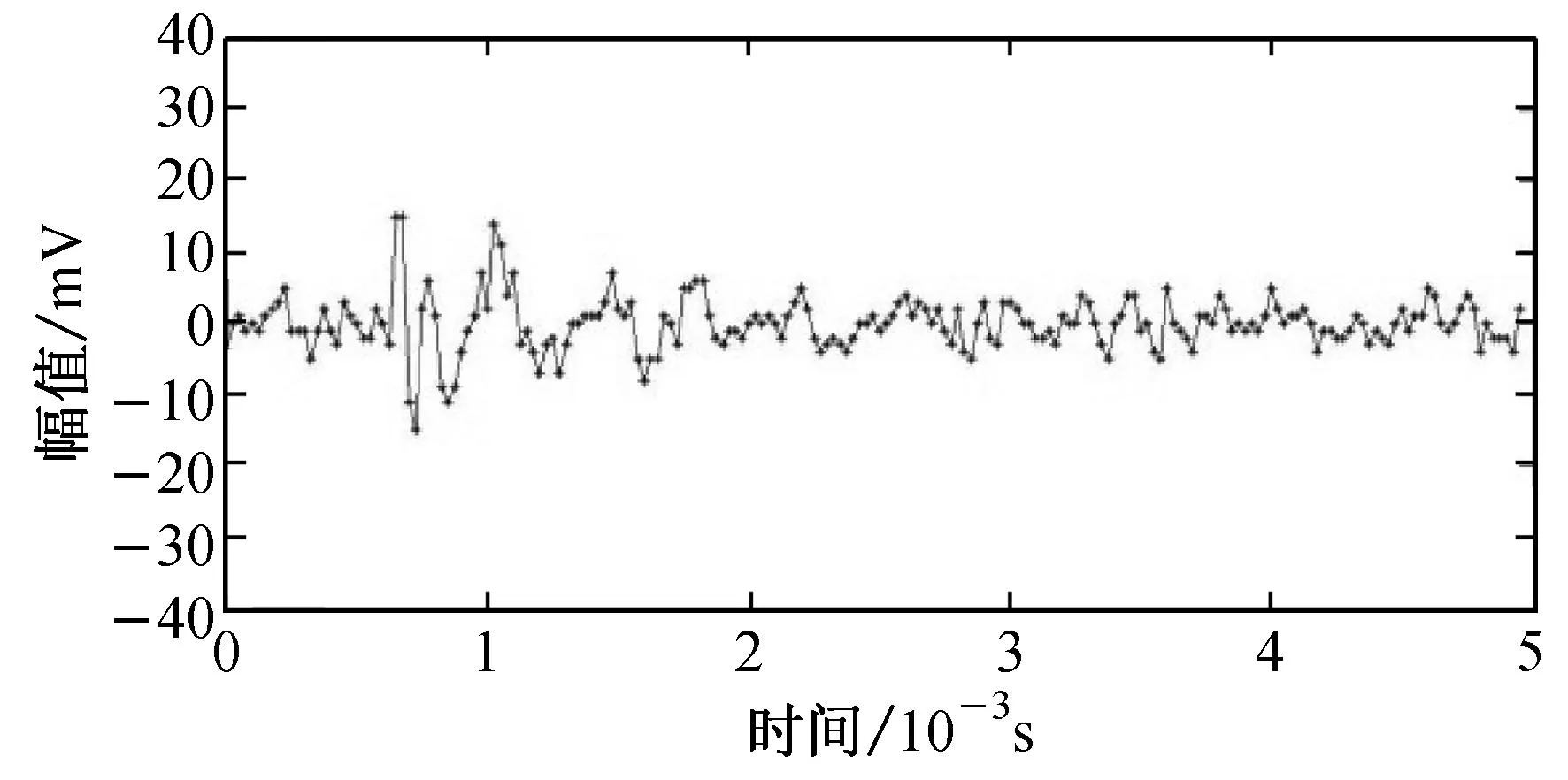
(d) 图(c)经过小波包去噪后信号

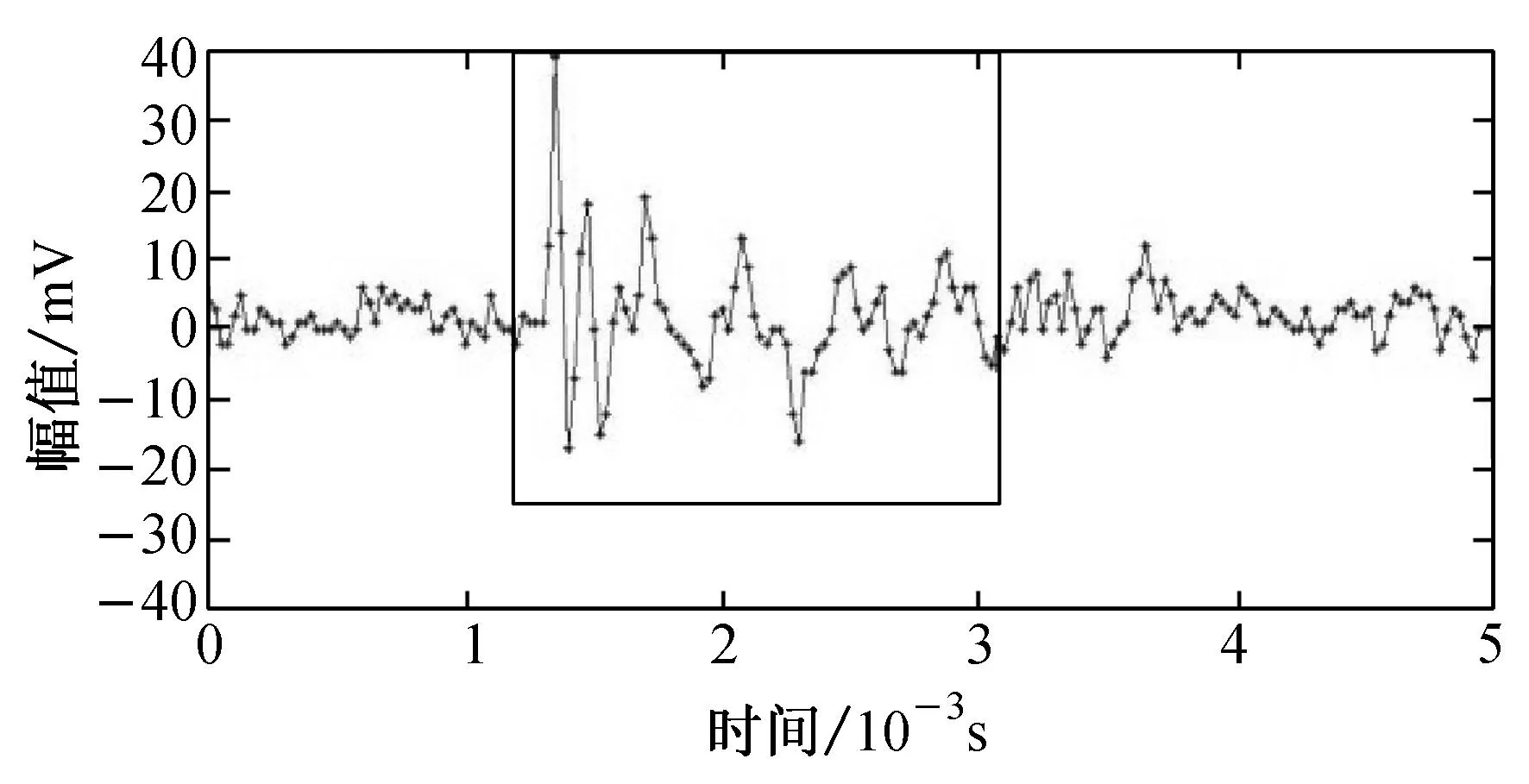
(e) 正负振幅差小于60 mV的信号

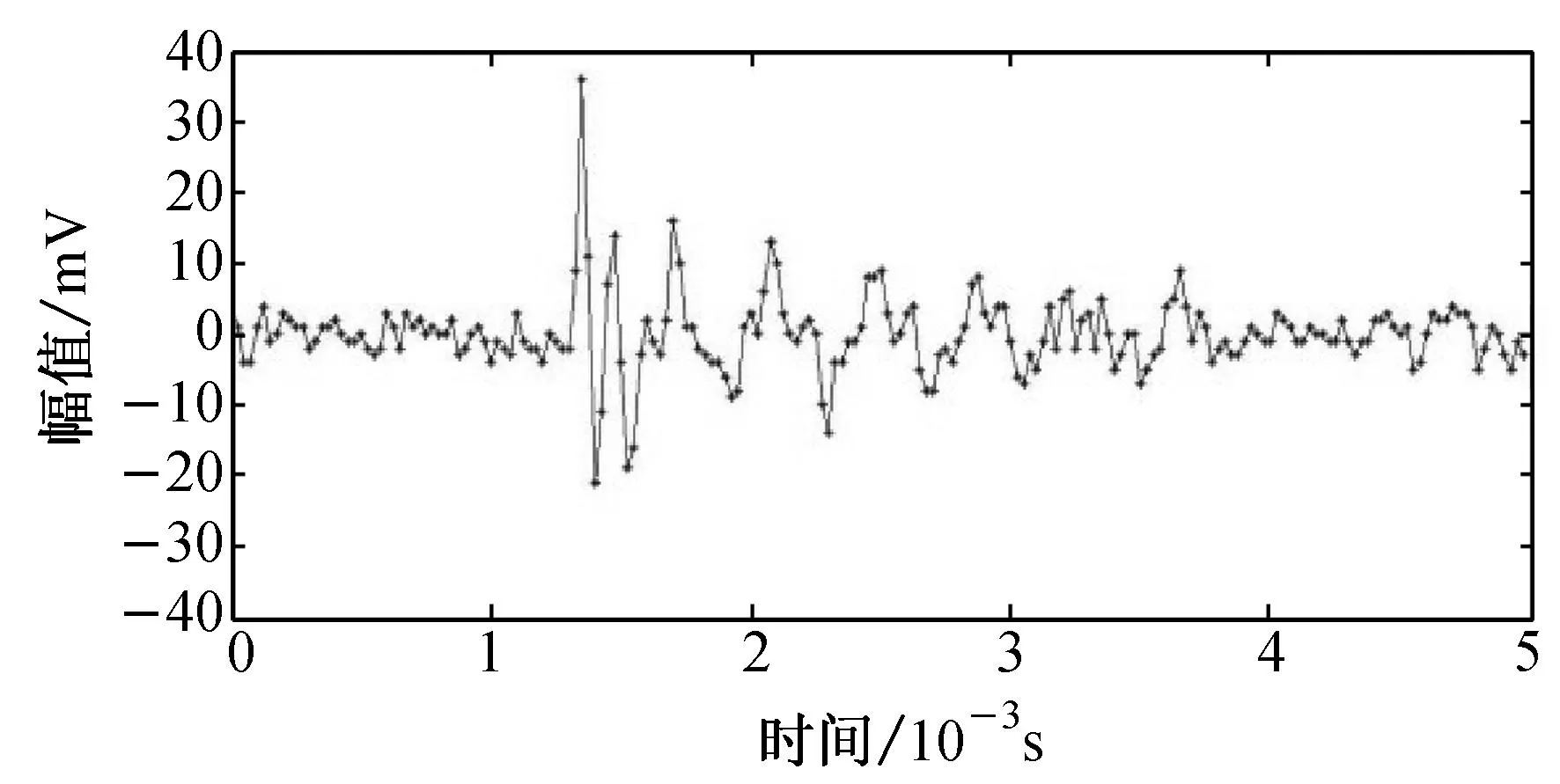
(f) 图(e)经过小波包去噪后信号

其小波包去噪结果如图5(d)所示；正负振幅差在60 mV内的纤维断裂声信号如图5(e)所示，其小波包去噪结果如图5(f)所示. 从图5可以看出，相比于小波去噪，小波包简单去噪不仅能有效地降低背景噪声，而且能较好地保持纤维断裂声信号的原始形态.经过小波包简单去噪后，图5(c)和5(e)两纤维断裂声信号的幅值分别下降了11.8%和7.1%，波形的持续时间和衰减时间基本无变化，声信号的能量减少了18.5%和11.0%.由此可知，小波包去噪的效果明显优于小波去噪的效果，采用小波包去噪可为后续准确提取和识别纤维断裂声信号创造条件.

2.3 纤维断裂声信号波形特征

2.3.1 正负振幅间的幅值差

图6为纤维断裂声信号经小波包简单去噪后的信号，其中，图6(a)为一次拉伸中振幅最小的纤维断裂声信号，图6(b)为一次拉伸中振幅最大的纤维断裂声信号.结合图6和图5(b)可以发现，纤维断裂声信号中存在一正脉冲点(A点，该点的幅值为正振幅)和其后紧跟的一个负脉冲信号点(B点，该点的幅值为负振幅)的幅值差大于背景噪声中任意正脉冲点和负脉冲点的幅值差.因此，可以利用该特征通过设置合适的幅值差阈值，提取纤维断裂声信号和部分瞬态噪声信号，将纤维断裂声信号从背景噪声中提取出来.

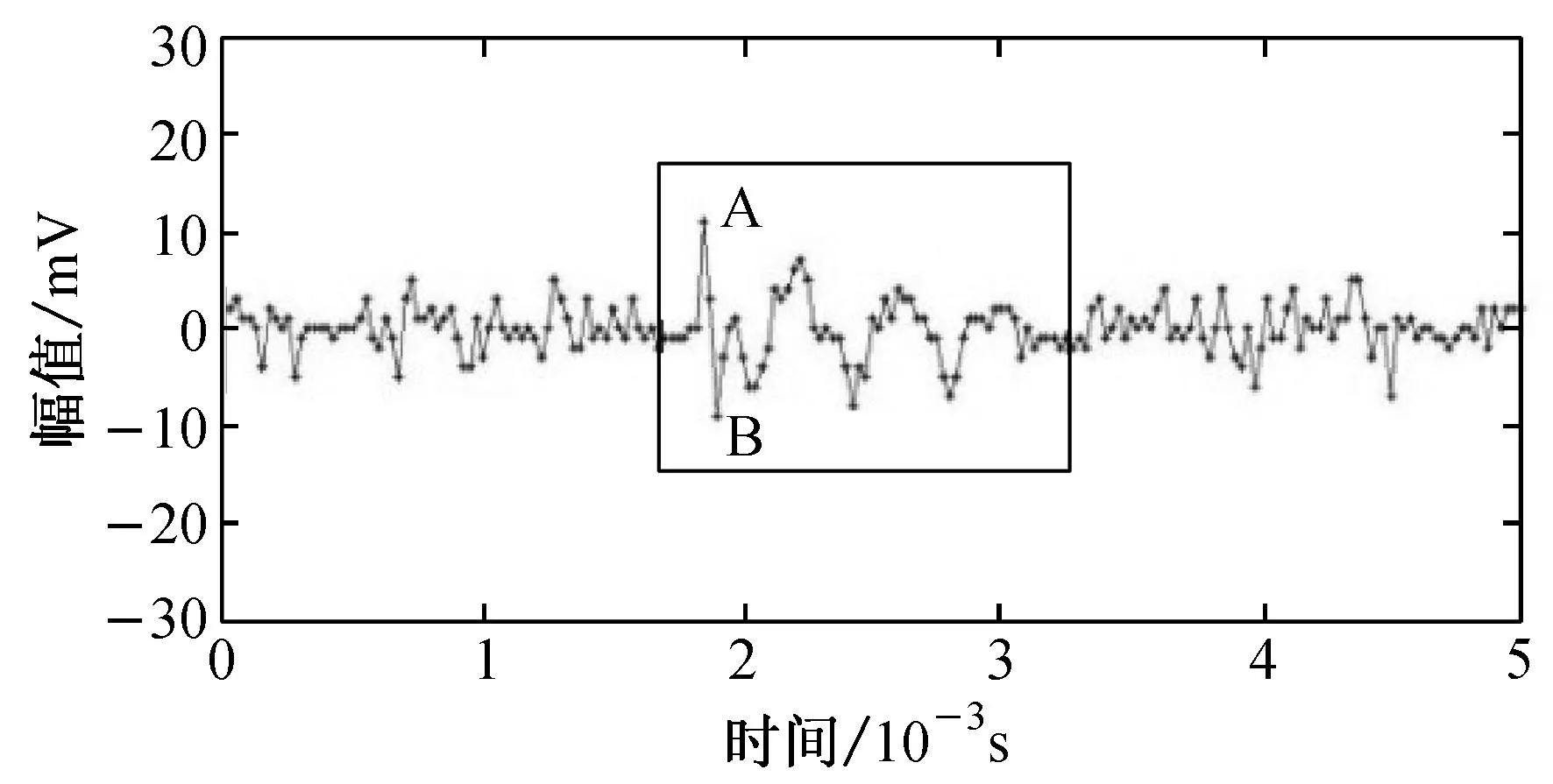
(a) 振幅最小的纤维断裂声信号

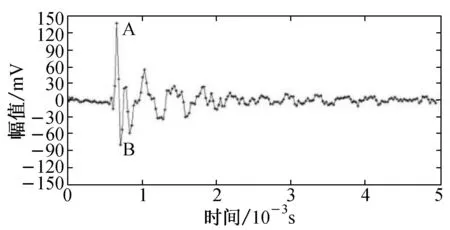
(b) 振幅最大的纤维断裂声信号图6 小波包简单去噪后的信号Fig.6 Results of signal after wavelet-packet denoise

为了取得合适的阈值，取200根无摩擦的纤维，将其分成10组，每组20根，梳理每组纤维，然后将其平行排列于纸上，固定两端，再将200根纤维放到一起进行拉伸.将录取到的声信号进行简单小波包去噪后，对200个纤维断裂声信号正负振幅幅值差进行统计，结果如图7所示. 由图7可以看出，声信号正负振幅幅值差最小为19.94 mV.为了尽可能将疑似纤维断裂声信号从噪声中提取出来而又不提取背景噪声，最终将阈值设定为19.94 mV，该值大于背景噪声的任意两信号点间的幅值差.

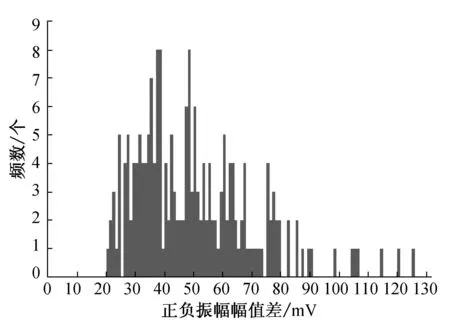
图7 纤维断裂声信号正负振幅幅值差分布图Fig.7 Distribution of the difference between maximum and minimum value of fiber broken signal

在图6(b)的A点前取5个数据点，A点后取74个数据点，这80个数据点(包括A点)可基本构成一个纤维断裂声信号.为了衡量A和B点的对称性，定义对称系数Q，Q为A、 B两点的幅值之和与幅值之差比值的绝对值.经计算可知，图6中两个纤维断裂声信号的Q值均较小，分别为10.0%和26.7%，而图1(c)中瞬态噪声的Q值为60%，远大于26.7%.因而利用纤维断裂声信号的对称性与非对称性，可以去除图1(d)所示类型的瞬态噪声.

2.3.2 纤维断裂声信号频谱特征

数字信号经过傅里叶变换后，可用一系列不同频率的正弦与余弦联合表示，根据正、余弦的频率与其对应系数间的关系，可以得到数字信号的频谱图.纤维断裂声信号产生的机理与瞬态噪声信号不同，因而两者的频率分布也不同.纤维断裂声信号如图8(a)所示, 其频谱图如图8(b)所示；瞬态噪声如图8(c)所示，其频谱图如图8(d)所示.

从图8(b)可以发现，纤维断裂声信号在2 500 Hz处有一个峰值，它位于0～5 000 Hz的低频范围内，这个峰值与纤维断裂声信号存在衰减的余震迹象有关，而余下的如图8(c)类型的瞬态噪声则没有该现象，这是因为瞬态噪声仅有一个孤立的振铃.利用这一频谱特征可以去除余下的瞬态噪声.

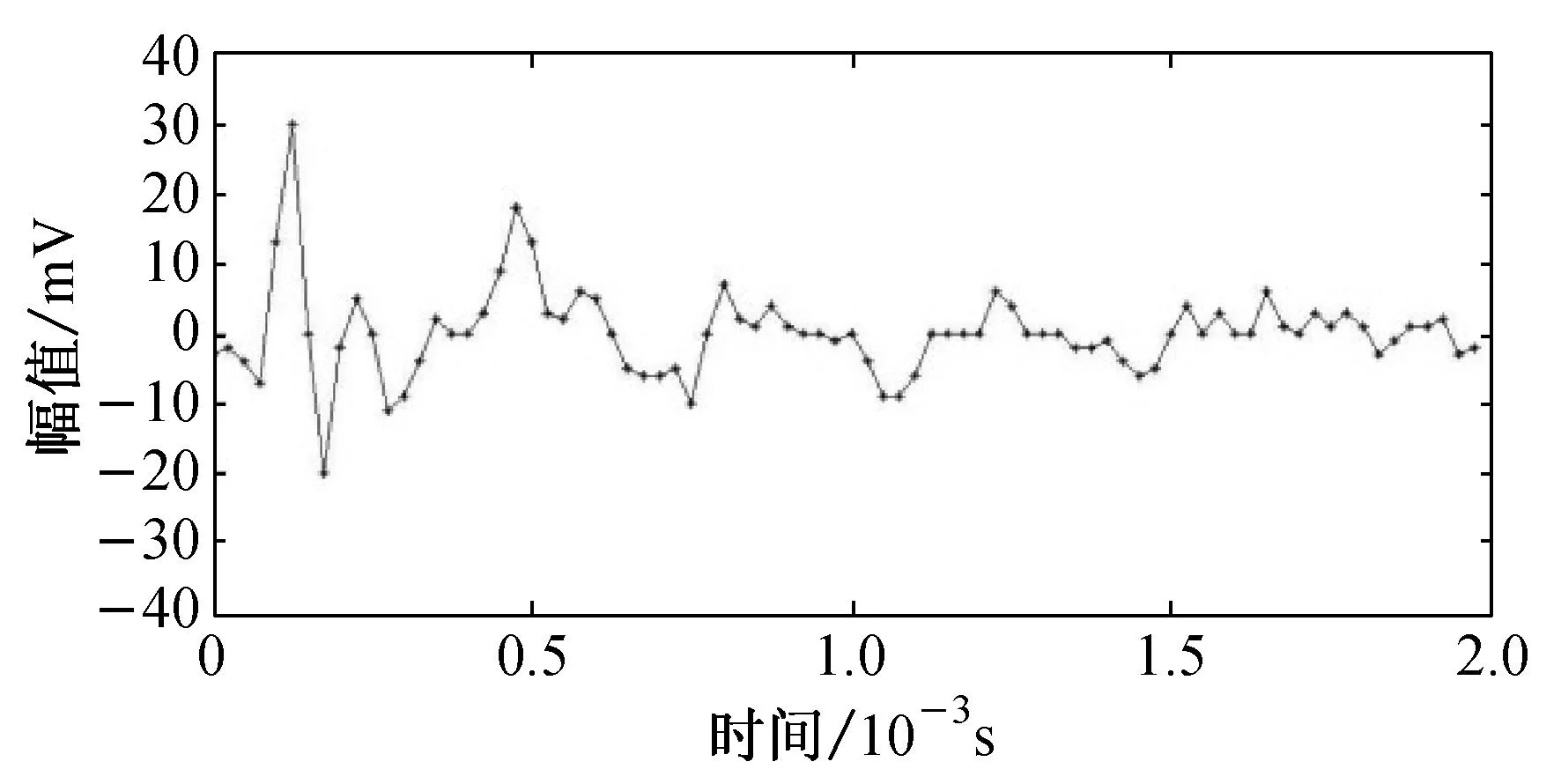
(a) 纤维断裂声信号

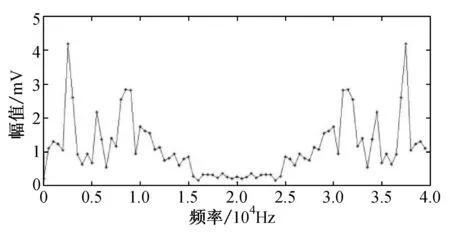
(b) 纤维断裂声信号的频谱图

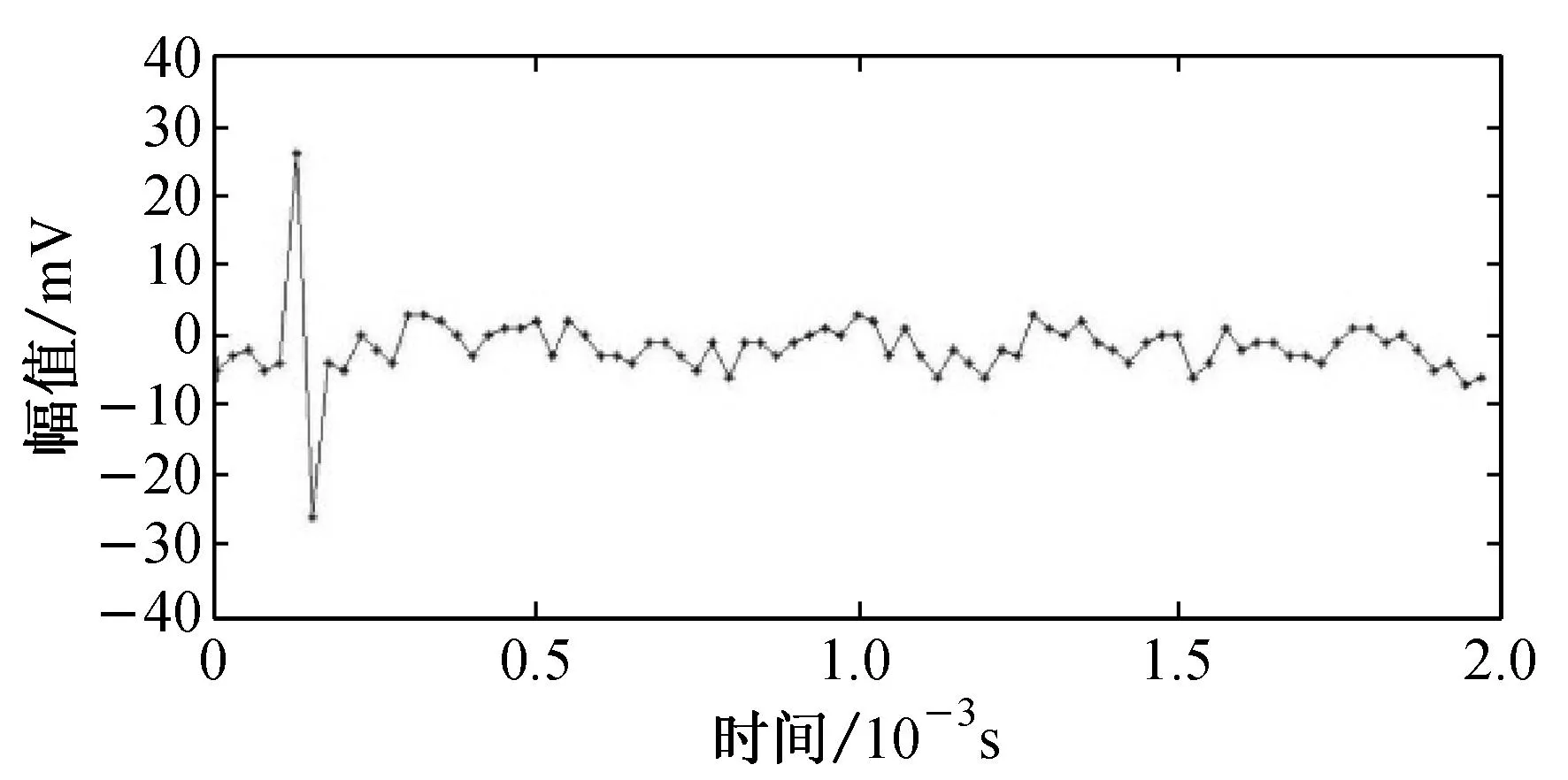
(c) 瞬态噪声

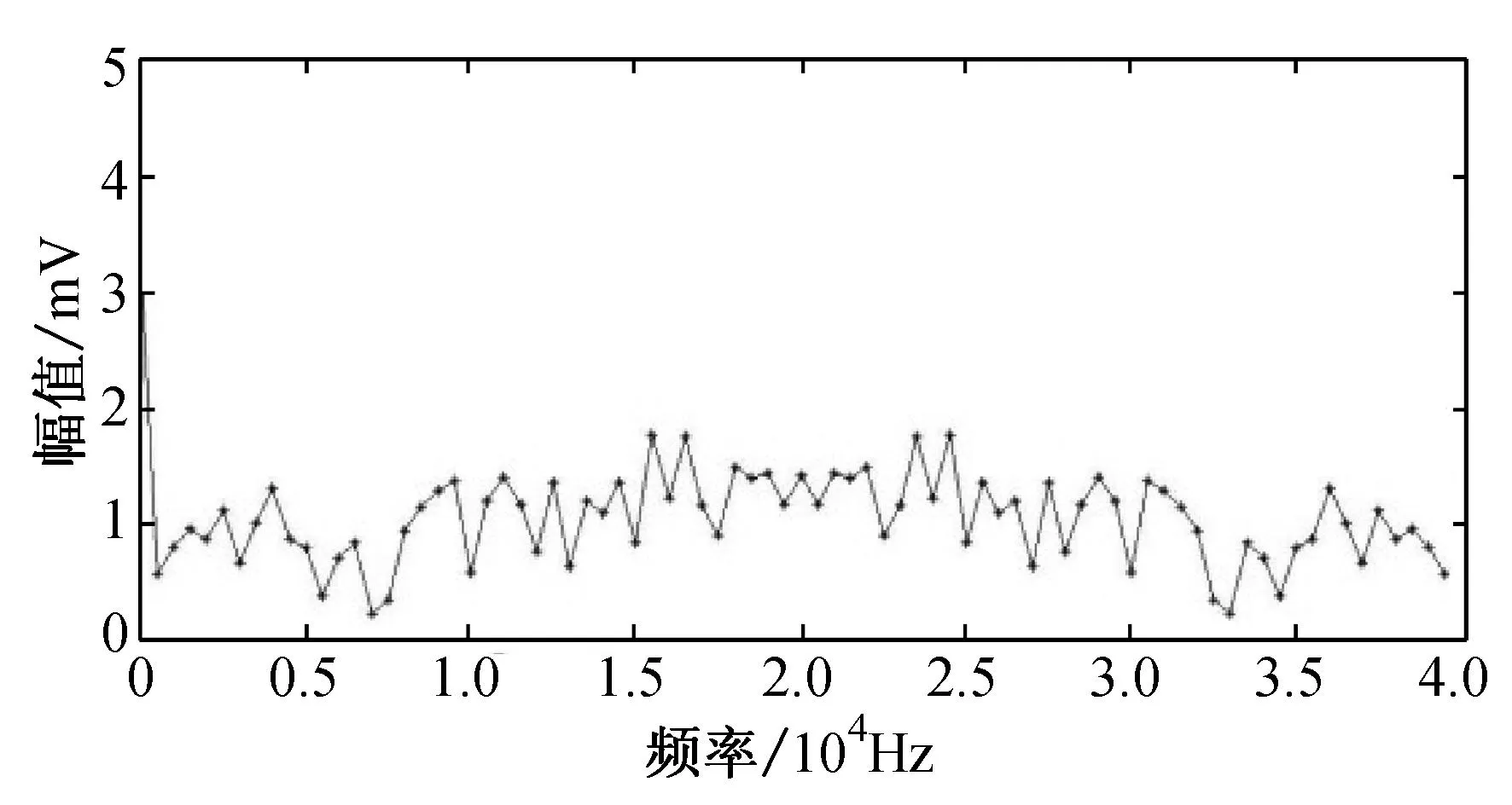
(d) 瞬态噪声的频谱图

3 波形特征和频谱特征组合方法的试验验证

3.1 纤维断裂根数的准确判断

为了验证波形特征和频谱特征组合方法对弱纤维断裂声信号识别的准确性，进行了5次试验.同时采用复合参数法[9]对5次试验的数据进行处理，以验证波形特征和频谱特征组合方法相比于复合参数法在对弱的纤维断裂声信号识别上的优势.试验结果如表1所示.

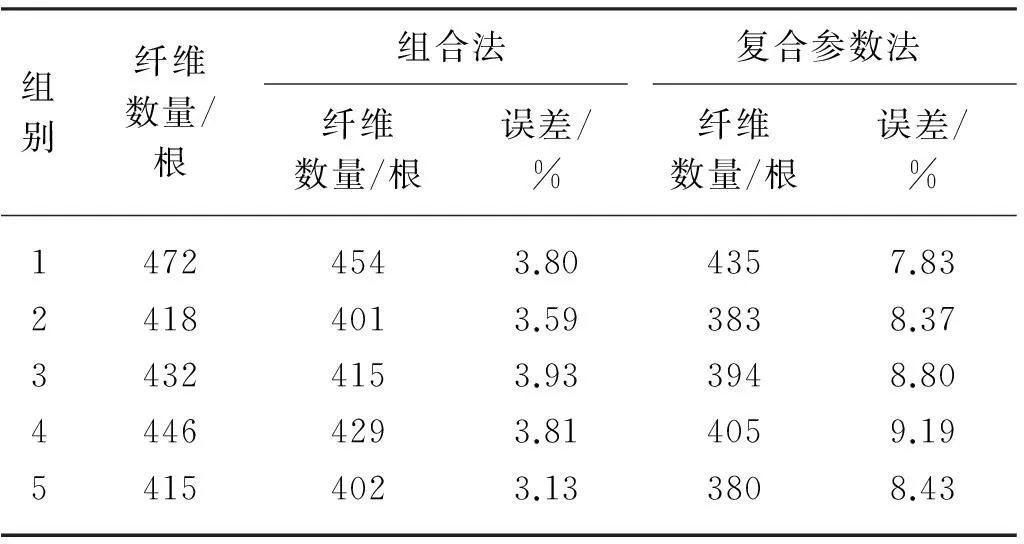
表1 不同方法测量结果的比较

由表1可以发现，组合法的5组试验结果的误差都在4%以内，说明频谱分析方法是稳定且有效的检测方法.从表1还可以发现，每组试验测得的纤维数量均小于检验数量，这可能是因为部分纤维在拉伸过程中发出的声音非常微弱，从而在去噪时被当作噪声去除了，而这种误差约为2%.此外，还存在因两个纤维断裂声信号中部分信号点交叉而导致的误差.复合参数法对弱的纤维断裂声信号识别误差较大(>7.83%)，这是因为小波去噪对信噪比小的纤维断裂声信号的的破坏非常严重.

综合上述分析可以发现，相比于复合参数法，波形特征和频谱特征组合方法在识别弱的纤维断裂声信号上具有优势.

3.2 纤维的断裂伸长率分布

准确识别纤维断裂声信号的主要目的是获得纤维的断裂伸长率分布.在准确识别纤维断裂声信号的基础上，求解纤维的断裂伸长率分布.以表1中纤维数量为472根、检验数量为454根的样本为例，对纤维断裂的时间点进行分析.由图5可以看出，纤维断裂信号的幅度最大点前有5个信号点，声信号的采样频率为40 000 Hz，则纤维断裂信号的幅度最大点与纤维断裂开始的起点之间的时间差约为0.000 1 s，而束纤维拉伸速度为0.11 mm/s，因而可忽略该时间差，将纤维断裂信号的幅度最大点作为纤维拉伸断裂开始点.根据上述分析可以得到纤维断裂伸长率分布直方图如图9所示. 由此表明，在准确识别纤维断裂声信号的基础上，可实现对纤维断裂伸长率分布的求解.

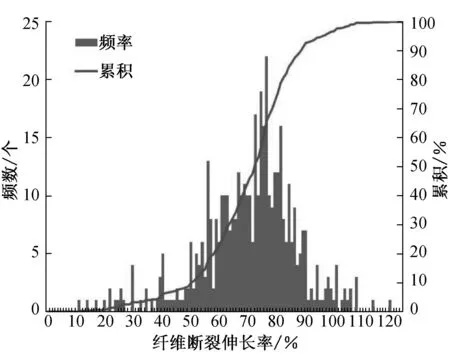
图9 羊毛纤维断裂伸长率分布直方图

4 结 语

本文先利用小波包去噪去除纤维拉伸断裂过程中的部分背景噪声，然后利用纤维断裂声信号中正振幅与负振幅的幅值差大于背景噪声中任意两信号点间的幅值差，将所有背景噪声去除，提取出纤维断裂声信号和部分瞬态噪声信号，再利用纤维断裂声信号的对称性去除部分非对称瞬态噪声.剩余少量的瞬态噪声，则可以通过瞬态噪声与断裂纤维声信号频率分布的差异，对两者进行识别而去除.试验结果表明，波形特征和频谱特征组合方法能有效去除瞬态噪声的干扰，准确判断提取纤维断裂声信号，该方法的误差率小于4%.基于波形特征和频谱特征组合方法可以得到的纤维断裂伸长率分布，相比于复合参数法，该方法对于断裂声信号较弱的羊毛纤维的识别更简便，且误差小.

[1] 于伟东. 纺织材料学 [M]. 北京:中国纺织出版社, 2006:103-104.

[2] DHAVAN K, BHATT H H, RADHAKRISHNAN T. Estimation of tensile properties of single cotton fibers from load-elongation curves of bundles [J]. Textile Research Journal, 1984,54(8):549-551.

[3] SASSER P E, SHOFNER F M, CHU Y T, et al. Interpretations of single fiber, bundle, and yarn tenacity data [J]. Textile Research Journal, 1991,61(11):681-690.

[4] YU W D, DU X F, XIONG H F. Effect of single fibre properties on bundle tensile behavior of wool [J]. Journal of Donghua University, 1992,25(1):9-15.

[5] YU W D, YAN H J, POSTLE R. Evaluating single fiber and fiber bundle tensile curves [J]. Textile Research Journal, 2003，73(10):875-882.

[6] COWKING A, ATTOU A, SIDDIQUI A, et al. Testing E-glass fibre bundles using acoustic emission [J]. Material Science, 1991，26(5):1301-1310.

[7] PAPPAS Y Z, KONTOSOL A, LOUTAS T H, et al. On the characterization of continuous fibres fracture by quantifying acoustic emission and acousto-ultrasonics waveforms [J]. NDT & E International, 2004，37:389-401.

[8] JIHAN S, SIDDIQUI A M, SWEET M A S. Fracture strength of E-glass fibre strands using acoustic emission [J]. NDT and E International, 1997,30(6):383-388.

[9] 毋戈,于伟东,刘洪玲.基于断裂声波形分析的断裂纤维识别与计数[J].东华大学学报(自然科学版),2014,40(1):34-42.

[10] 毋戈.束纤维拉伸中的声与断裂力学的原位表征[D].上海:东华大学纺织学院,2013：62-63.

[11] 管亮,冯新泸.基于小波变换的信号消噪效果影响因素研究及其Matlab实践[J].自动化与仪器仪表,2004(6):43-46.

[12] 胡昌华,张军波,夏军,等.基于MATLAB的系统分析与设计：小波分析[M].3版.西安:西安电子科技大学出版社,2000:7-8.

[13] 陈峰,成新民.基于小波变换的信号去噪技术及实现[J].现代电子技术,2005(3):11-13.

[14] 林克正,李殿璞.基于小波变换的去噪方法[J].哈尔滨工程大学学报,2000,21(4):21-23.

[15] 张毅,杨秀霞.小波消噪在微弱信号检测中的应用[J].微计算机信息,2006,22(1):113-114.

[16] 许天周,黄春光.小波分析理论、算法及其应用[M].北京:国防工业出版社,2007:118-120.

[17] 陈贵亮,王光旭,刘更谦.基于Matlab的小波包μ律绝对值阈值消噪算法的研究[J].科学技术与工程,2013,13(29):8622-8625.

[18] 史贤俊,林飒,李瑞亮.基于最优小波包基的信号去噪算法及其应用[J].海军航空工程学院学报,2006,21(5):506-509.

[19] 蒋玲莉,刘义伦,李学军,等.小波包去噪与改进HHT的微弱信号特征提取[J].振动、测试与诊断,2010,30(5):510-513.

[20] 王首勇,朱光喜,唐远炎.应用最优小波包变换的特征提取方法[J].电子学报,2003,31(7):1035-1038.

Recognition of the Acoustic Signals of Fibers Breaking Based on the Combination of Waveform and Frequency Characters

ZHAOChun-long，YUWei-dong，LIUHong-ling

(College of Textiles, Donghua University, Shanghai 201620, China)

The effects from background noise and transient noises were eliminated, and the precision recognition of the acoustic signals of fibers breaking was realized with a new method which combined waveform and frequency characters. Firstly, some background noise were denoised by wavelet-packet, secondly, residual noise were denoised by using the waveform character and frequency character of the acoustic signals occurred of fibers breaking. The experiments show that the method has low error rate which is less than 4%, and it can be used to evaluate the character of fibers elongation rate availably.

acoustic signals of fibers breaking; wavelet-packet denoising; frequency character; waveform character; distribution of fibers elongation rate

1671-0444(2016)01-0040-07

2014-10-20

赵春龙(1989—)，男，湖北黄冈人，硕士研究生，研究方向为束纤维力学性能的表征.E-mail:2120061@mail.dhu.edu.cn

于伟东(联系人)，男，教授，E-mail: wdyu@dhu.edu.cn

TS 102.1

A