基于蜂群算法多子阵电台天线波束形成*

乔成林，全厚德，崔佩璋，高　飞

（1.军械工程学院，石家庄　050003；2.南京理工大学电子工程与光电技术学院，南京　210094）



基于蜂群算法多子阵电台天线波束形成*

乔成林1，全厚德1，崔佩璋1，高飞2

（1.军械工程学院，石家庄050003；2.南京理工大学电子工程与光电技术学院，南京210094）

摘要：考虑到战场环境下，低信噪比和敌方干扰容易造成超短波电台通信中断，而鉴于天线阵可以有效提高信噪比和抑制干扰，结合战场电台天线分布特点，提出一种多子阵电台天线应急接收模型。理论分析多子阵电台天线波束形成特性，以消除栅瓣、抑制干扰、提高增益为目标，采用蜂群算法对子阵间距进行优化。仿真结果表明，优化子阵间距可以有效消除栅瓣、抑制干扰、提高增益。同时，与遗传算法和粒子群算法相比，蜂群算法具有更好的全局搜索能力和收敛速度。该研究成果可为超短波电台应急通信提供参考。

关键词：电台天线，子阵，波束形成，栅瓣，蜂群算法

0　引言

军用超短波电台具有通信距离远、保密性好等优点，在战场通信中起着重要作用。然而，战场环境由于其本身特殊性，电台通信会面临种种突发情形，导致电台无法正常通信，甚至中断。因此，研究一种应急通信模型保证电台通信正常显得尤为重要。

子阵波束形成技术最初出现在大型阵列波束形成中，由于大型阵列中基于阵元级波束形成是非常复杂和极其昂贵的。有学者提出将大型阵列划分为若干个子阵，研究基于子阵级波束形成技术，取得了较好效果［1-2］。战场中电台虽然是一个独立通信个体，但从其射频段取出信号是可行的，并通过同轴电缆将该信号导出处理，从而实现电台天线组阵。此时将每个通信车看成一个子阵，通信车上每个电台天线看成一个阵元。文献［3-5］指出子阵间距超过一个波长时，方向图中会产生栅瓣，而优化子阵间距可以消除栅瓣、提高增益。但文献［3-4］并未考虑子阵间距约束，文献［5］采用的天线阵元是有向的，而本文背景需要考虑子阵间距约束，并且采用的天线阵元是全向的。

子阵级波束形成问题实际上是子阵位置的非线性函数优化问题，目前尚无解析方法求解。近年来，差分进化算法［6］、遗传算法［7］和粒子群优化算法［8］等寻优算法被广泛应用于阵列波束形成求解中，这些算法各有利弊，但均容易陷入局部极值。2006年D.T. Pham等人提出运用蜂群算法解决复杂寻优问题［9-10］，该算法算法能够快速收敛到全局最优值同时避免陷入局部最优值。

为此，本文针对战场环境下，低信噪比和易受敌方干扰容易造成电台通信中断的缺陷，提出多子阵电台天线应急接收模型，并采用蜂群算法优化子阵间距，达到消除栅瓣、抑制干扰、提高增益的目的。

1　多子阵电台天线应急接收模型

将通信车看成一个子阵，通信车上每个电台天线看成一个阵元。假设所有电台天线在同一平面，建立如图1所示的多子阵电台天线应急接收模型。L为子阵的个数（通信车数目），D为天线阵的孔径（所有通信车间距总和），di（i=1，2，…，L-1）为子阵间距（相邻通信车间距），M×N为每个子阵内的天线单元数（通信车上电台天线个数），dx、dy分别为子阵内相邻阵元在X轴和Y轴上的间距，准为入射信号方位角，θ为入射信号俯仰角。

图1多子阵电台天线应急接收模型

根据方向图相乘原理，子阵方向图函数表示为：

其中，am（m=1，2，…，M），bn（n=1，2，…，N）分别是子阵内X轴、Y轴上阵元幅度加权值；k=2π/λ为来波信号的空间波数；βx、βy是子阵内阵元相位延时。

阵因子方向图函数表示为：

其中，wl（l=1，2，…，L）是子阵幅度加权值，δl（l=2，3，…，L）是子阵相位延时。

由于各个子阵结构是相同的，则它们的方向图函数也是相同的，根据方向图相乘原理，由式（1）、式（2）可知多子阵电台天线方向图函数为：

为了不失一般性，假设入射信号俯仰角θ=90°，则多子阵电台天线方向图函数为：

2　多子阵电台天线方向图分析

为研究多子阵电台天线方向图特性，现对均匀间距时方向图进行分析。

本文以美军SINCGARS系列超短波电台为例，其工作频段为30 MHz~87.895 MHz［11］。假设此时工作方式为定频（跳频工作模式不在本文研究范围）。

仿真参数设置为：期望信号方向准0=（0°，90°），M=2，N=2，L=8，dx=3 m，dy=4 m，D=120 m，子阵间距d=17.1 m，f=50 MHz（λ=6 m），am=1（m=1，2，…，M），bn=1（n=1，2，…，N），wl=1（l=1，2，…，L），仿真时采用理想条件，忽略阵元互耦等因素的影响。仿真结果如下页图2和图3所示，图2为不加幅度激励子阵方向图和阵因子方向图，图3为不加幅度激励和加-20 dB切比雪夫幅度激励合成方向图对比。

图2不加幅度激励子阵方向图和阵因子方向图

图3两种情形下合成方向图比较

结合理论分析和仿真结果可得到以下两点结论：

从上述结论中可知消除栅瓣有以下两种方法：

①改变子阵方向图，减小子阵主瓣宽度。降低主瓣宽度可通过增加子阵内阵元数或采用有方向性的阵元等方法。而在本文中通信车上的电台天线数目和位置都是固定的，且电台天线是全向的。

②改变阵因子栅瓣位置，使栅瓣不在子阵主瓣内。分析可知栅瓣产生的位置与波长和子阵间距有关，结合本文实际，通信车的位置是可以移动的即子阵间距是可以改变的，通过改变子阵间距使得栅瓣不在主瓣内从而达到消除栅瓣的目的。

3　多子阵电台天线的蜂群算法优化

3.1蜂群算法（BA）基本原理

根据自然界蜂群觅食过程，2006年D.T. Pham等人提出蜂群算法用于解决复杂寻优问题，并验证了该算法与其他寻优算法相比，具有更好地全局搜索能力且不易陷入局部极值［9-10］。根据蜂群采蜜过程，构造蜂群算法，该算法包含下列参数：侦查蜂数量（n）、从侦查蜂中选择精英蜂和非精英蜂的数目（m）、精英蜂数量（e）、跟随蜂跟随精英蜂的数目（n1）、跟随蜂跟随非精英蜂的数目（n2）、跟随蜂邻近搜索片区的大小（n3）、控制邻近搜索片区大小的参数（cf）和停止准则。具体算法流程图如图4所示：

图4蜂群算法流程图

蜂群算法的邻近空间搜索描述如下：

假设B（s，i）=（d1，d1，…，dL-1）指第i代第s个寻优蜜蜂，则该蜜蜂的邻近搜索空间表示为：

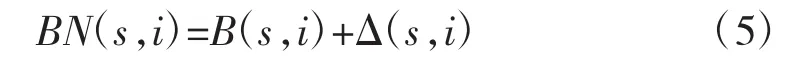
其中，n3表示被选择片区大小，rl（l=1，2，…，L-1）在区间［-0.5，0.5］内随机变化，cf控制邻近搜索空间的大小，随之迭代次数上升cf减小，最后算法收敛于某一个最优解。

3.2蜂群算法（BA）适应度函数

根据上文所述采用蜂群算法优化子阵间距，可以有效消除栅瓣、抑制干扰、提高增益。根据实际使用情况，通信车之间应满足最小间距约束和孔径约束，即子阵间距不应小于dmin、孔径大小不变。所以优化函数设置为：

其中，SLLmax是最大峰值旁瓣电平，F（准NULL，θNULL）是零陷电平，c1，c2是加权系数。

仿真中子阵间距在变化过程中很可能不再满足最小间距要求，为了保证子阵间距满足最小间距要求，采取文献［6］设定一个间距约束矩阵。由子阵数L和最小子阵间距dmin确定间距约束矩阵为：

H=［0 d 2d…（L-1）d］（7）

同时为了保证阵列孔径，优化时起始端和末端子阵不动。假设前L-1个阵元均向后占据长度d，则有（L-1）d长度不能分布阵元，剩余长度为：

U=D-（L-1）d（8）

在［0，U］内随机生成L-2个数，并按从小到大排列，记为向量P=［0 p1p2…U］。在蜂群算法优化过程中，计算适应值函数前执行操作：

S=P+U（9）

通过上述步骤保证了子阵满足最小间距约束和阵列孔径约束。

4　仿真实例

本文以美军系列超短波电台为例，其工作频段为30 MHz~97.895 MHz［11］。假设此时的工作方式为定频（跳频工作模式不在本文研究范围）。另外，考虑到实际，子阵（通信车）位置优化到分米级。

仿真实例1：无干扰条件下优化子阵间距期望信号方向准0=（0°，90°），M=2，N=2，L=8，dx=3 m，dy=4 m，D=120 m，最小间距dmin=10 m，f=50 MHz（λ=6 m），am=1（m=1，2，…，M），bn=1（n=1，2，…，N），wl=1（q=1，2，…，L）。蜂群算法参数为：n=200，e=1，m=10，n1=110，n2=10，n3=1，cf=3，c1=1，c2=0，最大迭代次数为300。表1列出了仿真优化后子阵间距，图5为子阵间距优化前后合成方向图对比。由图5可知，子阵间距优化后最大峰值旁瓣电平为-11.12 dB，比优化前下降了8.508 dB。结合表1可知，子阵位置优化到分米级更加接近实际。因此，采用蜂群算法优化子阵间距可以有效降低消除栅瓣、提高增益。

仿真实例2：蜂群算法寻优性能

期望信号方向准0=（0°，90°），M=2，N=2，L=8，dx=3m，dy=4 m，D=120 m，最小间距dmin=10 m，f=50 MHz（λ= 6 m），am=1（m=1，2，…，M），bn=1（n=1，2，…，N），wl=1 （q=1，2，…，L）。蜂群算法参数为：n=200，e=1，m=10，n1=110，n2=10，n3=1，cf=3。遗传算法参数为：n=200，交叉概率Pc=0.9，变异Pm=0.2。粒子群算法参数为：n=200，惯性权重w=0.5，加速常数c1=2，加速常数c2=2。最大迭代次数均为300。图6为经过20次随机仿真后3种算法平均收敛曲线。从图6可知，与GA和PSO相比，BA具有更好的全局搜索能力和收敛速度。

表1仿真优化后子阵间距

图5无干扰下间距优化后合成方向图

图6 BA、GA和PSO收敛曲线

仿真实例3：干扰条件下优化子阵间距

期望信号方向准0=（0°，90°），干扰信号方向准int= （-30°，90°），M=2，N=2，L=8，dx=3m，dy=4 m，D=120 m，最小间距dmin=10 m，f=50 MHz（λ=6 m），am=1（m=1，2，…，M），bn=1（n=1，2，…，N），wl=1（q=1，2，…，L）。蜂群算法参数为：n=200，e=1，m=10，n1=110，n2=10，n3=1，cf=3，c1=12，c2=1，最大迭代次数为300。表2列出了仿真优化后的子阵间距，图7为子阵间距优化前后合成方向图对比。由图7可知，子阵间距优化后最大峰值旁瓣为-10.05 dB，比优化前下降了7.438 dB，干扰方向零陷深度为-72.91 dB。结合表2可知，子阵位置优化到分米级更加接近实际。因此，采用蜂群算法优化子阵间距可以有效降低消除栅瓣、抑制干扰、提高增益。

表2仿真优化后子阵间距

图7干扰下间距优化后合成方向图

5　结论

本文结合战场应用实际，将每个通信车看成一个子阵，通信车上每个电台天线看成一个阵元，提出多子阵电台天线应急接收模型。通过理论分析和仿真实例表明，优化子阵间距可以有效消除栅瓣、抑制干扰、提高增益，从而保证战场正常通信。同时，与遗传算法和粒子群算法相比，蜂群算法具有全局搜索能力和收敛速度。本文研究结果可为战场超短波电台应急通信提供参考。考虑到保密需要，战场中超短波电台将采用跳频通信模式，针对此种情形，下一步将继续研究。

参考文献：

［1］葛佩.基于子阵划分的自适应波束形成技术［D］.西安：西安电子科技大学，2012.

［2］张旭红，李会勇，何子述.平面数字阵列雷达的子阵级波束形成算法［J］.雷达科学与技术，2008，6（6）：440-444.

［3］HIRATA K，NISHIZAWA K，MATAUDA S，et al. Experimental evaluation of capon’s beam former applied to anon-uniformly arranged distributed array［C］// International Symposiumon Antennasand Propagation，2006.

［4］HIRATA K，NISHIZAWA K，MATAUDA S，et al. Experimental investigations into grating lobe suppression in distributed array antennas［C］// International Symposium on Antennas and Propagation，2006.

［5］LIN Z Q，YAO M L，SHEN X W. Sidelobe reduction of the low profile multi-subarray antenna by genetic algorithm［J］. International Journal of Electronics and Communications，2012，66（2）：133-139.

［6］宋晓侠，郭陈江，丁君.基于改进的差分进化算法的非均匀阵列综合［J］.探测与控制学报，2012，34（4）：71-74.

［7］GOSWAMI B，MANDAL D. A genetic algorithm for the level control of nulls and side lobes in linear antenna arrays［J］. Journal of King Saud University-Computer and Information Sciences，2013，25（2）：117-126.

［8］KADRI B，BRAHIMI M，ELAWADY I，et al. Fuzzy genetic versus PSO algorithms for the synthesis of linear antenna array［C］// International Conference on Advances Science and Contemporary Engineering，2012.

［9］PHAM D T，GHANBARZADEH A，KO E，et al. The bees algorithm-a novel tool for complex optimisation problems［J］. Intelligent Production Machines and Systems，2006（3）：454-459.

［10］GUNEY K，ONAY M. Bees algorithm for interference suppression of linear antenna arrays by controlling the phase-only and both the amplitude and phase［J］.Expert Systems with Applications，2010，37（4）：3129-3135.

［11］梅文华，王淑波，邱永红，等.跳频通信［M］.北京：国防工业出版社，2005.

Research of Radio Antenna with Multi- subarrays Beam Forming Based on Bees Algorithm

QIAO Cheng-lin1，QUAN Hou-de1，CUI Pei-zhang1，GAO Fei2
（1.Ordnance Engineering College，Shijiazhuang 050003，China；2. Electtronic Engineering and Optoelectronic Technology，University of Science and Technolgy，Nanjing 210094，China）

Abstract：VHF radio communication is easily interrupted by low Signal to Noise Ratio（SNR）and directional interference in the battlefield environment. The antenna array can improve the SNR and suppress the interference effectively. Combined with the characteristic of VHF radio in the battlefield，a radio antenna with multi -subarrays emergency receiving model is proposed. The characteristics of pattern synthesis of radio antenna with multi-subarrays are analyzed theoretically. In order to remove the grating lobe，suppress the interference and improve the gain，the Bees Algorithm（BA）is applied to optimizing the subarray distances. The simulation result indicated that optimizing the subarray distances can remove the grating lobe，suppress the interference and improve the gain effectively. When compared with Genetic Algorithm（GA）and Particle Swarm Optimization（PSO）algorithm，BA has a better global search ability and convergence speed. The research can provide a reference for emergency communication of VHF radio.

Key words：radio antenna，subarray，beam forming，grating lobe，bees algorithm

作者简介：乔成林（1990-），男，安徽天长人，硕士研究生。研究方向：阵列天线信号处理。

*基金项目：军队科研基金资助项目

收稿日期：2015-01-07

文章编号：1002-0640（2016）02-0153-05

中图分类号：TN820

文献标识码：A

修回日期：2015-03-12