战场运动目标快速跟踪研究*

李　思，关兴来，宁俊帅

（1.军械工程学院，石家庄　050003；2.中国洛阳电子装备试验中心，河南　孟州　454750）



战场运动目标快速跟踪研究*

李思1，关兴来2，宁俊帅1

（1.军械工程学院，石家庄050003；2.中国洛阳电子装备试验中心，河南孟州454750）

摘要：针对现有的基于图像序列目标提取算法HS算法和LK算法过于复杂、运算量大等缺点，提出了快速微分光流法，并利用Matlab仿真实验验证了该技术的可行性。

关键词：HS算法，LK算法，光流法

0　引言

战场侦察设备的运动目标提取和测量［1］与民用系统相比，有着不同的特点。根据对战场侦察图像信息［2］的分析，其需要处理的图像中的运动目标具有以下特点：

（1）目标在图像中的投影面积小

战场环境中，由于被侦察的目标一般都处于距离较远的位置，无论单个还是多个目标，其投影面积均远小于图像背景面积。一般情况下，侦察图像目标投影所占的像素面积小于图像总面积的1/5。

（2）目标零散

现代战争条件下，兵力部署和运用密度远低于传统作战，战场上各作战单位之间距离较远。反映在图像上，目标之间的距离远大于目标本身的尺寸。

（3）目标外形复杂

战场上目标形状非常复杂，无论单兵还是装备，其外形和运动都很非常不规则，目标的不同部分其特征差别也较大。

现有的基于图像序列的运动目标测量和提取的各种光流算法已经在民用领域广泛应用，但还不能满足军事侦察应用的需求。其主要原因是：

（1）算法过于复杂，计算量大，不适合实时条件下使用；

（2）现有算法大都针对某一民用领域的特殊条件，不能适应在复杂的战场环境。

针对现有光流法Lucas-Kanade算法［3］和Horn Schunck算法［4］的缺点，本文提出了快速微分光流法，并利用Matlab软件验证了该技术的可行性。

1　基于图像序列快速微分光流法

光流法是根据目标运动产生的图像中相关像素的灰度和亮度变化来对目标的运动状态进行测量。当某个像素点的邻域内各点的灰度梯度方向一致时，Horn Schunck算法是将物体运动速度在像素梯度方向上的分量取代物体真实的运动速度值。此时求得的光流值大小如式（1）所示：

m=m0cosθ（1）

式（1）中m0表示物体真实的运动速度值的大小，θ表示物体运动方向和像素灰度梯度方向的夹角，见图1所示。

图1光流值的大小和方向

如图1所示，速度的分解是在［-90°，90°］范围内进行。当真实速度方向和梯度方向的夹角大于90°时，速度的分解方向其实是梯度方向的反向延长线方向。因此，求得的速度分量的方向变化范围是［θ0-90°，θ0+90°］，其中θ0是真实速度方向角。

当物体在像面上的投影面积较大时，如果此时选择邻域窗口很小，那么可能有较多像素点是采用运动速度像素梯度方向上的分量取代物体真实的运动速度值。如图2所示为连续视频中前后两帧连续的图像。

图2连续视频中的两帧图

将物体运动速度在像素梯度方向上的分量作为物体真实的运动速度值，求出光流场，如图3所示。

从图3可以看出，运动物体各处光流值大小和方向不同。可以采用对运动物体上各点在较大邻域内求均值的方法，求出方向和大小较一致的光流值。下面分析此时光流值的误差大小。

在邻域内求均值后，各像素的光流值为：

式（2）中，p为点（x，y）的邻域，（xi，yj）为邻域p中的像素，m軖（xi，yj）为像素的光流矢量。

图3光流方向杂乱

对于光流场中任何和物体运动方向不一致的光流值，均可以分解为与运动方向相同的光流值和与运动方向垂直的光流矢量，即：

如果求均值的邻域范围足够大，那么在邻域内的像素点较多。因为各个像素点的梯度方向呈均匀分布，即邻域内梯度在各个方向的像素点数量应该均匀相等，所以与物体运动方向垂直的光流矢量中，角度为θ0+90°和θ0-90°的光流矢量数量应该相等，且光流矢量的大小分布应该相同。因此，这两个角度的光流矢量可以互相抵消，即：

那么可以得出均值的大小为

上式表明，邻域内不同方向的光流值的均值大小等于各像素点光流在物体运动速度方向分量的均值。其值的大小为：

由于θ值为均匀分布，因此：

根据上述结论，得出下面的求光流场的公式：

上式即是快速微分光流法的公式。求取光流场的目的，是将光流作为提取目标的指标，对图像中每一点的光流值乘以2再除以n，并不影响目标和背景之间的差别，因此，在不要求确切数值时，为了简化计算可以将式（9）改为：

为消除测量误差，本文引入参数矩阵：

式（11）中，Un为横向光流u的参数矩阵，Vn为纵向光流v的参数矩阵，Fx，Fy分别表示横向和纵向的灰度梯度矩阵，δ是阈值，sign（）是符号函数，即若括号内的参数为正，则值为1；若参数为负，则值为-1；若参数为0，则值为0。因此，可以将求均值的公式改为式（12）：

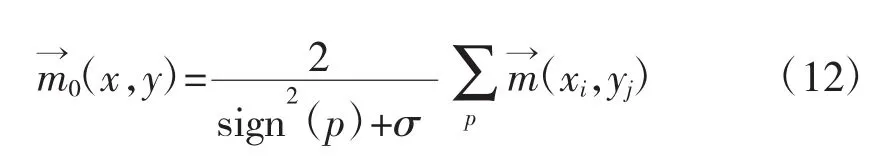
2　快速微分光流法时间复杂度

表1给出了这两种算法在其求均值的邻域内包含的像素数不同时各种运算次数的对比，表中Lucas-Kanade算法采用初等变换法法求逆矩阵。从表中可以看出。Lucas-Kanade算法所需乘除法的时间复杂度是O（n）。

表1快速微分算法和LK算法时间复杂度对比

3　光流算法对比实验

首先从分别从3个视频中各选出1组连续图像——如图4~图6中的（a）和（b）所示，分别采用Lucas-Kanade算法和快速微分光流法进行处理，求出其光流场。在实验中，两种算法的每个像素的邻域窗口均按3×3设置。

图4视频1处理结果

图5视频2处理结果

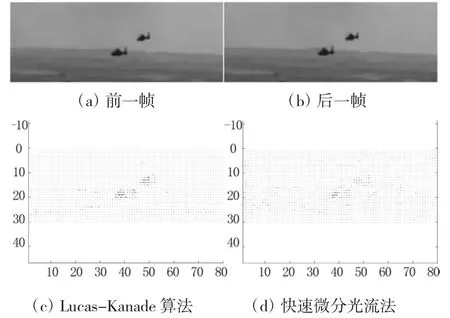
图6视频3处理结果

通过观察光流场图形，可以判断，两种算法测得的光流场大致相当。第12页表2是快速微分光流法和Lucas-Kanade算法处理时间和精度的具体数值对比。

由表2可以得出：快速微分光流法的计算时间仅仅是Lucas-Kanade算法的约1/10，快速微分光流法的处理速度要明显快于Lucas-Kanade算法。另外，与Lucas-Kanade算法相比，快速微分光流法存

表2快速微分光流法和Lucas-Kanade算法处理时间即精度对比

在的相对误差大约在10%~20%。在实际的侦察图像中，目标图像所占有的面积不到总面积的1/5，目标区域的光流值大约是背景区域的4倍，因此，10% ~20%的误差不影响图像分割的结果，快速微分光流法能够满足分割和标记目标的要求。

4　结论

本文针对现有光流算法过于复杂、运算量大等缺点，提出了快速微分光流法，最后通过Matlab仿真实验对LK算法和快速微分光流法进行了比较，验证了该技术的可行性。

参考文献：

［1］丁茂实.基于运动背景的运动目标检测技术研究［D］.南京：南京航空航天大学，2009.

［2］章毓晋.图像处理［M］.北京：清华大学出版社，2006.

［3］LUCAS，B D，KANADE，T. Aniterative image registration technique with an application to stereo vision［M］. Proceedings of the DARPA Image Understanding Workshop，1988.

［4］HORN B K P，SCHUNCK B G. Determinging optical flow［J］. Artifical Intelligence，1981（17）：185-203.

Research on Fast Tracking of Moving Target in Battlefield

LI Si1，GUAN Xing-lai2，NING Jun-shuai1
（1. Ordnance Engineering College，Shijiazhuang 050003，China；
2. Chinese Luoyang Electronic Equipment Testing Center，Mengzhou 454750，China）

Abstract：Aiming at the shortcomings of HS Algorithm and LK Algorithm which the algotithm are too completed and the computing quliquanties are large. This paper brings forward Fast -speed Dirrerential Light-flow method，and verifies the feasibility of this mathod by Matlab Software.

Key words：HS algorithm，LK algorithms，light-flow mathod

作者简介：李思（1985-），男，河北辛集人，博士研究生。研究方向：军事装备学，通信技术。

*基金项目：国家自然科学基金（60904071）；军械工程学院科学研究基金资助项目（YJJXM12040）

收稿日期：2015-01-11

文章编号：1002-0640（2016）02-0004-03

中图分类号：TN924

文献标识码：A

修回日期：2015-02-25