交流感应电动机精确解耦的自抗扰控制*

钟　斌

（1.西南交通大学交通运输与物流学院，成都　610031；2.武警工程大学装备工程学院，西安　710086）



交流感应电动机精确解耦的自抗扰控制*

钟斌1，2

（1.西南交通大学交通运输与物流学院，成都610031；2.武警工程大学装备工程学院，西安710086）

摘要：为了实现交流感应电动机高性能调速，快速跟踪变化的负载转矩，对静止两相αβ坐标系中的电动机数学模型精确反馈线性化，实现转速和转子磁链系统的完全解耦。针对解耦的转速和磁链子系统的设计2个结构完全相同的自抗扰控制器，实现对转速和磁链的完全独立控制。实验研究表明：电动机转速和磁链分别大约在0.7 s和0.3 s时达到参考值；负载转矩的变化将引起转速7 rad·s-1范围内的变化，但磁链仍保持给定值；当转速稳定时，电磁转矩在1 s时间内能快速跟踪变化的负载转矩，其超调量不超过20 N·m；控制系统能适应转子电阻±10%和定子电阻+10%范围的变化。

关键词：交流感应电动机，反馈线性化，精确解耦，自抗扰控制，负载跟踪

0　引言

交流感应电动机动力学模型为高阶、强耦合、多输入、多输出非线性系统，并且电动机运行时由于温升等原因造成电动机转子电阻等参数存在不确定性，采用经典的线性控制方法难以实现输出变量的独立控制。国内外学者逐渐将Hamilton控制［1-4］、滑模控制［5-8］、无源控制［9-10］、鲁棒控制等非线性控制理论和方法应用于交流感应电动机的调速中。但这些方法仍然不能实现输出变量的解耦控制，控制的设计仍然较复杂。基于微分几何理论的非线性反馈线性比，与利用泰勒级数展开进行局部线性近似方法不同，在线性化过程中，前者并没有忽略任何高阶非线性项，所以这种线性化是精确和整体的。利用非线性反馈线性化方法，将复杂交流感应电动机模型转换为两个完全解耦的二阶线性转速子系统和磁链子系统，实现了电动机的转速系统和磁链系统的解耦控制。由于交流感应电动机参数和负载转矩存在一定的不确定性。对解耦的两个线性子系统，分别设计两个结构完全相同的自抗扰控制器使控制系统对电动机参数和负载转矩变化具有较强的鲁棒性。本文设计方法及研究结论，在交流感应电动机的高性能调速及其节能工程实际中具有明显理论价值。

1　多输入多输出仿射非线性系统模型及相对阶矢量

考虑多输入多输出（MIMO）仿射非线性系统

式中：x∈Rn，u∈Rm和y∈Rm分别为系统的n维状态变量，m维输入和输出矢量，且x=［x1x2…xn］T，u=［u1u2…um］T，y=［y1y2…ym］T；f（x）=［f1（x）f2（x）…fn（x）］T和g（x）=［g1（x）g2（x）…gm（x）］T分别为n维充分光滑的向量场，其中，fi（x）（i=1，2，…，n）为标量函数。gj（x）（j=1，2，…，m）为n维列向量；h（x）=［h1（x）h2（x）…hm（x）］T，其中hj（x）（j=1，2，…，m）为充分光滑的标量函数。

对于MIMO系统（1）中每个输出yj=hj（x）（j=1，2，…，m）有一个相应的相对阶γj，如果在x0的领域内，如有以下条件成立，γ=（γ1γ2…γm）就称为系统（1）的相对阶矢量，其中γj=（j=1，2，…，m）为相对阶数。即对于ki＜γi-1，有

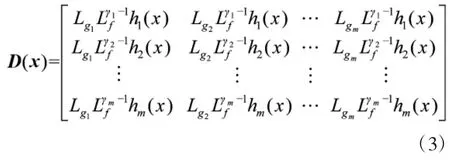
且m×m维矩阵式中：Lγm-1fhm（x）表示标量函数hm（x）对向量场

f（x）导数，即hm（x）沿f（x）方向的变化率。

2　输入-输出反馈精确线性化

由文献［11-12］，交流感应电动机在静止两相坐标系αβ中的数学模型可描述为式（1），此时式（1）中，其中ωr为转子角速度（rad·s-1），ψrα和ψrβ为转子磁链（Wb），isα和isβ为定子电流（A），，即输出。

显然，由式（2），交流感应电动机的相对阶矢量为γ=（γ1，γ2），其中γ1=γ2=2，且

在新的坐标下，感应电动机的动态方程为

显然，由式（8），前4个方程可写成

现令，虚拟控制输入为v1，v2，且

则，电机的实际控制输入为

显然，由式（8）~式（10）可以得到感应电动机的两个完全解耦的二阶线性子系统：转速子系统Ⅰ和磁链子系统Ⅱ

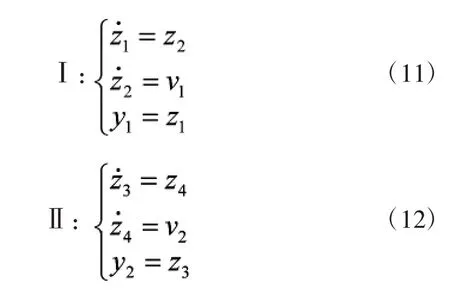
3　解耦系统的自抗扰控制

图1转速ADRC结构框图

（1）跟踪微分器：根据设定参考值安排过渡过程并提取共微分信号，其算法为

式中：r为速度因子，决定跟踪速度；h为滤波因子，决定滤波效果；T为积分步长。以x1，x2，r，h为变量的函数hfan表示成为

（2）扩张状态观测器：实现对转速子系统状态变量z1、z2的估计，并将电动机未建模动态、由于发热等原因引起的电动机参数变化及系统未知扰动扩张成新的状态变量z'3（简称扩张状态）并加以估计，其算法为

（3）误差非线性组合器：实现误差反馈的非线性组合，其算法为

转速子系统的虚拟控制输入为

采用与式（11）～式（16）同样的算法和步骤，可以设计交流感应电动机磁链ADCR，限于篇幅，不再赘述。

4　自抗扰控制系统

图2基于精确解耦的电动机自抗扰控制系统

基于精确解耦的电动机自抗扰控制系统框图如图2所示。从图中可以看出，解耦器实现电动机的精确解耦，ADCR输出转速和磁链子系统虚拟控制v1和v2逆变器根据式（10）计算电动机定子的实际控制电压usα和usβ。

5　仿真实验

电动机参数：Rs=0.082 Ω，Rr=0.05 Ω，Ls=3.44 mH，Lr=3.44 mH，np=2，J=0.37 kg·m-2。经反复实验，确定ADCR参数：转速子系统r=500，h=0.01，T=0.001，β（ESO）=［800，565，200］，β（ENC）=［3 000，26］，d=0.01，b=1；磁链子系统r=600，β（ESO）=［2 000，2 000，2 000］，β（ENC）=［1 000，100］，其余参数同转速子系统。参考值=104.7 rad·s-1=0.8 Wb2。

转速和磁链曲线如图3所示。电动机转速在约0.7 s达到参考值，磁链在约0.3 s达到参考值，两者几乎无超调现象。

图3转速和磁链曲线

电动机负载转矩跟踪及跟踪误差如图4所示。转速上升过程中，电磁转矩在约0~87 N·m范围内调节，当转速无超调地达到参考转速的同时，电动机输出电磁转矩等于负载转矩，达到了转矩跟踪的目的；负载转矩的变化将引起转速的波动，其波动范围不超过7 rad·d-1，但转子磁链仍保持不变，实现了转速和磁链的完全独立、解耦控制。

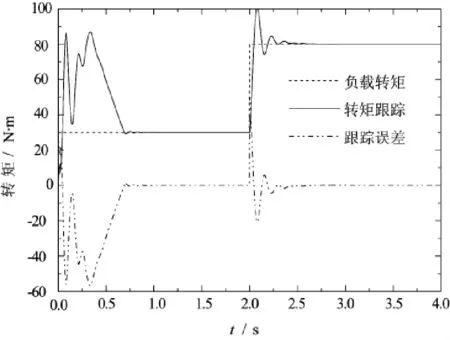
图4电磁转矩Te、负载转矩TL及跟踪误差曲线

实验还表明，所设计的控制系统能够适应电动机转子电阻±10%和定子电阻+10%范围的变化，如图5所示，显然，控制系统具有一定的鲁棒性。

图5电动机参数变化时的转速曲线

6　结论

针对交流感应电动机精确解耦的转速和磁链子系统设计的自抗扰控制器，实现了电动机以给定转速和磁链快速跟踪负载转矩的目的。通过实验研究得出了以下结论：

（1）电动机转速和磁链分别在约0.7 s和0.3 s时达到参考值；

（2）负载转矩的变化将引起转速的变化，其变化范围不超过7 rad·s-1，但磁链仍保持不变，实现了转速和磁链完全解耦控制；

（3）转速上升过程中，电磁转矩在约0~87 N·m范围内调节，当转速稳定时，电磁转矩在约1s时能够快速跟踪变化的负载转矩，其超调量不超过20 N·m。

（4）控制系统能够适应由于温度变化等原因引起的电动机转子电阻10%和定子电阻+10%范围的变化。

参考文献：

［1］裴文卉，张承慧，崔纳新，等.电动汽车用感应电机最小损耗Hamilton控制［J］.电机与控制学报，2012，16（4）：1-7.

［2］裴文卉，符晓玲，张承慧.电动汽车用感应电机动态平衡点的反馈耗散Hamilton控制［J］.控制理论与应用，2013，30（9）：1138-1144.

［3］WANG Y Z，CHENG D Z，HU X M. Problems on time-varying Hamiltonian systems：geometric structure and dissipative Hamiltonianrealization［J］.Automatica，2005，41（5）：717-723.

［4］ORETEGA R，VANDER SCHAFT A J，FERNADO C，et al. Control by interconnection and standard passivity based control of port-hamiltonian systems［J］. IEEE Transactions on Automatic control，2008，58（11）：2527 -2542.

［5］吴捷，薛峰，杨金明，等.基于滑动模控制的感应电动机增益自适应锁相环速度控制［J］.电工技术学报，2000，15 （2）：54-60.

［6］韩亚军，杨小强，祝万平，等.基于滑模变结构的感应电动机直接转矩控制［J］.工矿自动化，2012，（8）：71-74.

［7］王家军.基于自回归小波神经网络的感应电动机滑模反推控制［J］.自动化学报，2009，35（1）：1-8.

［8］史宏宇，冯勇，张袅娜.感应电动机全局高阶滑模观测器［J］.吉林大学学报（工学版），2013，43（30）：688-694.

［9］FUJIMOTO K，SAKURAMA K，SUGIE T. Trajectory tracking control of port controlled hamiltonian systems via generalized canonical transformations［J］. Automatica，2003，39（12）：2059-2069.

［10］AKRAD A，HILAIRET M，ORETGA R，et al. Interconnection and damping assignment approach for reliable PM synchronous motor control［C］//IET Colloquium on Reliability in Electromagnetic systems. Paris：Institution of Engineering and Technology，2007.

［11］马莉丽、程文明、钟斌.起重机电机拖动系统负载跟踪控制研究［J］.西南交通大学学报，2013，48（3）：494-499.

［12］王家军，马国进.基于Petri模糊神经网络磁通观测器的感应电动机无速度传感器控制［J］.控制理论与应用，2010，27（9）：1195-1200.

AC Asynchronous Motor’s Active Disturbance Rejection Control Based on Precise Decoupling

ZHONG Bin1，2
（1. School of Transportation and Logistics，Southwest Jiaotong University，Chengdu 610031，China；
2. Equipment Engineering College，Engineering University of Chinese Armed Police Force，Xi’an 710086，China）

Abstract：In order to realize AC asynchronous motor’s high performance speed regulation，changing load torque’s fast tracking，the motor’s mathematical model of static two-phase coordinate system αβ is precisely linearized，and realized full decoupling of rotate speed system and rotor flux linkage system. Two active disturbances rejection controllers are designed flux linkage system，and for decoupled rotate speed system and rotor fully independently rotate speed and flux linkage are controlled. Experiment results show：rotate speed reached reference value about 0.7 s，and flux linkage reached reference value about 0.3 s；load toque’s changing would cause rotate speed’s changing about 7 rad·s-1，but flux linkage still held at reference value; the electric torque could fast track changing load torque in 1s when rotate speed is stabilized and electric torque’s overshoot doas not exceed 20 N·m；the designed control system an be adapted variation range of±10%rotor resistance and +10% stator resistance.

Key words：AC asynchronous motor，feedback linearization，precise decoupling，active disturbance rejection control，load’s tracking

作者简介：钟斌（1975-），男，四川万源人，博士，副教授，硕士生导师。研究方向：机电系统智能控制及自动化，军事装备理论及技术。

*基金项目：国家自然科学基金资助项目（51005246）

收稿日期：2015-01-08

文章编号：1002-0640（2016）02-0023-05

中图分类号：TM341

文献标识码：A

修回日期：2015-03-01