高中地理教学与数学的交叉融合

郑丙沛 杨晓英（贵州师范大学 地理与环境科学学院, 贵州 贵阳 550001）



高中地理教学与数学的交叉融合

郑丙沛 杨晓英
（贵州师范大学 地理与环境科学学院, 贵州 贵阳 550001）

摘要：地理与数学之间具有密切的学科相关性，两门学科的交叉融合能够有效增强高中地理教学活动的科学性、高效性和趣味性。新高考改革背景下，实施高中地理与数学的交叉融合教学可从数学思想、数学方法、数学工具、数学能力等四个方面入手。

关键词：地理；数学；交叉融合；教学

2017年，新高考改革方案将在全国范围内实施。新方案取消了文理分科，规定语文、数学、外语为统考学科，地理、政治、历史、物理、化学、生物等为自选等级考试学科，考生可自选其中三门进行考试并将最好成绩计入高考总成绩。在此背景下，地理作为“文科中的理科”，因其学科的特殊性势必会成为不同文理倾向学生争相选考的热点。这对地理教学和学科发展而言，既是新的挑战，又是难得的发展机遇。

地理学是一门兼有自然科学和人文社会科学性质的综合性学科[1]，这在一定程度上决定了高中地理课程与作为“一切自然科学的基础”的数学之间具有密切的联系。因此，实施地理与数学的交叉融合教学是地理学科性质使然。地理与数学的交叉融合教学不是将地理与数学知识进行简单机械地罗列和对照，而是在大科学观指导下，以地理课程和地理教学为主体，将数学中最精髓的部分渗透到高中地理教学活动，最终达到丰富教学内容、提升学习效率、突破学科思维定式和贯通学科横向联系的目的。将数学与地理教学活动相融合的形式，不仅能锻炼和提升偏文科学生的抽象思维与空间想象能力，还有利于为偏理科学生搭建起重新认识和学习地理课程的桥梁，这对于弥补新方案带来的竞争差距和促进学生的综合发展具有非常重要的意义。

高中地理与数学间的交叉融合教学并没有固定的模式和套路，一般可从数学思想、数学方法、数学工具和数学能力四个方面开展。

一、高中地理与数学思想的交叉融合

数学思想作为数学思维的结晶，是人类对现实世界的数量关系和空间结构的理性认识。数学思想作为数学最精髓的部分，具有内容丰富、应用广泛的特点。在高中阶段，很多地理知识内容的讲授和学习都会用到数学思想，而在众多数学思想中，以数形结合思想、集合思想、函数思想和整体思想的使用频率最高。

1.数形结合思想

根据数字与图形之间内在的对应关系，通过相互转化的形式来表达两者之间关系的思想就是数形结合思想。在地理教学活动中使用数形结合思想，能够以数字和图形相结合的直观形式呈现地理现象的变化和规律，使复杂的地理现象简单化，能有效提升授课和学习效率[2]。例如，在揭示到达大气上界的太阳辐射与地球纬度间的关系时，可利用数形结合思想来引导学生进行研究学习。太阳年辐射总量与纬度之间存在一定的相关关系，但究竟是怎样的关系呢？这可以借助“北半球大气上界太阳辐射分布图”（见图1）中的图形与数字间的对应关系来找出答案。图1中，横轴表示北半球各地纬度，纵轴表示年总辐射量的变化。从0°到90°N虽然纬度不断升高，但所对应的柱状条纹高度却逐级递减，所示年总辐射量数值也由约13×109J/m2递减为约6×109J/m2，由此可见太阳年总辐射量与纬度值之间呈负相关关系，即到达大气上界的太阳辐射因纬度的升高而减少。

数形结合思想在高中地理中应用的案例还有很多，如地震波传播速度分异、气温和降水类型分异、雪线高度差异、全球气候演变周期、城市化进程、世界水资源分布等。

图1 北半球大气上界太阳辐射分布图

2.集合思想

集合思想是指将具有某种特定性质的具体或抽象对象汇集为整体的一种思想。虽然这是数学领域的一个概念，但这一思想却在高中地理课程中广泛使用，特别是在地理事物的关系表述和层次划分方面。例如，在学习自然灾害系统时，可以借助集合间的包含、并列和交叉关系来表述孕灾环境、致灾因子、承灾体和灾情之间的复杂关系（见图2）。由图2可知，自然灾害系统由孕灾环境、致灾因子、承灾体和灾情四要素构成，四者之间的关系为：在孕灾环境这一大集合中包含致灾因子、承灾体两个小集合，其中孕灾环境中致灾因子集合与承灾体集合的交集部分就是灾情，即自然灾害的灾情取决于孕灾环境、致灾因子和承灾体三者的共同作用。

类似的集合思想应用案例还有很多，如天体系统层次划分、资源类型划分、气候类型划分、河流补给类型划分、能源类型划分、农业地域类型划分等。

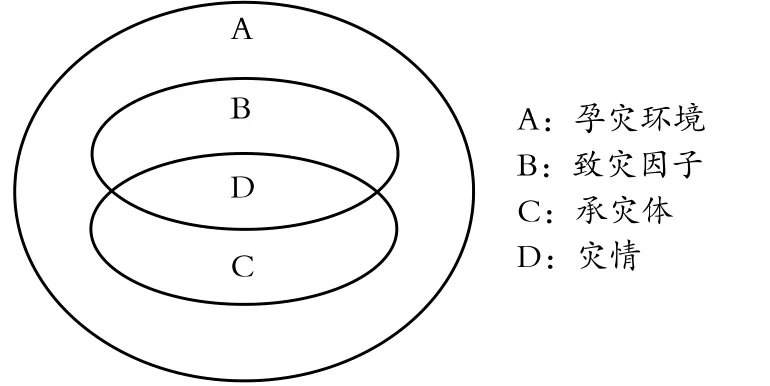
图2 自然灾害系统结构图

3.函数思想

函数是一种对自然界中量的依存关系的描述，即一个事物随另一个事物变化而变化的关系和规律。借助函数思想可以更加准确地把握两个地理事物间的相对关系。以指数函数为例，在学习“世界人口变化情况”内容时，通过观察“工业革命以来的世界人口变化情况图”（见图3），可以发现该图像近似于y=ax(a>1) (x∈R)的指数函数图像，因此可以借用指数函数性质来认识世界人口数量变化情况。因为y=ax(x∈R)中，a>1，所以该函数为单调递增型指数函数，结合图像可知工业革命以来的世界人口数量呈递增状态，且二战前后的增长速度存在很大差异。同时，根据指数函数单调性还可以预判出世界人口数量在未来一段时间仍会继续增长这一趋势。借助函数思想，从数学视角来理解不同变量间的依存关系，不仅能加深学生对该知识点的认识和理解，而且还有利于增强课程的科学性、严谨性，培养学生的探究意识[3]。

类似的函数思想应用案例还有很多，如气温的日变化曲线、大洋表层海水盐度曲线、温度与纬度关系曲线、城市化进程曲线等。

图3 工业革命以来的世界人口变化情况图

4.整体思想

整体是与部分相对应的一个概念。整体思想强调问题的整体性，包括把握问题的整体结构性和相互关联性，并以整体、综合的视角审视和处理问题。整体性是自然地理环境最基本的特征，也是高中地理教材中蕴含的重要思想之一。不管是地理要素间的物质与能量交换、地理要素间的相互作用、自然地理环境演化过程这些小的知识点，还是人口变化、城市化、工业发展、农业发展、交通布局、旅游开发、生态保护、自然灾害防治这些大的单元模块，都能体现出浓郁的“牵一发而动全身”的整体思想。另外，在整体思想指导下，正确把握人口、资源、环境与发展之间的关系，也是历年高考考查的重点。因此，立足于整体思想，把握地理环境的整体性，是学好、用好地理知识的一大关键。

二、高中地理与数学方法的交叉融合

以数学语言来表述事物的状态、关系和过程，并加以推导、演算和分析，最终形成对问题的判断、解释和预言的方法称之为数学方法。在高中地理教学活动中，经常使用的数学方法有作图法、穷举法、公式法和比较法。

1.作图法

高中阶段，很多地理知识点和题型都需要借助作图法进行理解和解答，有的题型甚至直接要求作图，例如“大气运动”中的风向判定问题。这类题目通常会直接或间接告知某地点所在纬度（半球）、气压数值和海拔高度等关键信息。解答该类题型，多借助作图法，根据已知的关键信息分四步完成。首先，要根据气压值确定气压梯度，并在此基础上画出水平气压梯度力，方向为垂直于等压线，由高压指向低压。其次，结合题中所给纬度信息，判断出地转偏向力的方向。然后，根据所在地海拔高度，确认是否受摩擦力影响。最后，在水平气压梯度力的辅助下，结合纬度和摩擦力信息最终确认并标示出风向。

作图法除了用于风向判定外，还被广泛应用于锋面运动、气旋性质、河流流向、洋流运动方向等问题的判定。同时，在工业布局、交通布局、城市规划、旅游规划、港址选择、自然灾害防治等内容也经常会间接或直接用到作图法。

2.穷举法

穷举法，又称枚举法，一定意义上也可以理解为代入法或分类讨论法。该方法在地理试题解答中运用较多。地理试题中有一些类似数学中分类讨论的试题，解决这类题型必须进行分类讨论才能得出答案。

例如，不同半球的港口选址问题。“已知中纬度某河流沿岸有A、B两城镇（见图4），两城镇的自然条件和社会经济条件无异，箭头方向为河流流向，那么A、B两地哪里最适合修建码头？”由题可知，该地位于中纬度地区，A、B两地位置接近，自然条件、社会经济条件无异。因此，在高中阶段这种情况下码头选址只需考虑地转偏向力因素，分为以下两种情况。

(1)若河流位于北半球，受地转偏向力影响，B地所在河岸受侵蚀较强，泥沙易在A地所在河岸沉积，因而码头宜建在B地。

(2)若河流位于南半球，受地转偏向力影响，A地所在河岸受侵蚀较强，泥沙易在B地所在河岸沉积，因而码头宜建在A地。

图4 A、B两城镇沿河分布图

3.公式法

公式法可理解为公式计算法，即利用公式和已知条件进行数学运算。在高中地理中，公式计算题型较为常见。例如，利用公式求正午太阳高度。正午太阳高度计算公式为：H=90°-|Φ-δ|。其中，Φ为当地纬度，δ为太阳直射点的地理纬度（夏半年为正值，冬半年为负值）。因此，求某地正午太阳高度，只需将当地纬度和太阳直射点纬度代入正午太阳高度计算公式即可。

高中阶段，常用的地理计算公式还有比例尺公式、经纬度距离公式、绝对高度公式、相对高度公式、坡度公式、人口出生率公式、人口死亡率公式、人口自然增长率公式、人口密度公式、城市化水平公式、原料指数公式及各类产值计算公式等。

4.比较法

比较法是地理学中进行案例研究常用的方法。在高中地理课程中，很多教材内容的设置都采取了对比展开的形式，特别是区域地理模块。如“荒漠化防治”一节中，将我国西北地区与非洲萨赫勒地区、苏联垦荒区进行了对比；“森林开发与保护”中，将亚马孙雨林与我国西双版纳、三江平原进行了对比；“流域综合开发”中，将田纳西河流域与墨累-达令河流域、中国红水河流域进行了对比；“区域工业化与城市化”中，将“珠三角”地区与“长三角”地区进行了对比等。通过这种案例集中对比的形式，不仅可以做到集中学习、加深印象，而且还能拓展学生的发散思维，引导他们关注不同模块间的横向联系和建立纵向知识体系框架，因而具有很强的实用价值。

三、高中地理与数学工具的交叉融合

数学工具作为一种教学辅助手段，具有很强的实用性，因而也经常用来辅助地理教学和学习。高中地理中，常用的数学工具有数轴、坐标系、数学模型、数学图形等。

1.数轴

高中地理课程相对于初中地理而言，在知识体系上变得更加细化和深入，学习难度也有所提升，尤其是在地理数据的识记与运用方面。当面对大量的地理数据时，很多人倾向于采取传统“死记硬背”的形式，这样不但浪费时间，而且会经常遗忘或出错。这时候如果恰当地运用数轴，就可以减少这种状况的发生。例如：在农作物熟制和农作物分异知识环节，根据活动积温的不同可以将我国划分为赤道带（>10000℃）、热带（8000~10000℃）、亚热带（4500~10000℃）、暖温带（3400~4500℃）、中温带（1600~4500℃）、寒温带（<1600℃）等6个温度带和青藏高原区。借助数轴进行区分和记忆（见图5），可以避免记忆繁多的数字区间，学生只需要记住1600、3400、4500、8000、10000五个数值和一个特殊地区，然后在数轴上稍作区分即可。这样记忆不仅形式简单、记忆量小，而且操作方便、不易出错。

除此之外，利用数轴工具进行数值记忆或处理的方法，还可以广泛应用于时区计算、大气垂直分层、等降水量线、等温线、等高线、等潜水位线、等深线、等压线、等震线、等盐度线、等pH值线、等太阳辐射线、太阳辐射光谱、城市等级划分等处。

图5 积温带数值划分图

2.坐标系

在高中地理中，常用的坐标系有平面直角坐标系、平面正三角形坐标系和平面正方形坐标系等。其中，以平面直角坐标系最为常见。平面直角坐标系是在数轴的基础上发展起来的，通常由两条数轴的垂直叠加构成，可以用于研究两个地理要素间的关系。例如，在研究城市内部空间结构时，用来研究地租水平和距市中心距离两者之间的关系。地租水平和距市中心距离间的关系仅从文字理解比较抽象，但如果借助平面直角坐标系就会简单很多。如“各类土地利用付租能力随距离递减示意图”（见图6）所示，距市中心越近地租水平越高，商业、住宅、工业三种活动的付租能力各不相同，由强到弱依次为商业、住宅和工业，因此付租能力最高的商业区分布于距市中心最近的A区，付租能力次之的住宅区分布于距市中心较近的B区，付租能力最低的工业区分布于距市中心最远的C区。

除此之外，平面直角坐标系还可以应用在太阳黑子数变化、气候变迁、人口数量变化、人口增长模式及转变、城市化进程、土壤肥力变化等知识点。

图6 各类土地利用付租能力随距离递减示意图

3.数学模型

数学模型简言之就是用数学语言表示的一种抽象、简化的模型结构。其种类有很多，但在高中地理中以几何模型最为常见。例如，在学习不同等级城市服务功能时，会涉及到克里斯泰勒的“中心地理论”。教材中关于这一理论的文字介绍虽然不多，但对于高中阶段的学生而言，理解起来仍有一定困难。此时如果借助“城市服务范围嵌套模型”——六边形嵌套模型，就能相对形象直观地理解和描绘出不同城市等级空间分布规律了。

高中阶段，类似的数学模型应用案例还有地球模型、城市地域结构模型、杜能同心圆模型、韦伯区位三角形模型、灾害系统要素关系模型等。

4.数学图形

数学图形按照内容分类可分为函数图形、几何图形，按照形态分类可分为平面图形和空间图形。在高中地理中，对于数学图形的使用并不需要作严格区分，也不需要过于苛求精确，很多时候只需要“借其形，显其意”即可。例如，“借正弦函数之形，显褶皱之意”。褶皱是在地壳运动作用下岩层发生波浪状的塑性形变。褶皱的基本单位为褶曲，一个褶曲包括一个背斜和一个向斜。背斜岩层一般为向上拱起，向斜岩层一般为向下弯曲（背斜谷、向斜山除外）。此时，在描述褶曲这一概念时，可以借用学生已有知识储备y=sinx的正弦曲线来进行形象解释。将褶皱的一个褶曲理解为正弦曲线的一个周期（2π），将背斜、向斜分别对应正弦曲线的前、后半个周期（π），以知识迁移的形式实现对褶皱的认识与学习。如此一来不仅简化了新知识点的学习过程，又体现出了地理课程的趣味性，效果非常显著。

数学图形在高中地理中的应用还有很多。例如，利用三角函数曲线解释太阳直射点的回归运动轨迹，根据不同需要将地球视作圆形、半球体、正球体、椭圆等图形来认识地球、理解概念或解题，将大洲轮廓简化为几何图形去识记大洲、洋流、气候类型等，以及运用扇形图、饼图、柱状图等统计图形进行概念理解和数值表示等。

四、高中地理与数学能力的交叉融合

数学能力是在数学活动中发展并表现出来的一种个性心理特征和潜能，也是人类所必须具备的一种重要能力。一般认为，数学能力包括抽象概括能力、逻辑推理能力、空间想象能力和数学运算能力[4]，这些能力也是地理学习和实践中不可或缺的。

1.抽象概括能力

抽象概括能力作为一种数学思维能力，是指能在纷繁的数据或文字中，根据各类现象间的内在联系，分离出问题的核心和实质，并把具体问题抽象概括为数学模型的能力[5]。抽象概括能力是分析和解答地理试题的基础，也是各类考试考查的重点。图形题和图文材料题是对学生抽象概括能力最直接的考查形式。形式多样的各类统计图、区域图、分布图、等值线图、景观图、示意图，配以大段的文字材料，使得题目的难度迅速提升，也对学生的抽象概括能力提出了更高要求。要想快速解决此类题型，必须能够迅速分析文字及图表，提取有效信息，然后进行总结概括，将题目中零散、抽象的信息进行条理化、文字化处理，最终形成所需的答案。因此，可以说良好的抽象概括能力是学好地理课程的基础。

2.逻辑推理能力

逻辑推理是从一般性的前提出发，通过合理思考和科学选择，得出相应结论或判断的过程。根据推理过程的思维方向，可将逻辑推理划分为演绎推理、归纳推理和类比推理三类。其中，演绎推理是指由一般到特殊的推理。例如，由长江中下游地区为亚热带季风气候，上海、南京、武汉位于长江中下游地区，可知上海、南京、武汉等地都为亚热带季风气候。归纳推理多指由特殊到一般的推理。例如，已知太平洋中分布有矿产资源，大西洋中分布有矿产资源，印度洋中分布有矿产资源，北冰洋中分布有矿产资源，而太平洋、大西洋、印度洋、北冰洋为地球上的全部大洋，那么可知地球上的全部大洋都有矿产资源。类比推理是由特殊到特殊的推理。例如，地球进行公转和自转，并且存在昼夜交替现象；月球也进行公转和自转，那么可知月球也有相应的昼夜交替现象。可见，具备一定的逻辑推理能力对于形成地理思维和拓展地理知识具有非常重要的意义。

3.空间想象能力

空间想象能力是人类在对客观事物的空间形式进行观察、分析和实践基础上，获得的一种可以对物体形状、结构及位置进行思考的能力。高中地理一直以来被认为是“文科中的理科”，对学生的空间想象能力要求较高，尤其是在必修1和选修1模块中。例如，地球运动、黄赤交角、回归运动、周日运动、地图投影、球面运动、天球及天球坐标、月球运动、日月会合运动等诸多抽象知识点，需要借助学生空间想象才能得以真正理解和运用。另外，空间想象能力在进行地理解题过程中也同样重要。解答地理问题时，要能根据题中的信息在脑海中迅速构建起地理模型，并将一维的文字、二维图像进行匹配和三维重构，然后在此基础上结合所学知识和模型性质完成答题，这期间绝对离不开空间想象能力的支持。

4.数学运算能力

数学运算能力主要是指在一定数学概念、法则、定理或规律指导下进行相关数学运算的能力[6]。运算能力作为最基本的数学能力，也是地理学习和实践中必须具备的能力，这点在地理课程学习和高考试题中都有体现。例如，等值线判读、正午太阳高度计算、时间计算、距离计算、温度计算、高度计算、人口变化计算、城市化水平计算及其他计算等很多地方都会用到数学计算，都是在考查学生的数学运算能力。学生数学运算能力的强弱将关乎计算的速度和准确性，进而影响到学习和答题进度。因此，不断夯实运算基础，增强数学运算能力，是高中地理课程的必然要求。

参考文献：

[1] 郑度,杨勤业.中国现代地理学研究与前瞻[J].科学,2015(04):29-30.

[2] 李晴.试论地理案例教学[J].中学地理教学参考,2001(09):4-5.

[3] 徐蓉.浅谈中学地理在素质教育中的作用[J].贵州师范大学学报(自然科学版),1998(01):117-118.

[4] 代文军,蔡惠萍.论学生数学能力的培养[J].石家庄职业技术学院学报,2009(12):49-50.

[5] 曲晓春.数学抽象概括能力的培养[J].现代交际,2010(12):172.

[6] 中华人民共和国教育部.义务教育数学课程标准（2011年版)[S].北京:北京师范大学出版社,2012.