基于RBF的电液变量施肥控制系统PID参数整定
呼云龙,孙 萌,梁春英,王 熙
(黑龙江八一农垦大学 信息技术学院,黑龙江 大庆 163319)
基于RBF的电液变量施肥控制系统PID参数整定
呼云龙,孙萌,梁春英,王熙
(黑龙江八一农垦大学 信息技术学院,黑龙江 大庆163319)
摘要:电液变量施肥控制系统的非线性和PID算法的局限性,导致常规PID控制已不能满足控制系统性能要求。为此,提出了基于RBF神经网络整定PID参数的方法,利用自适应RBF神经网络辨识被控对象Jacobian信息,采用梯度下降法计算PID参数Δkp、Δki、Δkd,对系统进行增量式PID控制。与采用增量式PID的系统阶跃响应曲线对比可知,利用RBF-PID算法的系统具有良好的动态性能及较强的自适应性。
关键词:变量施肥;径向基神经网络;PID参数整定
0引言
21世纪以来,在变量施肥技术方面,国内外已经取得丰硕的研究成果[1-2],但是变量施肥控制策略方面的研究比较罕见,且控制系统多采用PID控制。液压控制系统的非线性和常规PID控制策略的局限性,导致变量施肥控制系统自适应性能不足,而智能控制理论的发展为解决这一问题提供了新方法。古玉雪等[3]应用模糊控制有效地解决了开度转速双变量施肥控制系统中车载电脑运算能力与施肥精度之间的矛盾。孙裔鑫等[4-6]将模糊控制、遗传算法、BP神经网络应用于PID参数整定,减小了系统超调量、缩短了调节时间、增强了系统自适应能力、提高了系统施肥精度。
相比多层前馈网络,RBF神经网络结构简单、具有良好的泛化能力,能够以任意精度逼近任意非线性函数。将RBF神经网络应用于参数变化的被控系统PID参数整定中,可以有效提高系统动态性能和稳定性、增强系统自适应性能。为此,本文针对电液变量施肥控制系统,利用RBF神经网络整定PID参数。
1阀控液压马达系统数学建模
1.1控制系统组成
电液变量施肥控制系统由变量施肥控制器、比例放大器及液压马达等组成,如图1所示。

图1 系统组成原理框图
1.2电液比例方向阀数学建模
系统采用博世力士乐4WRE6V16-2X/G24型直动式电液比例方向阀,可将其视为二阶振荡环节,有
(1)
式中ωv—阀的无阻尼自振频率;
ξv—阀的阻尼系数。
1.3阀控液压马达数学建模
系统采用BM3-80摆线液压马达。系统通过输入的负载流量控制液压马达的转速。
1.3.1阀的线性化流量方程
线性化流量方程为
QL(s)=KqXv(s)+KcPL(s)
(2)
式中Kq—稳态工作点附近的流量增益;
Kc—阀的流量-压力系数;
PL—负载压力。
1.3.2液压马达的流量连续方程
流量连续方程为
(3)
式中ω—液压马达输出的角速度;
Dm—液压马达的排量;
Ctm—液压马达总的泄漏系数;
βe—油液弹性模量。
1.3.3液压马达的力矩平衡方程
力矩平衡方程为
(4)
式中Jt—系统的转动惯量;
G—负载的扭转弹簧刚度;
Bm—负载和液压马达的黏性阻尼系数;
TL—负载力矩。
根据式(1)、式(2)、式(3)、式(4)得到阀控液压马达系统模型如图2所示。

图2 阀控液压马达系统模型
1.4系统开环传递函数
由图2可知,系统输出转速的反馈电压与输入偏差电压的开环传递函数为
(5)
式中Km—转速-电压反馈系数。则有
1.5系统参数
根据液压器件的电子样本、液压手册及液压实验台资料可查得系统参数如表1所示。
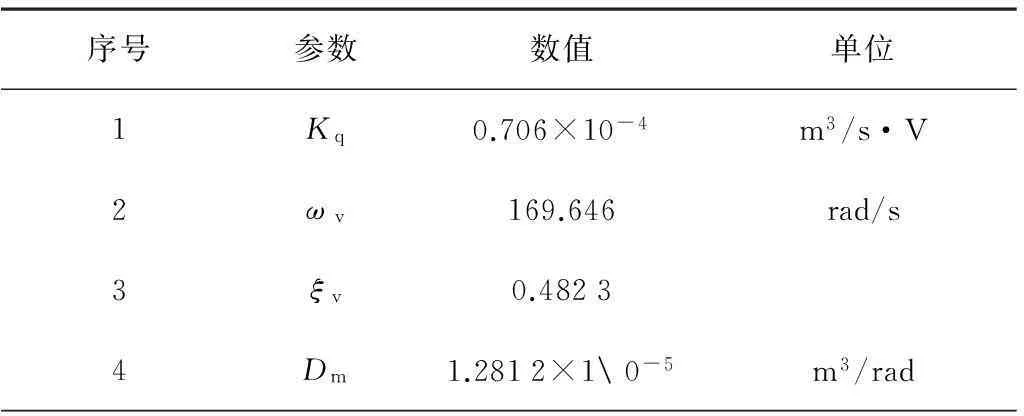
表1 系统技术参数

续表1
2增量式PID控制及参数整定
2.1增量式PID控制算法
为了避免传感器故障引起的执行机构位置大幅变化,系统采用增量式PID控制。
增量式PID控制算法为
Δu(k)=kp[error(k)-error(k-1))+kierror(k)+
kd(error(k)-2error(k-1)+error(k-2)]
(6)
式中Δu(k)=u(k)-u(k-1)
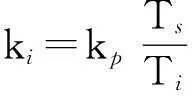
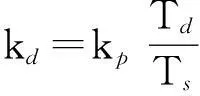
kp—比例系数;
error(k)—控制偏差量;
u(k)—PID输出。
2.2Ziegler-Nichols PID参数整定
将式(5)离散化后进行Z变换得到被控对象的差分方程为
y(k)=3.132y(k-1)-3.74y(k-2)+2.032y(k-3) -
0.428 8y(k-4)+0.000 278 8u(k-1)+
0.002 571u(k-2)+0.002 169u(k-3)+
0.000 1677u(k-4)
(7)
应用MatLab提供的margin()函数求得系统的剪切频率kc=1.984 8°,幅值裕度wc=259.691rad/s,可以求得系统的周期Tc= 2π/wc=0.024 2s。根据表2给出的Zigler-Nichols整定公式可知:kp=1.190 9、Ti=0.012 1、Td=0.003 0。取系统采样时间Ts=1ms,求得ki=0.098 4、kd=3.601 6。

表2 Zigler-Nichols
将已整定的PID参数带入增量式PID的公式中,并对式(7)进行增量式PID控制,系统的阶跃响应如图3所示。因此,系统时域性能指标为超调量σp1=29.47%、峰值时间tp1=0.016s、调节时间ts1=0.135s、上升时间tr1=0.012s、延迟时间td1=0.002s、振荡次数N=5。

图3 增量式PID阶跃响应曲线
3RBF-PID
3.1RBF神经网络的PID整定原理
基于RBF神经网络的PID控制器可以分为两个部分:
1)PID控制器。通过改变PID参数的增量的方式在线调节kp、ki、kd,对被控对象进行增量式PID控制。
2)RBF神经网络。根据系统运行状态,通过梯度下降法计算输出权值、节点中心及节点宽度,辨识被控对象Jacobian信息,根据梯度下降法计算出Δkp、Δki、Δkd。
3.2RBF辨识网络模型
RBF神经网络是一种具有局部逼近能力的三层前馈型神经网络,研究表明:RBF神经网络可以以任意精度逼近任意连续函数。
隐藏层的输出由高斯基函数构成,有
其中,bj表示高斯基函数的节点宽度B=[b1,b2,b3,…,bm]T;X=[x1,x2,…,xn]T为网络的输入变量;Cj为第j个节点的中心矢量Cj=[cj1,cj2,…,cjn]T。
RBF辨识网络的输出为
辨识器的性能指标函数为
根据梯度下降法对输出权值,节点中心及节点宽度的调节如下
bj(k)=
bj(k-1)+ηΔbj+α[bj(k-1)-bj(k-2)]
cji(k)=
cji(k-1)+ηΔcji+α[cji(k-1)-cji(k-2)]
式中η—学习率;
α—动量因子。
3.3Jacobian信息辨识
其中,x1=Δu(k)。
3.4PID参数调节
RBF神经网络的整定指标为

kp、ki、kd的调整采用梯度下降法,有
其中,xc(1)=error(k)-error(k-1),xc(2)=error(k),xc(3)=error(k)-2error(k-1)+error(k-2)
3.5RBF-PID算法
RBF整定PID控制系统的结构如图4所示。该控制器的算法归纳如下:
1)确定RBF网络的结构,并给出网络的初始节点中心cj、输出权值wj、节点宽度bj,选定学习率η和动量因子α。
2)采样得到u(k)、yout(k)、ym(k),计算该时刻误差yout(k)-ym(k)。
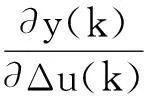
4)采用梯度下降法计算Δkp、Δki、Δkd,调整kp、ki、kd,根据增量PID公式计算PID控制器的输出u(k)。
5)更新参数,转到步骤2),进行新一轮学习,实现PID控制器的自适应调整。
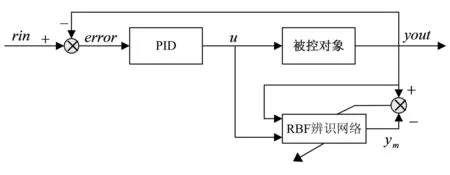
图4 RBF网络整定PID控制框图
3.6RBF-PID仿真分析
被控对象为式(7),RBF辨识网络结构选用3-6-1,网络辨识的输入为Δu(k)、yout(k)、yout(k-1),学习率η=0.01、动量因子α=0.01,输入信号rin(k)=1.0。系统的阶跃响应曲线如图5所示。
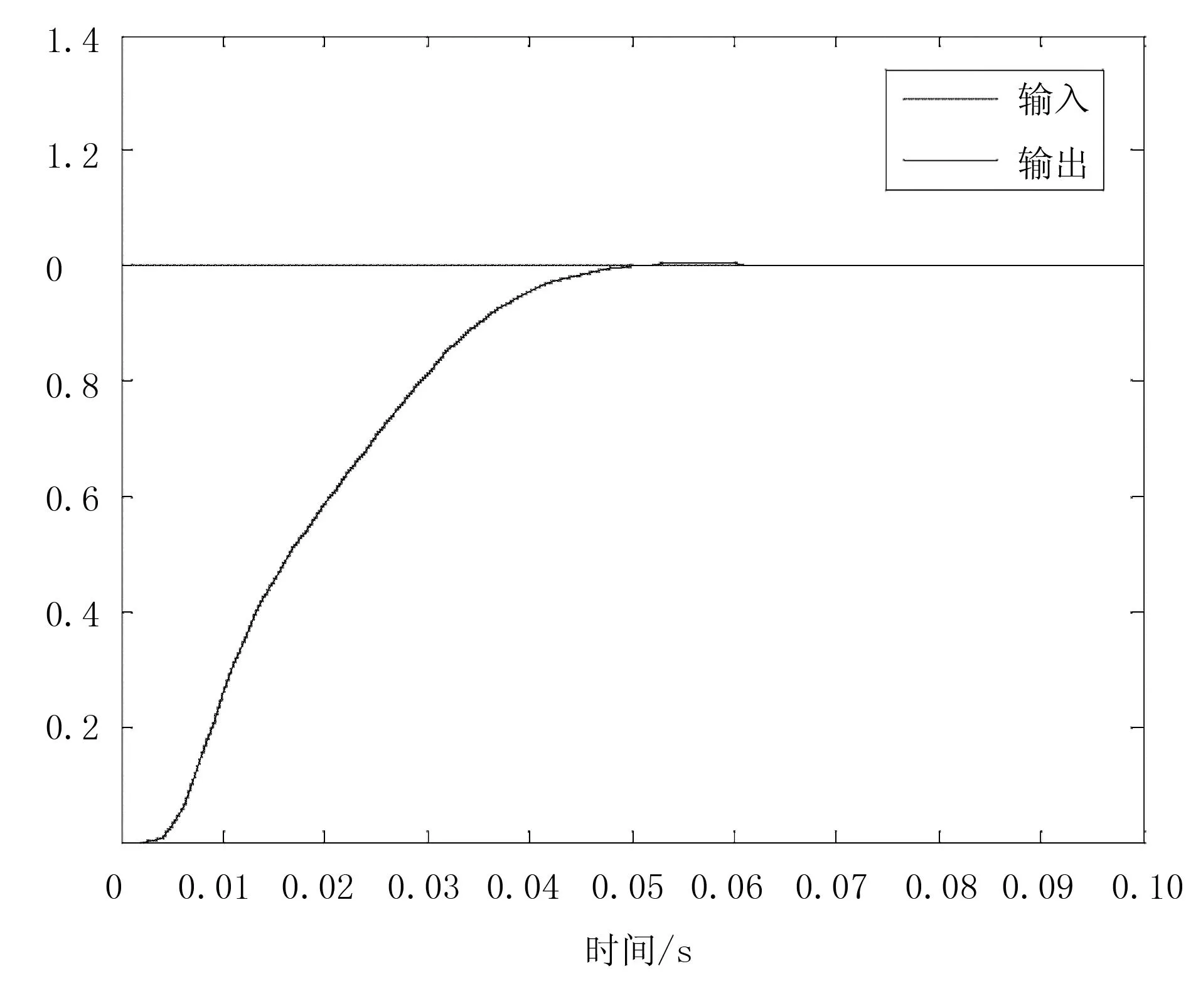
图5 RBF-PID阶跃响应曲线
系统时域性能指标为:超调量σp2=0.038%、峰值时间tp2=0.056s、调节时间ts2=0.064s、上升时间tr2=0.05s、延迟时间td2=0.002s、振荡次数N=1。系统的参数kp、ki、kd自整定曲线如图6所示。
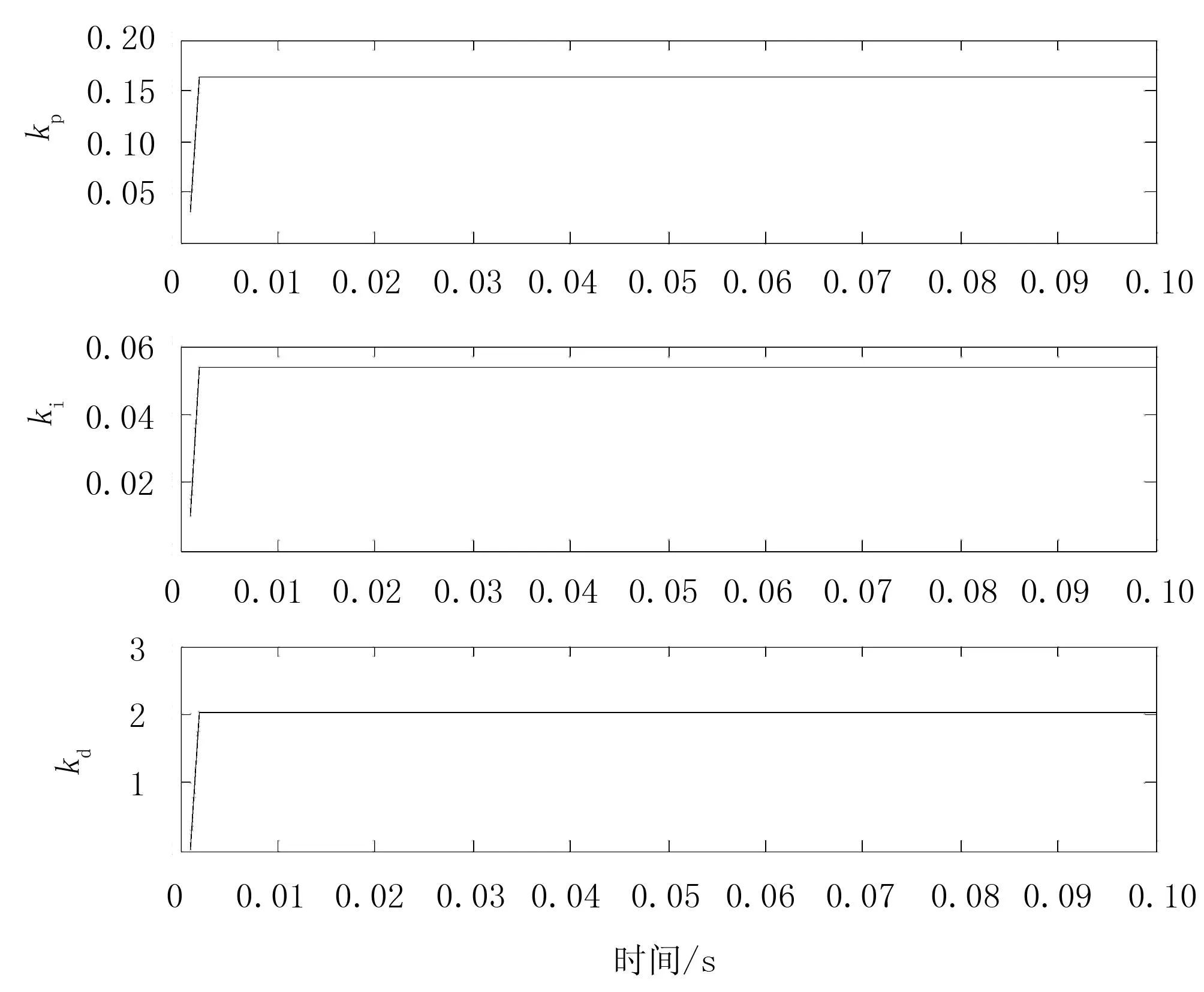
图6 RBF-PID参数自整定曲线
4结论
1)由图3、图5可知:RBF-PID算法比增量式PID算法有更好的时域性能,系统的调节时间很短、几乎没有超调量。
2)由图6可知:RBF-PID算法可以迅速地找到合适的PID参数,使系统更快地达到稳态。
3)电液比例变量施肥控制系统是非线性系统,当系统参数发生变化时,常规PID控制系统很容易发生振荡、产生较大的超调量,使系统很难在较短的时间内达到最优的控制效果;RBF-PID控制系统由于PID参数在线整定,能够很快地适应系统参数变化,从而很快地跟踪系统给定值。
参考文献:
[1]伟利国,张小超,苑严伟,等.2F-6-BP1 型变量配肥施肥机的研制与试验[J].农业工程学报,2012,28(7):14-18.
[2]Tajudeen A I, Azmi Y, AbdulRashid M S, et al. Effects of operational variables on rotary valve metering system for a variable rate technology fertilizer applicator for oil palm[J].Journal Applied Sciences,2013,13 (3):479-484.
[3]古玉雪,苑进,刘成良.基于模糊系统的开度转速双变量施肥控制序列生成方法[J].农业工程学报,2011,21(11):134-139.
[2]孙裔鑫,梁春英,王熙.基于模糊PID的变量施用颗粒肥控制算法的研究[J].安徽农业科学,2011,39(12):7435-7436.
[4]梁春英,吕鹏,纪建伟,等.模糊自整定PID算法在CVT变量施肥系统中的应用[J].沈阳农业大学学报,2013,44(4):461-466.
[5]梁春英,吕鹏,纪建伟,等.基于遗传算法的电液变量施肥控制系统PID参数优化[J].农业机械学报,2013,44(Sup1):88-93.
[6]张怡卓,刘步玉,马琳. BP-PID控制方法在变量施肥控制系统中的应用[J].现代电子技术,2012,35(5):192-194.
PID Parameter Setting of Electro-hydraulic Variable Rate Fertilization System Based on RBF
Hu Yunlong, Sun Meng, Liang Chunying,Wang Xi
(College of Information and Technology,Heilongjiang August First Land Reclamation University, Daqing 163319, China)
Abstract:Nonlinearity of electro-hydraulic variable rate fertilization system and limitations of PID algorithm lead that normal PID control cannot meet the performance requirements of control system. Aimed at this, a method of setting PID parameter based on RBF neural network has been proposed, which takes advantage of adaptive radial basis function neural network (ARBFNN) to identify the Jacobian information of controlled object, adopts gradient descent to calculate PID parameters Δkp,Δki,Δkd,and conducts incremental PID control on system. Compared with the step response curves of incremental PID algorithms, it can be learnt that the system which adopts RBF-PID algorithm has excellent dynamic performance and strong adaptivity.
Key words:variable rate fertilization; radial basis function neural network (RBFNN); PID parameter setting
文章编号:1003-188X(2016)03-0014-05
中图分类号:S224.2;S237
文献标识码:A
作者简介:呼云龙(1987-),男,哈尔滨人,硕士研究生,(E-mail)649196684@qq.com。通讯作者:梁春英(1971-),女,山东商河人,教授,博士,(E-mail)ndliangchunying@163.com。
基金项目:“十二五”国家科技支撑计划项目(2012BAD04B01-06);黑龙江农垦总局攻关项目(HNK125B-04-10)
收稿日期:2015-03-20

