专家模糊控制器在液肥流速控制中的应用
孙 睿,欧阳斌林,孙文峰,李杞超,张继成
(东北农业大学 a.电气与信息学院;b.工程学院,哈尔滨 150030)
专家模糊控制器在液肥流速控制中的应用
孙睿a,欧阳斌林a,孙文峰b,李杞超b,张继成a
(东北农业大学 a.电气与信息学院;b.工程学院,哈尔滨150030)
摘要:为了提高变量施肥的准确性,要求对液体的流速实现过程控制。为此,设计了一个试验台进行针对性的试验,并根据传感器的特点设计了一种专家模糊控制算法。该算法采用目标变量y(t)的变化趋势来制定控制规则,按照模糊控制器的方式划分小区,在其中应用逻辑控制规则,来构建控制算法,并在偏差较小时,采用Δ2e(k)按照减速逼近设定值r的概念来引导积分。在流速控制试验台上,进行阶跃及过程控制试验,将获取的数据画出曲线。通过试验找出各划分小区的比例或积分系数,并证明该方法在稳压阀工作的范围内,可以用于过程控制。
关键词:专家控制;模糊控制;增量控制;液肥
0引言
专家模糊控制多数与PID控制结合,一般采用偏差e和偏差的改变量Δe来改变和确定PID参数[1-3],没有用Δ2e的。再复杂一点的被控对象,模糊控制会与神经网络或专家知识库结合,设计控制策略来解决问题[4-7]。本文将一种专家式模糊控制算法应用于流速控制中。这种系统的难点是流速传感器很少,一般用脉冲输出式的流量传感器。流量传感器能够精确地计量流过的液体的总流量(L),对时间长短没有要求。而控制流速(L/min),对流量和时间都有要求,才能控制好流速。农业中的变量施肥要求控制液体肥的流速才能保证实时施肥量的准确,且流速过程控制的调整时间越短越好。脉冲式流量传感器计量准确,但反映流速相对滞后,需要一定时间和脉冲量才能准确计量流速,如果时间太短,换算出的流速误差大,会影响控制精度和系统稳定性。针对该问题,设计了专家式控制和模糊控制相结合的算法。采用增量式控制,在偏差较小时采用Δ2e引导积分来加快减少静差。结果表明:当偏差小到一定程度后具有一定的稳定性,不容易受扰动而波动,从而达到流速过程控制调整时间短的目的。
1控制实验台设计
试验台的控制系统如图1所示。从流量计F换算出被控变量流速y(L/min),出口外接4个喷嘴,也就是说压力不是直接对大气开口的。为了保证流速的稳定调节,用稳压阀N来保证压力接近于恒定的状态,如在0.15~0.3MPa。这样选择的泵D要足够大保证压力稳定,也就是使稳压阀N处于正常工作的状态,稳压阀有一定的回流存在。当压力稳定时,流速y就可以用调节阀P的开度来调节。
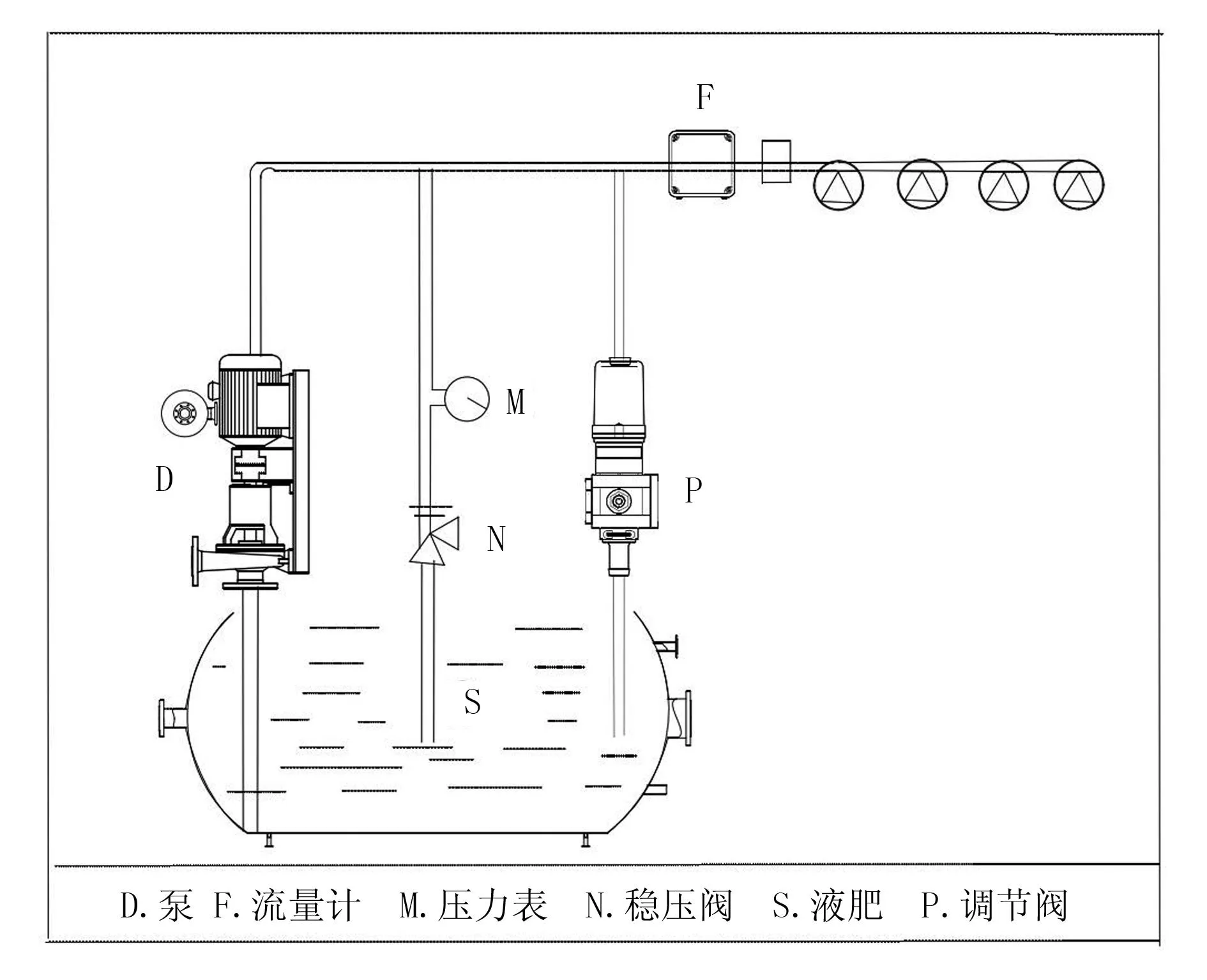
图1 控制系统示意图
当P全闭时,y最大;当P全开时,y=0最小。将P的开度划分为100份,则调节阀从全闭到全开的过程为u=0~100%,输出目标变量y会从最大到接近0。实际上阀的开度与流速y不是线性的,阀在半开时(u=50%)流速y≈0。由于多种因素的影响,如果开环控制流速,流速是不稳定的。也就是一定的开度不一定始终对应一定的流速。而闭环过程控制时,从一个流速变到另一个流速,需要一定的调整时间,调整不好,波动很大,时间就会延长。
2控制原理和算法
不考虑当前u的开度u(k),从e、Δe和Δ2e找出u的增量Δu的输出控制规则,并用这些规则来建立控制规则。当给定值为r,实际测量值为y,则偏差e(k)=r-y(k),Δe(k)=y(k)+y(k-1),Δ2e=-y(k)+2y(k-1)-y(k-2)。由流量计的脉冲来测量流速要进行一次时间变化率计算,在短时间内确定精确的流速偏差和偏差的时间变化率相对更难,所以只能延长时间来提高测量流速的精度。权衡利弊,选择从e、Δe和Δ2e的符号来确定y的变化趋势,从而决定当前输出控制增量Δu(k)。图2中,y在r下方,e>0,下一步的y希望向上发展,u的开度要求减小(关一点),即将要输出的控制增量Δu(k)<0;反之,y在r上方r<0。同时,将要输出控制增量Δu(k)>0(开一点)。


由于设计调节阀的全关u=0,全开u=100,所以添负号。即当e<0增加开阀量,当e>0减小开阀量。增量的程度,用参数K1来决定,K1设计在1~10之间可选择:K1太大时,y会多次超调;K1太小时,会使Δu(k)过早为零而失去调节能力,相当于比例控制。
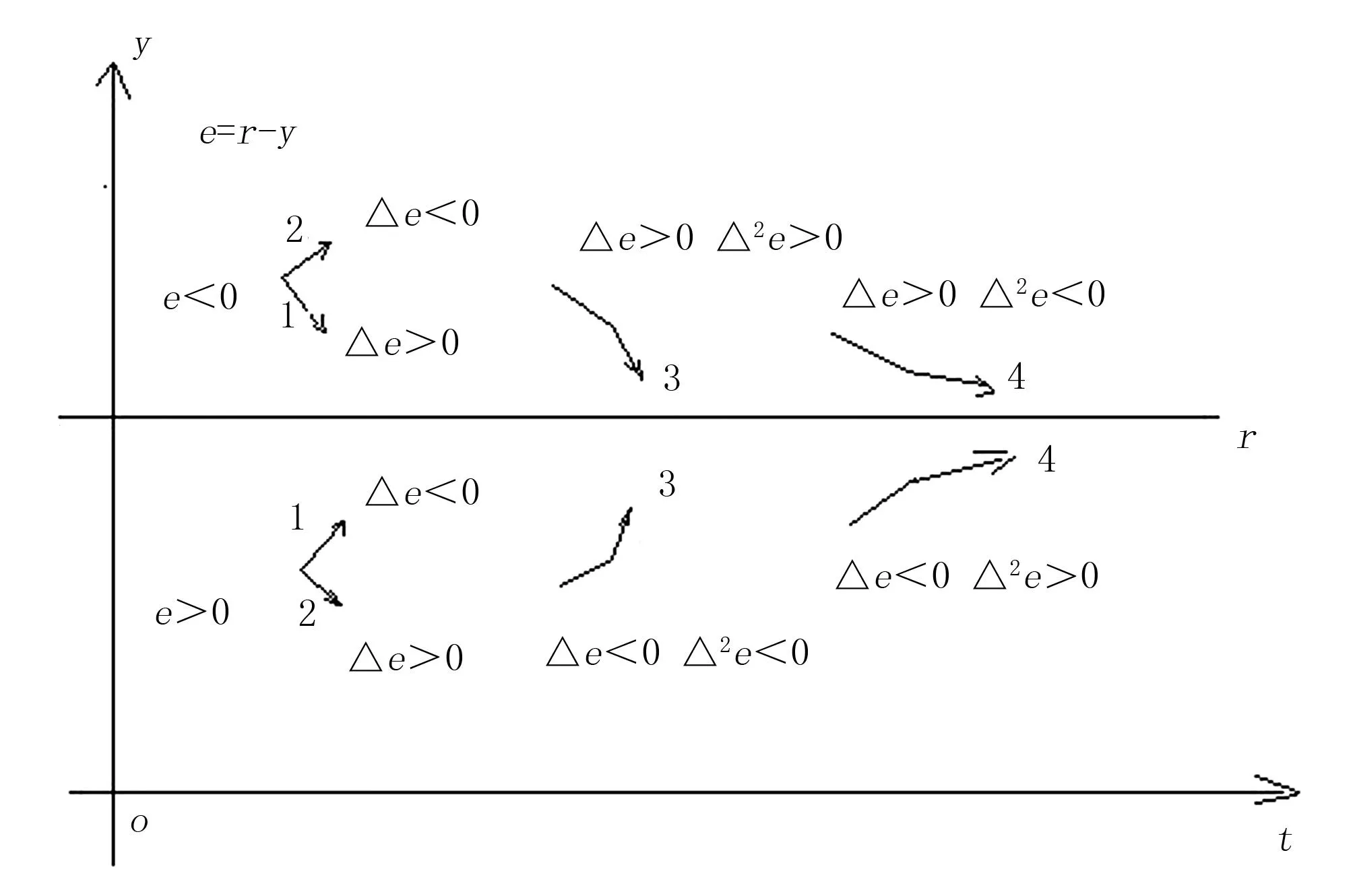
图2 被控变量y的变化趋势

(1)当y朝着r方向逼近时(图2中趋势1),Δu(k)=0,维持原来的u不变,即不调整,有
if[e(k)>0&&Δe(k)<0] Δu(k)=0
if[e(k)<0&&Δe(k)>0] Δu(k)=0
(2)当y背离r变化时(图2中趋势2),则微调输出Δu(k),有
if[e(k)>0&&Δe(k)>0] Δu(k)=-K2e(k)/eM
if[e(k)<0&&Δe(k)<0] Δu(k)=K2e(k)/eM

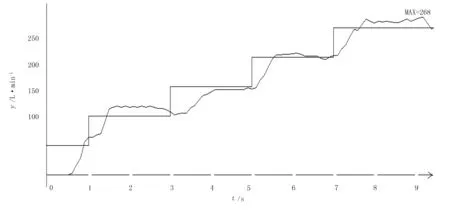
4) 在y被锁定在|e| (1)当y减速接近r时(图2中趋势4),做正常积分,if[e(k)>0&&Δe(k)<0&&Δ2e(k)>0]Δu(k)=-1,略微关一点。if[e(k)<0&&Δe(k)>0&&Δ2e(k)<0]Δu(k)=+1;略微开一点。 (2)当y加速接近r时(图2中趋势3),需要抑制逼近r的速度,if[e(k)>0&&Δe(k)<0&&Δ2e(k)<0]Δu(k)=+2减y的上升速度,略微开两点。if[e(k)<0&&Δe(k)>0&&Δ2e(k)>0]Δu(k)=-2减y的下降速度,略微关两点。 综上所述的控制规则,确定模糊控制输出策略,计算出e(k)、Δe(k)和Δ2e(k),按逻辑条件确定当前的输出控制增量Δu(k)。同时,通过试验找出系数K1和K2的有效范围。执行器是调节阀,调节阀有足够的有效微调开度也是系统控制精度的关键因素之一。通过试验找出调节阀的最小微动步进作为输出的微开量和微关Δu(k)=±1。 3传感器和执行器 传感器采用TeeJet公司的801流量计,输出脉冲,有82个脉冲/L,计量输出的流量,要换算成流速(L/min),需要用单片机定时测量。设输出脉冲为N,则每秒的脉冲增量为ΔN,取前4s的采样值,并考虑减少延迟滞后,采用加权系数,则当前流速为 2ΔN(k-2)+ΔN(k-3)]} 如果选择测量脉冲之间的时间来间接测量流速,比如流速15L/min的脉冲率大约是20个脉冲/s。测量流速y的滞后时间会缩短,但误差大,尤其在计算出e(k)、Δe(k)和Δ2e(k)的误差会更大。在偏差e(k)很小时,进一步影响到它们的符号,从而造成流速y的变化趋势的误判,突然波动,使系统稳定性差,反而延长了调整时间。 调节阀采用TeeJet公司的344BRL,开度从全关到全开需要6s,测试的有效最小微动是1/160s,所以输出控制变量u是用时间秒来衡量的,其增量Δu(k)是调节阀的开关时间,Δu(k)=±1 单位是1/160s,100份最大为1/1.6s。由于系统的性质如图1所示,u的开度位置在0~50%(全关到半开)对y有影响,50%~100%(半开到全开),压力P很小,对y影响很小。所以还设计了压力信号P,检查压力P,使调节阀工作在0~50%的开度范围:压力太小时,将阀关一下;或者开阀时,当压力太小调节阀就不用再开了。 4试验数据分析 设置不同的给定值做阶跃试验,当泵和稳压阀设置固定不变时,从调节阀处于全关状态开始做阶跃试验。由于传感器测量滞后,会出现超调,或者调整时间会很长。设置K1=5、K2=3,分别做r=10、20、25L/min的阶跃试验,试验曲线如图3所示。其中,r=20L/min的曲线形状较好;上端r=25L/min的曲线,阶跃部分不好,是由于系统最大流速小于35L/min,静差还好;下端r=10L/min的曲线表明,调整过大,即设置K1=5对r=10L/min不合适。后面的静差也比较大,是由于图1所示的系统中,更多的液体量回流使u对y的约束能力下降。如果改变稳压阀的设定值,比如减小稳压值P,可以很好地控制r=10L/min;但对于图4所示的r=5~25的过程控制,稳压阀是不能人为再改变的。图4的过程控制曲线表明:该过程控制每20s步进1次,每次步进增量流速为5L/min,调节阀的初始状态为全关。由于系统滞后,第1节超调占用10s,调整时间几乎花了20s。其余的过程没有超调。如果选择适当的初始状态或已知r=5L/min时的调节阀的位置,就可以避免这个巨大的超调。多数调整时间为5s,最大的调整时间是r=15L/min时的10s,控制精度比较好的是r=15、20L/min的两个节点。从该过程曲线看,该控制系统可以用于调整时间小于10s,控制流速在每分钟15~20L/min为最好。而选择这个最佳流速的区间可以通过调整稳压阀来实现。 图3 不同给定值的阶跃试验 5结论 该专家模糊控制采用目标变量y(k)的变化趋势来制定控制规则,按照模糊控制器的方式划分小区,并在其中应用逻辑控制规则,来构建控制算法。在偏差较小时,采用Δ2e(k)按照减速逼近设定值r的概念来引导积分。在流速控制试验台上,通过试验找出各划分小区的比例或积分系数,并证明该方法在稳压阀工作的范围内,其阶跃特性在r=20L/min附近最好,其过程控制特性,在步进5L/min时调整时间小于10s,不超调。在偏差较小时,比较稳定。 图4 过程控制曲线 参考文献: [1]计时鸣,周龙兵,谭大鹏,等.面向软性磨粒流加工的流速模糊控制[J].机电工程,2013,30(2): 160-163. [2]李栋,郝桂明,宋庆军,等.基于模糊控制的火电厂湿法烟气脱硫系统[J].测控技术,2013,32(1): 72-75. [3]孙灿飞,蔡元友,龙海军.电子式氧气调节器中步进电机模糊控制技术研究[J].测控技术,2013,32(4):78-81. [4]王群.基于专家系统模糊PID控制器的研究[J].控制工程,2010,17(5):79-80. [5]崔雅静,杜艳丽,王晓雷.自适应模糊PID控制器的设计[J].控制工程,2008,15(9):128-129. [6]Chiristober Asir Rajan C.Demand side management using expert system[J].Operation of Power Systems,2003(1):440-444. [7]李敏,何平,孟臣.基于模糊神经网络的抽油机节能专家控制器设计[J].计算技术与自动化,2009,28(4): 56-58. [8]梁远博,黄珊珊,雷红玲.基于专家知识的恒压供水控制算法研究[J].工控技术,2009(15): 178-180. [9]杨洋,孟彦京.磨浆机的专家控制[J].微计算机信息,2008,24(9):307-308. [10]关锋,汤伟,冯茜,等.模糊专家控制在制浆中段好氧处理过程中的应用[J].计算机测量与控制,2010,18(5): 1039-1041. Expert Fuzzy Controller in Fertilizer Flow Rate Control Sun Rui1, Ouyang Binlin1, Sun Wenfeng2, Li Qichao2, Zhang Jicheng1 (a.College of Electrical and Information of Northeast Agricultural University; b.College of Engineering of Northeast Agricultural University, Harbin 150030,China) Abstract:In precision agriculture, in order to improve the accuracy of variable rate fertilization, requirements for liquid flow must process control.So designed a test-bed, do corresponding test, according to the characteristics of the sensor design an expert fuzzy control algorithm,which adopts the change tendency of the target variable y (t) to formulate control rules.According to the fuzzy controller way of dividing area.In the areas, application logic control rules,to build the control algorithm.When the error is small, Δ2e be used to guide the integral, according to the deceleration approximation the set value. On the test-bed, do the step test, process control test, and then draw the curve by the acquired data.Through the experiments, the proportional and integral coefficients are identified. And prove that the algorithm is, within the scope of the process control. Key words:expert control; fuzzy; incremental control; liquid fertilizer 文章编号:1003-188X(2016)05-0242-04 中图分类号:S11+6;S224.21 文献标识码:A 作者简介:孙睿(1990-),男,黑龙江大兴安岭人,硕士研究生,(E-mail) 412556546@qq.com。通讯作者:欧阳斌林(1956-),男,湖南宁乡人,教授,硕士生导师,(E-mail) ouyangbl@162.com。 基金项目:黑龙江省应用技术研究与开发技术项目(GC13B307) 收稿日期:2015-04-24