基于粒子群算法的弯道环流式流道多目标优化

马睿佳，魏正英，陈雪丽，马胜利(西安交通大学机械制造系统工程国家重点实验室，西安 710049)

迷宫型灌水器具有结构相对简单、制造方便、成本低，又具有一定的压力补偿性等诸多优点而得到广泛应[1]。迷宫型灌水器主要由3部分组成：进口栅格、迷宫流道和出口。其中迷宫流道利用复杂的壁面边界使其中的水流紊乱，从而引起能量损失，水流在流道内的流动近似表现为紊流，是此类灌水器消能的主要部位，它的结构特性在很大程度上决定着灌水器的2大性能：水力性能和抗堵性能。

传统的求解方法需要对多个目标进行合并,需要选取适当的折中系数,有很强的先验性,增加了决策者决策的难度，如灰靶理论[2]等。为了更好地解决复杂的多目标优化问题，研究人员引进了多目标进化算法，其中，粒子群算法，也称粒子群优化算法(Particle Swarm Optimization 简称PSO)， 是近年来发展起来的一种新的进化算法。PSO 算法是从随机解出发，通过多次迭代寻找最优解也称为非劣解，它也是通过适应度来评价解的品质，它通过追随当前搜索到的最优值来寻找全局最优[3]。本文通过对两大性能的定量分析，在正交实验的基础上，采用粒子群算法对弯道环流式流道进行多目标优化。

1 弯道环流式流道结构设计

1.1 设计依据

弯道环流现象是指在2个连续且相反的90°圆弧连接处，由于前后两端压强的作用刚好相反，会形成2个转向相反的螺旋状前进流，在两个圆弧连接处垂向截面有双环流现象[4]。流体的能量损失包括局部损失和沿程损失，对于灌水器的流道而言，由于内部流道的长度相对较短，能量损失主要为局部损失。利用弯道环流现象可以增加流动内部的碰撞和漩涡，增加流态内部的紊乱程度，从而有效耗能。借鉴上述现象设计弯道环流式流道如图1所示。

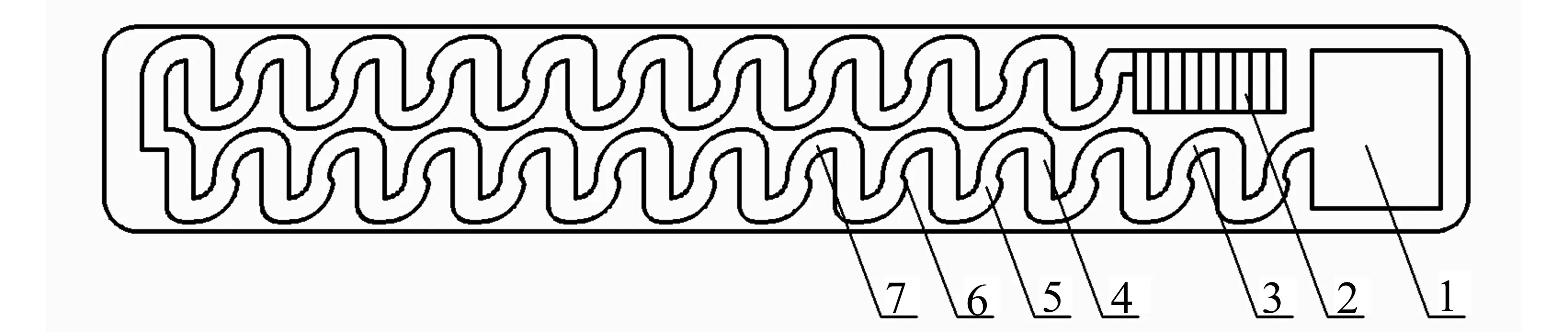
图1 弯道环流式流道Fig.1 Bend circulating current emitter 注：1-出口；2-进口；3-流道；4-直线过渡段；5-宽弯段；6-圆弧渐缩段；7-细弯段。

1.2 流道结构参数化

流道单元包括直线过渡段、宽弯段、圆弧渐缩段及细弯段4部分，如图1所示。宽弯段和细弯段分别为2个同心圆弧构成，且2个部分的圆心位于同一水平上，直线过渡段与2段圆弧外围进行相同大小的圆弧连接，圆弧渐缩段为过渡辅助。流道单元设计为宽进窄出，在圆弧渐缩段产生渐缩、碰撞及本身的螺旋涡旋损失，进入直线过渡段后又产生渐扩损失。如图2所示，提取流道中结构参数，宽弯段的内径为R1，直线过渡段两端的过渡圆弧半径都为R2，细弯段的内径为R3，直线过渡段宽度为H，2段圆弧的外径保持不变，宽弯段外径为1.3 mm，细弯段的外径为1.4 mm，渐缩段为与宽弯段相切的且必须通过A点的圆弧。

图2 流道单元结构Fig.2 Channel unit of emitter

2 流道结构正交实验设计

2.1 正交实验设计

选择流道参数R1、R2、R3、H共4个因素，不考虑个因素之间的交互作用，加入误差项，选用5因素4水平L16(45)正交表，试验因素水平表见表1，正交实验设计见表2。共16组，采用数值模拟的方法，通过建模-网格划分-FLUENT计算的方式对流道性能参数进行提取分析，建立流道结构参数与灌水器2大性能之间的目标函数。

表1 正交实验因素水平 mmTab.1 Factors and levels of orthogonal experiment

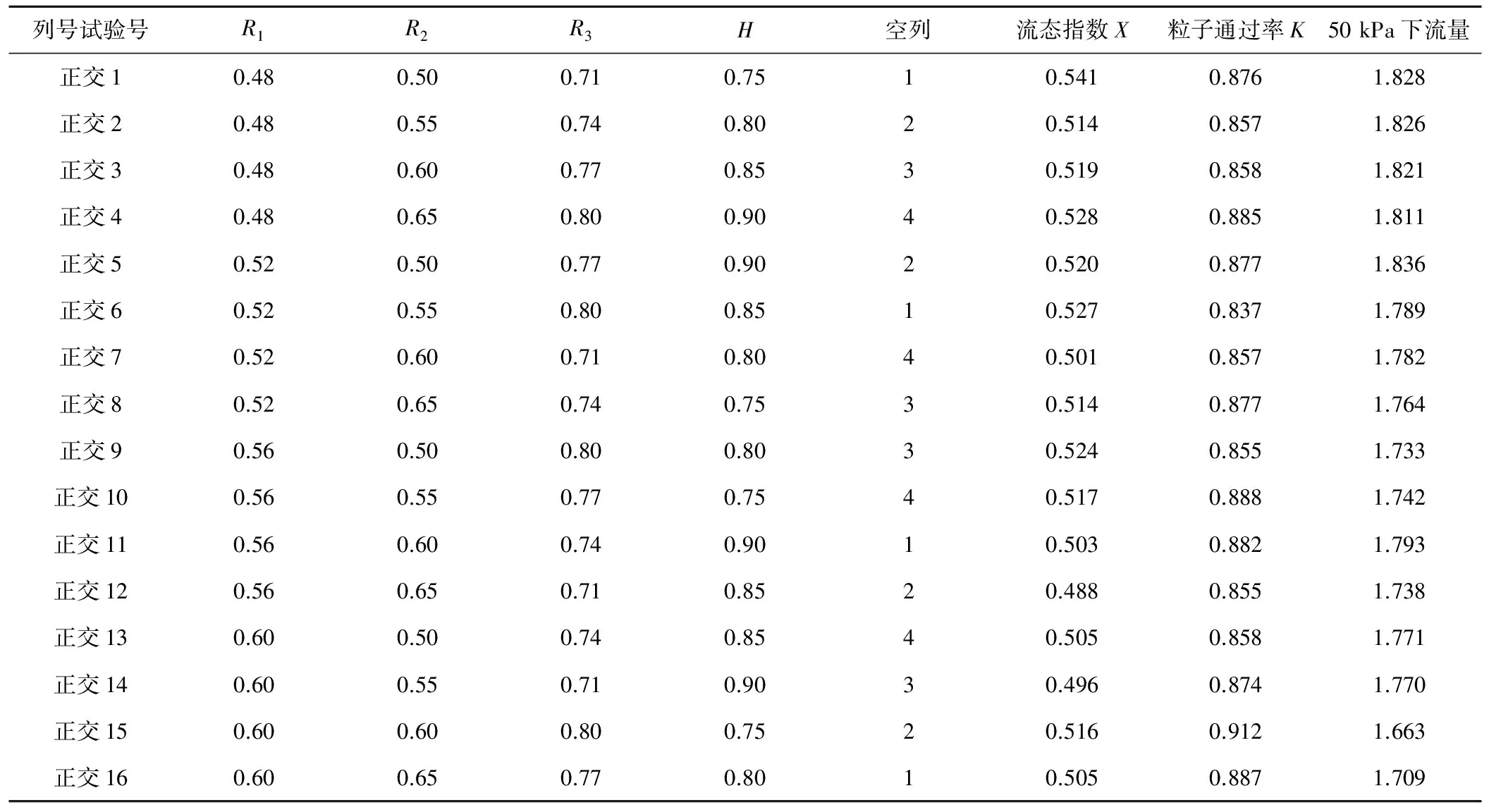
表2 L16(45)设计及试验结果Tab.2 L16(45) design table and experiment results

2.2 数值模型

灌水器流道深度为1 mm,流道进出口采用六面体结构网格划分，流道部分由于多圆弧部分，采用四面体网格划分，网格密度为0.1 mm,总网格数为58万个，细化网格密度分别为0.08和0.06 mm，统计质量流误差不超过1%，但计算耗时分别增长至2～3倍。流道进口为压力进口，出口为大气压。模型采用标准k-ε模型，近壁面选用标准壁面函数，采用SIMPLE算法，二阶离散格式进行离散，收敛精度为10-4。采用离散相模型进行流道内部固液两相流的研究[4]。

2.3 正交实验结果分析

取流态指数作为水力性能的衡量指标，粒子通过率作为抗堵性能的指标，进行16组数值模拟，分别采用直观比较分析、方差分析、线性回归分析等方法对表2进行分析，并得到结构参数与2个指标的回归模型。

(1)流态指数分析。通过直观分析可知各结构对流态参数影响为R1>R3>R2>H，根据流态指数因素-指标图3，选择流态指数的极小值，可知各因素的最佳组合为R1=0.6 mm，R2=0.65 mm，R3=0.71 mm，H=0.85 mm，此组合没有在正交组合中出现。对其进行方差分析，对α=0.1，查表可知F0.1(3,3)=5.39，结果如表3所示，可知R1对结果的影响一般显著，其他参数对结果影响不显著。用SPSS软件对数据进行回归分析，得到流态指数与各结构参数的回归模型为：

X=3.022-1.511R1-0.989R2-2.325R3-2.239H+

1.243R21+0.781R22+1.667R23+1.319H2

(1)

表3 流态指数方差分析结果Tab.3 Variance analysis results of flow index

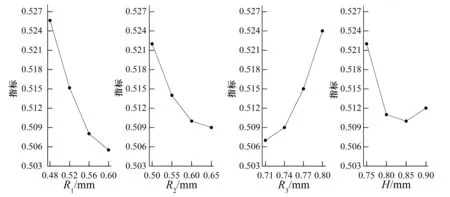
图3 流态指数因素-指标图Fig.3 The factor-index chart of flow index

模型的相关系数R=0.965，R2=0.931，线性关系显著。将通过回归模型计算的流态指数与正交试验的结果进行比较，二者的相对误差在2.6%以内，回归模型精度较高。

(2)粒子通过率分析。同理，通过直观分析可知流道结构参数对对粒子通过率的影响顺序为H>R1>R2>R3。具有最大的粒子通过率的结构组合为：R1=0.6 mm，R2=0.60 mm，R3=0.74 mm，H=0.85 mm。在相关系数R方为0.878的显著水平下，回归分析得到的粒子通过率与流道结构参数的回归模型为:

K=3.909-3.215R1-0.067R2+3.482R3-8.602H+

3.09R21+0.133R22-2.243R23+5.168H2

(2)

3 基于粒子群算法的流道结构优化

3.1 多目标粒子群算法

粒子群算法是一种随机的基于种群的优化策略，通过模拟鸟群觅食的过程建立的一种优化算法。粒子群算法中，每只鸟作为一个粒子，每个粒子有位置和速度两个属性，在飞行过程中根据自身找到的距离食物最近的位置和整个群体找到最近位置去不断改变自身的前进方向，最后整个群体都会趋向同一个地方，即食物的位置。在原有的粒子群算法基础上，Shi[6]等提出了惯性权重粒子群算法，也称标准的粒子群算法，包括了3个部分，粒子自身的惯性部分、自身认知部分和社会部分。该算法的速度更新公式如下：

vid(t+1)=ωvid(t)+c1ri1,t[Xpbid(t)-xid(t)]+

c2ri2,t[Xgbid(t)-xid(t)]

(3)

式中：ω为惯性权重，描述粒子惯性对当前速度的影响；c1、c2为加速系数；ri1,t、ri2,t为0到1之间的随机数。位置更新公式如下：

xid(t+1)=xid(t)+vid(t+1)

(4)

之后，Clerc[7]等提出了一种带有收缩因子的粒子群算法，在保证算法收敛的同时提高算法的收敛速度。本文采用这种算法对速度进行更新，该算法的描述如下：

vid(t+1)=χ{vid(t)+c1ri1,t[Xpbid(t)-xid(t)]+

c2ri2,t[Xgbid(t)-xid(t)]}

计算取c1=c2=2.05，则φ=4.1，χ=0.729。由式(3)和式(5)可知，2种算法从表达形式来说基本一致，式(5)是式(3)的变形。

多目标粒子群算法(multiobjective particle swarm optimization,MOPSO)中以2004年Coello[8]提出基于精英级策略的MOPSO算法最具有里程碑意义，本文采用该算法进行灌水器结构的优化计算。该算法的具体步骤如下。

(1)随机初始化种群，计算各个粒子的适应度值，将其中的非劣解及其位置信息存入外部档案库REP。

(2)确定粒子初始的个体最优Xpbi(0)和全局最优Xgbi(0)。

(3)迭代次数增加，每迭代一次，更新粒子的速度和位置，其中个体最优位置通过比较单个个体经历过的历史最优位置，同时为每一个粒子选取全局最优，全局最优采用自适应网格法和轮盘选择法[9]从外部档案库REP中选取一个。

(4)迭代次数增加，直至满足终止条件。最终外部档案库REP保存的就是所需要的最优解。

外部档案库REP的作用机制包括以下几个方面：首先，每一次迭代得到的全部粒子中的非劣解与上一次迭代得到的REP内的值进行比较，若新的非劣解被REP内原有的任一解支配，则无法进入REP内；若REP内的所有值都无法支配新的非劣解，则新的非劣解进入；若新的非劣解可以支配其中的某个非劣解，则原来的非劣解丢弃，新的非劣解进入REP内。当外部档案库REP达到数量上限时，采取二次准则对里面的元素进行保留，即网格内稀疏位置的元素具有优先保留权。

3.2 基于MOPSO的弯道环流式流道结构优化

灌水器流道多目标优化的目标函数由上文得到如下：

MinX=3.022-1.511R1-0.989R2-2.325R3-

2.239H+1.243R21+0.781R22+1.667R23+1.319H2

MaxK=3.909-3.215R1-0.067R2+3.482R3-

8.602H+3.09R21+0.133R22-2.243R23+5.168H2

其中，结构参数的约束范围为：

(6)

由于优化目标是找到具有优良的水力性能及抗堵塞性能的小流量灌水器，故将流量作为额外的约束标准，流量回归方程由上述正交实验获得：

Q=2.319-0.803R1-0.253R2-0.343R3+0.354H

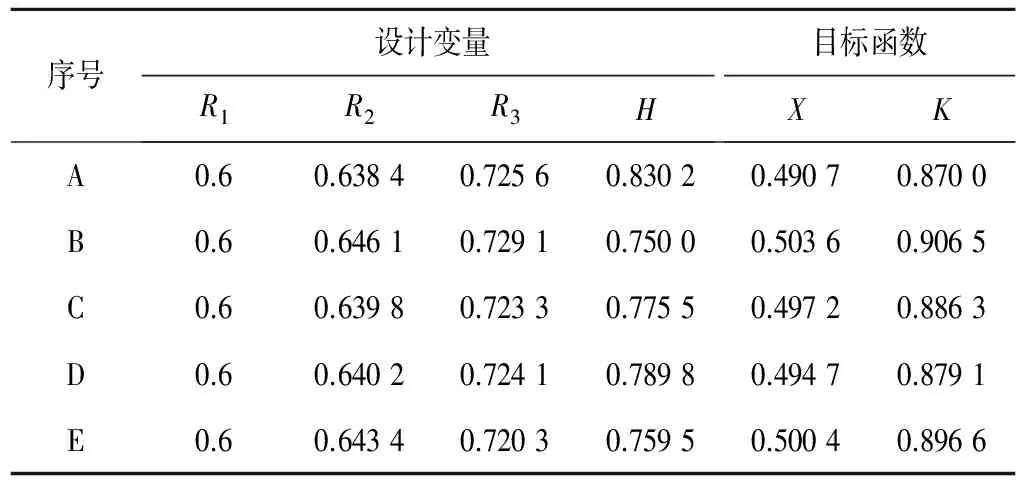
1.5

(7)

其中设置种群规模为100个，迭代次数为100次，分别比较经过初始代、30次、70次、100次迭代后的非劣解集如图4所示，可知粒子通过率K随着流态指数x的增大而增大，基本上保持为线性关系。而理想的结果为粒子通过率越大且流态指数越小越好，故可知两者是相互抵制的，在得到非劣解集后，仍需要人为选择两者关系的权重来确定相应的组合。分别在迭代第100次得到非劣解集中选取5个点，如图5所示，并列出对应的结构参数的组合，如表4所示。

由表4可知，并对其中非劣解集中的点的结构参数及目标函数值分析可知，R1的大小基本为0.6，其他3个参数的可浮动量的大小分别为H最大，R2次之，R3最小。说明R1的取值对2大性能的影响很大，只有在取值为0.6的时候才可以得到最优值，而非劣解集的前沿分布主要由H和R2的大小决定。同时，对比前面的正交实验结果可知，前面的最佳组合基本围绕在参数变量的附近，可知正交分析与多目标粒子群算法的正确性。得到非劣解集后，应当根据设计需求 期、抽穗期、灌浆期的适宜灌溉控制下限标准(占田持%)分别为45%、65%、70%、65%，且在生产中尽量避免出现长期连续干旱现象。

图4 迭代过程中非劣解集的进化过程Fig.4 Evolutionary process of non dominated solution set in the iterative process

图5 取点位置图Fig.5 Location of point

表4 非劣解参数信息Tab.4 Parameters of non dominated solution

□

[1] 路振广，孟春红，王晓丽.基于遗传算法的冬小麦优化灌溉制度研究[J].人民黄河，2009,31(11)：76-78.

[2] 刘 钰，汪 林，倪广恒，等.中国主要作物灌溉需水量空间分布特征[J].农业工程学报，2009,25(12)：6-12.

[3] 高 阳，黄 玲，李新强，等.开花后水分胁迫对冬小麦旗叶光合作用和保护酶活性的影响[J].水土保持学报，2013，27(4)：201-206.

[4] 申孝军，孙景生，刘祖贵，等.灌水控制下限对冬小麦产量和品质的影响[J].农业工程学报，2011，26(12)：58-65.

[5] 徐建文，梅旭荣，居 辉，等.黄淮海地区冬小麦关键生育期不同灌溉水平对产量影响的模拟[J].作物学报，2014，40(8)：1 485-1 492.

[6] 姚 宁，宋利兵，刘 健，等.不同生长阶段水分胁迫对旱区冬小麦生长发育和产量的影响[J].中国农业科学，2015，48(12)：2 379-2 389.

[7] 王俊儒，李生秀.不同生育时期水分有限亏缺对冬小麦产量及其构成因素的影响[J].西北植物学报，2000，20(2)：193-200.

[8] 闫永銮，郝卫平，梅旭荣，等.拔节期水分胁迫-复水对冬小麦干物质积累和水分利用效率的影响[J].中国农业气象，2011，32(2)：190-195.

[9] 霍治国，李世奎，白月明，等.冬小麦中轻度水分胁迫的增产节水效应研究[J].自然资源学报，2003，18(1)：58-66.

[10] 银敏华，李援农，周昌明，等.调亏灌水和分蘖干扰对冬小麦生长的补偿效应[J].应用生态学报，2015，26(10)：3 011-3 019.