不同水位预报方法在黑龙江干流的应用研究

赵思远，郝振纯，刘文斌(.河海大学水文水资源与水利工程科学国家重点实验室，南京 0098；.黑龙江省水文局，哈尔滨 5000)

0 引 言

水位和流量是指示河流汛情的两个最基本水文要素。流量是洪水波运动的本质，水位则是洪水波形状的表现。水位必然与流量有关，但还要受到河道断面几何形状、水面比降、冲淤变化、回水顶托、人工控制的影响，因此，水位预报比流量预报更复杂[1]。

国内在水位预报方面，多年来一直主要沿用古老的相应水位法和流量演算-水位流量关系转换法，又称为经验分析法。采用该法建立的预报模型，用于有回水顶托、冲淤变化和人工控制河道，预报精度不高，一般仅用于预报洪峰水位，不宜用于预报水位过程。自20世纪70年代计算水力学问世以来，国内外提出了一系列基于水力学理论的水位计算模型，但大多只适用于稳定河床。实际应用中需较详细的河道断面和糙率资料，且河床特征常受冲淤影响随时间变化，故预报精度不高。系统理论和方法向洪水预报技术的渗透是从50年代开始的。它经历了一个从个别方法的借用逐步到系统理论引入的过程[1,2]。水文统计方法就是基于系统论的观点和思维方式，针对水位、流量等预报对象，根据流域实际情况和物理成因，寻找主要的相关因子，建立预报对象和主要相关因子之间的相关关系，利用相关因子的实际取值来预测预报对象的取值。这种方法简单实用，但模型参数没有明确的物理意义，属于黑箱模型。采用不同系统计算方法结果差异较大，所以预报精度很大程度上依赖于水文资料及模型的求解。

当影响水位变化的组成条件复杂、资料条件不完善时，采用统计类模型方法进行水位要素的预报具有较好的适用性。此外水位系列在时序上具有相依性、突变性和随机性等复杂非线性特征，而从数学模型来看，任何一个具有高阶微商的非线性的多元函数都可用线性函数逼近，即又归结为线性模型[2]。黑龙江是以雨水补给为主、积雪融水补给为辅的河流，全部径流中雨水补给约占75%～80%，融雪水补给约占15%～20%[3]，干流周围缺乏雨量站和温度观测点，且缺少详细的河道工情信息，针对黑龙江干流的水文特性和资料情况，本文以黑龙江干流中游河段长发屯水位站点为研究对象，选取了5种水文统计方法，通过两种途径进行水位过程预报，一种是上下游水位相关，另一种是考虑预报因子和对象的多阶历史水位来预报站点当前水位。

1 研究方法

本文讨论的水文统计方法主要为回归分析方法，包括多元线性回归、多元门限回归、混合线性回归以及基于混合线性回归方法的逐步回归和门限回归(以下简称混合逐步回归和混合门限回归)。前面两种回归分析方法较为简单，水文预报领域应用较多，后面三种方法是建立在多元回归的基础上，加以拓展延伸。

1.1 多元线性回归

多元线性回归分析建模的步骤一般为：选取预报因子，参数估计，模型检验。实际应用时预报因子一般选用上游入流站点水文要素，参数采用最小二乘法估计，最后通过F检验来判断模型是否线性回归显著。设建立的数学模型为：

(1)

1.2 多元门限回归

对实测水文资料建模的时候，整体呈一条线性往往是不现实的，实际情况中，常常是分成几段。基于此类问题，建立了多元门限回归模型。它的总体思路为：先将研究空间分割为N个子空间，然后在每一个子空间上建立多元回归模型。实际中L常取为2或3。形成的数学模型如下：

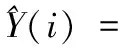
(2)

1.3 混合线性回归

设有mv个变量X1,X2,…,Xmv，其中X1是因变量。X1,X2,…,Xmv的观察值序列为Xij，i=1,2,…,mv，j=1,2,…,nt。定义混合线性回归模型为：

X1t=b0+b11X1,t-p10+…+b1p1X1,t-p10-p1+…+

bmv,1Xmv,t-pmv0-1+…+bmv,pmvXmv,t-pmv0-pmv

(3)

式中，pi0+pi，i=1,2,…,mv为各变量的时间滞后。

式(3)中，因变量X1t不仅可以依赖于其自身历史值X1j，j=t-p10-1,…,t-p10-p1，而且还依赖于自变元的某些历史值Xij，j=t-pi0-1,…,t-pi0-pi，i=2,…,mv。模型的预见期为τ=1+min(p10,p20,…,pmv0)。可以用最小二乘估计法进行模型的参数估计。混合线性回归模型与经典的线性回归模型不同，经典的线性回归模型没有体现出因变量自身前后及因变量与各自变量“过去”的依赖关系；混合线性回归模型又与自回归模型不同，自回归模型没有考虑其他变量对因变量的影响。

实际应用中需要从p=p1+…+pmv个备选变量中挑选出对因变量影响最大的一些因子建立模型。通常采用近似最小信息准则即AIC或BIC准则来挑选回归因子[5,6]。用近似最小信息准则挑选回归因子的思想是：从高阶模型到低阶模型逐步剔除不重要变元，使准则函数为最小的模型便是近似最佳模型。设p阶模型的拟合残差方差为[σ(n)ε]2，则相应的AIC值和BIC值为：

AICn=ln[σ(n)ε]2+2n/p

BICn=ln[σ(n)ε]2+n(lnp)/p

1.4 混合逐步回归

混合逐步回归模型的基本框架及方程形式与混合线性回归模型相似，不同点在于选取自变元时是联合采用AIC准则和逐步回归筛选法来确定模型中应包括的自变元个数及阶数。

逐步回归筛选法是一种双重检验的方法。对于未选入方程的因子，只要它还可以提供显著的解释信息，能使残差平方和下降最多，就可以进入方程；而对于已进入方程的因子，只要在这已建立的过渡方程中不显著，就要从方程中剔除。这是利用求解线性方程中求逆同时并行的方法，使得在计算因子方差贡献和求解回归系数同时进行，计算简便，并且每步都做了检验。通过逐步回归模型引入方程的因子，一定是对预报对象影响显著的因子，此外，它还可以避免因子对预报对象的重复影响。

1.5 混合门限回归

混合门限回归模型就是将门限回归的思想应用到混合线性回归中去，建模的步骤一般为选取预报因子种类，确定门限变量、门限数及门限值，通过AIC准则确定各自变元的阶数，估计各子空间回归系数。此时预报模型为：

(4)

2 应用实例

2.1 长发屯水位过程预报方程

长发屯水位站位于黑龙江干流中游河段与俄罗斯境内结雅河交汇处，其水位因上游河流来水影响，地形复杂，缺少详细的河道工情信息，难以采用水力学模型预报，所以本次采用黑箱模型方法进行长发屯水位过程预报。此外长发屯站距离上游干流黑河水位站较近，预见期较短，而由于本文所采用水文资料时间步长为24 h，因此上游干流入流选用三道卡水位站，支流选用俄罗斯管辖水文站小沙赞卡作为上边界入流站点。图1为长发屯站附近水系概化图。

图1 黑龙江中上游水系概化Fig.1 Water generalization for the upper and middle reaches of the Heilongjiang River

由于该站点位于黑龙江干流中游河段，该区6-9月降水占全年降水量的70%～80%左右，且全年径流量的70%也在这一期间，因此本文中采用的资料数据为三道卡、小沙赞卡(俄罗斯境内站点)、长发屯站2006-2011年的6月1日-9月30日的8∶00水位时间序列，黑河站2006-2011年6月1日-9月30日的8∶00雨量时间序列。

设三道卡、小沙赞卡、长发屯站水位时间序列分别为Z1t,Z2t,Z3t，表示第t日8时水位，m；对各站点水位作相应的一阶差分记为X1t=Z1t-Z1t-1,X2t,X3t同前，称为各站点第t日8时水位涨差，m；P1t代表黑河站分区第t-1日8时至第t日8时雨量，mm。

2.1.1上下游水位相关

通常上游洪水过程与下游洪水过程具有很好的相关性，因此在做下游洪水水位预报时，上游过去洪水水位过程应该是重要的影响因子。以三道卡、小沙赞卡站的洪水水位Z1t-1、Z2t-1为模型输入，预报长发屯站洪水水位Z3t。

长发屯站水位过程多元线性回归模型为：

Z3t=b0+b1Z1t-1+b2Z2t-1

(5)

长发屯站水位过程多元门限回归模型为：

(6)

2.1.2考虑多阶自变元历史值

为了尽可能准确地预报站点水位，消除水位的非平稳性影响，因此对水位时间序列作一阶差分变换(即水位涨差)，同时考虑了区间雨量因素对水位涨差的影响。长发屯站混合回归模型水位过程预报计算步骤为：将该站点上边界入流t日8时以前水位涨差及汇流区间黑河站t-1日8时以前雨量作为模型的输入，计算得该站点t日8时水位涨差预报值，再加上该站点t-1日8时水位，可得该站点t日8时水位预报值。

混合线性回归模型的数学公式为：

X3t=b0+b11X3t-1+b21X1t-1+b22X1t-2+

b31X2t-1+b32X2t-2+b33X2t-3+b41Pat-1

(7)

式中：Pat-1为黑河站第t-1日8时至第t日8时雨量，mm。

混合逐步回归模型的数学公式为：

X3t=b0+b11X3t-1+b21X1t-1+b22X1t-2+

b31X2t-1+b32X2t-2+b41Pat-1

(8)

逐步筛选分析中认为小沙赞卡第t-3日8时水位涨差对预报对象贡献偏小，在显著性水平0.1下，剔除该因子；此外，引进因子的顺序即因子对预报对象的方差贡献从大到小为：X3t-1，X1t-1，X1t-2，X2t-1，X2t-2，Pat-1。

混合门限回归模型的数学公式为：

(9)

在混合门限回归方程中，门限变量Z3t-1是根据预报对象与各预报因子之间的互相关系数取最大选取出来的。而在率定阶段不断对门限变量研究空间进行分割拟合方程，当模型总残差平方和最小时，即确定门限数为2，门限值为8.54。

2.2 预报精度评定

长发屯水位站点采用2006-2010年汛期(6-9月)的水文观测资料率定相应的水位过程预报模型，采用2011年汛期的水位观测资料验证该站的水位过程预报模型，该站点的有效预见期为24 h。根据《SL250-2000水文情报预报规范》，可以采用许可误差和确定性系数作为方案精度评定标准，变幅均方差σΔ和确定性系数DC按下式计算：

(11)

按上述评定准则，取预见期内的变幅均方差作为许可误差，长发屯站通过上下游水位相关进行水位过程预报的两个预报方案中，多元线性回归模型预报合格率在率定期内为62.0%，验证期内为60%以下，不可用于作业预报；多元门限回归模型预报合格率在率定期内为62.5%，验证期内为68.9%，评定为丙等预报方案，可用于参考性预报。这两种多元回归模型预报结果较差，是因为通过简单的上边界站点入流而建立的线性一阶回归方程并不能有效逼近具有非线性变化规律的水位，且模型没有考虑因变元自身历史值。而通过考虑多阶自变元历史值进行水位过程预报的三个混合回归模型预报方案中，率定期和验证期内预报合格率均达到85%以上，确定性系数也都为0.98以上，因此各混合回归模型预报方案均评定为甲等预报方案，可以用于作业预报。长发屯站的验证结果见表1，汛期(6-9月)水位过程洪峰水位预报结果见表2，预报模型的拟合效果见图2-5。

表1 长发屯站2011年汛期水位过程预报精度统计Tab.1 Precision of water-level forcasting of the Changfatun station for flood season of 2011

表2 长发屯站2011年汛期洪峰水位预报结果 mTab.2 Forecasting results of water-level of flood peak of the Changfatun station for flood season of 2011

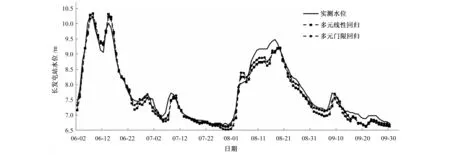
图2 长发屯站多元回归模型2011年汛期(6-9月)水位过程预报检验Fig.2 Verifying the validity of water-level forecasting for flood season of 2011(June to September) by using multiple regression models

图3 长发屯站混合线性回归模型2011年汛期(6-9月)水位过程预报检验Fig.3 Verifying the validity of water-level forecasting for flood season of 2011(June to September) by using multivariate hybrid linear regression method

图4 长发屯站混合逐步回归模型2011年汛期(6-9月)水位过程预报检验Fig.4 Verifying the validity of water-level forecasting for flood season of 2011(June to September) by using multivariate hybrid stepwise regression method

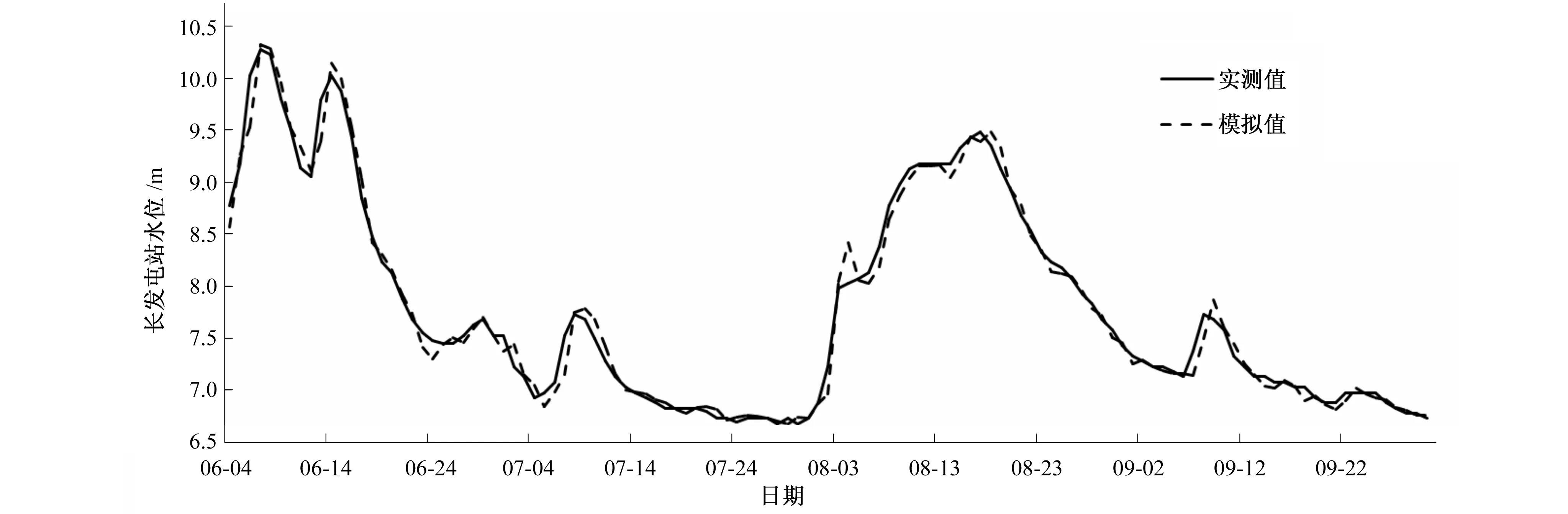
图5 长发屯站混合门限回归模型2011年汛期(6-9月)水位过程预报检验Fig.5 Verifying the validity of water-level forecasting for flood season of 2011(June to September) by using multivariate hybrid threshold regression method

由表1可以看出，根据上下游水位相关预报，多元门限回归比多元线性回归模型的结果好；而考虑多阶自变元历史值预报，3个模型的预报效果相差不大，其中混合门限回归当属最优，该模型的各项预报指标均优于其他模型。

由表2可以看出，预报非线性的水位过程洪峰，3种混合回归模型明显优于通过上下游水位相关的两种模型，其中混合门限回归模型预报洪峰水位与实测洪峰水位误差最小，最为稳定。

除了长发屯站点以外，本文还将5种水位过程预报方法应用于黑龙江其他水位站点上，其中3种混合回归模型均表现良好，在预报精度上均能达到甲等；当上边界入流仅有一个水位站点时，另外两种多元回归模型在预报精度上也能普遍能达到乙等以上。在本实例研究中还需要说明的是，混合逐步回归模型较于混合线性回归模型筛选剔除了一个预报因子(小沙赞卡第t-3日8时水位涨差)，且最后预报精度能够不差于混合线性回归模型，但用逐步回归方法挑选回归因子，使用F检验方法进行检验时，如果置信水平选取不当，可能导致误判，使得预报精度变差，这种情况应当尽量避免；此外，相对于混合线性回归模型，虽然混合门限回归模型预报效果较之都要高一点，但是该模型结构较为复杂，在混合线性回归模型程序基础之上又多了自变元与因变元互相关系数计算模块、门限元分段模块、F检验计算模块，且在率定过程中需要对门段数进行试算，不如混合线性回归模型方便，稳定，在对预报精度要求不高的情况下，简单的方法要优于复杂的。

3 结 论

针对黑龙江干流汛期洪水的特点和防洪减灾决策的需求，本文采用多元回归模型和基于混合线性回归模型的各种统计相关方法，建立了黑龙江干流中游长发屯站点的水位预报模型，模型有效预见期为24 h。率定和验证结果表明，通过简单的多元回归关系来建立上下游水位相关关系，预报效果并不理想，而其他三种混合回归模型预报方案的预报精度均能达到甲等。因此，所提出的混合回归模型方法具有一定的精度和较好的适用性，可以用于作业预报。

上述研究表明，对于水位过程预报，简单的水文统计方法是行之有效的，且模拟精度较高，适用于那些受上游干流及众多支流来水影响，地形复杂，缺少详细的河道工情信息的河流站点作水位预报。应当指出的是，由于大部分的水文统计方法是输入、输出的黑箱模型，其结构和参数全由水文资料率定，倘若流域或河道情况发生变化，对今后每年开展的预报工作，增加新的水文资料的同时，需采用延长后的资料进行实时率定和验证，优化模型参数，提高预报方案精度。

□

[1] 黄国如,朱庆平,马 骏,等.水位演算模型及其在水位预报中的应用[J].水文,1999,(2):1-6.

[2] 葛守西.现代洪水预报技术[M].北京:中国水利水电出版社,1999:1-23.

[3] 牟金玲,狄 娟.黑龙江干流中上游段水文特性[J].黑龙江水利科技,2007,35(2):101-102.

[4] 李致家,孔祥光.非线性水文系统的实时预报方法比较研究[J].水文,1997,(1):24-28.

[5] 张显扬,董增川,王建群,等.雅鲁藏布江尼洋河流域洪水预报方法研究[J].河海大学学报(自然科学版), 2005,33(5):530-533.

[6] 胡 炜,董增川.统计相关分析在太湖流域水位预报中的应用[J].水利经济,2008,26(3):55-58.

[7] Phien H N, Kha N D A. Flood forecasting for the upper reach of the Red River Basin, North Vietnam[J]. Water S A,2003,29(3):267-272.

[8] SL250-2000，水文情报预报规范[S].