利用数字流域特征提高滞后演算法的空间移用效果研究

李 丽，徐秀丽，王加虎，袁 莹，习雪飞

(河海大学水文水资源学院，南京 210098)

无历史实测径流资料地区(简称无资料地区)的水文预报，是水文水资源研究的热点和难点[1]，主要是因为常用的水文模型大都需要利用历史实测径流资料率定相关参数。很多学者从两个方面进行无资料地区的水文预报研究，主要包括两个方向：一是建立具有物理机制的水文模型、不依赖实测历史资料确定模型的相关参数[2]；二是从现有的模型出发，研究模型参数的空间规律性，将有资料地区的水文模型参数应用到无资料地区[3]。

在生产实践中，以中国洪水预报系统为代表，大量使用着以经验模型或概念性模型为基础的预报方案[4]，这些方案在长期的应用过程中不断被检验和校正，是十分宝贵的财富。如何在无资料地区的水文预报过程中充分利用这些已有成果，是一个很有挑战的问题。本文以概念性汇流模型中常用的滞后演算法为例，利用数字流域特征对汇流参数进行换算后，区间移用的效果较好，对于其他概念性模型的参数移用具有借鉴意义。

1 产流计算

为了减少产流模型参数移用对结果的影响，本文选用SCS模型计算产流。SCS模型结构简单，产流参数较少，又能够客观反映土地利用情况、土壤类型及前期土壤含水量对降雨径流的影响，适用于无资料地区产流计算[5]。

SCS模型最初是由美国土壤保持局于1954年针对小流域洪水设计而开发的，后来又演变出许多不同的形式。SCS模型的产流计算公式为：

(1)

式中：R是产流深，mm；P是降雨总量，mm；S是最大潜在降水损失，即降水与径流之间可能的最大差值，mm；Ia为降水的初期损失，mm。

Ia是高度变化的，表现为前期条件对降水初始损失的影响，包括地面洼地蓄水、植物截留、下渗和蒸发等。模型制作者根据美国农业集水区的资料经验公式将其近似确定为：

Ia=0.2S

(2)

S通过径流曲线数CN与土壤和流域覆被条件建立关系，计算公式为：

(3)

径流曲线数CN是一个无量纲参数，是模型中唯一的产流参数，反映了不同条件对产流的影响。根据土壤质地将土壤分为A、B、C、D 4种类型。根据前5 d的降水总量可将土壤湿润程度划分为干旱(AMCⅠ)、平均(AMCⅡ)、湿润(AMCⅢ)3种状态，且不同湿润状况的CN值有相互转换关系。确定其值需要土壤类型、土地利用方式及前期径流条件3组数据，不同的组合对应不同CN[6]。

经典的SCS模型无法计算出逐时段洪水过程，本文按照李丽等[7]的研究成果，建立了两水源改进SCS产流模型，主要包括：用递推方法计算出逐时段产流量；用流域土壤的平均饱和水力传导度进行分水源，将产流划分为快速径流和慢速径流两部分。

2 汇流计算

2.1 基本原理

常用的概念性汇流计算方法包括单位线法、马斯京根法和线性水库法(滞后演算法), SCS原始模型中采用无因次单位线法计算径流输出过程，其单位线根据经验公式确定。而本文着重研究滞后演算法，滞后演算法是一种传统的概念性汇流方法，且在各水文模型中应用较为广泛，故舍弃原有汇流结构。本文尝试采用基于数字流域特征的参数移用新方法，探讨滞后演算法的参数外延能力。

一个单元流域某种水源的水量平衡方程为：

(4)

式中：I、Q分别为单元流域该种水源的入流、出流量，m3/s；W为单元流域内的蓄量，m3。

假定该水源的槽蓄方程是线性的：

W=kQ

(5)

就上面两式进行差分求解，时段长为Δt,在i-1,i两个时刻进行差分，假定k是常数，并引入滞时T通过推导有：

(7)

式中：k为线性的蓄泄系数，h；Cs为线性水库的消退系数，考虑单元流域的调蓄坦化作用；1-Cs为线性水库的出流系数。

线性水库法(滞后演算法)汇流参数移用的时候，滞时和出流系数设计参照如下的方式由参证站换算到目标站。

2.2 滞时移用

水流在流域坡面运动的快慢程度在滞后演算法中用滞时表示，滞时与数字流域的平均坡度S成反比、与流域的平均出流路径长L成正比[8]，即：

(8)

式中：t是名义滞时。

在区间移用时:

(9)

式中：T是模型适用的汇流滞时，滞时的最小值是0，h。

2.3 出流系数移用

出流系数反映了流域对自由水除流速之外的约束程度，面积越小的流域，出流系数越接近1；面积越大的流域，该系数越接近于0。在目前的资料条件下，简单按照线性关系拟定了如下移用换算公式：

(10)

式中：A是流域面积，km2；K是线性水库出流系数即1-Cs。

假定参证站面积为1 000 km2，率定的出流系数是0.8；目标站的面积是500 km2，目标站的出流系数为[1-(1-0.8)×500/1 000]=0.9。

3 参数移用效果验证

3.1 目标站的选择

为了检验上述汇流参数移用方法的适用性，选择了资料条件较好的龙里站作为目标站。龙里水文站集水面积221 km2。地处贵州省龙里县龙山镇饶钵山，坐标为东经106°57′，北纬26°28′，龙里站流域多年平均降水量地区变化在1 060～1 250 mm之间，流域平均降雨量为1 105.8 mm。

3.2 参证站的确定

按照李正最等[9]介绍的相似特征指标的灰色关联度分析方法，逐一分析龙里站附近11个有长系列实测水文资料的站点，相似特征指标选定11个有资料站点的流域面积、主河道长、流域平均坡度、主河道长度、形状系数、多年平均降雨量、土壤质地以及林地、草地覆盖面积比例，然后进行关联度计算，选择关联度最大的流域作为参证流域。流域相似性分析的灰色关联度法，已有较为完善的理论研究，避免了人为选择设计参证流域的主观性和盲目性，又使选出的参证站点具有代表性和可靠性，具体确定过程，本文不再赘述。

最后选定修文站作为率定参数的参证站。修文河发源于修文县东北金桥乡，为猫跳河右岸的一级支流，河长32 km，集水面积 228 km2，流向南西，经林家寨、蚌壳堰、石安、马家桥、修文县城至修文河水电站汇入猫跳河。流域地貌大致以县城为界：县城以上24 km 河段为浅丘陵、平坝地貌，村寨、耕地集中；县城以下至河口 8 km河段为山地、峡谷地貌，人口、耕地稀少。

3.3 流域特征提取

本文采用Channel Network Tool-I(简称CNT-I)软件包提取流域特征，CNT-I是河海大学郝振纯教授等开发的提取流域地表水文特征的专用软件包，在复合信息(复合了自然水系位置的DEM)的控制下按照D8法来提取出与自然水系相匹配的流域特征信息，在平原区和洼地的处理上有了很大改善。该软件主要包括栅格河道矢量化、数字水系生成、流域特征提取等功能[10]。

资料来源为贵州省二十五万分之一的天然水系图和美国地球物理数据中心1999年发布的全球陆地1 km基础高程(Global land one-kilometer base elevation, GLOBE)数据，GLOBE数据按照经纬网描述高程的空间分布，其空间分辨率为30″(准1 km)。实际使用时，每个栅格的面积和边长都根据栅格中心点的纬度做了简单校正。提取出的栅格河网如图1所示。

图1 目标站和参证站数字水系Fig.1 Raster river network of target area and reference station

3.4 建模及其他资料

降雨资料取自水文年鉴。选用修文站、金桥、马家桥、程关4站雨量资料，流域面平均雨量计算采用泰森多边形法。蒸发资料采用多年月平均值。植被数据采用中国国家自然地图集中的中国植被区划图。土壤资料采用美国国家航空和宇宙航行局(NASA)哥士德航天中心(GSFC)土地资料同化系统(GLDAS)的5′网格尺度(约10 km)的资料，分类标准为《中国土壤》(科学出版社，1978年，中科院南京土壤所编)中的分类。模型程序用C#开发，计算时段长1 h，预热期30 d。

3.5 验证方法

(1)产流参数的确定：根据修文站与龙里站流域多年平均降雨情况，确定前期土壤湿润程度为平均情况(AMCⅡ)。根据遥感资料，确定修文站与龙里站控制的小流域土壤类型为砂质黏壤土，属于水文土壤分组属C类。不同土地利用类型，前期湿度中等条件下CN值见表1。

表1 不同土地利用方式的CN值Tab.1 CN values of different land-using

加权平均得修文站控制的小流域平均CN值为74.3，龙里站控制的小流域平均CN值为73.5。

(2)汇流参数率定方法：产流参数确定后，通过模型率定出一组汇流参数。模型中采用SCE-UA算法率定模型参数[11]，避免人为调参对结果的影响。SCE-UA算法的基本思路是将基于确定性的复合形搜索技术和自然界的生物竞争进化原理相结合。算法的关键部分为竞争的复合形进化算法(CCE)，是一种可以有效解决非线性约束最优化问题的方法。

(3)参证站汇流参数：在参证站选择10场次洪，率定出的主要参数如表2所示。结果中：洪峰流量按照20%许可误差衡量，合格率为80%；洪水总量按照20%许可误差衡量，合格率为90%；峰现时刻误差绝对值(因为峰现时刻有正有负)的平均值为0.9 h；确定性系数的平均值为0.81。

(4)目标站汇流参数：按照第2节描述的方法，由参证站换算出目标站的汇流参数，如表3所示。

表2 参数率定结果Tab.2 The situation of parameter calibration

表3 参数转换结果Tab.3 The situation of parameter conversion

(5)目标站的验证结果：在目标站选择10场次洪，利用确定好的产流参数和移用换算出的汇流参数，根据目标站的实测降雨资料模拟出目标站的洪水过程，并与实测值相比较。洪峰流量按照20%许可误差衡量，合格率为60%；洪水总量按照20%许可误差衡量，合格率为50%；峰现时刻误差绝对值的平均值为1.5 h；确定性系数的平均值为0.72(见表4)。

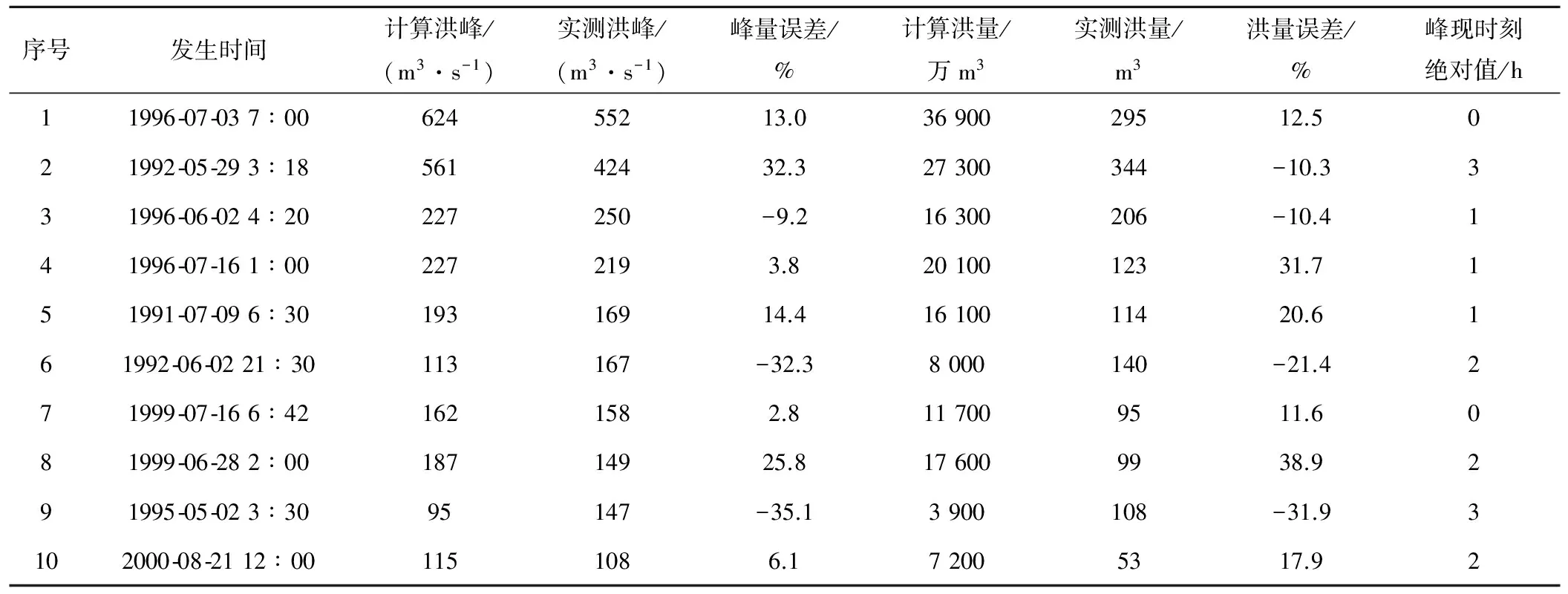
表4 参数移用后的验证结果Tab.4 The results of the improved model with transformed parameter

4 对照试验

同样用上述模型，确定参证站和目标站的产流参数和参证站的汇流参数后，直接将汇流参数应用到目标站，模拟出10场次洪。模拟结果中：峰量拟合的合格率为20%(改进方案为60%)；洪水总量拟合的合格率为40%(改进方案为50%)；峰现时刻误差绝对值的平均值为3.1 h(改进方案为1.5 h)；确定性系数的平均值小于0.10(改进方案为0.72)。

对照试验表明：相对于传统参数直接移用的方法而言，基于流域特征的参数移用新方法拟合效果有了很大改善，在峰量误差、峰现时刻误差以及确定性系数的提高上表现最为明显。

5 结 语

相关研究和本文的对照试验都表明：滞后演算法作为概念性汇流模型的代表，跨区间参数移用后的模拟效果较差。本文利用数字流域特征对汇流参数做换算，得到了较好的跨区间移用效果，相对于直接移用的方法模拟精度得到了明显的改善。研究成果对于应用比较广泛的其他概念性产汇流模型来说，具有借鉴意义。

但同时也发现，单纯的汇流参数转换后移用的模拟效果，和实际作业预报的需求之间仍有一定差距。原因是实际流域产汇流由于流域之间植被、土壤、降雨等的空间差异，产流过程也有所不同，后续研究将针对产流参数的空间差异展开，以期进一步提高参数移用的模拟效果。

□

[1] 谈 戈, 夏 军, 李 新. 无资料地区水文预报研究的方法与出路[J]. 冰川冻土, 2004,26(2):192-196.

[2] 胡彩虹, 郭生练, 熊立华，等. TOPMODEL模型在无DEM资料地区的应用[J]. 人民黄河, 2005,27(6):23-25.

[3] 施 征, 包为民, 瞿思敏. 基于相似性的无资料地区模型参数确定[J]. 水文,2015,35(2):33-38.

[4] 章四龙. 中国洪水预报系统设计建设研究[J]. 水文,2002,22(1):33-35.

[5] 甘衍军, 李 兰, 杨梦斐. SCS模型在无资料地区产流计算中的应用[J]. 人民黄河, 2010,32(5):30-31.

[6] 孙立堂, 曹升乐, 陈继光,等. 改进的SCS模型产流参数在小清河流域的率定[J]. 人民黄河, 2008,30(5):33-35.

[7] 李 丽,王加虎，郝振纯,等.SCS模型在黄河中游次洪模拟中的分布式应用[J].河海大学学报(自然科学版),2012,40(1):105-108.

[8] LI Li, WANG Jiahu, HAO Zhenchun, et al. Appropriate contributing area threshold of a digital river network extracted from DEM for hydrological simulation[C]∥ Hydrological Research in China: Process Studies, Modelling Approaches and Applications. IAHS Publ, 2008.

[9] 李正最. 参证流域灰色相似选择[J]. 四川水利, 1995,16(2):35-39.

[10] 郝振纯, 王加虎, 李 丽,等. Channel Network Tool-的原理与功能[J]. 水文, 2005,25(2):15-19.

[11] 唐运忆, 栾成梅. SCE-UA算法在新安江模型及TOPMODEL参数优化应用中的研究[J]. 水文, 2007,27(6):33-35.