塔河油田氮气与水混注时井筒压力分布计算

胡晓华　吴 锋　李溢龙　杨 强　姚卓成

(1. 西南石油大学油气藏地质及开发工程国家重点实验室， 成都 610500；

2. 川庆钻探工程有限公司长庆钻井总公司， 西安 710018)



塔河油田氮气与水混注时井筒压力分布计算

胡晓华1吴 锋1李溢龙1杨 强1姚卓成2

(1. 西南石油大学油气藏地质及开发工程国家重点实验室， 成都 610500；

2. 川庆钻探工程有限公司长庆钻井总公司， 西安 710018)

摘要：对于气水混合注入井井筒压力的计算，通常是将两相流经修正后近似为单相流处理。将气、水两相分开处理，考虑两相界面效应，建立不同气水比注入条件下的井筒压力计算模型，并根据储层压力对井底流压的影响给出模型的边界条件，最后编程求解井筒压力分布。实例验证计算压力与实测压力的相对误差小于3.56%，平均相对误差为1.71%，均在合理误差范围内。

关键词：塔河油田； 气液混注； 井筒压力； 两相界面

近年来，注氮气提高采收率技术被广泛地应用于塔河油田[1-4]，但是对氮水混合注入过程中，井筒压力分布情况的研究却相对较少。通常的处理方法是将两相流经修正后近似看作单相流[5-6]，采用稳定流动的压降梯度方程对其压力分布情况进行研究[7-11]。这种方法忽略了气水两相间的相互作用，仅适用于气水比很大的情况，其实际应用具有较大的局限性。本次研究基于拉格朗日流场运动法建立井筒气液两相流流动模型，充分考虑了气液界面间的相互作用，适用于任意气、水比的计算。

1数学模型推导

1.1一般守恒方程

对于流场中某固定微元体中某物理量的变化，等于通过微元体表面流入流出的物理量与微元体中源自身产生的物理量之和，即：

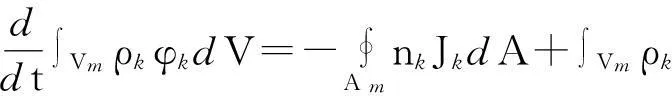
(1)

式中：ρk—— 流体密度；

Jk—— 针对流场特性的流出率；

φk—— 微元体体积源；

φk—— 微元体特性参数；

Vm—— 微元体体积；

Am—— 微元体表面积；

k —— 某相流体，分别为液相和气相。

根据输运公式和格林公式，式(1)可简化为：

(2)

在流场中除去k相本身外，还存在相间界面区。为描述整个流场特性，必须建立界面特性基本方程[11]。

界面区如图1所示，a1、a2为界面区内两相的界面；n1、n2为a1、a2的单位向量(法向量)；界面总厚度和为δ=δ1+δ2，通常δ1=δ2；N为封闭端面的单位向量；∑i为封闭端面；ζi为∑i与ai的交线。界面控制体即为∑i与ai所包围的体积Vi；如果认为δ很小，则n1=-n2，对控制体Vi的积分特性为：

(3)

式(3)即为界面基本方程。式中，φi为控制体内流场特性参数，φi为控制体内流场体积源，ρi为控制体内流体密度，Jk为针对流场特性的流出率，uk为相速度向量。

图1　两相流界面微元图

1.2连续方程

对于一个确定的系统，根据质量守恒定律，有：

φk=1, φk=0, Jk=0

(4)

将式(4)分别代入式(2)、(3)，推导出相内和界面连续方程：

(5)

(ug-ui)ρg=(ul-ui)ρl

(6)

式中：ug—— 气相速度，ms；

ul—— 液相速度，ms；

ui—— 界面控制体速度，ms。

将式(5)分别写成气相和液相的相内连续方程，结合式(6)的界面连续方程，经过连续化，推导出两相连续方程：

(7)

式中：ρm—— 混合物密度，kgm3；

um—— 混合物速度，ms。

1.3动量方程

根据动量定理，引入pk表示相压力，Tk表示剪切应力，gk表示体积力，有：

φk=υk, φk=pk-Tk, Jk=gk

(8)

将式(8)分别代入式(2)、(3)，推导出相内和界面动量方程：

(9)

(ug-ui)ρgug+pg-τg=(ul-ui)ρlul-pl+τl

(10)

将式(9)分别写成气相和液相的相内动量方程，结合式(10)界面动量方程，经过连续化，推导出两相动量方程：

(11)

式中：ur—— 气液两相速度差，ms；

A —— 管道截面积，m2。

1.4能量方程

根据能量守恒定律，有：

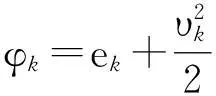
φk=qk+(pk-Tk)·υk

Jk=gk·υk

(12)

将式(12)分别代入式(2)、(3)，推导出相内和界面能量方程：

-▽·qk+▽·[(-pk+Tk)·υk]+ρkgk·υk

(13)

(14)

将式(13)分别写成气相和液相的相内能量方程，结合式(14)界面能量方程，经过连续化，推导出两相能量方程：

(15)

式中：qw—— 热流密度，Wm2。

1.5边界条件

在缝洞型油藏中，井通常设计在溶洞或裂缝上，储层压力的变化对井底流压的作用非常明显。随着注入速度的增加，一方面井筒压力受井口注入压力和注入速度的影响；另一方面储层压力升高，井底流出速度发生改变，使得井筒积液量不断增加，进而影响井筒压力。因此，根据井筒 — 井底 — 储层的相互作用，建立边界条件：

(16)

式中：pr—— 储层初始压力，MPa；

Q —— 注入速度，m3d；

t —— 注入时间，d。

2模型建立

经上述推导，可建立数学模型：

(17)

3井筒压降计算

多相管流中影响每相流体流动的物理参数、混合物密度以及流速都随压力和温度而变，且沿程压力梯度不为常数，因此，多相管流需分段计算，并要预先求得相应管段的流体性质参数。这里采用迭代法进行求解。

迭代法的基本步骤如下：

(1)将任一点(井口或井底)H0作为起点，任选一个合适的迭代步长ΔH作为计算的深度间隔。

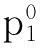
(5)计算该段下端的压力p1。

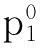
(7)计算下一段压力，重复步骤(2) — (6)，直到计算至井底。

4实例应用

TH油田某井注气过程中进行了3次流压流温测试，始终保持3 989 m3h的速度注入氮气，地层水分别以7.80，8.60，9.75 m3h的速度注入。采用自编程序计算3次测试期间井筒压力分布，并与实测结果进行比较分析(图2)。

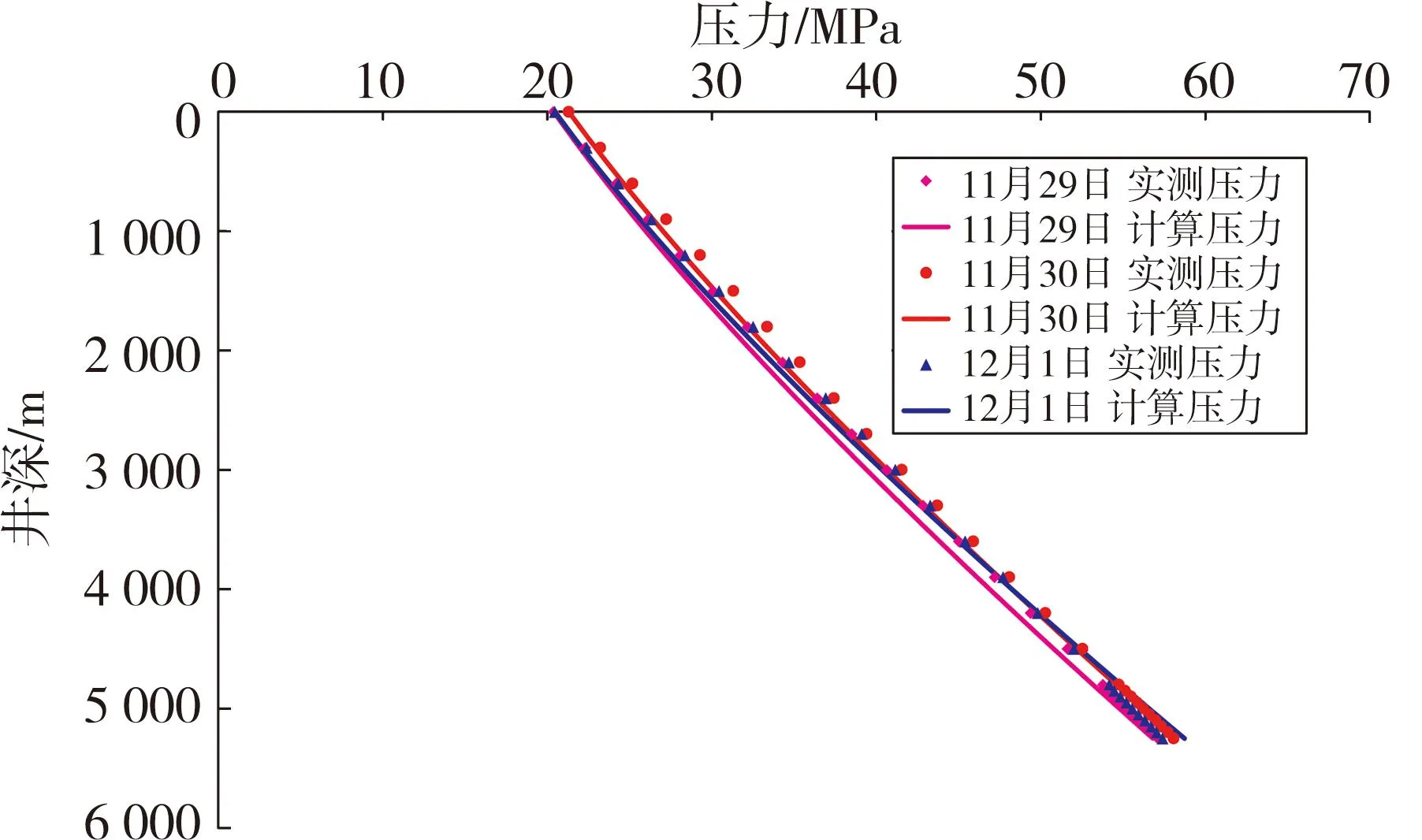
图2　该井实测压力与计算压力对比

如图2所示，该井的井筒不同时刻的计算压力与实测压力相近，两者的相对误差在0~3.56%，平均相对误差为1.71%，误差在合理范围之内。该结果表明井筒压力计算模型准确可靠，可用于氮气和水混注的气井井筒压力分布计算。

5结语

(1)基于拉格朗日流场法和守恒方程建立的井筒压力计算模型，考虑了气水两相界面的影响，适用于不同的气水比注入条件。

(2)针对缝洞型储层给出的边界条件，考虑了储层压力对井底流压的作用，以及井筒压力随注入量的变化。

(3)模型计算与油田井筒实测压力对比结果表明该模型可靠，计算误差在合理范围之内。

参考文献

[1] 王瑞,王倩,魏芳.注氮气在塔河油田凝析气藏的应用及效果[C]重庆市科学技术协会.第三届全国特殊气藏开发技术研讨会优秀论文集.2014.

[2] MUNGAN N. Enhanced Oil Recovery with High Pressure Nitrogen Injection[C]SPEAAPG Western Regional Meeting. 2000.

[3] WUENSCHE R. Nitrogen Jnjection for Enhanced Oil Recovery[C]Annual Technical Meeting. Petroleum Society of Canada. 1978.

[4] CLANCY J P, GILCHRIST R E. Nitrogen Injection Applications Emerge in the Rockies[C]SPE Rocky Mountain Regional Meeting. 1983.

[5] 徐晔,马木提江,李英俊.氮气泡沫在井筒中的压力分布研究[J].油气田地面工程,2004(5):10.

[6] 张奇斌,刘春妍,周淑华.含水气井油管流压梯度计算[J].天然气工业,2007,27(3):83-85.

[7] 杨军,张烈辉,刘娅.CO2气井井底压力计算[J].特种油气藏,2008(1):56-58.

[8] 田卓,苟宏刚,张建华,等.高含水气井井筒压力计算新方法探讨[J].天然气勘探与开发,2007(1):58-59.

[9] 杨志伦.含水气井井筒压力计算方法[J].油气井测试,2007,16(4):4-5.

[10] 陈林,孙雷,苏静,等.注CO2井井筒温度压力分布主控因素分析[J].西安石油大学学报(自然科学版),2014(1):46-48.

[11] 鲁钟琪.两相流与沸腾传热[M].北京:清华大学出版社,2002：44-49.

The Pressure Analysis for a Nitrogen-water Injection Well in Tahe Oilfield

HUXiaohua1WUFeng1LIYilong1YANGQiang1YAOZhuocheng2

(1. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University,Chengdu 610500, China; 2. Changqing General Drilling Company, CCDC, Xi′an 710018, China)

Abstract:The calculation of wellbore pressure of nitrogen-water injection is usually considered as a single phase. This paper developed a wellbore pressure analysis model for all situations of different ratio. This model separated the gas and water phase and considered the interface effect of two phases. Boundary conditions were given based on the interaction of reservoir pressure and bottom hole pressure. In the end, it solved the wellbore pressure by programming, by comparing the calculated and measured values, and the relative error was within 3.56%, the average is 1.71%, which were in the reasonable range.

Key words:Tahe oilfield; gas-liquid mixture; wellbore pressure; interface effect

文献标识码：A

文章编号：1673-1980(2016)01-0046-04

中图分类号：TE357

作者简介：胡晓华(1989 — )，女，四川简阳人，西南石油大学在读硕士研究生，研究方向为油气藏渗流理论与数值模拟技术。

基金项目：高等学校博士学科点专项科研基金项目(20115121120002)；国家自然科学基金项目“三维大变化尺度缝洞型碳酸盐岩油藏流体流动规律及流-固耦合综合模拟研究”(51374181)

收稿日期：2015-04-24