粒子群算法惯性权重的自适应改进与研究

邵明臣　彭业飞　张维继　冯智鑫　张武湛

摘要：针对粒子群算法存在早熟和收敛较慢两种缺陷，首先对粒子群算法的越界方式进行了改进，由于惯性权重是标准粒子群优化算法中一个重要的参数，决定了当前粒子速度对后续粒子的影响程度，从而控制整个算法的性能。在研究现有的几种惯性权重改进策略的基础上，提出基于适应度自适应动态调节的惯性权重改进算法。通过仿真研究不同的惯性权重对算法的影响，发现改进的粒子群算法在每次种群进行迭代时，根据每个粒子的适应度值自适应地改变其惯性权重，动态调整每个粒子的活性，提高了算法的全局搜索能力和收敛能力，较好的改进了原算法存在的缺点。

关键词：粒子群；早熟；惯性权重；自适应；全局搜索

中图分类号：TP312 文献标识码：A 文章编号：1009-3044（2016）02-0196-04

Abstract：The Particle Swarm Optimization has some shortcomings such as premature and slow convergence. Firstly， Transboundary way of the Particle Swarm Optimization has been improve in the paper. The Inertia Weight is an important parameter within the Particle Swarm Optimization.It determine the influence level which current particle against to the subsequent particle， so that it can controll the performance of the algorithm. The Fitness Adaptation Particle Swarm Optimization has been put forward based on researching several existing Inertia Weight improvement strategies. The simulation has been taken through comparing different inertia weight influence of the algorithm. Each particle adaptively change their inertia weight and dynamic adjustment active in each iteration. The Fitness Adaptation Particle Swarm Optimization improve the algorithm's global search ability and convergence capability. Simultaneously， it also improve the shortcomings of the original algorithm exists.

Key words： particle swarm； premature； inertia weight； adaptive； global search

1 概述

作为一种随机搜索算法，PSO算法主要存在着“早熟”和收敛较慢两个缺陷。为了避免“早熟”，许多研究者提出了通过控制种群多样性来提高算法性能的方法。Krink等学者通过解决粒子间的冲突和聚集[1]，基于种群随机多代初始化[2]等思想，给出了增强种群多样性的不同方法，使算法不会过早陷入局部极值；闫元元[3]等学者通过引入遗传算法的“交叉”和“变异”操作来增强全局搜索性能。虽然这些研究工作已经给出了提高PSO全局搜索能力的方法，但是它们很难既提高搜索速度又保持种群多样性。

粒子群优化算法的粒子在迭代过程中一直不断地向最优方向飞行，如果遇到局部极值点，所有粒子的速度很快降为零，导致粒子停滞不动，出现早熟收敛现象，且难以跳出局部极值点。针对这一缺点，出现了很多基本粒子群优化算法的改进算法。惯性权重是粒子群算法中非常重要的一个参数，是微粒群局部搜索和全局搜索能力的平衡点。惯性权重的选取对算法的优化效果具有较大影响。基于此，本文通过介绍现有的几种惯性权重改进策略，建立自适应动态调节策略的惯性权重改进算法，并进行仿真测试分析。

2 粒子群算法的越界处理

PSO算法基本思想可以描述如下：

3 现有的惯性权重值改进算法

惯性权重（）是标准粒子群优化算法中一个重要的参数，决定了当前粒子速度对后续粒子的影响程度，从而控制整个算法的性能。具有较强的探索能力的粒子继承较多，速度较大；具有较强的开发能力的粒子继承较小，速度较小。

3.1 线性递减权值策略（LAPSO）

线性递减权值（[LDW]）策略（Line Adaptation Particle Swarm Optimization，LAPSO）是由shi[4]等学者在1998年的进化计算的国际会议上提出的。惯性权重[ω]是用来控制粒子以前速度对当前速度的影响，进而影响粒子的全局和局部搜索能力。开始Shi只是将[ω]设为常数，通过实验统计发现，采用动态的[ω]比固定值更能够获得好的寻优结果。当[ω]较小，可以提高算法的局部细致寻优能力，而[ω]较大，可以提升算法收敛速度，所以通过调节[ω]可以取得收敛速度和局部寻优能力间的平衡。在PSO算法运算中，[ω]不仅可以线性变化，也可根据某个测度函数动态改变。LDW策略为：

[ωmax]、 [ωmin]分别为最大和最小惯性权重，[t]为当前迭代步数，[T]为算法总的迭代次数，[ω]常在[0.4，0.9]之间变化，随着迭代步数的增加而减小，算法在早期具有较快的收敛速度，而后期又有较强的局部搜索能力，[ω]引入使PSO算法性能有了很大提高。

3.2 周期性随机扰动策略（RAPSO）

学者于来行[5]提出了具有周期性扰动的惯性权重改进策略（Rand Adaptation Particle Swarm Optimization，RAPSO）。该策略基本思想是构造一个非线性变化的公式，通过加入周期性的随机扰动策略，从而避免算法陷入局部极值的弱点。由于较大的惯性权重[ω]有利于跳出局部极值点，而较小的有利于提高搜索精度，因此，通过加入正弦函数和随机函数对惯性权重[ω]交互扰动，并分别设定约束系数，使其随机改变，并且具有周期性波动下降趋势。

4 自适应动态调节的惯性权重改进算法

如前所述，在粒子群算法中，惯性权重[ω]起到了一个平衡全局寻优能力和局部寻优能力的作用，选择恰当的[ω]是提高算法的寻优能力和收敛能力的关键，基于此，本文在前人的基础上，建立基于适应度自适应动态调节的粒子群算法（Fitness Adaptation Particle Swarm Optimization，FAPSO），根据种群适应度平均值来自适应的调整[ω]。为了，本文建立的自适应调整策略，充分发挥自适应操作的效能，不仅用到群体早熟收敛信息，还根据个体适应值的不同将群体分为3个子群，对各自群体采用不同的自适应操作，并根据粒子的平均适应度评价粒子的优劣。这样就使得群体始终保持惯性权重的多样性。具体算法步骤为：

%假设求解最大值问题

[Step 1] 计算种群粒子适应度值的平均值[Fmean]，将最优粒子适应度记为[fm]；

[Step 2] 取出适应度值大于[Fmean]的粒子，计算其平均适应度[favg]，将适应度值大于[favg]的粒子赋予[ωmax]；

[Step 3] 取出适应度值小于[Fmean]的粒子，计算其平均适应度[f′avg]，将适应度值小于[f′avg]的粒子[ωmin]；

[Step 4] 将处于[favg]和[f′avg]之间的粒子赋予随[favg]和[fm]线性变化的值（式2.4）。

式5中，[i=1，2，…m]（[m]为种群大小），[ωmax]、[ωmin]分别表示[ω]最初设定的最大值和最小值，[fi]表示第[i]粒子当前的目标函数值。该方法的惯性权重随着粒子的目标函数值而自动改变，若粒子的目标值区域一致或者趋于局部最优，增加惯性权重使之跳出局部进行全局最优搜索；若各粒子的目标值比较分散，减小惯性权重进行最优搜索。同时，对于目标函数值优于平均目标的粒子，减小惯性权重可以保护该粒子，反之对于差于平均目标值的粒子，对应的权重增大，使之向较好的搜索区域靠拢。

5 算法仿真测试

5.1 测试函数

为了测试算法的性能，选用国际上通用[CEC]提出的[benchmarch]测试函数。本文采用以下四个经典的测试函数：

Rosenbrock函数在[x1，x2…xn=1，1…1]时达到极小值0。Rosenbrock函数全局最优点位于一个狭长且平滑的山谷内，一般的优化算法很难辨别搜索方向，使得函数的最优解很难寻找。

本文所有算法的仿真平台：处理器：Intel（R）Core（TM）i5-4210U CPU @1.7GHz 2.4GHz；安装内存：4.00GB；Windows版本：Windows7旗舰版；系统类型：64位操作系统；仿真软件：MatLab2013a。

5.2 仿真结果与分析

为了测试算法的性能，本文选取Griewank和Rastrigrin函数将LAPSO、RAPSO、FAPSO三种算法与BPSO算法（原始粒子群算法）进行仿真比较，参数设置为：迭代次数Gmax=500；种群规模m=20，学习因子C1=C2=2惯性权重[ω]最大值0.9，最小值0.4， 粒子最大速度设为粒子的范围宽度， BPSO算法的惯性权重为 0.64，越界处理方法均采用本文提出的随机初始化法。每种算法各运行 30 次并记录每次得到的全局极值，计算每种算法的可靠性和准确性并进行比较。

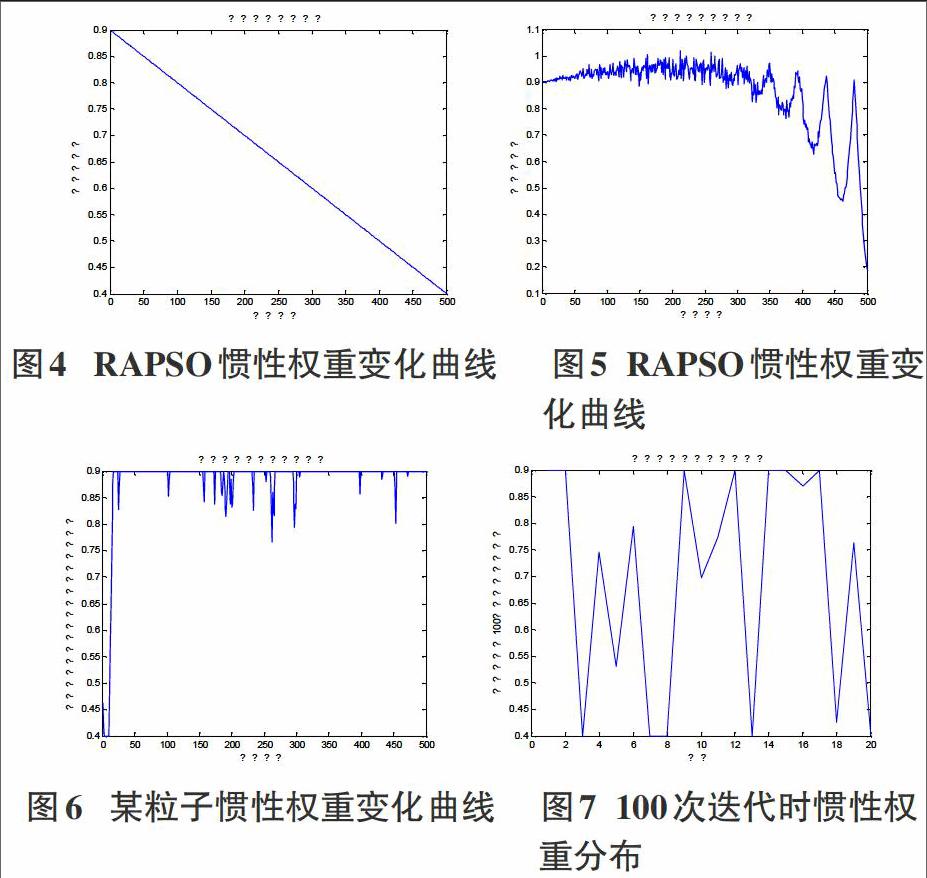
图4至图7分别给出了三种策略下惯性权重值的变化过程，其中，图4为随迭代次数线性变化的惯性权重，图5为周期性扰动的惯性权重变化曲线图，图6记录在FAPSO算法运行过程中某一粒子经历过的惯性权重值，图7给出了在FAPSO算法迭代100次时惯性权重在粒子中的分布图。

由图5可以看出，采用周期性随机扰动策略时，通过正弦函数和随机函数的交互扰动，惯性权重值随机改变并且具有周期性波动下降的趋势，开始时[ω]较大，随着迭代的进行，[ω]周期性波动下降。由图6和图7可以看出，基于适应度自适应调节[ω]的策略有这样的特点：同一粒子在不同的迭代次数具有不同的惯性权重，同一迭代次数各粒子的惯性权重不同。这种不同性是基于粒子本身的适应度实时进行调节的，很好地体现了“自适应”的思想。

由图8和图9可以看出，三种策略改进的惯性权重值均较好的提高了算法的寻优性能，尤其是基于适应度自适应调节的FAPSO算法，在搜索精度和收敛性上，更优于其他算法。

由以上数据可以看出，基于适应度动态调节的FAPSO算法，无论是从可靠性和准确性上比较，还是从最优解和方差（即算法的稳定性）上对比，FAPSO比LAPSO、RAPSO、BPSO有较大改进，同时，FAPSO算法对解决一些多峰函数等复杂问题也更胜一筹。

6 小结

本文首先对粒子群算法进行了越界改进，通过研究现有的几种惯性权重改进策略，提出采用基于适应度动态调节的惯性权重改进算法。改进的粒子群算法在每次种群进行迭代时，根据每个粒子的适应度值自适应地改变每个粒子的惯性权重，动态调整每个粒子的活性，提高了算法的全局搜索能力和收敛能力。总之，粒子群算法的惯性权重在粒子寻优过程中具有重要作用，如何寻找合适的惯性权重是提高算法性能关键。

参考文献：

[1] Krink T， Vesterstrom J S， Riget J. Particle swarm optimization with spatial particle extension. Pros. of the IEEE Int'1Conf.on Evolutionary Computation. Honolulu： IEEE Inc. 2002：1474-1497.

[2] Hu XH， Eberhart RC. Adaptive particle swarm optimization： Detection and response to dynamic system. Proc. of the IEEE Int'1 Conf. on Evolutionary Computation. Honolulu： IEEE Inc.， 2002：1666-1670.

[3] 闫元元，高兴宝，周喜虎. 基于变异和交叉的改进粒子群算法[J]. 陕西科技大学学报，2011（29）：121-124.

[4] Shi Y，Ebernart R.C...A modined partiele swam optimizer[C].Proeeedings of the IEE Congresson Evolutionary ComPutation，1998，69-73.

[5] 于来行，乔蕊.周期性扰动的微粒群算.计算机系统应用[J].2011， 20（ 6）：203-205.