基于有限元法计算三江平原地下水开发潜力研究

宫兴龙，付 强，李 衡，郭 佳(东北农业大学水利与建筑学院，哈尔滨 150030)

0 引 言

从20世纪90年代以后随着垦区兴起打井种稻,水稻的种植技术取得了长足的发展，产量稳步提高，同时由于打井大量开采地下水，降低了地下水位，涝渍碱危害减小。但人们担心,抽取的地下水水温低，影响着影响水稻米质与产量，在不断扩大水井稻的同时需要不断加大抽取地下水，导致地下水位不断下降，使这些地区可能面临超采，经济资源环境发展难可持续[1-3]。故本文仅重点论证地下水资源开发能否支撑本农场粮食生产、经济发展和生态环境可持续问题,即地下水资源开发潜力分析。很多人进行了三江平原地下水开发潜力研究，但大部分都是基于水量平衡法[4-9]，基于此本文尝试通过分析三江平原灌区典型区域853农场的水文地质条件，采用Galerkin法推导出该地区承压水的有限元方程组，并采用了改进平方根法求解该方程组，进而计算出853农场的地下水开发潜力。

1 地下水流数学模拟

承压水地下水运动采用的数学模拟模型如下[8]:

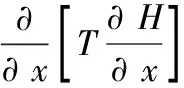
(1)

H(x,y,0)=H0(x,y)t=0,(x,y)∈Q

(2)

H(x,y,t)|Γ1=φ1(x,y)t=0,(x,y)∈Q

(3)

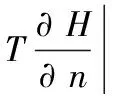
(4)

式中:T为导水系数；S为贮水系数；H0为水头初始值；φ1为Γ1(第一类边界)的已知水位函数；q为Γ2(第二类边界)上的侧向补给量；n为边界Γ1的外法线方向；Q为方程建立区域。

1.1 基于Galerkin法构建地下水运动有限元方程

对式(1)～式(4)采用Galerkin法得到有限元方程为：

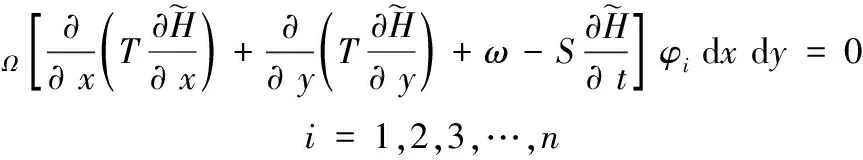
(5)

式中：φi为基函数；n为除了第一类边界上的节点外的节点数。

应用分布积分法(5)式得：

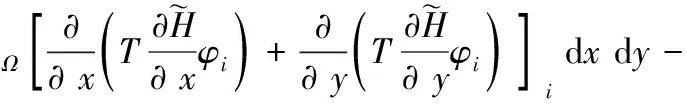
(6)

式(6)左端第一项应用Green公式:

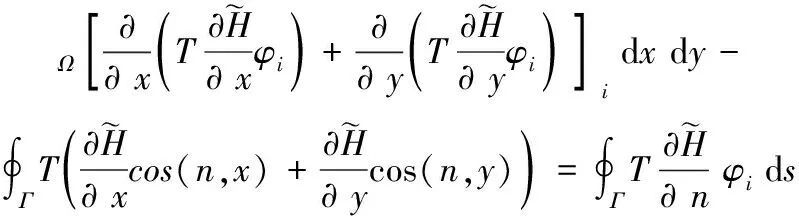
(7)

利用式(7)对式(6)整理：

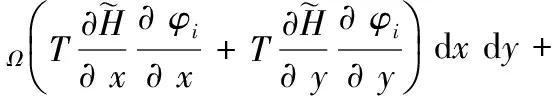
(8)

以三角元离散式(8)：

(9)

在单元上式(9)变形为：

(10)

式中:e表示三角单元上的变量。

1.2 有限元方程的构建

为了构建有限元方程对(10)变形为：

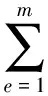
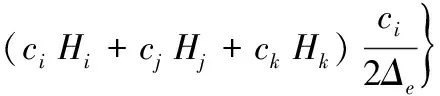
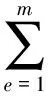
(11)

式中:Δe为三角元面积；qai,qik为边界段的流量；Lai,Li为边界段长度；a,b,c采用下式计算：

(12)

式中:(xi,yi)、(xj,yj)、(xk,yk)为三角元三个节点i,j,k的坐标。

1.3 方程组求解

式(12)利用矩阵形式为：

(13)

式中：导水系数矩阵D、贮水系数矩阵P、常数项矢量矩阵F。上述方程是具有对称，正定系数矩阵的线性方程，因此采用改进平方根法求解[9,10]。

1.4 抽水井有限元方程

“853”农场的取得地下水主要方式是利用抽水井进行抽水，如果抽水井在三角单元节点上应在三角单元方程(13)式上加一项：

(14)

式中：rwi为水井的半径。

如抽水井在单元的其他段，单位时间，单位面积上的垂直流出(入)含水层的量为ω=-Q/Fw(Fw单元面积)，单元e上的节点i,j,k依次有：

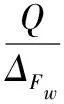
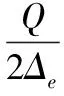
(15)

2 计算实例

2.1 研究区地质概况

853农场位于三江平原东部，宝清县境内，属于温暖半湿润农业气候区，多年平均降水量557.2 mm。在地理位置上，东南部紧靠完达山，西北及北部以平原河流挠力河为界，西南的以生产蛤蟆的蛤蟆通河为边界。本区有基岩裂隙孔隙含水层、第四系孔隙承压含水层、第三系裂隙承压含水层,第四系孔隙含水层系统在区内最重要，含水层较厚供水量充沛,从山前向河谷含水层逐渐增厚，地下水埋深逐渐变浅。第三系裂隙孔隙水系统内流动较弱，承压水的赋存、运输开采条件差于第四系，富水性差于第四系。该区农业灌溉用水主要来自于第四系含水层，该层地下水易于补给和排泄，因该区内地下水的开采还可能深入到第三系含水层,但开采量比较少，基于此本次模拟以第四系含水层为主。该区的主要补给方式是河流渗漏、降水入渗和侧向地下径流；人工抽水井开采是地下水排泄的主要方式,在开采量小的时间里还有一部分河流排泄和侧向径流排泄。

2.2 研究区域离散

为建立研究区的地下水流运动介质中的水文地质模型，基本步骤是要对实际水文地质条件加以概化，建立水文地质概念模型。根据上述水文地质特殊条件,本文主要致力于研究第四系含水层，山区第四系覆盖较薄，仅有少量孔隙裂隙潜水可供利用，其贮存于完达山麓，本次模拟不计。第三系裂隙孔隙承压水储存于巨厚的第四系含水层之下，在目前的开采条件和经济条件下尚难以对其进行开采，且收集资料困难，所以本次模拟也不考虑。由于第四系含水层其覆盖有10～35 m厚的亚黏土层,最厚达42 m，具有良好的隔水能力，地下水具有承压性质。故将含水层在垂向上概化为1层，即第四系孔隙承压含水层，其上腹亚黏土，下部为不透水基岩。水平三条河流概化为流量边界。采用有限元法数值求解式(7)对上述数学模型进行求解，对比例尺为1：10万的八五三农场综合水文地质图及地形图进行扫描，然后用数字化工具进行矢量化处理为栅格文件,将栅格文件导入River Tool工具，提取出挠力河，蛤蟆通河流，七里沁河和图1右下方的边界。模型作为计算模拟区的剖分底图计算区面积为1 182 km2，采用1 890个三角元进行离散见图1。图1上边的左边边线为挠力河，右边的线为七里沁河，下边的线为不透水边界，左下边的线为蛤蟆通河。

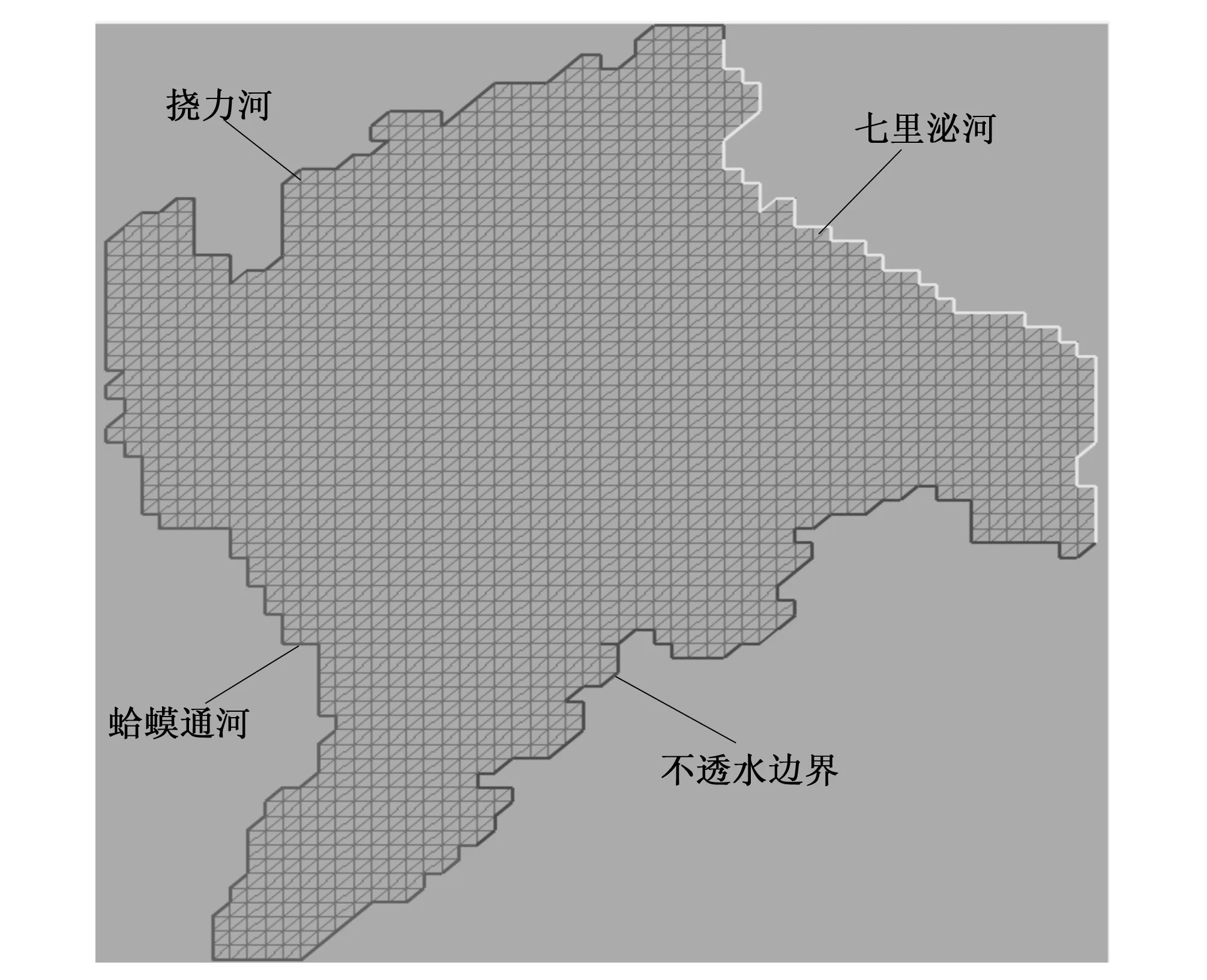
图1 853农场三角元离散图Fig.1 Discrete map of Triangular element in 853 farm

2.3 水位观测点

853农场有长期地下水观测井，本文选取7个长期观测井，分别为853农场1分场6小队的观井编号32号，2分场1小队的观井编号6号3分场7小队的观井编号10号，4农场1小队的观井编号25号，5农场2小队的观井编号20号，6农场5小队的观井编号14号，6农场9小队的观井编号13号。

2.4 降水量

降雨通过分析1995-2001年的月降水量数据，分析得到最大降水年份是1959年降水量为729.6m，多年平均降水量523.35。最小降水年份2004年458 mm。其过程线见图2。可见本地区降水量主要集中在6-8月份。本地区的降水入渗系数空间分布难于确定，因此本文根据清河灌区的设计值采用0.06。

图2 月降水量数据图Fig.2 Monthly rainfall data map

2.5 地下水开采控制水位判断

文献[4]还指出，根据水文地质条件，开采技术条件和社会生产需要，利用地下水变化直接反映开采程度的特点，提出合理的“地下水开采控制水位”概念，防止超量开采地下水导致地下水枯竭。笔者暂提出“理想水位(埋深)”概念，853农场承压开采为主区的理想水位本文控制在10～15 m。

2.6 目前开采条件下地下水开发程度

采地下水一直存在争议，本文以“853”农场的1998年到2012的观测井数据进行分析。以“853”农场的5农场2小队的观井编号20，因为其在清河灌区内，存在开采地下水进行水稻田灌溉的量大于其他各观测井所在的地区。从图可以看出地下水下降最大的一年是2012年，地下水为45.712 7 m。20号观测井的地面高程为58.912 7，其差值为13.5，由于其为承压区不超过15 m，因为本位认为853农场目前开采地下水不存在超采，而且还有一定开采的空间。由八五三农场五分场2队地下水位高程曲线图(图3)可以看出其地下水恢复地比较快，可见地下水很丰富,故有很大开发潜力。

图3 5分场2队地下水位高程曲线图Fig.3 The underground water level elevation curve in fifth parvial field second team

2.7 基于数值法推求地下水开发潜力研究

“853”农场从近年地下水动态分析，每年4月恢复水位埋深大约3.0 m，尚小于理想埋深最高值(10 m)。“853”农场属于以承压水为主的地下水开采由。挠力河河道宽广，一年时间里水深变化不大，在56.5 m波动，本文据此给出挠力河水位为56.5 m。蛤蟆通河水位较浅，本文采用的水位为河道高程，同理对于七里沁河也采用同样处理。对7个水位观测点的多年1月份的地下水水位分析得出其多年平均初始水位，采用距离倒数法插值得到计算所用的初始水位(见图4)。第四系承压含水层由于资料较少，其参数的选取主要是根据含水层水文地质特征,及前人的抽水试验,参照经验值给出初始值弹性释水系数0.003 5，导水系数1 560 m2/d。控制水位采用10～15 m。为了计算地下水开发潜力本例按照承压水理想埋深10～15 m计算地下水开发潜力，地下水为控制在水深10 m是计算的开发潜力为8 328.09万m3/a、地下水水位控制在15 m时，可得其开发潜力为9 456.09万m3/a。

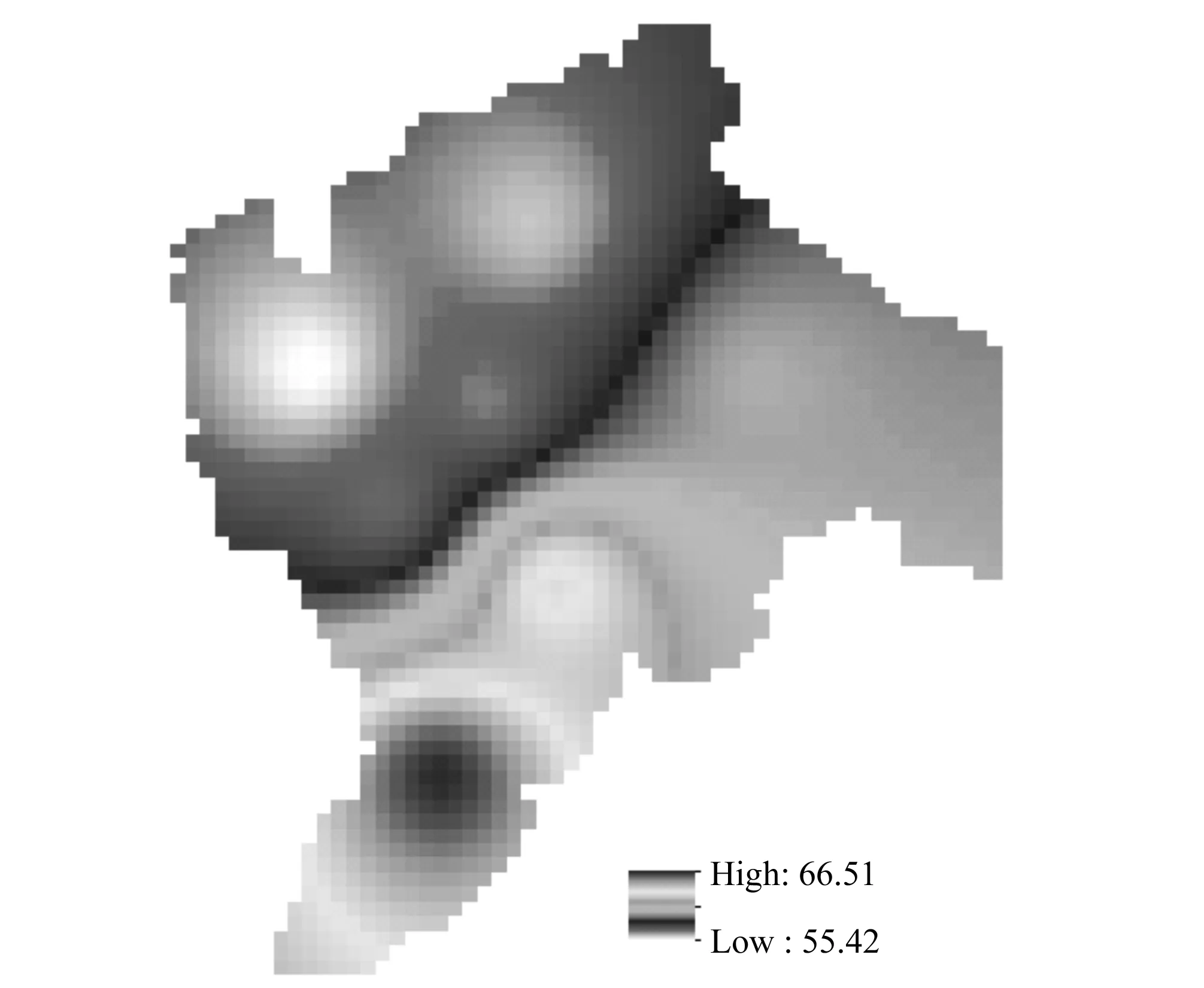
图4 853农场多年春季平均水位图Fig.4 The average water level diagram of spring for many years in 853 farm

2.8 激发出江河对地下水补给

“853”农场周围三面邻河，北及北部以挠力河为界，西南的蛤蟆通河，西北的挠力河，东北的越岭河，因此在控制开采地下水水位降到一定程度，就发生江河加大补给地下水[6]，基于此本位在控制承压区10～15 m，计算其激发的河流补给量。由于蛤蟆通河和七里沁河水位相对于承压水比较高，激发补给量不明显。因此本文的激发江河补给主要考虑挠力河，由计算可得，在控制降深水位取15 m，可得其激发的补给量为256.09 万m3/a。

3 结 语

综上所述，由“853”农场从1998-2013的观测井数据及地下水水位控制数据分析得出，目前“853”农场地下水开采不仅没有超采，而且还有很大开发潜力，地下水位下降只是7、8月份，之后随着地下水开采量减少，地下水水位迅速的恢复。由基于有限元法构建的地下水运动数值模型计算得到“853”农场可以开发9 456.09 万m3/a水量，“853”农场的北部靠近挠力河和西部的蛤蟆通的地区地下水开发量明显大于东部的靠近七里沁河的开采量。在合理控制地下水情况下，可以激发出江河更多的补给，挠力河中部补给量为256.09 万m3/a。

□

[1] 王立权,冯建维.水稻热的隐忧[J].水利天地,2004,(6):18-19.

[2] 张惠斌,于 东,姚章村.论“打井种稻”与“循环经济”[J].水利科技与经济,2006,12(12):820-821.

[3] 王立权,姚章村.高寒地区井灌水田井水增温技术的探索与实践[J].地下水,2006,28(3):46-49.

[4] 何 琏.中国三江平原[M].哈尔滨:黑龙江科学技术出版社,2000.

[5] 姚章村,安瑞强,董经财,等.三江平原建三江地下水激发补给初步分析[J].黑龙江水专学,2001,28(3):20-23.

[6] 李宏勋,陈 杰,李 伟,等.291农场地下水资源开发潜力初步分析[J].水利科技与经济,2008,14(1):49-51.

[7] 王贵玲,刘志明,刘花台,等.地下水潜力评价方法[J].水文地质工程地质,2003,(1):63-66.

[8] 薛禹群,谢春红.地下水数值模拟[M]. 北京：科学出版社,2007.

[9] 张德良.计算流体力学教程[M]. 北京：高等教育出版社,2009.

[10] 吴颂平,刘赵淼 译.计算流体力学基础及其应用[M]. 北京：高等教育出版社,2013.