改进的Fisher最优分割法在汛期分期中的应用

李 俊，武鹏林(太原理工大学水利科学与工程学院，太原 030024)

0 引 言

在汛期分期的基础上，制定各分期的汛限水位，以制定汛期内各个时期调度方案，使水库汛后的蓄满率得到提升，是实现洪水资源化的重要手段，更可以进一步使防洪与兴利相结合，增加水库的效益。

传统的汛期分期方法有数理统计法，模糊集合分析法等[1]，他们具有考虑因素单一、主观性强的缺点，而Fisher最优分割法在综合考虑多个因子的作用的同时又能保持样本的时序性，并能够确定最优分类数目[2],因此Fisher相对传统方法具有一定的优越性。考虑到各指标对样本的重要程度不同，把各个指标的权重通过主成分分析法计算出来，改进Fisher最优分割法，使其能够更加合理地考虑汛期分期的各个影响因子的重要程度，从而获得一个更加符合实际的分期结果。以吴城水库为例，本文使用该改进的方法对吴城水库汛期进行划分，并与模糊集合分析法[3]进行比较。

1 主成分分析法计算步骤

由于汛期分期是多指标的有序聚类分析，而各指标对样本分类的重要程度不同，因此首先采用主成分分析法计算各指标权重。

1.1 计算相关系数矩阵

构造样本阵X：

式中：xij为第i个样本中第j个指标的值。

对样本阵X做标准化，变为标准化阵Y：

由于汛期分期中各指标特征值为适度指标，因此采用下式对样本阵X进行标准化[4]：

(1)

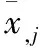
标准矩阵Y的相关系数矩阵的计算：

(2)

1.2 计算特征值与特征向量

1.3 计算主成分贡献率及累计贡献率

主成分Fi的贡献率为：

(3)

累计贡献率为：

(4)

当λk对应的累计贡献率大于或等于85%时，则其有k(k≤m)个与λ1,λ2,…,λk对应的主成分。

1.4 计算主成分载荷

主成分载荷反映主成分Fi和各指标之间的相关程度，各指标在各主成分Fi(i=1,2,…,k)上的载荷lij为：

(5)

通过(5)式得到lij，接着通过(6)式得到各主成分的线性模型：

Fi=e1iX1+e2iX2+…+emiXm(i=1,2,…,k)

(6)

这样，综合得分模型为[5]：

其中，ai反映了各指标变量在主成分中的综合重要度。

由此，得各指标变量的权重为：

(8)

2 Fisher最优分割法

Fisher最优分割法作为对有序时间样本序列进行聚类划分的方法，其分期依据是使样本总离差平方和最小，并以类内部差异最小，类间差异最大为原则。汛期分期属于聚类分析，而聚类分析又分为有序样本聚类分析与非有序样本聚类分析，Fisher最优分割法作为有序样本的聚类方法，其最优解是使分成各组总的离差平方和最小，而所有可能的分类中都保持了样本的时间连续性(换而言之，如果有一种分类破坏了样本的时间连续性，即使其总的离差平方和再小，这些组合在Fisher分割法中也是不予以考虑的)，正是这种特性使得Fisher最优分割法能够保持样本的时间连续性。

2.1 数据处理

在有序样本{X1，X2,…,Xn}中，每一个样本都对应m项指标，则可得以下矩阵X(xij为第i个样本的第j项指标的指标值)：

为了消除物理尺寸的影响，对数据进行以下转化：

(9)

式中：x′ij为标准化后的数量值；xmax,,j为第j列的最大值。

同时根据各个指标的权重，加权平均后得到向量Y，并以Y为基础数据进行汛期分期，Y可由下式求得：

(10)

2.2 定义类直径

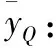
(11)

设D(i,j)表示Q的直径，则可以通过下式计算出D(i,j)：

(12)

2.3 定义目标函数

设将n个有序时间数据分为k类，则定义I(n，k)为其中一种分法，其可由下式进行计算：

(13)

根据Fisher分割法的划分原则，可得出当I(n，k)最小时对应的分法可以满足Fisher的划分原则，所以可以通过下式定义目标函数：

I*(n,k)=minI(n,k)

(14)

2.4 最优分割的推求过程

有以下定理：有序时间数据样本的最优k类分割，必须由最佳的k-1类分割在其某一个截尾子部分添加一个类组成。

递推公式表达为：

k=2时，

(15)

k>2时，

(16)

如果要把有序时间序列分成k类，先找出分割点ik，使得由递推公式计算出的I*(n，k)最小，则{yik，yik+1，…，yn}为第k类，然后再找分割点ik-1，使得I*(ik-1，k-1)最小，则同样可得第k-1类，即{yik-1，yik-1+1，…，yik-1}，依照同样的方法可以找出所有最优分类点。

2.5 最优分段数k的确定

通常I*(ik，k)～k曲线的拐点处对应的k为最优分段数，即最优分类数，或者计算：

γ(k)=|I*(n,k)-I*(n,k-1)|

(17)

后与k绘制γ(k)～k曲线， 最大所对应的k也是最优分段数。

3 实例分析

吴城水库位于中阳县的东川河上，流域属半干旱地区，气候特征为：干旱少雨，气候寒冷，降雨集中于7-9月。多年平均降水量为472 mm，时间和空间上分配不均匀，各年雨量差异大，全年降水量的70%都来自汛期。

3.1 指标选取

本文的基本资料为吴城水库1955-2007年(2001-2005 年未测)48 a的逐日降雨资料。研究的时间域为既定的6-9月，以旬为基本单位，在吴城水库控制流域内，选取能体现汛期的暴雨洪水变化规律的4个影响因子：多年旬平均降雨量、多年旬平均最大3 d雨量、多年大雨天数(降雨大于25 mm为大雨)、多年旬平均Cv值。

3.2 指标权重的确定

为了消除各指标物理尺度的影响，因此根据式(1)对样本指标进行处理，然后用SPSS软件对标准化的样本数据进行主成分分析，经分析可得表1及表2。

由表1可知，主成分1和2特征累积方差贡献率达到85.756%，超过85%。因此，前两个主成分能反映各项指标的绝大部分信息。

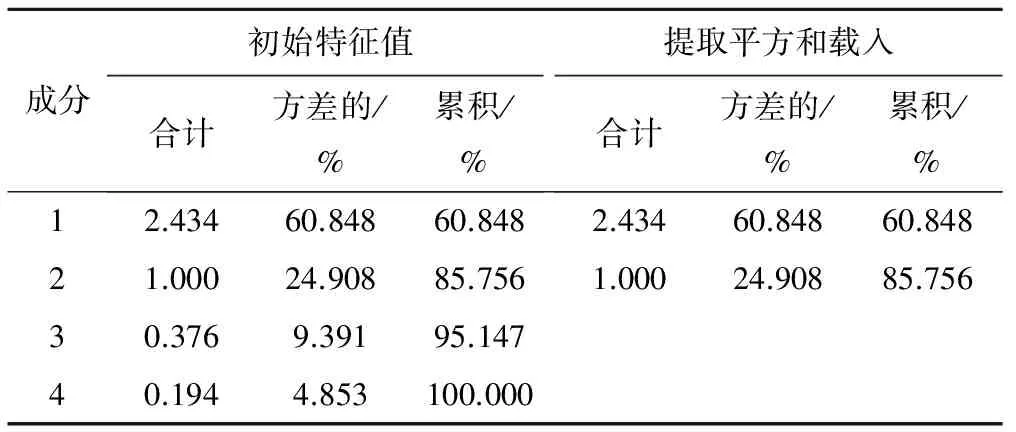
表1 解释的总方差Tab.1 Total variance explained

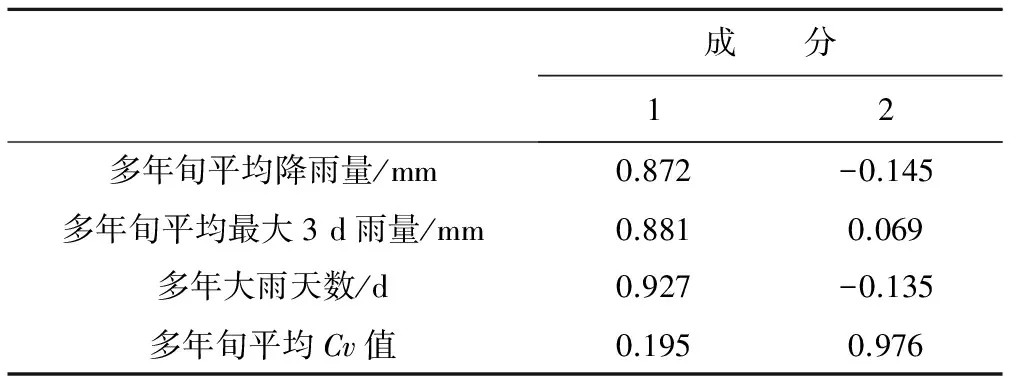
表2 成分矩阵Tab.2 Component matrix

根据式(5)可以得出样本各指标在主成分线性组合中的系数，再由(6)、(7)得到综合得分模型为：

F=0.373ω1+0.382ω2+0.421ω3+0.354ω4

(18)

根据式(8)求得各指标的权重为ω=(ω1,ω2,ω3,ω4)=(0.232,0.275,0.250,0.243)。

3.3 Fisher汛期分期

将求得的各指标权重系数代入式(10)，求得向量Y，由式(11)和式(12)计算各种组合的类直径，计算结果如表3所示。

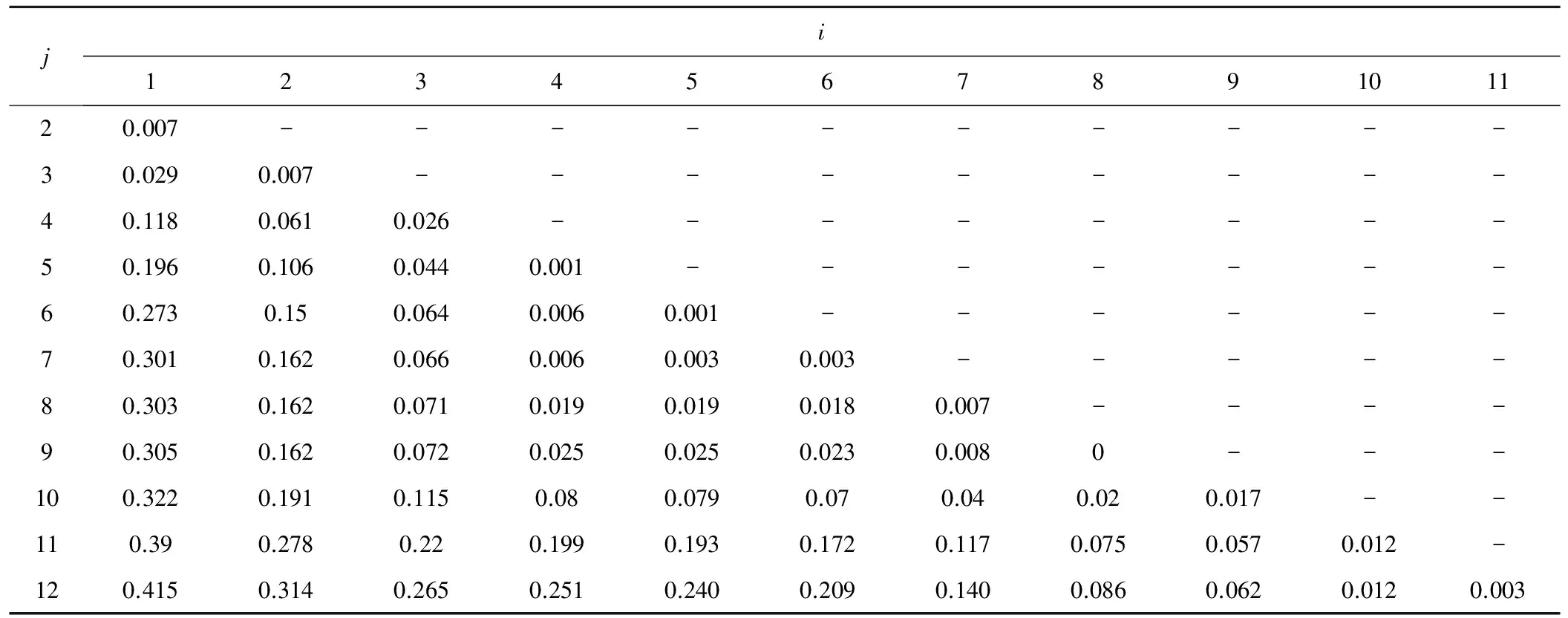
表3 各类分段直径D(i，j)Tab.3 The diameter of all kinds of section D(i，j)

目标函数I*(n,k) 通过式(15)和式(16)求得，计算结果见表4。

由式(17)计算出γ(k)，然后分别绘制I*(ik，k)～k、γ(k)～k曲线，分别见图1、图2。

由图1得，曲线在k=3处出现拐点，以此同时k=3时，γ(k)最大，所以分三类最优，由表4查得3个分类分别为1-3月,4-9月,10-12月，即6月1日-6月30日为前汛期，7月1日-8月31日为主汛期，9月1号-9月30日为后汛期。

4 成果分析

4.1 基于模糊集合分析法的汛期分期

本文采用模糊集合分析法[6]对吴城水库的汛期进行模糊分析，同时算出吴城水库汛期模糊集合的隶属度，见表5。

如果以隶属度大于0.5对应的时间作为汛期的话，由表5

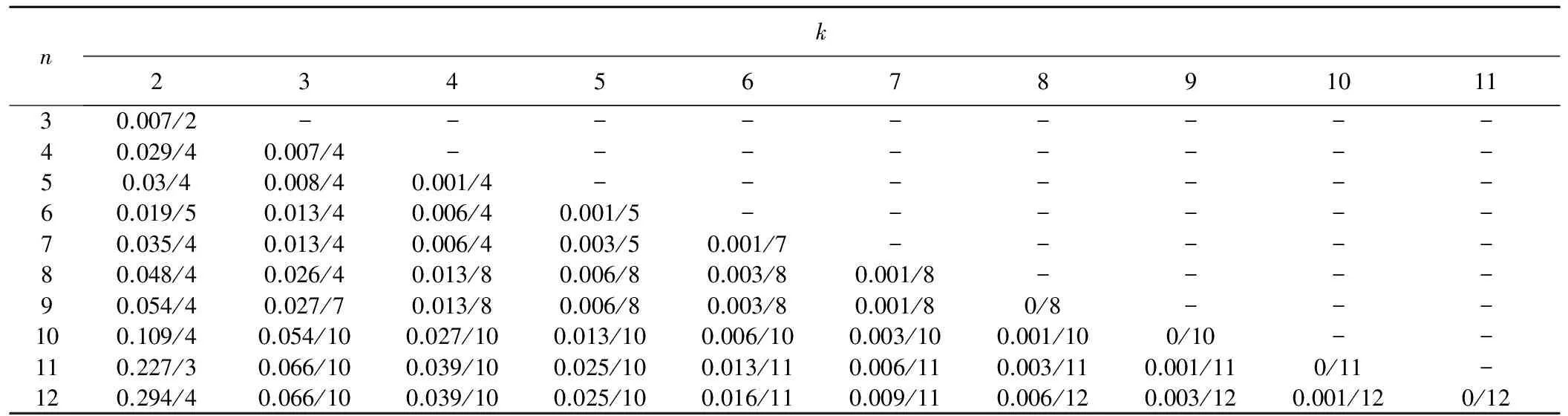
表4 分类目标函数I*(n, k)计算结果Tab.4 The calculation results of objective function I*(n, k)

注：斜线后的数字为当前分类情况下，第k类的与第k-1类的分割点ik。

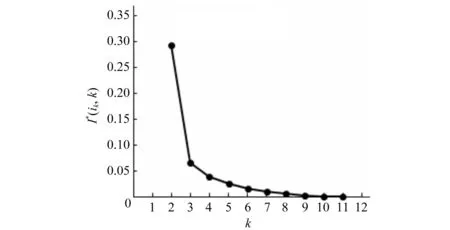
图1 I*(ik,k)～k关系图Fig.1 The relation between I*(ik,k) and k

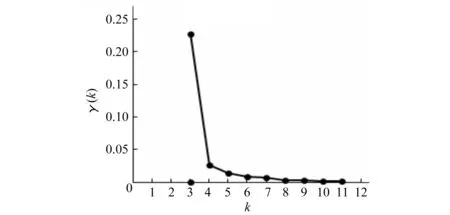
图2 γ(k)～(k)关系图Fig.2 The relation between γ(k) and k

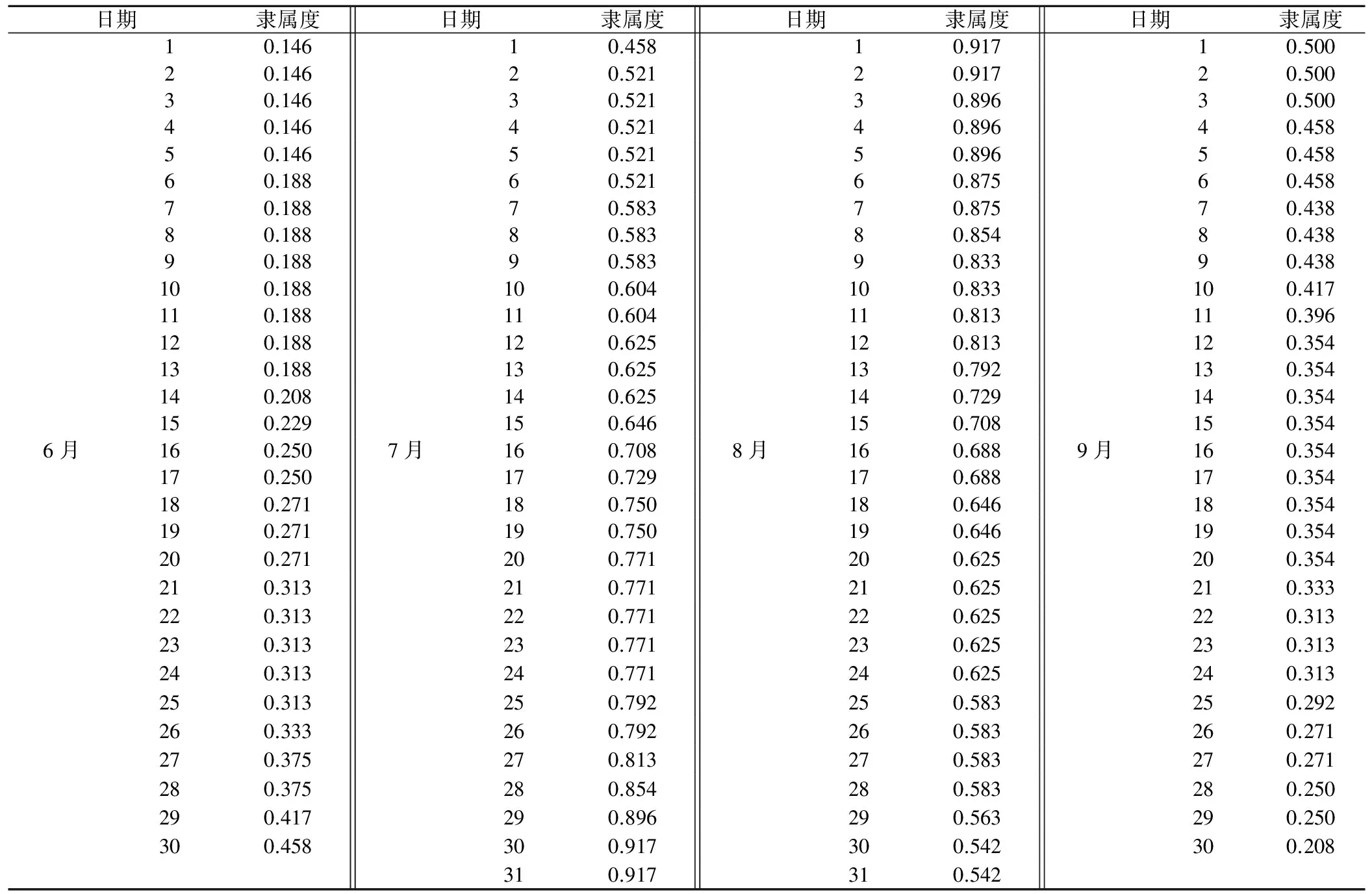
表5 吴城水库汛期经验隶属度Tab.5 Flood experience membership of Wucheng Reservoir

可以得到以下分期结果：

前汛期：6月1日至7月1日；主汛期：7月2日至9月3日；后汛期：9月4日至9月30日。为了便于比较把两种方法的分期结果见表6。

表6 结果比较表Tab.6 Results of comparison

4.2 两种结果比较

从以上的分析可以看出两种方法的划分结果一致，都能很好地反映出吴城水库的暴雨洪水变化特点。但是模糊集合分析法在阈值选取方面多数依靠经验选取，主观性强，相对而言Fisher最优分割法比较客观，因此说明了Fisher最优分割法可信，符合实际。

5 结 语

为了克服以往把各指标的权重看作相等的不足，本文利用主成分分析法计算各项指标权重以改进Fisher最优分割法，利用该改进的Fisher最优分割法对吴城水库控制流域进行汛期分期，并与模糊集合分析法的结果进行比较。通过分析我们发现，Fisher最优分割法适用于汛期分期，能使分期结果更加符合实际。

本文也存在很多不足：本文以旬为单位进行划分会人为打断水文的连续性，如果能使划分单位小一些，则可以使划分结果更加接近实际。由于资料有限，所以有一些指标也没能收集到，如能收集到逐日径流资料，则可以拥有更多关于吴城水库的暴雨洪水变化特点的信息，使分期更加科学。

□

[1] 喻 婷，郭生练，刘 攀，等. 水库汛期分期方法研究及其应用[J].中国农村水利水电，2006，(8)：24-26, 56.

[2] 刘克琳，王银堂，胡四一，等. Fisher最优分割法在汛期分期中的应用[J].水利水电科技进展，2007，27(3)：14-16, 37.

[3] 陈守煜. 工程水文水资源系统模糊集分析理论与实践[M]. 辽宁大连：大连理工大学出版社，1998..

[4] 焦立新. 评价指标标准化处理方法的探讨[J]. 安徽农业技术师范学院学报，1999，13(3)：7-10.

[5] 韩小孩，张耀辉，孙福军，等. 基于主成分分析的指标权重确定方法[J].四川兵工学报，2012，33(10)：124-126.

[6] 孙等平. 吴城水库汛期分期调度研究与应用[J].水利水电技术，2012，43(7)：109-112.